Advances in Remote Sensing
Vol.2 No.2(2013), Article ID:32875,7 pages DOI:10.4236/ars.2013.22016
Analysis of a Residual Model for the Decomposition of Polarimetric SAR Data
School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu, China
Email: *binbinhe@uestc.edu.cn, 449196341@qq.com, 452672784@qq.com
Copyright © 2013 Xiaojing Bai et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 19, 2013; revised March 22, 2013; accepted March 30, 2013
Keywords: Freeman-Durden Decomposition; Polarimetric SAR; Residual Model; Negative Scattering Energy
ABSTRACT
Accurate estimation of the double-bounce scattering fd and surface scattering fs coefficients with Freeman-Durden decomposition is still difficult. This difficulty arises because overestimation of the volume scattering energy contribution Pv leads to negative values for fd and fs. A generalized residual model is introduced to estimate fd and fs. The relationship between Pv and the residual model is analyzed. Eigenvalues computed from the residual model must be positive to explain physical scattering mechanisms. The authors employ a new volumetric scattering model to minimize Pv as calculated by several decomposition methods. It is concluded that decreasing Pv can help reduce negative energy. This conclusion is validated using actual polarimetric SAR data.
1. Introduction
Among the incoherent target decompositions for polarimetric SAR (PolSAR) data, Freeman-Durden decomposition (FDD), which is based on a physical model, consists of three types of scattering mechanisms: volumetric scattering, double-bounce scattering, and surface scattering [1]. FDD has been used for PolSAR data processing, such as speckle filtering [2], image classification [3] and soil moisture estimation [4].
However, there are three concerns about FDD model: the assumption of reflection symmetry in the azimuth, the elimination of the negative scattering power contribution from 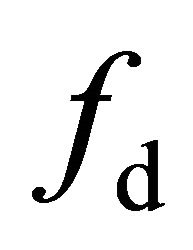 and
and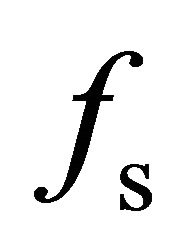 , and the selection of an appropriate volumetric scattering model
, and the selection of an appropriate volumetric scattering model . In urban settings, azimuthally symmetric reflection occurs inferquently. To remove the assumption that the reflection is symmetric, a helix was added as the fourth scattering component in Yamaguchi decomposition (YD), and similar terms (volumetric scattering, double-bounce scattering, and surface scattering) were used to those in the FDD model [5].
. In urban settings, azimuthally symmetric reflection occurs inferquently. To remove the assumption that the reflection is symmetric, a helix was added as the fourth scattering component in Yamaguchi decomposition (YD), and similar terms (volumetric scattering, double-bounce scattering, and surface scattering) were used to those in the FDD model [5].
A hybrid decomposition method was proposed by van Zyl et al. to overcome negative scattering energy [6]. Orientation angle compensation was employed by An et al. [7] and Lee and Ainsworth [8] to eliminate the negative scattering energy contribution. Subsequently, an adaptive model-based decomposition was proposed, which extended the method proposed by van Zyl et al. [9]. A hybrid Freeman/eigenvalues technique was used by Cloude for avoiding negative power problems [10]. Considering actual tree trunk and branch distribution, Yamaguchi et al. slightly modified the dipole model used in FDD model [5]. A unit matrix adopted as the new volumetric scattering model was introduced into the FDD method (abbreviated as UmFDD), and the major advantage of this new model was that it characterized the total randomness that was the prime feature of volume scattering [7].
In this paper, the authors attempt to adopt a new volumetric scattering model to minimize volume scattering energy for eliminating negative coefficients of doublebounce and surface scattering. Firstly, the authors review three decomposition methods: FDD, YD, and UmFDD. A generalized residual model is introduced to link these methods. Then, the authors analyze the relationship between the volume scattering energy contribution  and the residual model. The eigenvalues are extracted to analyze whether the generalized residual model can be used to interpret physical scattering mechanisms. The volume scattering contribution
and the residual model. The eigenvalues are extracted to analyze whether the generalized residual model can be used to interpret physical scattering mechanisms. The volume scattering contribution  is minimized by means of a new model, which confirms that decreasing the volumetric scattering contribution
is minimized by means of a new model, which confirms that decreasing the volumetric scattering contribution  can help reduce negative energy and gives the residual model an ability to explain physical scattering mechanisms.
can help reduce negative energy and gives the residual model an ability to explain physical scattering mechanisms.
2. Residual Model Extraction from Model-Based Decomposition
2.1. Residual Model Extracted from FDD Method
When the reciprocity assumption is valid for PolSAR imagery, each pixel of the image can be represented by a 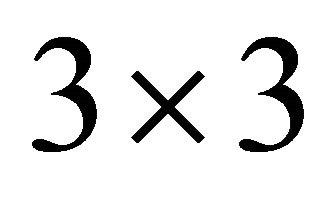 covariance matrix
covariance matrix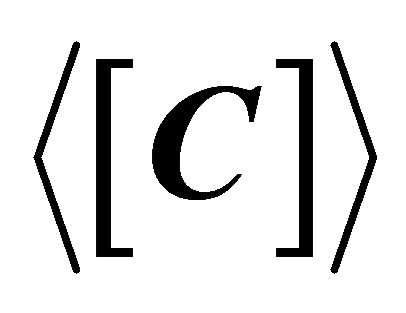 ,
,
 (1)
(1)
where  denotes a conjugate operator and
denotes a conjugate operator and 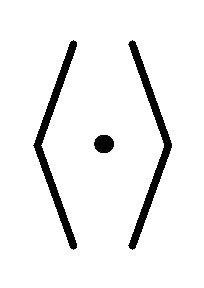 an assembled average.
an assembled average.  is a positive semi-definite Hermitian matrix.
is a positive semi-definite Hermitian matrix.
When a target is azimuthally symmetric, the reflection can be considered to be symmetric, and thus, the crossproducts of coand cross-polarized returns are zero. Thus, (1) becomes,
 (2)
(2)
Freeman and Durden [1] decomposed the covariance matrix 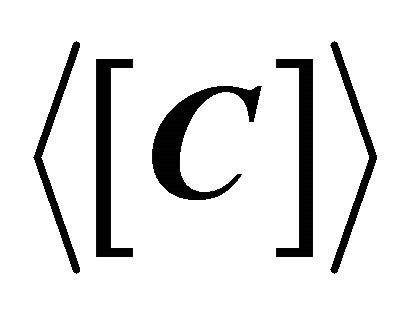 in (2) as the sum of three components representing scattering mechanisms of volumetric scattering
in (2) as the sum of three components representing scattering mechanisms of volumetric scattering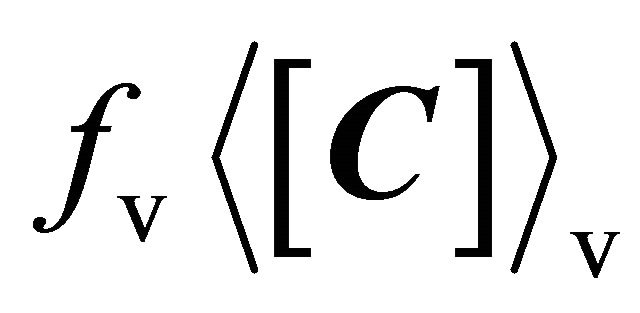 , double-bounce scattering
, double-bounce scattering , and surface scattering
, and surface scattering :
:
 (3)
(3)
where , and
, and 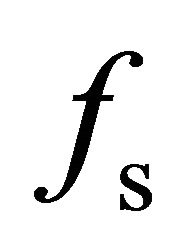 are scattering coefficients denoting the energy contribution for each scattering mechanism, respectively.
are scattering coefficients denoting the energy contribution for each scattering mechanism, respectively.
In FDD, the covariance matrix of the volumetric scattering component  is modeled as the scattering from a cloud of randomly oriented dipoles or long thin cylinders,
is modeled as the scattering from a cloud of randomly oriented dipoles or long thin cylinders,
 (4)
(4)
 is modeled as the scattering from a dihedral corner reflector,
is modeled as the scattering from a dihedral corner reflector,
 (5)
(5)
and  is modeled as a first-order Bragg scattering,
is modeled as a first-order Bragg scattering,
 (6)
(6)
The coefficient  can be directly computed from (3) to be,
can be directly computed from (3) to be,
 (7)
(7)
Then, the energy contribution  corresponding to the volumetric scattering component is,
corresponding to the volumetric scattering component is,

Inserting (4)-(6) into (3), and using the expression of 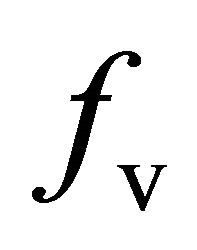 in (7) and
in (7) and  in (2), one can algebraically express the following equations:
in (2), one can algebraically express the following equations:
 (9)
(9)
(9) is the residual model derived from the FDD model. As shown in a previous study [11], the dominant scattering mechanism, that is, surface scattering or doublebounce scattering, can be determined by the sign of
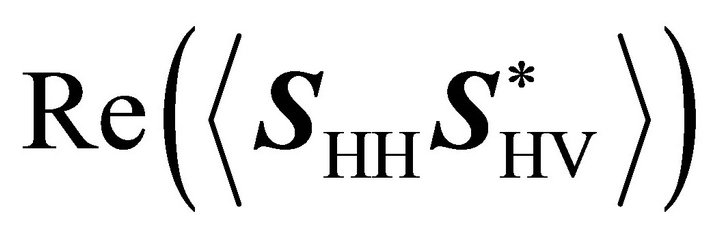 . When
. When , surface scattering dominates, and α = −1. When
, surface scattering dominates, and α = −1. When , the dominant mechanism is double-bounce scattering, and
, the dominant mechanism is double-bounce scattering, and . Therefore, with the determination of the dominant scattering component, there are only three unknowns in (9):
. Therefore, with the determination of the dominant scattering component, there are only three unknowns in (9): 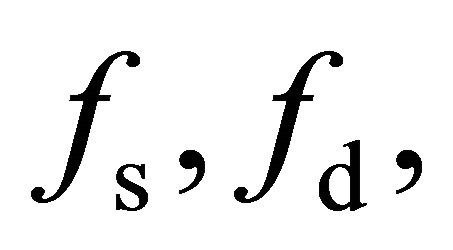 and
and 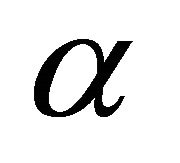 or
or . There are three independent equations in (9), so all unknowns can be solved.
. There are three independent equations in (9), so all unknowns can be solved.
2.2. Residual Model Extracted from YD Method
Considering the special case, azimuthally symmetric in urban areas, Yamaguchi et al. added a helix as the fourth component [5]. The covariance matrix for helix scattering 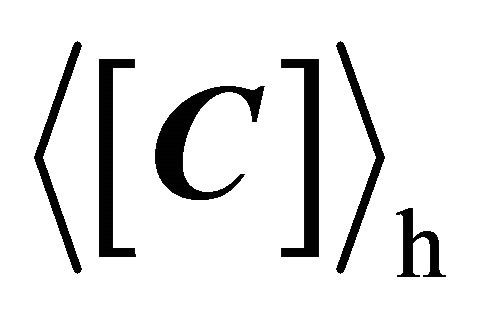 is,
is,
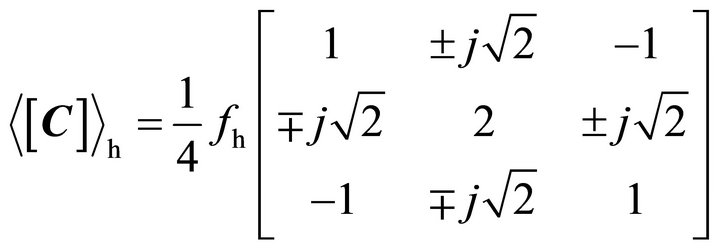 (10)
(10)
Then, the covariance matrix  of (1) is modeled as the sum of the four scattering components:
of (1) is modeled as the sum of the four scattering components:
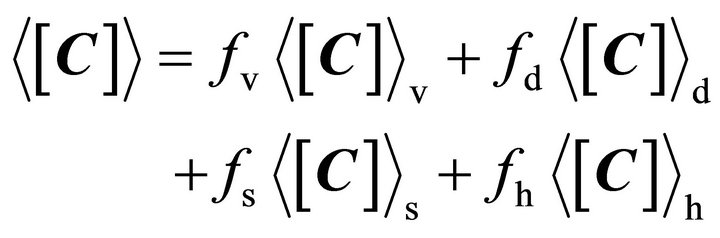 (11)
(11)
where  and
and 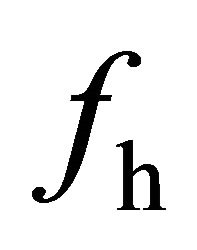 denote the scattering coefficients for each scattering mechanism, respectively.
denote the scattering coefficients for each scattering mechanism, respectively.
Yamaguchi et al. modified the volumetric scattering component [5] that was modeled as randomly distributed long thin cylinders [1] to reflect distribution patterns of tree trunks and branches. A general expression to represent the volume scattering model  is,
is,
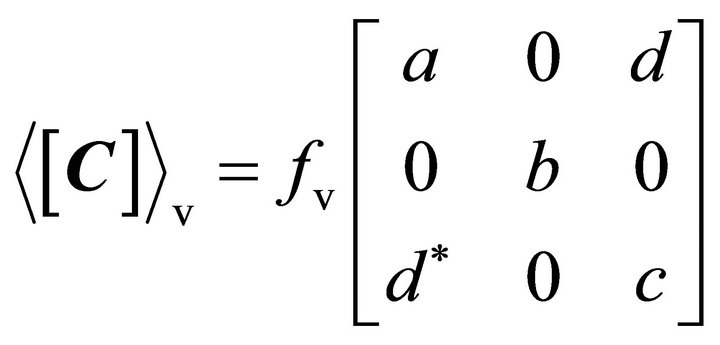 (12)
(12)
With the value of  as a thresholdthree sets of a-d are chosen to represent three volumetric scattering models. In the first model,
as a thresholdthree sets of a-d are chosen to represent three volumetric scattering models. In the first model,  , and a-d are sets such that
, and a-d are sets such that , and
, and
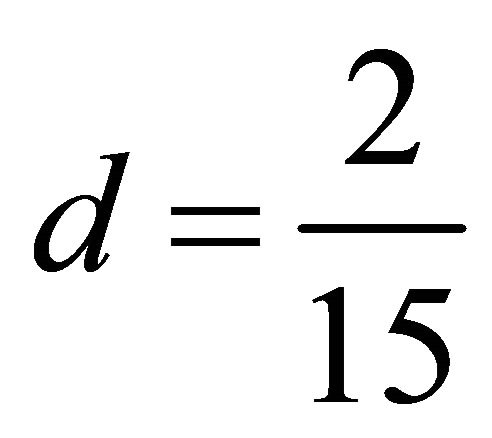 . In this case, the volumetric scattering is modeled as a cloud of horizontally oriented dipoles. When
. In this case, the volumetric scattering is modeled as a cloud of horizontally oriented dipoles. When
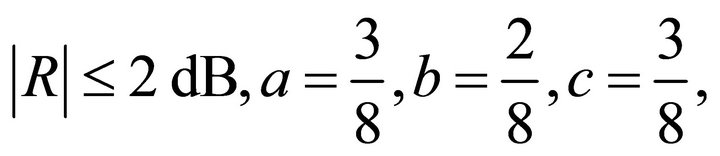 and
and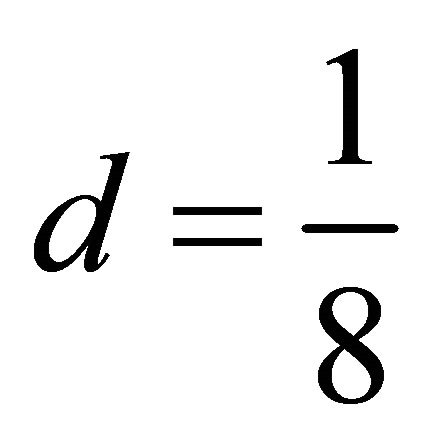 , and the covariance matrix of
, and the covariance matrix of  is the same as that in the FDD model. When
is the same as that in the FDD model. When  and
and
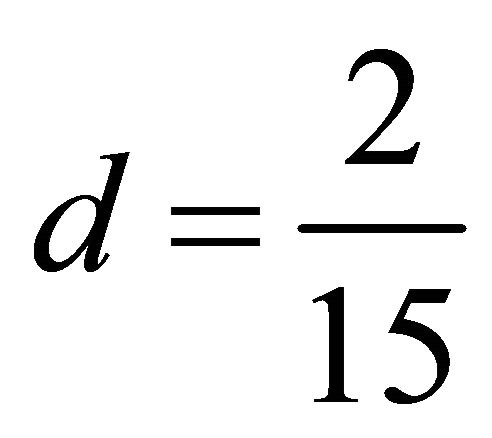 , and the volumetric scattering is modeled as a cloud of vertically oriented dipoles.In addition, the helix scattering coefficient
, and the volumetric scattering is modeled as a cloud of vertically oriented dipoles.In addition, the helix scattering coefficient 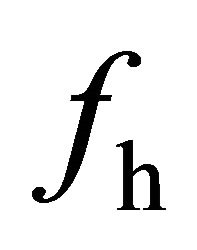 and the volume scattering coefficient
and the volume scattering coefficient 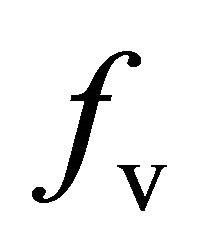 are directly computed from (11),
are directly computed from (11),
 (13)
(13)
The energy contribution  corresponds to the volumetric scattering such that,
corresponds to the volumetric scattering such that,
 (14)
(14)
Similar to the removal of 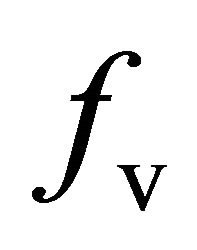 to obtain (9), and after the elimination of helix scattering and volumetric scattering related components, (11) can be expressed as:
to obtain (9), and after the elimination of helix scattering and volumetric scattering related components, (11) can be expressed as:
 (15)
(15)
Also equivalently to (9), (15) is the residual model extracted from the YD model. With a given
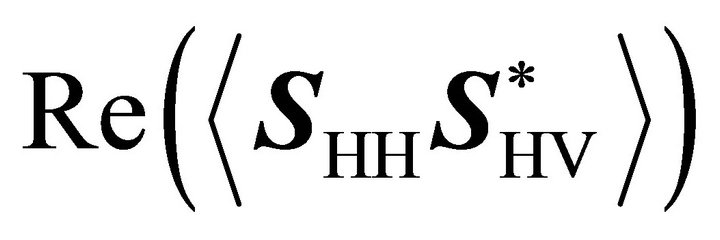 and
and  and
and 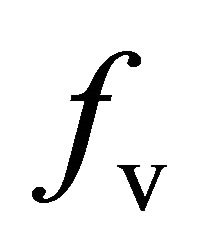 derived from (13), the remaining unknown parameters
derived from (13), the remaining unknown parameters ,
, 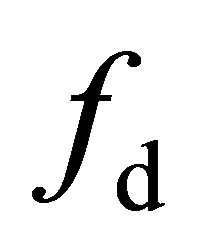 ,
, 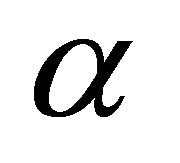 , and
, and  in (15) can be solved.
in (15) can be solved.
2.3. Residual Model Extracted from UmFDD Method
Considering that the volumetric scattering mechanism has high polarimetric entropy , An et al. introduced a new model [7], the unit matrix, which corresponds to totally random scattering. The coherency matrix for the new volume scattering model
, An et al. introduced a new model [7], the unit matrix, which corresponds to totally random scattering. The coherency matrix for the new volume scattering model  is,
is,
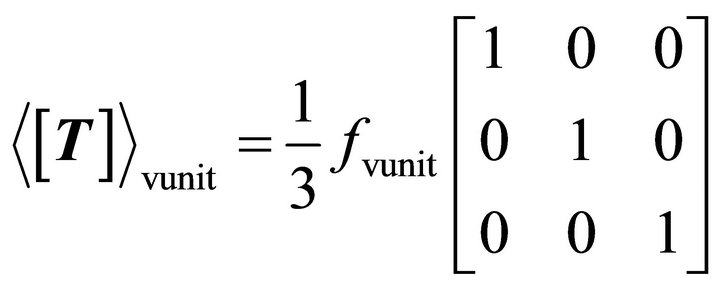 (16)
(16)
The correlation between the coherency matrix and the covariance matrix is,
 (17)
(17)
The new volumetric scattering model  is used to substitute for the original one in FDD [7], and the scattering coefficient
is used to substitute for the original one in FDD [7], and the scattering coefficient  is,
is,
 (18)
(18)
The scattering energy contribution  corresponding to this model is,
corresponding to this model is,
 (19)
(19)
The residual model extracted from UmFDD is:
 (20)
(20)
2.4. A Generalized Residual Model
Three of decomposition models: FDD, YD, and UmFDD, all can decompose the whole backscattering into three basic scattering mechanisms: volumetric scattering, double-bounce scattering and surface scattering. The differences are that the choice for the volume scattering model is different and the result for the volume scattering energy contribution is distinct. The volume scattering energy computed from FDD is the largest, YD followed by, and the value extracted from UmFDD is lowest.
After a close examination of (9), (15) and (20), one should note that the three residual models are structurally similar, with the double-bounce scattering and surface scattering related components on the right side of the equals sign in both equations. Symbolically, the right sides in (9), (15) and (20) are identical. Thus, a general expression can be used to represent them:
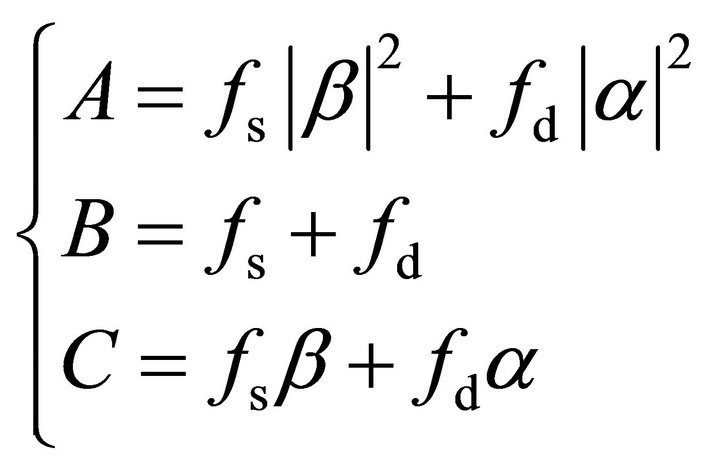 (21)
(21)
When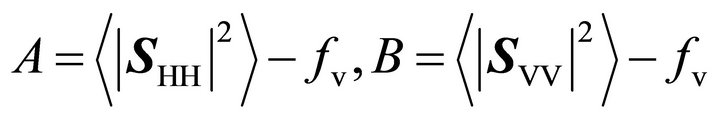 , and
, and
 , (21) is the residual model of (9).
, (21) is the residual model of (9).
When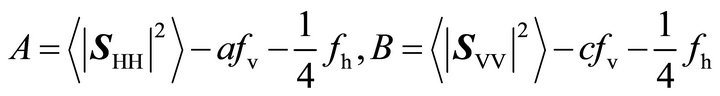 and
and , (21) becomes the residual model of (15). When
, (21) becomes the residual model of (15). When
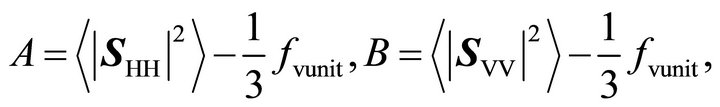 and
and
 , (21) becomes (20).
, (21) becomes (20).
3. Properties of the Generalized Residual Model
3.1. Relationship between Volumetric Scattering and Negative Energy
Because , and
, and 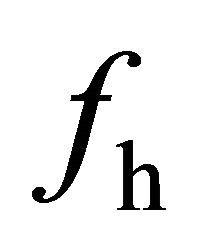 denote energy coefficients for different types of scattering mechanisms, they should all be positive, which is consistent with the actual physical scattering mechanisms observed in reality. Because surface scattering and double-bounce scattering have no contribution to cross-polarized return, the volume scattering coefficient
denote energy coefficients for different types of scattering mechanisms, they should all be positive, which is consistent with the actual physical scattering mechanisms observed in reality. Because surface scattering and double-bounce scattering have no contribution to cross-polarized return, the volume scattering coefficient 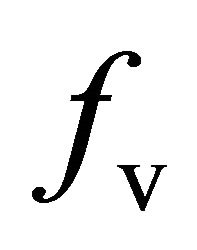 can be directly estimated from PolSAR data. The helix scattering coefficient
can be directly estimated from PolSAR data. The helix scattering coefficient 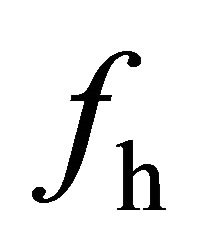 can be computed from (13) as well. Both
can be computed from (13) as well. Both 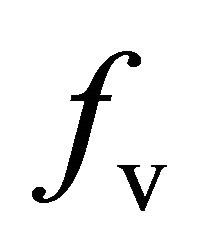 and
and  are positive, which can be seen from Equations (7), (13) and (18). The parameters
are positive, which can be seen from Equations (7), (13) and (18). The parameters 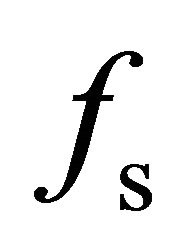 and
and 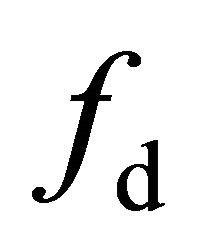 are computed from the data using the generalized residual model (21). The difficult and troublesome problems in (21) are that the scattering coefficients
are computed from the data using the generalized residual model (21). The difficult and troublesome problems in (21) are that the scattering coefficients  and
and  aresometimes negative, which is not consistent with the physical scattering mechanisms. Negative results for the coefficients
aresometimes negative, which is not consistent with the physical scattering mechanisms. Negative results for the coefficients  and
and 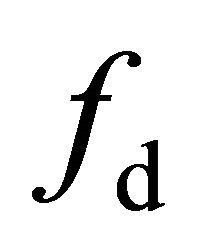 must be reduced or eliminated.
must be reduced or eliminated.
Comparing (8) and (14), the volume scattering contribution  computed from FDD is more overestimated than the ones extracted from the YD and UmFDD methods. In addition, the negative scattering coefficients
computed from FDD is more overestimated than the ones extracted from the YD and UmFDD methods. In addition, the negative scattering coefficients  and
and 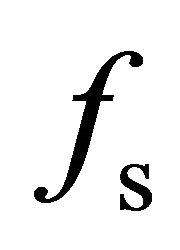 computed with YD and UmFDD are reduced compared with the results obtained from the FDD method. That is to say, the value for volume scattering energy contribution
computed with YD and UmFDD are reduced compared with the results obtained from the FDD method. That is to say, the value for volume scattering energy contribution  is strongly related to the scattering component coefficients
is strongly related to the scattering component coefficients  and
and . We can reduce the negative coefficients
. We can reduce the negative coefficients 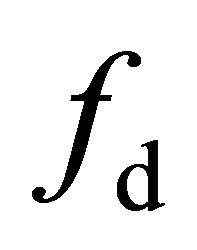 and
and 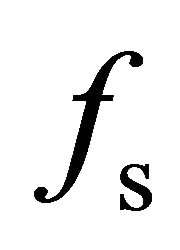 by decreasing the volume scattering energy contribution
by decreasing the volume scattering energy contribution . The following experiments will be used to validate that the emergence of negative values for the scattering mechanisms
. The following experiments will be used to validate that the emergence of negative values for the scattering mechanisms  and
and 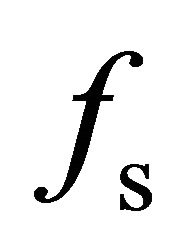 should be attributed to the overestimation of the volume scattering contribution
should be attributed to the overestimation of the volume scattering contribution 
3.2. Eigenvalues of the Generalized Residual Model
Based on the work of van Zyl et al. [12], the covariance matrix 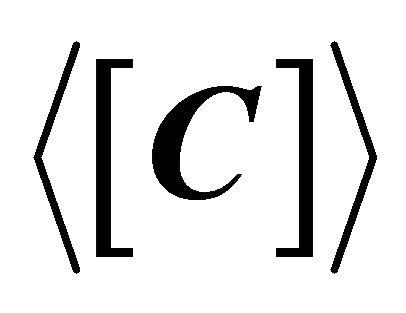 is expressed as the sum of a determined scattering model
is expressed as the sum of a determined scattering model  and a residual model
and a residual model 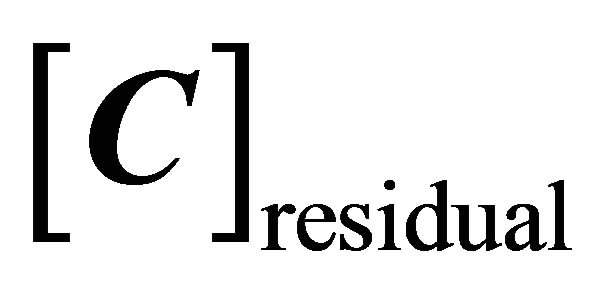 , which has the same meaning as (21) but with a different formulation:
, which has the same meaning as (21) but with a different formulation:
 (22)
(22)
where a is constant. In this paper, we set , so (22) can be rewritten as:
, so (22) can be rewritten as:
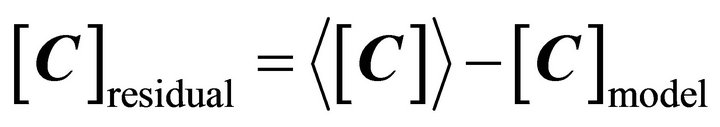 (23)
(23)
The residual model (23) can be expressed as,
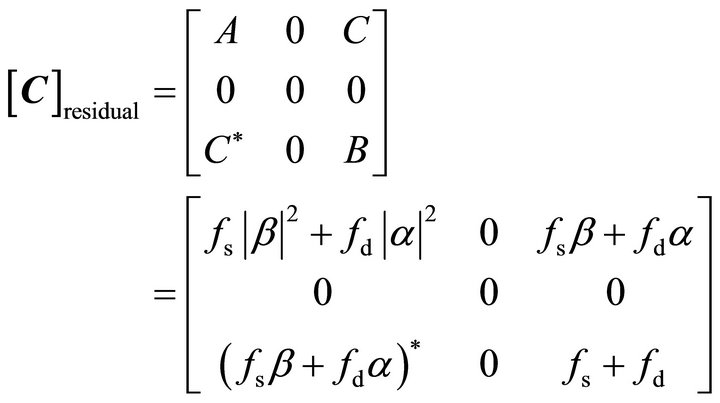 (24)
(24)
The variables A, B, and C in (24) have the same meaning as those in (21). Because the right-hand side of (24) represents physical scattering mechanisms, the eigenvalues computed from (24) must be positive [12]. Only positive eigenvalues correspond to actual physical scattering mechanisms, which has been discussed in the work of van Zyl et al. [12]. Because volumetric scattering and helix scattering have been eliminated, there are at most two non-zero eigenvalues computed from (24). Both of the two eigenvalues should be positive, but this is not true. The following experiment is carried out to statistically count the percentage of negative eigenvalues computed from the residual model (24). It will show that the volumetric scattering contribution  has high correlation with the proportion of negative eigenvalues.
has high correlation with the proportion of negative eigenvalues.  should be reduced to ensure that the residual model is able to represent the physical scattering mechanisms.
should be reduced to ensure that the residual model is able to represent the physical scattering mechanisms.
3.3. Volumetric Scattering Model Minimization
In the previous section’s analysis, it was observed that an overestimated volumetric scattering contribution  will lead to negative coefficients
will lead to negative coefficients  and
and  and negative eigenvalues computed from the residual model (24). Thus, we try to minimize the volumetric scattering energy contribution
and negative eigenvalues computed from the residual model (24). Thus, we try to minimize the volumetric scattering energy contribution , so that the scattering coefficients
, so that the scattering coefficients 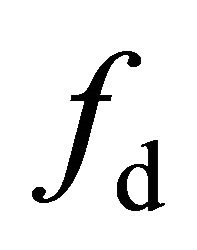 and
and  will be accurately estimated.
will be accurately estimated.
We assume that volumetric scattering only has no contribution to co-polarized returns but to cross-polarized return. The covariance matrix for volumetric scattering, as shown in (25), corresponds to the minimum scattering energy contribution,
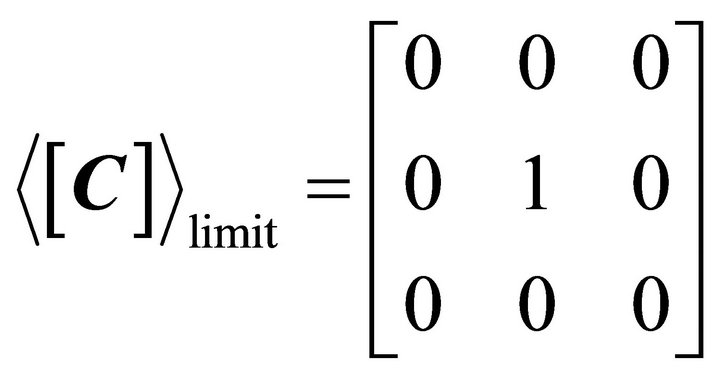 (25)
(25)
The corresponding volume scattering coefficient for the three decomposition models,
 (26)
(26)
The modified residual model is written here:
 (27)
(27)
When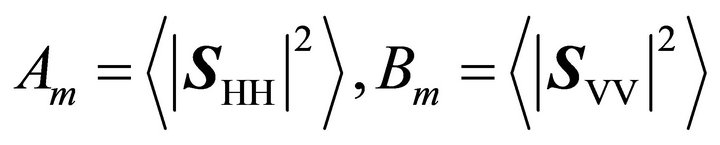 , and
, and
 , (27) is the modified residual model extracted from FDD and UmFDD model. When
, (27) is the modified residual model extracted from FDD and UmFDD model. When
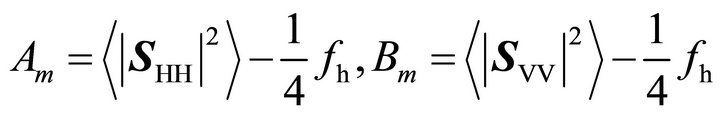 , and
, and
 , (27) becomes the modified residual model extracted from YD.
, (27) becomes the modified residual model extracted from YD.
From (26), we learn that the volumetric scattering contribution  has been minimized. When
has been minimized. When  reaches its minimum, the negative scattering coefficients
reaches its minimum, the negative scattering coefficients 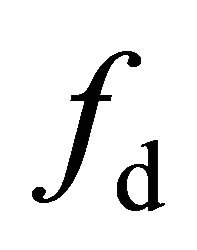 and
and  will be greatly reduced, and the negative eigenvalues computed from the residual model (27) will be decreased as well. This view will be validated in the following experiments.
will be greatly reduced, and the negative eigenvalues computed from the residual model (27) will be decreased as well. This view will be validated in the following experiments.
4. Experiment
The Advanced Land Observing Satellite (ALOS) L-band PolSAR dataset for San Francisco is used in this paper. The satellite image, including the ascending track, was acquired on 11 November 2009. The incidence angle is 22.74˚ in the near range and 24.95˚ in the far range. We chose a 512 × 512 sub-image for this experiment, and the sub-image is multilook processed in the azimuth direction.
First, the scattering component coefficients 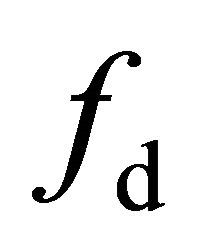 and
and  are computed from the residual model (21). The statistical proportion of negative values for
are computed from the residual model (21). The statistical proportion of negative values for  and
and  is given in Table 1.
is given in Table 1.
Some scattering coefficients  and
and  are negative. The percentage of negative values for
are negative. The percentage of negative values for  and
and  computed from FDD is higher than the ratios computed for the YD and UmFDD methods. The volume scattering energy contribution
computed from FDD is higher than the ratios computed for the YD and UmFDD methods. The volume scattering energy contribution  extracted from FDD is overestimated compared with YD and UmFDD. This observation confirms that the overestimation of the volumetric scattering contribution
extracted from FDD is overestimated compared with YD and UmFDD. This observation confirms that the overestimation of the volumetric scattering contribution will lead to negative energy.
will lead to negative energy.
Second, the statistical percentages of negative eigenvalues computed from the residual model (24) are displayed in Table 2, where  denotes a relatively large eigenvalue, and
denotes a relatively large eigenvalue, and 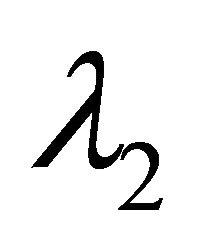 denotes a relatively small one.
denotes a relatively small one.
It can be seen from Table 2 that some eigenvalues  and
and 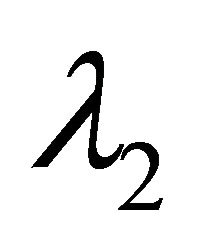 are negative. The YD and UmFDD methods perform better than FDD. The volume scattering model is strongly related to the residual model, as mentioned in the previous section. The residual model (24) represents physical scattering mechanisms. It is best to ensure that the eigenvalues computed from residual model (24) are positive. Only positive eigenvalues correspond to physical scattering mechanisms. The selection of an appropriate volumetric scattering model is a way to ensure positive eigenvalues.
are negative. The YD and UmFDD methods perform better than FDD. The volume scattering model is strongly related to the residual model, as mentioned in the previous section. The residual model (24) represents physical scattering mechanisms. It is best to ensure that the eigenvalues computed from residual model (24) are positive. Only positive eigenvalues correspond to physical scattering mechanisms. The selection of an appropriate volumetric scattering model is a way to ensure positive eigenvalues.
Finally, a new volumetric scattering model (27) is introduced to the FDD, YD, and UmFDD methods. The
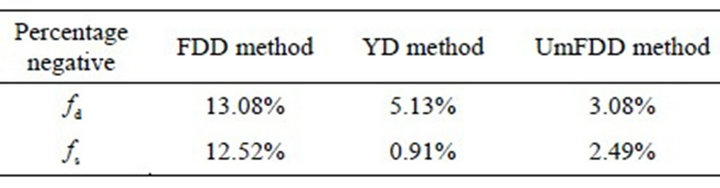
Table 1. Negative parameters 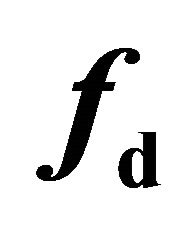 and
and  computed from (21).
computed from (21).
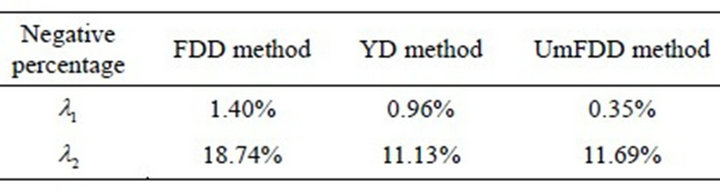
Table 2. Negative eigenvalues 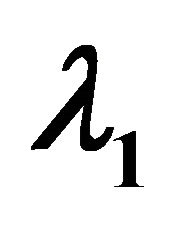 and
and  computed from (24).
computed from (24).
scattering coefficients  and
and 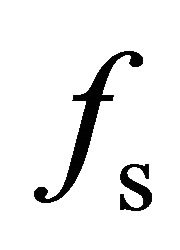 are computed from the residual model (27). Eigenvalues are extracted from (27) as well. The results are shown in Table 3.
are computed from the residual model (27). Eigenvalues are extracted from (27) as well. The results are shown in Table 3.
When the volume scattering energy contribution  is minimized, the scattering component coefficients
is minimized, the scattering component coefficients 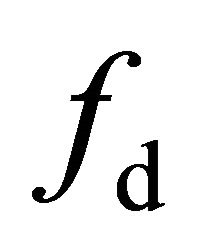 and
and  computed from the generalized residual model are almost all positive. The eigenvalues
computed from the generalized residual model are almost all positive. The eigenvalues 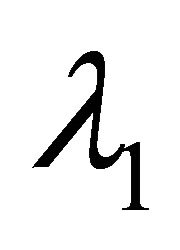 and
and 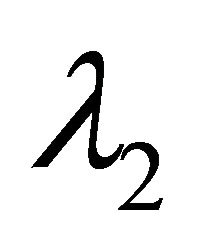 are almost being positive. This observation indicates that the residual model (27) is able to represent surface scattering and double-bounce scattering.
are almost being positive. This observation indicates that the residual model (27) is able to represent surface scattering and double-bounce scattering.
The new volumetric scattering model (25) is adopted under the assumption that volumetric scattering has no contribution to co-polarized returns but only to crosspolarized return, which is not consistent with physical scattering in reality. In this situation, the volume scattering energy contribution is less overestimated. We should keep a balance between the volumetric scattering energy contribution and the negative scattering coefficients  and
and 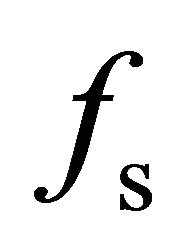 so that the volumetric scattering model can reflect the physical scattering mechanisms and the scattering coefficients
so that the volumetric scattering model can reflect the physical scattering mechanisms and the scattering coefficients  and
and  are accurately estimated.
are accurately estimated.
5. Conclusions
To reduce the negative scattering coefficients for doublebounce scattering  and surface scattering
and surface scattering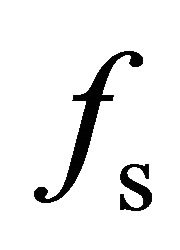 , a general residual model is introduced, which is extracted from FDD, YD, and UmFDD methods. There is a high correlation between volume scattering energy
, a general residual model is introduced, which is extracted from FDD, YD, and UmFDD methods. There is a high correlation between volume scattering energy  and scattering coefficients
and scattering coefficients  and
and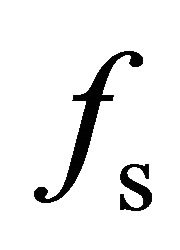 . When the value of
. When the value of  is greater, the more negative
is greater, the more negative  and
and  computed from the residual model.
computed from the residual model.
In this paper, the authors adopt a new volume scattering model to minimize . When
. When  reaches to its minimum, the percentage of negative parameters
reaches to its minimum, the percentage of negative parameters 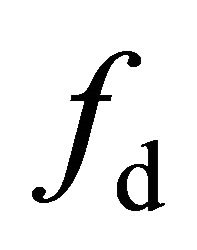 and
and 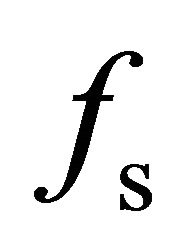 is greatly reduced, and the proportion of negative eigenvalue computed from residual model is rapidly decreased, which is validated using the actual PolSAR data. It is concluded that decreasing the volume scattering contribution
is greatly reduced, and the proportion of negative eigenvalue computed from residual model is rapidly decreased, which is validated using the actual PolSAR data. It is concluded that decreasing the volume scattering contribution can help to reduce the presence of negative values for the scattering coefficients
can help to reduce the presence of negative values for the scattering coefficients 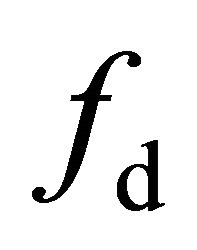 and
and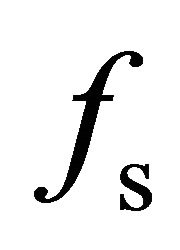 .
.
6. Acknowledgments
This work was supported by the Fundamental Research
Table 3. Negative parameters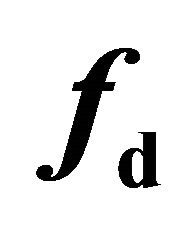 ,
, 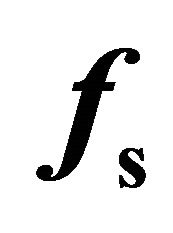 ,
,  and
and  computed from (27).
computed from (27).
Fund for the Central Universities (Contract # ZYGX- 2012Z005) and the National Natural Science Foundation of China (Contract #41171302). We express our gratitude to Dr. Yong Wang from East Carolina University for his instruction and advice.
REFERENCES
- A. Freeman and S. L. Durden, “A Three-Component Scattering Model for Polarimetric SAR Data,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 36, No. 3, 1998, pp. 963-973. doi:10.1109/36.673687
- J. S. Lee, M. R. Grunes, D. L. Schuler, E. Pottier and L. Ferro-Famil, “Scattering Model-Based Speckle Filtering of Polarimetric SAR Data,” IEEE Transactions on Geosciences and Remote Sensing, Vol. 44, No.1, 2006, pp. 176-187. doi:10.1109/TGRS.2005.859338
- J. S. Lee, M. R. Grunes, E. Pottier and L. Ferro-Famil, “Unsupervised Terrain Classification Preserving Polarimetric Scattering Characteristics,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 42, No. 4, 2004, pp. 722-731. doi:10.1109/TGRS.2003.819883
- I. Hajnsek, T. Jagdhuber, H. Schon and K. P. Papathanassiou, “Potential of Estimating Soil Moisture under Vegetation Cover by Means of PolSAR,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 47, No. 2, 2009, pp. 442-454. doi:10.1109/TGRS.2008.2009642
- Y. Yamaguchi, T. Moriyama, M. Ishido and H. Yamada, “Four-Component Scattering Model for Polarimetric SAR Image Decomposition,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 43, No. 8, 2005, pp.1699-1706. doi:10.1109/TGRS.2005.852084
- J. Jakob, J. J. Van Zyl and Y. Kim, “Requirements for Model-Based Polarimetric Decomposition,” Proceedings of IEEE International Geoscience and Remote Sensing Symposium 2008, Vancouver, 24-29 July 2011, pp. 417- 420.
- W. An, Y. Cui and J. Yang, “Three-Component ModelBased Decomposition for Polarimetric SAR Data,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 48, No. 6, 2010, pp. 2732-2739. doi:10.1109/TGRS.2010.2041242
- J. S. Lee and T. L. Ainsworth, “The Effect of Orientation Angle Compensation on Coherency Matrix and Polarimetric Target Decompositions,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 49, No. 1, 2011, pp. 53-64. doi:10.1109/TGRS.2010.2048333
- M. Arii, J. J. Van Zyl and Y. Kim, “Adaptive ModelBased Decomposition of Polarimetric SAR Covariance Matrices,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 49, No. 3, 2011, pp. 1104-1113. doi:10.1109/TGRS.2010.2076285
- S. R. Cloude, “Polarisation: Applications in Remote Sensing,” Oxford University, London, 2009, pp. 198-201. doi:10.1093/acprof:oso/9780199569731.001.0001
- J. J. Van Zyl, “Unsupervised Classification of Scattering Behaviors Using Radar Polarimetry Data,” IEEE Transaction on Geoscience and Remote Sensing, Vol. 27, No. 1, 1989, pp. 36-45. doi:10.1109/36.20273
- J. J. Van Zyl, M. Arii and Y. Kim, “Model-Based Decomposition of Polarimetric SAR Covariance Matrices Constrained for Nonnegative Eigenvalues,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 49, No. 9, 2011, pp. 3452-3459. doi:10.1109/TGRS.2011.2128325
NOTES
*Corresponding author.

