ABSTRACT

The prediction of coherent vortices with standard RANS solvers suffers especially from discretisation and modelling errors which both introduce numerical diffusion. The adaptive Vorticity Confinement (VC) method targets to counteract one part of the discretisation error: the one due to the discretisation of the convection term. This method is applied in conjunction with a hybrid RANS-LES turbulence model to overcome the overprediction of turbulence intensity inside vortex cores which is a typical deficiency of common RANS solvers. The third main source for numerical diffusion originates from the spatial discretisation of the solution domain in the vicinity of the vortex core. The corresponding error is analysed within a grid convergence study. A modification of the adaptive VC method used in conjunction with a high-order discretisation of the convection term is presented and proves to be superior. The simulations of a wing tip vortex flow are validated in terms of vortex velocity profiles using the results of a wind tunnel experiment performed by Devenport and colleagues (1996). Besides, the results are compared with another numerical study by Wells (2009) who uses a Reynolds Stress turbulence model. It turns out that the application of the modified adaptive VC method on the one hand reinforces the tip vortex, and on the other hand accelerates the axial flow which leads to a slight degradation compared to the experimental results. The result of Wells is more accurate close to the wing, but the result obtained here is superior further downstream as no excessive diffusion of the tip vortex occurs.

Keywords:

Tip Vortex, Adaptive Vorticity Confinement, Hybrid RANS-LES, Devenport, Numerical Diffusion

1. Introduction

Coherent tip vortices occur e.g. in the wake of lifting wings like aircraft foils, propeller blades or helicopter rotor blades and extend far downstream showing a slow decay. Considering the cases mentioned above, examples are wake encounters of aircrafts, cavitating propeller tip vortices that may damage the rudder and blade vortex in- teractions for helicopters.

Using Reynolds-Averaged Navier-Stokes (RANS) methods in conjunction with standard one- or two-equation turbulence models for the prediction of tip vortices leads to high errors, as the vortices smear out considerably faster in the simulation compared to the real flow. The increased dissipation results from artificial dissipation effects which are mainly dominated by two numerical errors. The first one is the discretisation error and the second one is the error due to insufficient turbulence modelling. Assuming an appropriate fine mesh in the vicinity of the vortex core, the discretisation error is dominated by the error introduced by the convection discre- tisation scheme. In conjunction with a second-order accurate flow solver, like Open- FOAM, most discretisation schemes, like e.g. linear upwind, introduce diffusive error contributions. These errors create numerical diffusion and lead to a strong dissipation of vortices. As mentioned above, the second numerical error that leads to artificial dissipation refers to turbulence modelling. Due to high velocity gradients inside the tip vortex core, linear isotropic Eddy Viscosity Models (EVMs) create a huge turbulent viscosity inside the core (compared with the physical viscosity). But the available experimental data show that tip vortex cores mostly contain almost laminar flow (see e.g. Devenport and colleagues [1] , pp. 68-69). Hence the turbulent viscosity contributes to a stronger (artificial) diffusion in the simulation compared to real flows. These numerical errors are analysed in greater detail in Section 2.

In this paper the potential of an advanced Vorticity Confinement (VC) method applied to a wing tip vortex flow is evaluated. The VC technique was proposed to improve the prediction of vortical flows where the accuracy suffers from numerical diffusion. The basic VC formulation and all modified ones require a user-defined proportionality factor that prescribes the strength of the reinforcement for the vortex. The main disadvantage of the these methods is the lack of a universal procedure to determine the appropriate factor. Even if the vortex was reinforced by VC, this would not necessarily provide a more accurate solution. The adaptive VC method, proposed by Hahn and Iaccarino (see [2] ), provides an exception. In this case, the strength of the vortex reinforcement is proportional to the estimated numerical diffusion due to the convection discretisation.

The overprediction of the turbulence intensity in the vicinity of the vortex core can be overcome using improved turbulence models. Some modified isotropic eddy viscosity models address the deficiency concerning coherent cortices introducing a curvature correction (see e.g. Spalart and Shur [3] for more information). Further improvement using the RANS approach has been shown using Second Moment Closures for instance in [4] and [5] , however, their performance remains limited. In this article, we concen- trate on a more basic approach and use a Large Eddy Simulation (LES) approach in the region of the vortex core. As the large vortices are resolved and not modelled, the local overprediction of turbulent viscosity is not forced by the vortex core flow. For the sake of simplicity we use a hybrid RANS-LES model (termed Detached Eddy Simulation- DES in the following) where the RANS models are applied in the vicinity of the wing. A hybrid RANS-LES approach is e.g. used also for the modelling of aircraft tip vortices (see e.g. Stephan et al. [6] ). We use the Spalart-Allmaras one-equation mixing-length model inside the RANS domain (for further information on the numerical setup see Section 5).

The adaptive VC method is employed in the present study in conjunction with a hybrid RANS-LES model. The first study analysing both methods in combination was published recently by the authors of this paper, see [7] . This former study compared the potential of the adaptive VC method in RANS simulations and hybrid RANS-LES using the same test case as in the present study. A minor modification of the adaptive VC method was presented there which will be focused in Section 3. Besides, a comparison between a RANS and a DES approach showed the superior potential of the adaptive VC method in conjunction with DES. Following, this study focuses with greater detail on the evaluation of the (modified) adaptive VC method in combination with DES turbulence modelling.

Presenting the adaptive VC method Hahn and Iaccarino used the upwind dis- cretisation scheme for the convection term successfully. Pierson and Povitsky [8] applied the adaptive VC method for the prediction of the flow of a convected Taylor vortex and a helicopter tip vortex. They used an Euler solver and realised the con- vection discretisation with an upwind, a linear upwind and a TVD scheme. It is not clear whether they adapt the calculation of the adaptive source term to the different schemes. In this study, the adaptive VC method is used with a linear upwind dis- cretisation of the convection term (termed LUDS) and the source term is adapted for consistency, see Section 3.2. Besides, Pierson and Povitsky restrict in most cases the zone where the VC source term is active by a minimal value of the local vorcitiy magnitude scaled to the maximum vorticity in the domain. Pierson and Povitsky observe an improved prediction of the tip vortex using the adaptive VC method. Nevertheless, as several assumptions are unknown or different to the present study, it is not possible to compare their conclusions to the ones gained in the following. In this study, the influence of a more general limiter will be analysed: restricting the VC source term to zones where vortex identification yields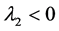. This is a common local vortex identification scheme: 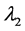is the second largest eigenvalue of the sum of the square of the symmetrical and anti-symmetrical parts of the velocity gradient tensor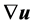, for more information see Jeong and Hussain [9] .

In this study, the adaptive VC method will be assessed in comparison with exper- imental data from Devenport et al. [1] . They carried out wind tunnel measurements of a tip vortex trailing from a NACA0012 wing at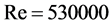. This data is well suited for the evaluation of adaptive VC, because the vortex is tracked until a long distance downstream, 30 times the chordlength. The setup and details concerning the measure- ment are described in section 4 and section 5 presents the simulation setup. Finally, Section 6 presents the simulation results, including an assessment of the adaptive VC method, the comparison to the experimental data and to the results obtained by Wells. Firstly, numerical errors with diffusive influence which can be termed to be the reason for using VC will be presented shortly in Section 2. Afterwards, Section 3 gives an overview of the VC technique and presents the modification of the adaptive method.

2. Artificial Dissipation

This section gives an overview over the numerical errors that dominate the artificial dissipation of coherent vortices. Referring to Lilek and Perić [10] (and Jasak [11] ), numerical solutions of fluid flows include three types of errors: modelling errors, discretisation errors and iteration convergence errors. Here, the focus is set on the first two types, as the iteration convergence errors can usually be reduced to a level with negligible influence.

Modelling errors are defined as the difference between the actual flow and the exact solution of the mathematical model, which is represented by the Navier-Stokes equations and the mass conservation (continuity) equation in this case. In case flows with coherent vortices are simulated, linear isotropic Eddy Viscosity Models (EVM) fail to predict the laminar vortex core and predict high values of turbulent kinetic energy instead. Common turbulence models based on linear, isotropic EVMs are e.g. the one- equation Spalart-Allmaras model [12] or two-equation models like the 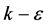or 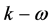model and their modifications. These models are based on the assumption that turbulence is created in regions of high mean velocity gradients. Although this is usually correct, this assumption fails in the vicinity of tip vortex cores where these models predict a huge production of turbulent kinetic energy. But, as Devenport and other authors observed, there is nearly laminar flow in the vicinity of the core. The overprediction of the turbulence production leads to an increased dissipation of the vortex and can therefore be termed as numerical diffusion.

In Large Eddy Simulations (LES) large (in relation to the discretisation in space and time) turbulent eddies are resolved and small ones are modelled. The advantage referring to coherent vortices is, that there is no overprediction of the turbulence intensity due to high velocity gradients around the vortex core. In conjunction with a hybrid RANS-LES approach, the near-field of the wing is modelled with a RANS approach saving computational effort.

The disretisation error introduces numerical diffusion in two different ways. The first one is insufficient grid resolution around the vortex core and can be overcome by mesh refinement. The second one is the discretisation of the governing equations. In the context of industrial flows with high Reynolds numbers, the convection term dominates the flow and hence its discretisation is important.

Usually, polynomial functions are used to describe the gradient of flow variables between grid points. In conjunction with the second-order accurate FVM the use of second-order accurate discretisation schemes would be reasonable as they preserve the overall (second-order) accuracy of the approach. A basic second-order accurate discre- tisation scheme is the central differencing scheme (termed CDS). But the use of second- order schemes for the convection discretisation may lead to numerical oscillations during the iterative solution process of the equation system. Following, schemes introducing diffusive truncation errors are usually used to assure stability. The stability is increased at the cost of accuracy. The total diffusion is then composed of the (anisotropic) numerical and the (isotropic) physical diffusion.

3. Vorticity Confinement

3.1. Overview

Vorticity Confinement describes a technique which reinforces vortices and therewith acts against the effects of artificial dissipation discussed in the previous section. As part of the VC approach an artificial source term is introduced into the momentum conservation equations, e.g. for incompressible flow

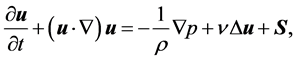(1)

with velocity, density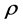, pressure 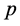and kinematic viscosity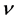. For different VC methods, 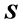can be generalized to

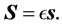(2)

The proportionality factor 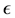(unit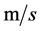) controls the strength of the source term, the vector 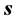(unit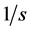) is defined by

(3)

where is the vorticity. Thus points along vorticity magnitude contour lines. (Different formulations of the vector are not considered in this study, because firstly the adaptive VC method-evaluated in this paper-uses the presented formulation and secondly the disadvantages listed subsequently refer to and cannot be com- pensated by another choice of.)

The influence of the VC source term was described smartly by Hahn and Iaccarino (see [2] ): Considering an axisymmetric vortex tube, where the vector points outward from the vortex centre, the source term convects vorticity back toward the vortex centre as it diffuses outward. They write the momentum conservation equation in rotational form to demonstrate the effect of VC: counteracting “the numerical diffusion by artificially generating stretching/tilting and convection flux”.

The original VC technique was proposed by Steinhoff and colleagues in 1992 ( [13] [14] [15] ). The factor was chosen to a user-defined value which is constant over the domain. Several authors improved this method including the local grid size and vortical fields (like the helicity) in the calculation of the source term. This improves the results of VC, but still there is no universal approach to determine the appropriate value of the user-defined factor. The trial and error approach to find the appropriate value is time-consuming and not reliable. A wrong choice leads to an unphysical vortex flow.

3.2. Adaptive Vorticity Confinement

The adaptive VC method introduces a momentum source term counteracting the error of the convection discretisation in an adaptive manner. The magnitude of the source term is proportional to the estimated numerical diffusion defined with the difference between the central scheme (introducing no diffusive error) and the utilised scheme.

Hahn and Iaccarino [2] proposed the adaptive VC method where is determined automatically based on an estimation of the numerical diffusion due to the convective discretisation. This leads to the advantage compared to all other VC methods that there is no need for a user-defined proportionality factor. Furthermore, the target of the adaptive method differs from all others. The adaptive method tries to compensate only for the numerical diffusion due to the convection discretisation whereas all other methods just reinforce vortices to compensate for any kind of dissipation. Following, it might be possible to generate stronger vortices with other methods compared to the adaptive method, but it would be questionable whether the stronger vortex is closer to the physically correct result.

The derivation of the adaptive VC method is based on the assumption that the numerical diffusion is known a priori, hence the total viscosity can be written as the sum of the (physical) viscosity and the numerical viscosity due to the con- vection discretisation

(4)

The target of the adaptive approach is to minimize the influence of on the vorticity field. This is the case if the confinement force cancels out the influence of the numerical viscosity. Based on Equation (1) in rotational form, Hahn and Iaccarino derived a definition of that is proportional to. The important point they stated refers to the estimation of the numerical viscosity. As explained in Section 2, the convection discretisation with CDS introduces no truncation error of diffusive type. Hence, the difference between the used discretisation scheme and CDS is related to the amount on numerical diffusion introduced using the scheme apart from CDS. As they used an upwind discretisation scheme for the convection term, the numerical diffusion is estimated by the difference between the central (CDS) and upwind discretisation (UDS) of the convection term

(5)

which has the unit. This is consistent to the overall numerical approximation as the confinement term approaches zero if the corresponding numerical diffusion vanishes. The adaptive definition for is the dot product of the difference with the vector divided by the squared magnitude of

(6)

for more information on the derivation see [2] .

In this study, the effect of restricting the adaptive VC source term to the vicinity of the vortex will be analysed. Therefor the local vortex identification criterion will be used: For, the adaptive source term will be set to zero.

In addition to the adaptive VC method presented above, there are further for- mulations of the VC method which lack the necessity for a user-defined forcing coefficient. These methods are termed “automatic” VC in the following and were presented by Costes and Kowani [16] [17] . The derivation of the automatic VC methods is based on the same approach as the adaptive one with a different final determination of. Besides, the automatic VC method is formulated also for another version of the directional part of the VC term presented in [15] . Automatic VC may offer an alternative to adaptive VC; a further study with a comparison of both methods is necessary to evaluate both its pros and cons. This research within this study is focussed on the evaluation and modification of the adaptive method.

3.3. Modification of the Adaptive Formulation

In this study, the adaptive method is used in conjunction with the high-order con- vection (HOC) scheme LUDS. Following, the difference in Equation (5) is calculated as the difference between CDS and LUDS, which is consistent to the target of cancelling out the effect of. Especially if the adaptive method is used in conjunction with HOC schemes, abrupt local unphysical changes of the sign of may occur in the vicinity of the vortex core (an example for LUDS is presented in Section 6.3). Basically, if the factor is positive, vortices are reinforced (see Equation (1)). If the sign of changes somewhere, the VC source term increases the effect of numerical diffusion in that place. Therefore, it is important to modify the adaptive method. An appropriate solution is using the absolute value of

(7)

This still scales with the magnitude of the numerical diffusion and always points along, hence convects the vorticity back to the vortex centre and acts against numerical diffusion. The effect of the original and the modified formulation on the evolution of a vortex will be shown in Section 6.3.

4. Test Case

In the present study, simulations are carried out for the experiments conducted by Devenport and colleagues [1] . In these wind tunnel experiments the evolution of the tip vortex generated with a NACA0012 wing was studied. Figure 1 shows a schematic view of the test section. The experiments were carried out in the Virginia Tech Stability Wind Tunnel located at the Virginia Polytechnic Institute and State University. The tunnel has a quadratic test section of 1.83 m width and 7.33 m length. The test case

consists of a rectangular NACA0012 profile with a span of m, a chord length of m and a blunt tip. The wing is attached at the centre of a wind tunnel wall. The velocity was measured using a four-sensor hot-wire probe. For further information on the apparatus and instrumentation see [1] .

There are two reasons why this experimental data is especially valuable for a comparison with numerical methods that target an improved resolution of tip vortices. The first one is the large distance downstream until where the vortex is tracked and the second one is the correction of the data for the wandering motion. Wandering describes the slow side-to-side movement of the vortex core which seems to occur usually in wind tunnels. The problem about wandering concerning measure- ments is that using time averaged results smooths gradients of the mean flow field in the vicinity of the vortex core. For example, the uncorrected velocity profiles through the core indicate a considerable decay of the vortex, whereas the corrected profiles show approximately no decay. The correction procedure is described in [1] . The authors state that most velocity fluctuations associated with wandering occur below the

frequency (free-stream velocity and chordlength) (see [1] , p. 99).

Devenport et al. suppose the reason of wandering to be a slight unsteady behaviour of the flow in the wind tunnel ( [1] , p. 100). This assumption is supported by several other studies they refer to.

Measurements are carried out for several Reynolds numbers and angles of attack. Besides, the flow in the boundary layer was tripped to introduce turbulence. The most extensive data set is available for, and tripping of the boundary layer flow between and of the chord; this setup is chosen for the comparison with the simulation. Within the measurements, further cases with different tripping are studied at: without tripping and with tripping between and of the chord. The vortex core parameter which is strongest influenced by the different tripping is the axial velocity at the vortex centre: it is reduced by about without tripping and increased by about with the longer tripping (compared to the result with tripping between and). Hence, the axial velocity is quite sensitive to the boundary layer flow.

For the setup chosen for comparison here, the tangential and axial velocity are measured in five times chord length distances until 30 times the chord length (behind the leading edge of the foil). Besides, the mean velocity {redcomponents and turbulence properties are measured at certain positions. A main outcome of the experiment is that the vortex core is laminar. The observed velocity fluctuations are attributed to the interaction of the vortex with the turbulent wake ( [1] , p. 101). The laminar flow could explain the slow decay of the vortex which manifests in nearly constant core parameters downstream of the foil.

5. Simulation Setup

The simulations are conducted with OpenFOAM 3.0.1 on a hexahedral mesh. Firstly, the computational domain and the mesh are presented, afterwards, the solver settings will be given. Figure 2(a) shows the computational domain and the (medium) mesh at certain boundaries.

The origin of the used coordinate system is located at the leading edge on the tip end of the foil. The x-axis points downstream and the y-axis points along the wing. This coordinate system is applied also in [1] , see Figure 1. The cross sections where the flow is analysed are located at. The inlet boundary is located at m and the outlet is located at m. The boundaries with y- and z-normals denote the walls of the wind tunnel’s test section. The size of the domain’s cross section is equal to the measuring section of the wind tunnel and also the placement of the wing in the cross section is identical.

The mesh is generated with Hexpress (version 5.1), Figure 2 shows the medium mesh. Besides, there are two meshes with a coarser and a finer mesh in the wake (see Figure 3). Until, all meshes are identical. At that point, the refinement of the wake region is coarsened for the medium and coarse mesh (for the medium mesh see Figure 2(d) or Figure 4). The coarse mesh is coarsened again at.

All meshes consist of eight base cells along the cross section length of the domain. For the medium mesh, the cells around the tip vortex are refined by seven steps in the y- and z-direction, hence the measured mean vortex core diameter m (mean value from to, see [1] , p. 81) would contain approximately eight cells (downstream of). For the coarse and the fine mesh, the measured vortex core would consist of about four and 16 cells respectively. The meshes contain approximately 3.9 M (coarse), 6.0 M (medium) and 20.0 M (fine) cells in total. As no wall functions are applied within the simulation, the first cell height is chosen to 2E−5 m which yields.

The bounding walls (normals y and z) are modelled by a slip boundary condition. Thus, the slight pressure gradient along the wind tunnel due to the boundary layer growth observed in the experiments cannot be modelled. It can be assumed that this effect is negligible for the evolution of the tip vortex. At the inlet the inflow velocity is

prescribed and a pressure boundary condition is applied at the outlet. The surface of the wing is represented by a no-slip condition and layer cells are used for the resolution of the boundary layer. At the inlet, the eddy viscosity is prescribed with

.

Devenport et al. do not indicate the free-stream velocity used in the wind tunnel tests. But they refer to preceding measurements conducted by Choi and Simpson [18] . They used the free-stream velocity m/s, this value is also used in the present study as is results in a reasonable kinematic viscosity value. To obtain the Reynolds number for the chord length we use the kinematic viscosity for air. The hybrid RANS-LES turbulence model (later

termed Detached-Eddy Simulation, DES) is based on the Spalart-Allmaras delayed DES model. The reference for the SpalartAllmarasDDES model can be found in [19] . A further remark concerns the laminar-turbulent transition (which is influenced in the experiments by the tripping) that is neglected here.

The simulations are conducted with the pimpleFoam solver, a large time-step transient solver using the PISO and the SIMPLE algorithms. Both algorithms are described e.g. by Ferziger and Perić [20] . The relaxation factor is set to 0.3 for all variables. The number of outer iterations (for the SIMPLE algorithm) during each time step is set to 20 with one pressure correction loop each. The time step is set to, which leads to a maximum Courant number of approximately 160 and a mean Courant number of about 0.1 in all simulations. Section 4 states an upper limit for the frequency below which most fluctuations associated with wandering occur. The corresponding period time is s, hence the wandering motion with the highest frequency is resolved in time by more than seven steps. Following, if wandering is self-induced by the trailing vortex, it will be possible to model this effect. The convection term of the momentum equation is discretised with a linear upwind discretisation scheme (LUDS). The time is discretised using the first order implicit Euler scheme.

A further remark concerns the source domain, where is introduced. It is not reasonable to apply a VC source term from any method in the whole computational domain. Inside the boundary layer zone each VC source term would introduce a huge amount of momentum as the vorticity magnitude is high there. This does not reinforce coherent vortices, but leads to a completely wrong prediction of the flow. In this study, the vicinity of the boundary layer is excluded from the region where the VC source is applied using a distance limiter. The VC source term is faded in as a function of the wall distance: starting from (about of the chord length) the source term is faded in linearly until the wall distance. Furthermore, the source term is active only between to avoid interactions with the inlet and outlet boundaries. Besides, the VC source term is faded in linearly in time after the con- vergence of the simulation without VC within 0.01 s.

6. Results

6.1. Overview

In the following section the simulation results will be analysed and compared to the experimental data. The simulation results are evaluated after s time each, by then the flow has passed the measurement region more than three times. The presented velocities are averaged values over a time period of s. Before showing results, the way how the velocity profiles are extracted from the simulation data is presented. These profiles will later be compared to tangential and axial velocity profiles through the core provided by Devenport et al. The procedure how the experimental data is processed to gain the velocity profiles is explained in Section 4. The corresponding procedure for the simulation data is described in the following. Therefore, it is important to state that the presented simulation results show the absence of vortex wandering. The temporal change of the vortex centre is at least several orders of magnitude smaller than the actual core radius. Even a reduction of the time step by a factor of eight showed no wandering effects on the medium mesh. This supports the conclusions given by Devenport et al., that wandering may originate from unsteady effects in the wind tunnel. Not all of these effects are captured by the model and setup, this refers e.g. to the inflow condition or the modelling of the wing with a completely fixed grid.

In this study the tangential and axial velocity profiles are gained from velocity evaluations on lines through the vortex core. Figure 5 shows four of these (dashed) lines as examples.

The coordinate system is shifted to the vortex centre represented here by the minimum value of in the plane. (The change of the vortex centre's location determined with different criteria is negligible.) The tangential and axial velocity is extracted on 32 lines with equal angular spacing around the vortex centre. Afterwards, the mean velocity profile is calculated as the average value for each radius from these lines. Based on these mean velocity profiles, the following vortex core parameters are determined: the peak tangential velocity, the core radius and the axial velocity at the vortex centre.

For the determination of the tangential and axial velocity components, the vortex axis is assumed to be parallel to the x-axis for the sake of simplicity. The angle between the vorticity vector at the vortex centre and the x-axis is less than 2˚ downstream of. The resulting error is considered negligible as it scales with the cosine of the angle. Thus the tangential velocity is defined as and the axial velocity

is simply.

The vortex core parameters (the radius, the peak tangential velocity and the axial velocity deficit) will be plotted at the x-coordinates of the measurement sections and at. Further upstream, there is no coherent tip vortex present in some cases, so that it would not be reasonable to calculate the core parameters.

The use of the VC method does not significantly increase the computational time. The time which a time step needs fluctuates by about. The difference between the mean value of simulations without VC compared to the same simulation with VC is less than.

In the following subsections, first the restriction of the VC source term to the zone in the vicinity of the vortex core will be analysed. Secondly the effect of the modified formulation according to Equation (7) will be discussed. Afterwards, the simulation results will be compared to the experimental data.

6.2. Restriction of the VC Source Term to Zones with

The influence of the restriction of the VC source term to the vicinity of the vortex core will be analysed in the following. As will be shown in the next section, the modified formulation presented in Section 3.3 is superior compared to the original one, so the modified VC source term according to Equation (7) will be used here. The reason for the restriction is the acceleration of the axial flow due to the source term outside of the vortex core in some places. In these places, the magnitude of the source term is comparable to the maximum value in the plane perpendicular to the current vortex axis and the source vector is quasi parallel to the vortex axis (with a deviation of a few degrees). Although drops to a negligible value outside the vortex core, the value of becomes so high that it outbalances the small. To suppress this effect, the VC source term can be restricted to exclude the zones that introduce high axial momentum. In this study, the source term is restricted to cells with. Hence, the VC source term is activated only inside the vortex core and in the vicinity of the free shear layer.

Figure 6 shows the influence of the restriction of the source term on the evolution of

the vortex core parameters. The comparison to the experimental results is evaluated in subsection 6.4. In both cases, the application of VC reduces the vortex core size and increases the peak tangential velocity which corresponds to a stronger vortex. The disadvantage of the unrestricted source term reveals in the large overprediction of the axial velocity at the vortex centre: Further downstream, the axial velocity deficit nearly vanishes. Furthermore, the unrestricted source term induces velocity fluctuations close to the trailing edge. This effect manifests in the sudden drop of just downstream of and was observed also on the coarse and fine mesh. In the following only the restricted VC source term will be used. This reduces a little the improved prediction of the core size and peak tangential velocity but assures a comparable good prediction of the axial velocity.

The magnitude of the adaptive VC source term is large in the vicinity of the vortex core radius (where changes its sign). Hence, it would be interesting to further study less restrictive vortex identification schemes like the or the criterion (both for values larger than zero) in conjunction with the restriction of the VC source zone. This may lead on the one hand to an increase of the vortex strength on the other hand to an acceleration of the axial flow.

6.3. Modification of the Adaptive Formulation

First, the necessity of the modification for the adaptive VC formulation, presented in Section 3.3, will be discussed. Afterwards, the effect of the modification on the vortex flow will be shown. Figure 7 shows cross sections through the vortex core at. The grid is represented by the grey square pattern, the thin black circular lines indicate the border of the vortex core and are determined with. The vector that prescribes the direction of the VC source (see Equations (2) and (3)) is represented by

arrows (which are not projected to the plane). The grey cells indicate cells where, hence, there the direction of the source term changes and points against the tangential velocity of the vortex. The simulation results in Figure 7 are obtained without the VC source term being active, applying the upwind differencing scheme (UDS) or LUDS for the convection term.

The vortex core has an approximately cicular shape in both cases. For LUDS, the vortex core is smaller and the vector larger which corresponds to the improved approximation using the HOC scheme. The vector field shows a smooth behaviour and indicates the rotation of the vortex flow. The magnitude of increases towards the vortex centre. If the discretisation scheme UDS is used, only some cells show a negative value. In case of LUDS, a lot more cells with exist. The con- sequentail abrupt change of the direction of the VC source can be omitted by means of the modified formulation presented in Equation (7).

Figure 8 shows the effect of different formulations of the adaptive VC source term on the evolution of the vortex core size and the peak tangential velocity. The simulation results were obtained on the medium mesh using LUDS for the convection discre- tisation. The simulations are conducted without VC (w/o VC), with the original adaptive VC method and with the modified adaptive VC method. Besides, as is negative in many cells for LUDS (see Figure 7), the simulation is

conducted also with a negative source term.

The original VC method leads to a slightly increased core radius and slightly reduced tangential velocity compared to the result without VC. This corresponds to the source term acting in the wrong direction in many cells. If the original source term is multiplied with, a reduced core size and an increased velocity are predicted. This variant should not be applied generally. The purpose is to show that is mostly negative in the vicinity of the vortex core and hence this negative source term reinforces the vortex strength. The modified formulation with leads to the smallest core size and highest peak tangential velocity. The overprediction of the peak velocity at upstream locations will be discussed below. All in all, this shows the advantage of the modification.

6.4. Comparison of the Experimental and the Simulation Results

In the following subsection, the velocity profiles through the vortex core and the core parameters from the experimental results and the simulation results will be compared. Therefor, the modified formulation of the adaptive VC source term will be used and restricted to zones with (for more information see the remarks above). Figure 9 shows the averaged tangential and axial velocity profiles for the first and last measurement section. Subfigure 9a shows that both the peak tangential velocity and the core radius increase with increased mesh resolution and with active VC. Besides, the gradient inside the vortex core that represents a part of the vorticity magnitude increases in the same manner. This is consistent as a finer mesh and the VC method reduce the amount of numerical diffusion and hence lead to a stronger vortex. The profile of the experimental data indicates a two-layered structure with an inner and outer core (see [1] , p. 94). This effect does not occur in the simulation; one reason for this may be insufficient resolution. Besides, the simulation overpredicts the peak tangential velocity in some cases, but the gradient is still larger in the experimental result.

Further downstream at the effect of mesh refinement and applying VC is similar to, as the vortex strength is increased on the finer mesh and with VC. For the shown cases, the influence of the refined mesh prevails the influence of VC. The inner core that occurred in the experiment further upstream vanished, so the gradient of the result with VC on the fine mesh is closer to the experimental result here than at. The results do not show grid convergence. Hence, it would be necessary to further refine the fine mesh to estimate the numerical error due to the spatial discretisation. If the wake is refined by a factor of two like for the given meshes, the total cell count will be about 150 million. As this would lead to excessive computational costs, another approach like Adaptive Mesh Refinement (AMR) would be reasonable to study grid convergence.

Figure 9(c) and Figure 9(d) show the axial velocity deficit through the vortex core. At, the simulation result does not approach the experimental one as the mesh is refined, but there is no clear tendency also. And the deviation of the simulation

results to the experimental one (at) is between and. This indicates that another effect apart from the local mesh resolution is responsible for the axial velocity evolution. For a further discussion see below. Applying VC leads to an increase of the axial velocity which impairs the result in comparison with the experimental data. The fluctuations in the profile of the fine mesh with VC may indicate a deformation of the vortex that dies away further downstream or in all other cases. Downstream at, the result obtained on the fine mesh approximates best the experimental data, nevertheless, the deviation is still large. Again, the use of VC accelerates the axial flow.

The vortex core parameters are shown in Figure 10. The comparison to the results which are presented by Wells [21] will be analysed in the next subsection. The experimental result shows an almost constant core radius with little oscillations behind, see Figure 10(a). This is different in case of the simulation: The vortex core

size monotonically increases with distance downstream. Upstream of, the absolute deviation between the simulation results vanishes, because the mesh is equal there. For the coarse mesh with VC, the core radius increases from to by about, for the fine mesh with VC, the increase is significantly less: approximately. Downstream of, the refinement from coarse to medium reduces the core radius by about (with and without VC) and the refinement from medium to fine leads to a reduction of about (with and without VC). There, the effect of VC is a reduction of the core radius by about for the coarse and medium mesh and by about for the fine mesh. Hence, the potential of VC to reduce the core size depends very little on the mesh size in these cases. Compared to the experimental data, the best result (with VC using the fine mesh) leads to an over- prediction of the core radius of about at.

The peak tangential velocity is shown in Figure 10(b). Without applying VC the following effect can be observed: The finer the mesh is, the closer the simulation result is to the experimental result. Applying VC on the fine mesh leads to an average over- prediction of the peak velocity by about (downstream of). Referring to Figure 5, this does not necessarily lead to an overprediction of the velocity gradient inside the vortex core. Between and, the peak velocity decays between (coarse mesh with VC) and (fine mesh with VC). This change is considerably less than the relative change of the core radius (between and). This would mean, that it is easier to predict the correct (compared to the experiment) peak velocity as the core size with this setup. Downstream of, the simulation results increase with each refinement step in average by approximately. There, the use of VC increases the predicted velocity in average between (coarse and medium mesh) and (fine mesh). Hence, the potential of the adaptive VC method to increase the peak tangential velocity is largest for the fine mesh. Considering the vortex core size and the peak tangential velocity, the VC method increases in all cases the vortex strength.

Figure 10(c) shows the axial velocity deficit at the vortex centre. The best result (compared to the experimental one) is obtained without VC on the fine mesh, the average deviation is approximately (downstream of). At upstream positions, there is a minimum of the velocity deficit predicted on the coarse and medium mesh near. On the fine mesh, only a small drop of the axial velocity deficit occurs. But the point is that although the result on the fine mesh should be more accurate than the ones on the coarser meshes, the result around is worse compared to the experimental data. This indicates that another effect apart from the spatial resolution of the vortex core is responsible for the overprediction of the axial velocity. As indicated in Section 4 (based on the experimental data), the boundary layer development and therewith the free shear layer has a large influence on the axial velocity at the vortex centre. Following, it would be necessary to study further the boundary layer flow and the evolution of the free shear layer and also its influence on the tip vortex to gain explanations for the deviations in Figure 10(c).

Applying VC reduces the axial velocity deficit in each case. The relative reduction of the axial velocity deficit downstream of is approximately for the fine mesh and about for the medium and the coarse mesh. The relative acceleration of the axial flow due to VC in terms of is much less: about on the fine mesh and about on the medium and coarse mesh (average value downstream of). Although the target of the adaptive VC method is to reinforce vortices, it accelerates the axial flow which deteriorates the simulation results compared to the experimental result. Before the influence of the adaptive VC method on the prediction of the axial velocity can be assessed finally, it is necessary to obtain better results of the axial velocity without VC. A possible solution is the use of Reynolds Stress Models as will be presented in the next subsection.

6.5. Comparison to Another Numerical Study

In the following, the results presented above will be compared to the results obtained in the study by Wells [21] , who used the same test case as in this study. Wells analysed the influence of different RANS turbulence models on the prediction of tip vortices: the Reynolds Stress Model (RSM) based on [22] and the Spalart-Allmaras one-equation mixing-length model with and without curvature correction. The main conclusion was that the result obtained with the RSM is superior and gives good agreement with the experimental velocity profiles and turbulence patterns. Like in this study, Wells neglected the laminar-turbulent transition.

In this subsection, the best result obtained by Wells will be compared to the results obtained in this study. The best result in [21] was obtained on a structured grid with 11.9 M cells using wall functions and the RSM. Unfortunately, there is no information given on the grid resolution in the vicinity of the vortex core.

The velocity profiles Wells evaluated were extracted on a line parallel to the z-axis through the vortex centre. The vortex core parameters were determined from the resulting profiles. The influence of the different procedures to extract core parameters that were used by Wells [21] and in this study are assumed to be small in relation to the change of the values which Wells observed between and.

Wells evaluated the simulation results only until, as he remarked excessive dissipation of the tip vortex further downstream. Figure 10 shows that the relative change Wells obtained between and is higher than the change predicted in any case of this study. The important difference between the results in [21] and in this study is, that Wells achieved a very good prediction of all three core parameters at. But downstream, the deviation to the experimental result is very high compared to the other presented results. As the use of the RSM approach leads to the good result at, it is questionable why the result becomes this bad at. A possible reason may be a change of the mesh quality. Nevertheless, it would be reasonable to try different turbulence models like the RSM approach in conjunction with adaptive VC and with the setup in the present study.

7. Conclusions

The original adaptive VC method presented by Hahn and Iaccarino mitigated the vortex, because the source term reversed in conjunction with the linear upwind dis- cretisation of the convection term. The modified formulation is based on an evaluation of the magnitude of the estimated numerical diffusion and neglects its fluctuating direction. This modification turned out to be superior compared to the original for- mulation.

The modified, adaptive VC method improved the prediction of vortices in some aspects. It led to a reduction of about of the vortex core size which is an improvement compared to the experiment. Besides, the use of VC increases the peak tangential velocity (in average by about) and leads to an overprediction in some cases. The axial flow at the vortex centre is accelerated in average by about due to the application of VC which increases the deviation to the experimental results (the relative change of the velocity deficit is obviously larger). Compared to the original method’s formulation by Hahn and Iaccarino, this deficiency could be significantly reduced restricting the VC source term to zones with, hence to the vicinity of the vortex core.

Compared to results obtained with a Reynolds Stress turbulence Model (RSM) (by Wells), the results obtained with VC and the underlying hybrid RANS-LES approach lead to less accurate results at the most upstream measurement section but to superior results further downstream. In this study, the diffusion of the vortex core could be limited to an acceptable level unlike in the other numerical study using the RSM. A possible reason for the difference of further downstream is a coarsening of the mesh resolution in the RSM case. It would be interesting to further study the potential of the (modified) adaptive VC method in conjunction with other turbulence models (e.g. RSM), especially with respect to the relation of the boundary layer flow and the axial velocity near the vortex. Subsequently, the acceleration of the axial flow due to VC should be analysed further.

The used mesh resolutions with a total cell count of up to 20 M don’t show grid convergence. To assess the influence of numerical diffusion due to domain discre- tisation, Adaptive Mesh Refinement would be necessary to keep the total cell count to an acceptable level.

Acknowledgements

The investigations presented in this paper have been obtained within the research project “Entwicklung von numerischen Methoden zur Auflösung konzentrierter Wirbelstrukturen” (Development of Numerical Methods for the Resolution of Coherent Vortices) funded by the Deutsche Forschungsgemeinschaft (DFG). This support is greatly appreciated.

Cite this paper

Feder, D.-F. and Abdel-Maksoud, M. (2016) Tracking a Tip Vortex with Adaptive Vorticity Confinement and Hybrid RANS-LES. Open Journal of Fluid Dynamics, 6, 406-429. http://dx.doi.org/10.4236/ojfd.2016.64030

References