Open Journal of Fluid Dynamics
Vol.05 No.01(2015), Article ID:54915,6 pages
10.4236/ojfd.2015.51011
Experimental and Numerical Investigations on Plate-Type Heat Exchanger Performance
Yasuyuki Ikegami, Sami Mutair, Yusuke Kawabata
Institute of Ocean Energy, Saga University, Saga, Japan
Email: ikegami@ioes.saga-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 December 2014; accepted 17 March 2015; published 23 March 2015
ABSTRACT
Low-grade Thermal Energy Conversion (LTEC) is a potential source of renewable energy. One of its forms is the Ocean Thermal Energy Conversion (OTEC) in which the temperature difference between the warm surface water and the cold deep water of the ocean is utilized in driving a heat engine cycle. Unlike the conventional thermal power generation systems, the temperature difference between the heat source and heat sink in OTEC system is relatively small. Therefore, efficient heat exchangers should be used since heat exchangers play a major role in the overall system performance and economics. Due to their efficiency even in operating at small temperature difference, plate heat exchangers are strong candidates in OTEC systems. In this study, performance of a herringbone plate-type heat exchanger is experimentally investigated. Moreover, numerical simulation results obtained by using Fluent CFD software are compared with the experimental re- sults and found in good agreement.
Keywords:
CFD Simulation, Nusselt Correlation, Plate Heat Exchanger

1. Introduction
Plate Heat Exchangers (PHE) have been increasingly used in the past decades, not only in chemical and food processing industries for which it was originated in the 1930s, but also in wide range of industrial and energy application. This is due to their compactness, effectiveness in transferring heat, bio-fouling resistance and the ease of dismantling, cleaning, and also the ease to adapt to changes in thermal demand. For the optimal design of PHE, their thermal and hydraulic characteristics should be predictable in the intended duty. Muley and Manglik [1] investigated the effect of chevron angle and the enlargement factor for three different plates in single pass counter flow arrangement. They investigated the effect of chevron angle and enlargement factor on the pressure drop in the range of 600 < Re < 1000 and compared the results with those obtained from experiment conducted using flat. Comparison shows that the heat transfer rate increases 2 - 5 times larger than that of flat plate upon an increases of the chevron angle; however, the pressure drop have increased from 13 to 44 times compared with the flat plate.
Owing to the flexibility and modular design of plate heat exchangers, a wide range of PHEs that suits specific needs is offered; however, evaluation of the PHE thermal and hydraulic characteristics experimentally can be costly especially when testing sophisticated plate patterns and when using expensive corrosive resistant materials. Therefore, evaluation of the PHE performance in specific duties using numerical methods can be very helpful and time and budget saving. Computational fluid dynamics (CFD) software provides a powerful tool for this purpose and has shown reliability for closely predicting the performance of various types of heat exchange devices. In this work, the thermal characteristics of a given plate heat exchanger is experimentally evaluated, and compared against the date obtained from Ansys Fluent CFD software. Performed analysis indicates good agreement between the experimental and the numerical results at the investigated range of variables.
2. Experimental Setup
Experimental setup is shown in Figure 1 and consists of two loops through which the warm water and the cold water exchange heat in counter flow at the plate heat exchanger, temperature sensors and differential pressure sensors are installed at the inlets and the exits of the plate heat exchanger to monitor the temperatures and pressure difference at these locations. The flow velocity in the heat exchanger is controlled by using electromagnetic flow meters installed at the inlet ports of the heat exchanger. Two pumps circulate the warm and cold water obtained from the respective tank at the desired temperature and flow velocity. The tested brazed plate heat exchanger is constructed from 8 plates made of stainless steel SUS316L with 65 degrees chevron corrugation, and arranged to form single pass looped flow. Photo of the tested plate is shown in Figure 2 while Table 1 shows the specifications of the PHE. Data is collected under steady state condition which is ensured through constant temperatures and mass flow rates.
3. Heat Transfer Correlation
In general, the heat transfer correlation for a fluid flow past a solid surface is expressed in a dimensionless form
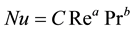 (1)
(1)
where Nu is the Nusselt number evaluated as:
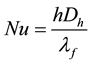 (2)
(2)
where h is the convection heat transfer coefficient, Dh is the hydraulic diameter of the channel, and λf is the
Figure 1. Schematic diagram of the experimental setup.
Figure 2. Photo of the tested plate.
Table 1. Heat exchanger specifications.
thermal conductivity of the fluid. The coefficient b in the above equation is widely taken as 1/3 [2] and this value is used in the current correlation.
 (3)
(3)
and
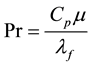 (4)
(4)
where De ≈ 2b.
Thermo-physical properties of the fluid are calculated at average inlet and outlet temperature.
The overall heat transfer coefficient U is calculated as:
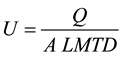 (5)
(5)
where A is the heat transfer area and LMTD is the logarithmic mean temperature difference evaluated as:
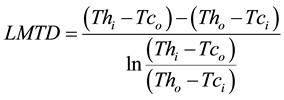 (6)
(6)
The heat transfer rate Q in Equation (5) is calculated from the temperature difference between inlet and outlet flow as:
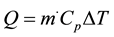 (7)
(7)
where  is the mass flow rate of water and Cp is the specific heat at constant pressure and
is the mass flow rate of water and Cp is the specific heat at constant pressure and 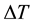 is the difference between the inlet and outlet water temperatures.
is the difference between the inlet and outlet water temperatures.
Also, the overall heat transfer coefficient U is calculated from the heat transfer rate from the hot water side to the cold water side across the plate wall as:
 (8)
(8)
Assuming hc = hh due to the equality of flow velocities in the cold and hot water channels, the convective heat transfer coefficient at the plate wall is then evaluated as:
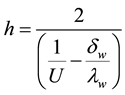 (9)
(9)
where 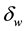 and
and 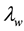 are the plate’s thickness and thermal conductivity, respectively.
are the plate’s thickness and thermal conductivity, respectively.
4. Experimental Results
In each experimental run, mass flow rates of warm and cold water were adjusted to yield equal velocities in the cold water channel and the hot water channels that ranged from 0.3 - 0.9 m/s. All experiments were conducted using tap water at fixed temperatures of 15˚C and 30˚C for the cold water side and the hot water side, respectively.
Figure 3 shows variation of the overall heat transfer coefficient and the convection heat transfer coefficient with flow velocity at the hot water side and the cold water side of the PHE. Both coefficients are seen to increase linearly with an increase of the flow velocity due to the increase of turbulence level. Figure 4 shows a dimensionless correlation between Reynolds number and Nusselt number divided by Pr1/3. All points are seen to lie on a single straight line that shows proportional relation between Re and NuPr−1/3 for the investigated range of Reynolds number.
5. CFD Simulation
Large number of studies has been conducted for the simulation of thermal-hydraulic characteristics for various
Figure 3. Variation of overall and convection heat transfer coefficients with flow velocity.
types of heat exchanger at wide operation ranges. Galezzo et al. [3] have shown good agreement between the simulation and experimental works preformed on an FT-43 PHE for different flow configurations at Reynolds number that ranged from 93 to 894. Also, this work has presented information about temperature and velocity distribution inside the flow channel.
In the present work, a tetrahedral mesh of about 7.5 million cells was generated for five zones (three plates enclosing two fluid channels) as shown in Figure 5. Inlet and outlet ports of the PHE were extended in order to avoid reverse flow at the outlets. Mesh was created using Gambit software and then exported to the CFD solver for simulation.
The realizable k-ε model is used for turbulence modeling and the solution is considered converged if the continuity, turbulence and energy residuals fall below 0.001. The inlet temperatures for the cold water side and the hot water side were fixed throughout the simulation at 5˚C and 30˚C, respectively. Heat transfer was simulated for flow velocity that ranged from 0.1 - 0.9 m/s. In each simulation run, the flow velocity was fixed in the cold water and hot water channels.
Figure 4. Characteristics of plate heat exchanger expressed as correlation of Nusselt number with Reynolds number.
Figure 5. Drawings of the investigated PHE geometry and the calculation grid.
Figure 6 shows a dimensionless correlation between Reynolds number and simulated Nusselt number for hot and cold water sides divided by Pr1/3. The experimental results are also presented in this graph for comparison. It is clear that the simulation results are so far comparable to the actual pleat heat exchanger performance. If a single fitting curve is made to represent the experimental and simulation data together as shown in Figure 7, the best fitting curve is described by the following equation:

6. Conclusion
Heat transfer performance of a chevron plate heat exchanger is with 65˚ chevron angle. Comparison between the two methods has shown good agreement for the investigated variable range.
Figure 6. Variation of simulated Nusselt number with Reynolds number.
Figure 7. Curve fitting of the experimental and simulation Nusselt number.
Heat transfer performance of the tested plate is expressed by Nusselt number correlation shown in Equation (10); however, this correlation doesn’t entail the wall to bulk dynamic viscosity ratio since the temperature readings at the plate wall are not collected in the conducted experiments.
References
- Muley, A. and Manglik, R.M. (1999) Experimental Study of Turbulent Flow Heat Transfer and Pressure Drop in a Plate Heat Exchanger with Chevron Plates. Journal of Heat Transfer, 121, 110-117. http://dx.doi.org/10.1115/1.2825923
- Muley, A. (1997) Heat Transfer and Pressure Drop in Plate Heat Exchangers. Ph.D. Dissertation, Mechanical Engineering, University of Cincinnati, Cincinnati.
- Galeazzo, F.C.C., Miura, R.Y., Gut, J.A.W. and Tadini, C.C. (2006) Experimental and Numerical Heat Transfer in Plate Heat Exchanger. Chemical Engineering Science, 61, 7133-7138. http://dx.doi.org/10.1016/j.ces.2006.07.029









