Received 17 February 2015; accepted 25 March 2015; published 27 March 2015

ABSTRACT

An idea on interfacial equilibrium-potential differences (Df_eq) which are generated for the extraction of univalent metal picrate (MPic) and divalent ones (MPic₂) by crown ethers (L) into high-po- lar diluents was improved. These potentials were clarified with some experimental extraction- data reported before on the M = Ag(I), Ca(II), Sr(II) and Ba(II) extraction with 18-crown-6 ether (18C6) and benzo-18C6 into 1,2-dichloroethane (DCE) and nitrobenzene (NB). Consequently, it was demonstrated that the Df_eq values from the extraction-experimentally obtained logK_D,Pic ones are in agreement with or close to those calculated from charge balance equations in many cases, where the symbol, K_D,Pic, denotes an individual distribution constant of Pic⁻ into the DCE or NB phase. Also, it was experimentally shown that extraction constants based on the overall extraction equilibria do not virtually contain the Df_eq terms in their functional expressions.

Keywords:

Extraction Constants, Distribution Constant of a Single Ion, Interfacial Equilibrium-Potential Differences, 1,2-Dichloroethane, Nitrobenzene, Metal Picrates, Crown Ethers

1. Introduction

Univalent and divalent metal picrates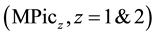, such as alkali and alkaline-earth metal ones, have

been extracted by crown compounds (L) into the high-polar diluents, such as 1,2-dichloethane (DCE), dichloromethane and nitrobenzene (NB) [1] -[5] . In such high-polar diluents, an extracted ion-pair complex, MLPic_z, dissociates ML^z+ and zPic⁻ [1] -[3] [6] . In introducing these component equilibria in an extraction model, an individual distribution constant (K_D,A) of Pic⁻ (=A⁻) into the diluents has been determined extraction-experimen- tally [1] -[3] [7] . However, in spite of the limitation of the same K_D,A definition and the same diluents, the thus-determined K_D,Pic values have differed from each other. For example, the logK_D,Pic values were −0.94 [2] for the PbPic₂ extraction with 18-crown-6 ether (18C6), −1.34 [7] for the SrPic₂ one with benzo-18C6 (B18C6) into NB, −2.4₆ [3] for the AgPic one with benzo-15-crown-5 ether, −1.89 [2] for the PbPic₂ one with 18C6 and −4.3₅ [6] for the CdPic₂ one with 18C6 into DCE. Thus, their values have changed over experimental errors with combinations of MPic_z and L.

To clarify a reason for such differences, the authors have applied the idea [8] of an interfacial potential dif-

ference (Df_eq) at extraction equilibrium to an expression of log K_D,A, namely 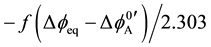[3] [6]

[7] , where the negative sign being in the front of f, which denotes F/RT, comes from the electrical charge of A⁻. In addition to this, extraction constants, K_ex± and K_ex2±, have been electrochemically expressed as

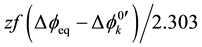at and 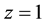and at ex±, ex2± and 2 [3] [7] . Here, 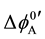and 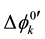refer

to standard formal potentials for the single distribution of A⁻ into the diluent or organic (o or org) phase and the formal potentials for the overall equilibrium, respectively. Also, K_ex± and K_ex2± have been defined experimentally

by extraction as [2] [7] or 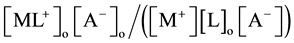[1] -[3] and [7] , respectively.

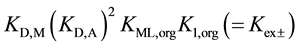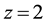On the other hand, from the thermodynamic points of view, these extraction constants are resolved into for [7] , 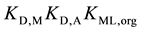for 1 [3] and

for 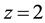[7] . Here, the component equilibrium constants, K_ML,org (complex

formation in the o phase) and K_1,org (1st-step ion-pair formation in the o one), do not contain the Df_eq terms in their expressions, because the constants are of homogeneous systems that all species relevant to the reaction are present in the single o phase [3] [7] ; namely no interface is involved in these processes. Similarly, the distribution constant of M^z+ has been expressed with K_D,M (see Equation (3) at 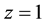in the Section 2.1) [3] . Therefore,

since K_D,M and K_D,A are present in the or term, the both terms must cancel out mu-

tually the Df_eq ones. Thereby, the extraction constants virtually lose the Df_eq terms on their functional expres-

sions. Thus, the above expression, such as, has caused contradictions on the thermodynamic cycles [3] [7] . Furthermore, such contradictions can cause discrepancies in between

experimentally-evaluated values and theoretically-reproduced ones [7] .

In the present paper, in order to solve the above two contradictions, namely the differences of K_D,A caused by experimental conditions of extraction and the contradiction based on the thermodynamic cycles [3] [7] , we proposed another expression without Df_eq of the extraction constants, K_ex± and K_ex2±. In course of clarifying this expression, some experimentally-determined constants [3] [7] , such as K_ex±, an individual distribution constant (K_D,ML) of the complex ion ML²⁺ into the NB phase and that of AgL⁺ into DCE, were also reproduced by calculation. Here, the AgPic and MPic₂ (M = Ca, Sr & Ba) extraction with L = 18C6 and/or B18C6 [3] [7] were employed as model systems. Also, a meaning of the Df_eq values [3] [7] & [8] which were calculated from the logK_D,A ones determined by the extraction experiments was discussed based on an electroneutrality-point of view [8] for the o phases. Moreover, the thus-obtained expressions for the extraction constants were applied to other types of extraction systems with o = DCE and NB.

2. Theory

2.1. Df_eq Values Derived from Charge Balance Equations for the o Phase

(i) Case of the M(I) extraction with L. For the extraction equilibrium, , we can obtain from the extraction model (see Appendix I for more details) reported before the following charge-balance equation

(1)

for the o phase. The concentrations of M⁺ and A⁻ in the o phase were modified as

(2)

by using electrochemical equations [6] [8] such as

(3)

and

(4)

see Appendix B in ref [6] for a detailed derivation from electrochemical potentials to this equation. Here, and [j]_o/[j] denote a standard formal potential of species j {=M(I), A(−I) & ML(I); see the introduction and section 3.3} and the individual distribution constant (K_D,j) of j between the two phases, respectively. At least, the values are available from references for M = Ag(I) [9] , Ca(II) [10] , Sr(II) [10] and Ba(II) [10] and A = Pic(−I) [11] into the DCE and NB phases. Additionally, the

values have been determined extraction-experi- mentally [1] -[3] [6] [7] ; see Appendix II for the K_D,A determination. Defining as and then rearranging Equation (2), we can easily obtain

(5)

with

(5a)

(5b)

and

(5c)

Accordingly, the following equation is derived.

(6)

Hence, if the [M⁺], [ML⁺]_o and [A⁻] values are determined experimentally, then we can obtain the Df_eq values from Equation (6) immediately; the [ML⁺]_o values were calculated here from the relation

with (see Appendix II for more detail) and. The data of [ML⁺]_o £ 0 were neglected in a further computation.

(ii) Case of the M(II) extraction with L. Similarly, we can consider the following stepwise extraction-equili- bria [6] [12] at the same time: (see Appendix I for a basic extraction model and Appendix II for the K_D,A determination). Therefore, the charge balance equation for the o phase becomes

(7)

As described above, this equation was modified to [8]

(8)

Defining as and then rearranging Equation (8), we easily obtain the cubic equation

(9)

with

(9a)

(9b)

and

(9c)

We can exactly solve this equation for x based on the mathematical formula [13] . Its real solution is

(10)

where and. Therefore, we can similarly obtain the Df_eq value from the combination of Equations (6) and (10).

The b¢ values were evaluated from the relation, with and 2, where (under the condition of [7] ). The values were directly determined by AAS measurements in the

extraction experiments [2] [7] and also we were able to calculate the other values in r₊ from the experimental data [7] .

2.2. On Expressions of the Extraction Constants without Df_eq

According to previous papers, the two of the three extraction constants have been defined as for the M^IA-L extraction system [3] and and for the M^IIA₂-L extraction one [7] . Here, logK_ex± (or logK_ex2±) equals (or) at.

These two kinds of extraction constants contain the Df_eq terms as parameters in their functional expressions[3]

[7] . On the other hand, logK_ex has been expressed as or without Df_eq and spontaneously became an expression electrochemically-standardized at [3] [7] .

In the above functions, some contradictions have been observed in the former cases: see Appendix in ref. [7] . As an example similar to that described in the introduction, the relation,

, must give a function without Df_eq, because

the resulting component equilibrium-constant K_2,org does not relate with Df_eq [7] ; namely K_2,org and K_ex are the constants at. However, using the above definition [3] [7] , the same term, , be-

comes and then the Df_eq term does not disappear, where and. The same is also true of the result of which is defined as. These two facts obviously have the contradiction with respect to Df_eq.

In order to cancel such contradictions, we assume here that the two extraction constants are functions without Df_eq, as well as that of K_ex [3] [7] . Accordingly, the constants are defined as

(11)

and

(12)

That is, by our traditional sense, it is proposed here that complicated equilibrium constants, such as K_ex, K_ex± and K_ex2±, do not contain the Df_eq terms in their functions. This means that these constants are ordinarily defined without Df_eqor under the condition of and thereby are electrochemically-standardized as and [3] [7] . Table 1 lists new (or traditional) expressions of such extraction constants composed of some component equilibrium constants based on thermodynamic cycles.

The relations in Table 1 shows that the individual distribution process of A⁻ [12] cancels out that of a cation [14] , such as M⁺, R₄N⁺, M²⁺ and ML²⁺, in Df_eq. As an example, the thermodynamic relation for M(II)

(13)

can be rearranged into

(14)

^ak = ex±, ex2±, ML,org, ML,w, & 1,org, where the symbol “w” shows a water phase; ^bThermodynamic cycle; ^cRef. [3] ; ^dRef. [7] .

Therefore, the relation (c) in Table 1 is immediately obtained. From Equations (2) and (8), one should obviously see that Df_eq of K_D,M equals that of K_D,A in the extraction system of Equation (13). Also, we can rewrite Equation (13) to

(13a)

Consequently, Equation (14) or (13) does not contain the Df_eq term and is virtually expressed with only the standard formal potentials (at) as Equation (13a). The thermodynamic relations are also satisfied with the expressions such as Equations (11) and (12). The same is true of the other relations in Table 1.

3. Results and Discussion

3.1. On a Meaning of Df_eq Estimated from log K_D,A

Table 2(a) lists fundamental data [3] for the extraction of AgPic by B18C6 into DCE. The Df_eq values were calculated from Equation (4) and the experimental log K_D,Pic values in Table 2(a).

Here, [11] at 298 K was employed in the calculation.

^aValues calculated from at 298 K; ^bValues calculated from; ^cUnit: mol dm⁻³; ^dRef. [3] ; ^eValues re-calculated from the same data as that reported before. See ref. [3] ; ^fAdditionally determined values which were calculated from the same data as that reported before. See ref. [3] ; ^gData obtained from additional extraction experiments. Experimental conditions and data analyses are essentially the same as those reported on ref. [3] . For only the data no. 2, the w phases were prepared with about 0.1 mol dm⁻³ HNO₃.

^*.

^{* §}.

Also, we estimated Df_eq,av from Equation (6) with Equation (5), where Df_eq,av denotes an average value for each run.

The both values, expressed as & in Table 2(b), agreed well within experimental errors.

Average I values of the extraction systems in Table 2(a) were 0.0036 mol×dm⁻³ for the no. 1A [3] , 0.0028 for 1B, 0.0027 for 1C and 0.097 for 2; I denotes the ionic strength of the water phase in the extraction. Except for the data no. 2, we can handle other three data on the average, because experimental conditions [3] of the data are essentially the same (see the footnote g in Table 2(a) for no. 2). So the following values were obtained at 298 K and L = B18C6: logK_ex± = 0.3₁ ± 0.1₄ and logK_D,Pic = −2.54 ± 0.07;

in the I_DCE range of (0.40 - 1.1) ´ 10^-5 mol×dm⁻³ (see the data in Table 2(a)) and

in the same I_DCE range. The symbol, I_DCE, refers to the average ionic strength of the DCE phase; the same is true of I_NB (see Table 3).

Table 3(a) summarizes the fundamental data [7] for the extraction of MPic₂ (M = Ca, Sr & Ba) by 18C6 and B18C6 into NB.

The Df_eq values were calculated from Equation (4) with the logK_D,Pic values in Table 3(a) and the

[11] ones reported previously. From Equation (6) with Equation (10), the

Df_eq,av values were estimated in the same manner. The above findings are listed in Table 3(b).

For the 18C6 extraction systems, the values obtained from Equation (4) are close to the ones from Equation (6) with Equation (10). On the other hand, the former values are larger than the latter ones for the B18C6 extraction systems.

Except for the and values of the B18C6 systems, the above results indicate that the interfa-

cial equilibrium-potential differences, Df_eq, based on Equation (4) are essentially the same as those based on

Equation (6). The differences between and for the B18C6 systems can be due to those in the

charge balance equation between extraction experiments (see Appendix II) and electrochemical (or theoretical)

treatments, namely [7] and Equation (7) or (8). In other words, the condition of cannot be satisfied in the B18C6 systems. For example, an average value of was 0.1₂ for L = B18C6, while that was 0.02₉ for 18C6; these values

were the maximum of the B18C6- and 18C6-M(II) extraction systems. Practically, the values based on Equation (7) or (8) must be more accurate than the ones.

On the basis of the above facts, and, we see that the Df_eq value obtained from the distribution process of is essentially equivalent to that from the combined process of and [8] {see Equations (1) & (2)} or, and {see Equations (7) & (8)} into and NB.

3.2. Experimental Proof of K_ex± and K_ex2± without Df_eq

We obtained the log K_ex± values of the AgPic extraction with B18C6 into DCE from the relation (a) in Table 1 with [9] ([3] ), [11] (into DCE) and the corres

ponding logK_ML,DCE value in Table 2(a). These values, expressed as below, are in good agreement with those listed in Table 2(a).

The K_D,AgL calculation can be an indirect proof of K_ex± without Df_eq. First, the log K_D,AgL values (namely ones) standardized at for L = B18C6 were calculated from the modified form, , of the relation (b) in Table 1. The obtained values are shown as in Table 2(d). In this calculation, we employed [11] (into DCE), [15] (in water), [16] at 298 K.

Next, the logK_D,AgL values were reproduced by using the equation,

at 298 K (see Appendix in ref. [3] for its detailed derivation), with the calculated values and the ones. These values in

Table 2(d) are in good accordance with the values listed in Table 2(a). Thus the log K_D,AgL values can be well

reproduced. From the results of & at least, we can see that Equation (11) is valid for the Ag

Pic-B18C6 extraction system.

Moreover, an average value for all the ones was 1.3₉ ± 0.2₃. From this value and the ones, we calculated the logK_D,AgL values again, using the above relation [3] . The value obtained from of no. 1C was under-estimated by½0.3½ and that of no. 2 was over-estimated by the same, compared to those in Table 2(a) or of. On the other hand, the logK_D,AgL values (= 3.1 & 2.7, respectively) of nos.

1A and 1B were close to those in Table 2(a).

The logK_ex± values for the M(II)-B18C6 extraction into NB were calculated from the relation (c) in Table 1.

These values are in accordance with the values in Table 3(a); the logK_ex± values in Table 3(a) have

been determined by the procedure [2] [7] described in Appendix II. This accordance indicates that Equation (11)

without Df_eq is satisfied. In this calculation, , ,

[10] , logK_CaL,NB = 11.2, logK_SrL,NB = 13.1, logK_BaL,NB = 13.4 for L = 18C6 [17] , logK_CaL,NB = 9.43, logK_SrL,NB = 11.1 and logK_BaL,NB = 11.6 for L = B18C6 [17] were employed. Also, the logK_D,M values were calculated from

the modified form of Equation (3), , with the values, where the values in Table 3(a) corresponding to them were employed accordingly.

The following discussion is similar to that from to K_D,AgL at L = B18C6 (Table 2(d)). The values at M(II) were calculated from a modified form, , of the relation (f) in Table 1. Here, the adopted, in water at 298 K} val-

ues were 0.48 for the Ca-18C6 [18] and -B18C6 [19] systems, 2.72 [20] for Sr-18C6, 3.87 [20] for Ba-18C6, 2.41 [15] for Sr-B18C6 and 2.90 [13] for Ba-B18C6. Also, [11] (into NB), logK_D,18C6 = −1.00 [21] and logK_D,B18C6 = 1.57 [17] (into NB) at 298 K were used for calculation. Furthermore, from the assumption in the section 2.2, we employed the logK_ex2± values [12] which have been reported before and their values virtually correspond to the ones standardized at (see Table 3(a)).

The calculated values are listed in Table 3(d). These values agreed well with those [17] previously-reported by the ion-transfer polarographic measurements, except for the Ba-18C6 and -B18C6 systems. This fact indirectly indicates that Equation (12) is satisfied. For the Ba-18C6 and -B18C6 systems, −2.6 for the former and −0.8 for the latter have been reported [17] .

As similar to in Table 2(d), the calculation of logK_D,ML becomes the indirect proof of logK_ex2±

without Df_eq. Then, the logK_D,ML values at 298 K were estimated from the ones and the equation, [7] ; the values were used here.

The thus-calculated values were close to the values listed in Table 3(a); the experimental

logK_D,ML values in Table 3(a) have been calculated from the relation (d) in Table 1 [7] . This fact indicates that Equation (12) satisfies indirectly the thermodynamic cycle of (f).

^aRef. [7] ; ^bUnit: mol dm⁻³; ^c values: see ref [12] ; ^dValues re-calculated from the data in ref [12] .

^*

^*. ^§.

The above calculation results for the AgPic and MPic₂ extraction with L indicate that the assumption of Equations (11) and (12) without Df_eq is essentially valid. In other words, the overall extraction constants, K_ex± and K_ex2±, must be expressed rationally as functions without Df_eq.

3.3. For Applications to Other Extraction Systems

The above handling based on Table 1 can be also applied to the practical extraction equilibria of

into o = NB [14] , (E11)

into DCE [22] and CH₂Cl₂ [23] , (E12)

into IL = an ionic liquid phase [24] [25] , (E13)

into DCE [26] , (E14)

into NB [27] (E15)

and

into NB [28] . (E16)

As examples, thermodynamic points of view suggest the following cycles for the above equilibria:

(E11c)

(E12c)

(E13c)

(E14c)

with and,

(E15c)

and

(E16c)

with, and, respectively. Similarly, only the K_D,j values are expressed as

functions with the Df_eq ones.

The relation, , for the process (E11) can be arranged into. This does not contradict the fact [14] that the determination of by solvent extraction experiments gives and, when either K_D,M or K_D,A was standardized at which is based on the Ph₄As⁺BPh₄^- assumption [14] [29] & [30] . Also, K_D,C cancels out K_D,A in (E12c):. For and, the value becomes 2.66 ([22] ) and accordingly we have obtained the value at 298 K from the experimental one [11] .

Similarly, K_D,T cancels out K_D,A in (E13c), where T^- denotes another anion. That is,

. For the overall

equilibria, (E14) & (E15), one can handle them in the same manner as that described above for the AgPic and MPic₂ extraction with L, respectively.

We can easily see that the K_D,H and K_D,Pu values cancel out the K_D,Cl one in (E16c). That is,

equals and then becomes . We found the value { = 0.035 V [29] at 298 K}, but were not able to find the value in references.

4. Conclusion

It was demonstrated that the Df_eq values calculated from the experimental logK_D,Pic ones are in agreement with or close to those more-accurately done from the charge balance equations for the species with M(I) in the DCE phase and with M(II) in the NB one, except for some cases. This demonstration indicates that the plots of versus, described in Appendix II with & 2, yield the practical K_D,A

values and then the first-approximated Df_eq ones. These results will give an answer to how one explain the differences in K_D,A among extraction experiments of various MA or MA₂ by various L. Also, we clarified that the assumption of Equations (11) and (12) is valid for the AgPic and MPic₂ extraction with 18C6 and/or B18C6. This eliminated the contradictions [3] [7] due to Df_eq from the thermodynamic cycles. Moreover, the present work indicates a possibility that the proposed handling can be applied to various extraction systems with neutral ligands at least.

Acknowledgements

The authors thank Mr. Tomohiro Amano, Mr. Satoshi Ikeda and Mr. Yuki Ohsawa for their experimental assistances.

Cite this paper

Yoshihiro Kudo, Shoichi Katsuta,, (2015) On an Expression of Extraction Constants without the Interfacial Equilibrium-Potential Differences for the Extraction of Univalent and Divalent Metal Picrates by Crown Ethers into 1,2-Dichloroethane and Nitrobenzene. American Journal of Analytical Chemistry, 06, 350-363. doi: 10.4236/ajac.2015.64034

References

Appendix I

The basic extraction model [1] [3] [31] for the case (i) is as follows.

(corresponding equilibrium constant is K_ML), (A1)

(K₁), (A2)

(K_D,MLA), (A3)

, (A4)

(A5)

and

(K_MA). (A6)

Consequently, these component equilibria yield those of (K_D,M), (K_D,ML), (K_D,L) and (K_D,A). An extraction of HPic, (K_ex,HPic), was added in the

[Pic^-] calculation. The distribution [31] of into the DCE phase was neglected in this study; its constant was not available from references.

The case (ii) [2] [6] [7] was

(K_ML), (A7)

(K₁), (A8)

(K₂), (A9)

(K_D,MLA2), (A10)

, (A11)

, (A12)

(A13)

and

(K_MA+), (A14)

where the distribution of into the NB phase was neglected; their constants were not available from references. Similarly, some equilibria, such as (K_D,M), (K_D,ML) and, can be given from the above component equilibria and the K_ex,HPic value was included in the calculation.

The both models, (i) & (ii), do not contain supporting electrolytes in the o phases. This point is a large difference from corresponding electrochemical measurements [29] [30] .

Appendix II

The K_D,A values have been determined extraction-experimentally using the following equations [1] -[3] [6] [7] .

(A15)

(A16)

for at (the case of M⁺) or for at (that of M²⁺). Hence, the plots of

versus [1] [3] and versus [2] [6] [7] based on Equation (A16)

give the K_D,A value with the K_ex ones for the MA- and MA₂-L extraction systems, respectively. Here, the

values are determined by AAS measurements and then the [M^z+], [L]_o and [A⁻] values are

calculated by a successive approximation [1] -[3] [6] [7] . The following mass-balance equations have been

employed for the approximation: [1] [3] against Equation (1) and [2]

[6] [7] against Equation (7) (see the Section 3.1).

Similarly, the K_ex± values have been evaluated from the other arranged form of Equation (A15),

(A17)

for at or for 1, 2 at 2 [3] [7] .

NOTES

^*Corresponding author.