American Journal of Analytical Chemistry
Vol. 3 No. 12A (2012) , Article ID: 26174 , 7 pages DOI:10.4236/ajac.2012.312A124
A Simplified Method to Estimate the Time Evolution of Oil Extraction from Different Substrates by Supercritical CO2
Dipartimento di Scienze Agrarie, Alimentari e Agro-Ambientali Via del Borghetto, Pisa, Italia
Email: *gandrich@agr.unipi.it
Received October 19, 2012; revised November 26, 2012; accepted December 2, 2012
Keywords: SFE; Food Grade Oils; Sc-CO2; Microalgae; Seeds; Mathematical Model
ABSTRACT
To allow an easy individuation of the more suitable working conditions (temperature, pressure, flow rate, etc.) to be adopted to carry out the extraction of food grade oils from different substrates by supercritical CO2 (Sc-CO2), a simplified kinetic approach has been introduced. This kinetic model was utilised to describe supercritical fluid extraction (SFE) of oil by Sc-CO2 not only from seeds (sunflower, soybean and rape) but also from microalgae (Nannochloropsis sp., Schizochytrium sp. and Spirulina (Arthrospira) platensis) characterised by a lipid fraction with a high proportion of polyunsatured fatty acids (C20:5w-3; C22:6w-3; C18:3w-6). Thanks to the high affinity occurring between oil and Sc-CO2 it was possible to introduce a simplified kinetic model able to describe the time evolution of oil extraction from substrates which deeply differ for biochemical and biophysical characteristics. Moreover the synergistic utilisation of the kinetic model introduced and of the Chrastil’s equation, allowed to predict the time evolution of oil extraction as a function of the: substrate used; amount of its fat content; mass of substrate charged inside the extractor; possible pretreatments carried out on the used substrate; flow rate of Sc-CO2; working conditions adopted (temperature, pressure and then Sc-CO2 density).
1. Introduction
Nowadays supercritical fluid extraction (SFE) represents an industrial process used to produce decaffeinated coffee beans, hop extracts, antioxidants, spices, nutraceuticals and others. Although oil extraction using organic solvent is normally recognised as a highly developed technology, research is in progress to find new solvents which are safer than traditional solvent used (hexane) and which offer higher quality final products, above all from a toxicological point of view. Among the alternative solvents proposed, supercritical CO2 (Sc-CO2) has been investigated for three microalgae (Nannochloropsis sp., Schizochytrium sp. and Spirulina (Arthrospira) platensis) [1-3] and for three oilseeds (sunflower, rape and soybean) [4-6].
In particular Sc-CO2, being safer than hexane and offering a negligible environmental impact, a short extraction time and a petroleum-free final product is regarded with an increasing interest for oil extraction from microalgae, which are recognised as an important renewable source of bioactive lipids. In fact, clinical and epidemiological studies have shown that long-chain polyunsatured fatty acids (LC-PUFA) are effective in preventing or treating several diseases and that the current diet of the economically advanced countries does not adequately cover their requirement. Marine fish lipids are the main conventional source of LC-PUFA, but microalgae are recognised as an additional important source (Table 1).
When compared to fishery and related food industries, microalgal cultivation presents the advantage to use an indefinitely renewable resource with a negligible environmental impact. Moreover, the growth of microalgae in batch or in photo-bioreactor is carried out under highly controlled conditions allowing the production of uncontaminated strains having a standardised composition.
In such a context, to better analyse the experimental results obtained and to optimize the working variables (temperature, pressure, etc.), this extractive technology could greatly benefit mathematical models not only suitable and reliable but also easy as possible to use.
Different phenomena as phase equilibrium, mass transfer and flow of Sc-CO2 trough packed bed are differently involved in the kinetic models reported in literature [7,8].
But in many cases, the extraction of the first fraction of extract is essentially limited by its solubility while only the extraction rate of the remaining fraction is limited by internal diffusion trough the utilised matrix [9].
As CO2 is able to dissolve non polar substances like vegetable oil, this largely prevails in microalgae and oilseeds extracts so that extracts can be identified with the only oil and the mathematical model can simulate the solute as one (pseudo) component (oil) instead of a complex mixture [10-13].
On these basis a simplified mathematical model was introduced to describe the time evolution of SFE of lipid fraction from oilseeds [4-6] and microalgae [1-3]. By Chrastil’s equation [14] it was also possible to correlate the maximum extraction rate with the working pressure and temperature adopted.
As a function of temperature, pressure, flow-rate of Sc-CO2 and amount of matrix experimentally used, a simplified method to estimate the time evolution of oil extraction by Sc-CO2 from the three oilseeds (sunflower, soybean and rape) and the three microalgae (Nannochloropsis sp., Schizochytrium sp. and Spirulina (Arthrospira) platensis) analysed, could be now developed. This new method could be potentially able to simplify the identification of the best working conditions to be adopted to promote SFE of oil from these six matrices and to reduce the weight of the related experimental activity.
2. Materials and Methods
SFEs were performed with commercial-grade CO2 using a pilot plant apparatus (SITEC, Maur, Switzerland) described in a previous paper [15].
Different amounts (180 g for Nannochloropsis and 80 g for Schizochytrium and Spirulina) of lyophilised microalga (particle size £ 0.37 mm) were utilised per each run, with a working pressure (P) of 25, 40, 55, 70 MPa and a temperature (T) of 40˚C, 55˚C. The oil of the three microalgae used (24.9% by weight for Nannochloropsis, 36.2% for Schizochytrium and 7.9% for Spirulina) was extracted by Soxhlet using n-hexane as solvent.
Sunflower, rape and soybean seeds were cracked, dehulled and flaked to produce flakes with a thickness of 0.2 - 0.5 mm. Moisture and oil content of the flakes, determined according to standard AOCS methods, resulted respectively 7.0% (by weight) and 40.8% for sunflower, 8.8% and 41.0% for rape and 9.6% and 20.2% for soybean, ScCO2 extractions of oil were carried out using 280 g of flakes per each run, with a working pressure (P) of 20, 30, 40, 50, 55, 70 MPa and a temperature (T) of 40˚C, 50˚C, 60˚C, 70˚C, 80˚C.
In all experimental runs the flow rate of Sc-CO2 (F) was maintained constant and equal to 10 kg×h−1 (Micro Motion Coriolis flow-meter; accuracy ±0.2%; repeatability ±0.05%).
The extracted lipid fractions were collected after a predetermined amount of CO2 had passed through the bed of used substrate (lyophilised microalgae or seeds flakes) and the extraction yields were determined gravimetrically.
3. Results and Discussion
3.1. Kinetic Evaluation of Oil Extraction
Applying the Fick’s law to the diffusion occurring between two heterogeneous phases (solid matrix and ScCO2), the rate (d[Oe]t=t/dt) of oil accumulation in the mobile phase (Sc-CO2) was assumed to be proportional to the difference occurring between the concentration of oil ([Oe*]t=t ), which would be present in this phase at the equilibrium, with the amount of oil remained inside the solid matrix ([Os]t=t; [Oe*]t=t = H∙[Os]t=t), and the concentration of oil already extracted at that run time ([Oe]t=t) and the following equation could be obtained [1-6]:
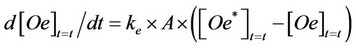 (1)
(1)
where:
ke = mass transfer constant (s−1∙ m−2);
A = area of contact between the two phases: solid matrix and Sc-CO2 (m2);
H = the equilibrium constant H, related to the partition of oil between the two involved phases 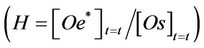
The differential Equation 1 could be integrated, adopting some simplifying hypothesis [1,5] and utilising the equation related to mass balance of oil between the two involved phases:
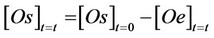 (2)
(2)
where: [Os]t=t = the amount of oil still present in the solid phase; [Os]t=0 = oil concentration initially present in the solid matrix used; [Oe]t=t = concentration of oil already

Table 1. Major characteristics of microalgae used.
extracted in the mobile phase.
And Equations 3 and 4 could be obtained:
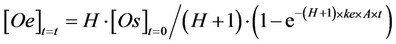 (3)
(3)
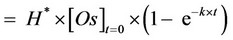 (4)
(4)
where: [Oe] = amount (g) of oil extracted at a random time t = t per gram of solid matrix used in the SFE; H* = adimensional constant, ranging from 0 to 1, related to the equilibrium constant H (H* = H/(H + 1)); [Os]t=0 = amount (g) of oil present in 1 g of starting material; k = (H + 1)×ke×A = kinetic constant (s−1).
The extraction rate (R) calculated as first derivative of the exponential Equation 5:
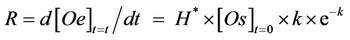 (5)
(5)
reaches its maximum value (Rmax) at the beginning of extraction, when t is close to 0:
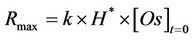 (6)
(6)
According to Yu et al. [16], the value of Rmax (s−1) was assumed as an index to evaluate the efficiency of the SFE system versus the oil fraction of the oily matrix used. In particular, while the constant k gives information on the kinetics of the SFE, the product H*×[Os], which represssents the asymptotic value of the extraction curve when t®¥, measures the maximum amount of oil extractable in the working conditions adopted.
The identification of the best values to be assigned to the equation parameters H*×[Os] and k was carried out by a commercial statistical program (BURENLÓ), which is able to identify in a space of j-dimensions (where j is the number of equation parameters) the minimum of the function F which is given by the sum of the squares of differences occurring between calculated (Vcalc.,i) and experimental (Vexper.,i) values:
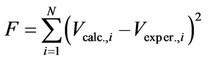 (7)
(7)
where N is the total number of experimental points. Table 2 reports the values assumed by Rmax and by the functional parameters H*×[Os] and k for the three microalgae (Nannochloropsis, Schizochytrium and Spirulina) and the three oilseeds (sunflower, rape and soybean) used.
The high values assumed by the square of correlation coefficients, testify to the suitability of the hypotheses introduced and give a measure of the validity of the theoretical approach followed.
The values assumed by the constant k, when working in isothermal conditions, reveal that the kinetics of SFE is influenced by pressure, with the strongest effect obtained working with Spirulina platensis and sunflower flakes. In particular, when passing from 25 to 70 MPa, the value of k increases of about 10 times at 40˚C and more than 20 times at 55˚C for Spirulina platensis, while a comparable increase can be observed also for sunflower flakes at 40˚C, which becomes equal to 45 times at 60˚C and to 290 at 80˚C.
Also temperature affects the kinetics of SFE (see values of k determined in isobaric conditions), but such influence appears more complex as shown by curves reported in Figures 1 and 2 for microalgae and oilseeds respectively.
At the lower pressures, in fact, T plays a negative effect on the extraction kinetics, while at the higher P values an isobaric increase in T, increases the value of k. The crossing-over region ranges from 33 to 46 MPa. Such phenomenon, supported by a number of experimental studies, is related to the fact that at the lower pressures the expected increase in oil fugacity with the increase of T is overcome by the decrease in density of Sc-CO2 and therefore by the decrease in its solute holding power.
As already reported in literature Sc-CO2 is confirmed as a good solvent for oil extraction from all the substrates tested as shown by values assumed by equation parameter H*×[Os]t=0 and reported in Table 2.
Within each set of SFEs, the equation parameter H*×[Os]t=0 assumes very similar values, which are also close to that obtained when n-hexane is adopted as solvent. Table 3 reports the mean values calculated for every SFE set together with the corresponding solubility found using n-hexane as extraction solvent.
This means that on the basis of the amount of oil extractable at equilibrium, all processes (Sc-CO2 extractions and percolation with n-hexane) are substantially equivalent. This result disagrees with that reported by Mendes et al. for the SFE of oil from Spirulina (Arthrospira) maxima [17]. Such Authors report in fact a higher extraction yield when working with n-hexane instead ScCO2, albeit SFE was carried out under different working conditions. Comparing the values of H*×[Os] with the oil content reported in Table 1 for each microalga, it appears that ScCO2 and n-hexane are unable to recover the whole microalgal oil fraction, having probably some losses in the most polar lipids (e.g. glycolipids).
The functional parameter (H*×[Os]t=0), representing the mgs of oil extracted from 1 g of matrix initially charged inside the extractor when extraction time tends to infinite, appears to assumes for all materials tested and experimental runs performed (Table 3), values coinciding with the concentrations of oil extractable from different matrices by solvent usually utilised in the industrial oil productions.
In fact, in the presence of a highly efficient SFE process (high affinity of extractable substance for solvent and then for Sc-CO2) H* tends to 1:
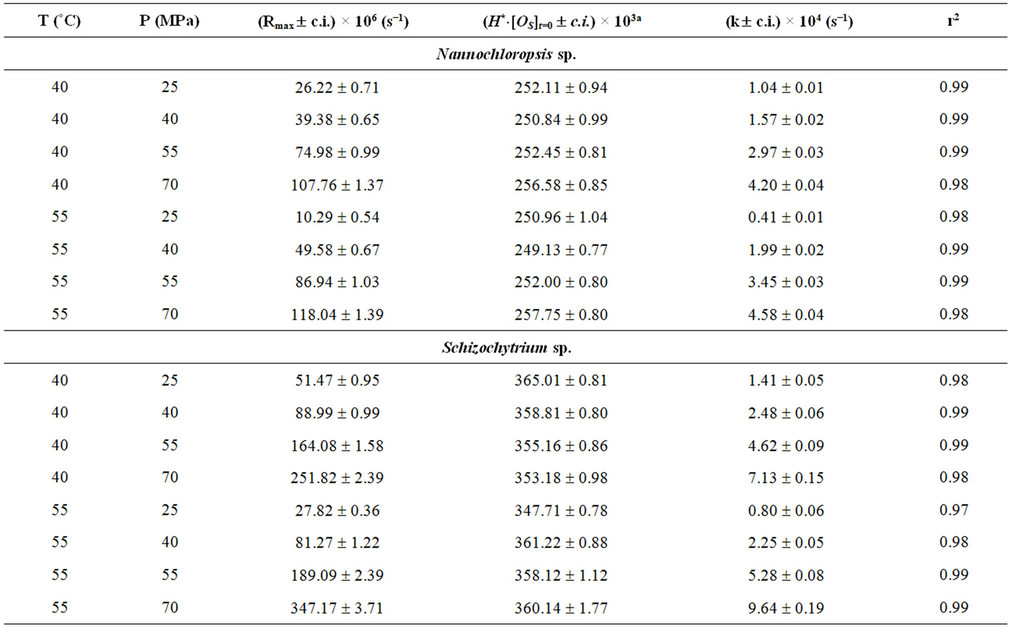


Table 2. Maximum extraction rate (Rmax) and values of the equation parameters H*×[Os]t=0 and k as a function of temperature (T) and pressure (P) adopted during the experimental runs related to SFEs of the three microalgae (Nannochloropsis, Schizochytrium and Spirulina) and the three oilseeds (sunflower, rape and soybean) used. c.i. = confidence interval ( p = 0.05); r2 = the square of correlation coefficient.

Table 3. Mean values assumed by equation parameter H*×[Os]t=0 determined for every substrate used together with their related confidence intervals (c.i.; p = 0.05) and corresponding solubility determined utilising n-hexane as extraction solvent.
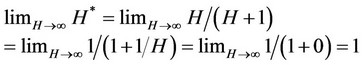
so that the maximum amount of oil extractable per gram of biomass becomes completely comparable with the concentration of oil present in the starting material and a simplified kinetic model can be introduced [9,13].
To relate Rmax to density of Sc-CO2, whose value is influenced by both the pressure and temperature adopted,
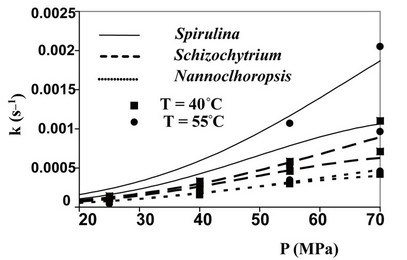
Figure 1. Evolution of kinetic constant k as a function of microalga, pressure and temperature utilised.
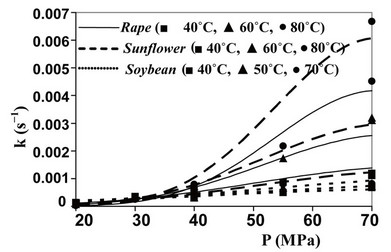
Figure 2. Evolution of kinetic constant k as a function of oilseed, pressure and temperature utilised.
the following equation introduced by Chrastil was adopted:
![]() (8)
(8)
where: R*max = the maximum value assumed by extraction rate expressed in grams of extracted oil per litre of Sc-CO2 flowed through the substrate bed (g/L); Rmax = the maximum value of extraction rate (s−1); m = the amount of substrate used (g); r = density of Sc-CO2 (g×l−1); F = flow rate of Sc-CO2 (g×s−1); a, b (K), c = equation parameters; T = temperature (K). The identification of the best values to be assigned to the equation parameters a, b and c was carried out by the statistical program BURENLÓ introduced above Table 4 reports the value of the parameters a, b and c calculated for every substrates tested, using the experimental values of Rmax reported in Table 2.
The high values assumed by the square of correlation coefficients give a measure of the validity of Chrastil’s equation to describe the evolution of the maximum extraction rate as a function of temperature and pressure utilised. Known for the six substrates tested the values assumed by the three functional parameters (a, b and c) and the working temperature and pressure used, it is possible to calculate the corresponding R*max value and then that of kinetic constant k. In fact combining Equation 6 with 8, the following expression can be obtained:
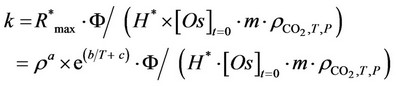 (9)
(9)
The value of density assumed by Sc-CO2  as a function of temperature and pressure adopted, can be evaluated looking to the state diagram of carbon dioxide. So it was possible to calculate the theoretic evolutions of the kinetic constant k connected to SFE of oil from the six substrates studied by Sc-CO2 as a function of temperature and pressure used (Figures 1 and 2). The good
as a function of temperature and pressure adopted, can be evaluated looking to the state diagram of carbon dioxide. So it was possible to calculate the theoretic evolutions of the kinetic constant k connected to SFE of oil from the six substrates studied by Sc-CO2 as a function of temperature and pressure used (Figures 1 and 2). The good
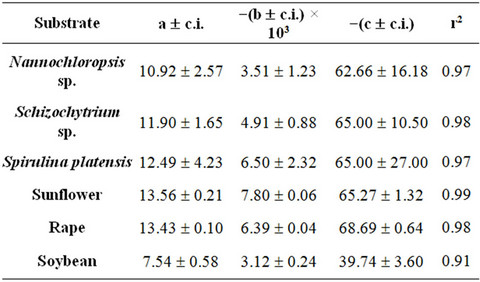
Table 4. Values of parameters involved in the Chrastil equation 11 adopted to correlate the solvent power of ScCO2 to its density and working temperature utilised. c.i. = confidence interval (p = 0.05); r2 = square of correlation coefficient.
degree of overlapping occurring between experimental and calculated values gives a measure of the suitability of the method introduced.
Moreover the values assumed by kinetic constant (k) when the SFE of sunflower is carried out at a pressure of 50 Mpa of Sc-CO2 and at three different temperatures (40˚C, 60˚C and 80˚C) were also determined (Table 5) when 280 g of sunflower flakes is charged inside the extractor and a flow rate of Sc-CO2 equal to 2.78 (g∙s−1) is utilised.
Figure 3 reports the time evolution of oil extraction calculated by Equation 7 and utilising the values of functional parameters reported in Table 5.
The good degree of overlapping between the calculated and experimental curves (Figure 3) and the high values assumed by the squares of correlation coefficients occurring between experimental and calculated values (0.95 at T = 40˚, 0.96 at T = 60˚ and T = 80˚C) seem to testify to the suitability of the hypotheses introduced and give a measure of the validity of the theoretical approach followed.
Thanks to the high affinity occurring between oil and Sc-CO2 it was possible to introduce a simplified kinetic model able to describe the time evolution of oil extraction from substrates which deeply differ for biochemical and biophysical characteristics. Moreover the synergistic utilisation of this simplified kinetic model together with the Chrastil’s equation allowed to predict the time evo-
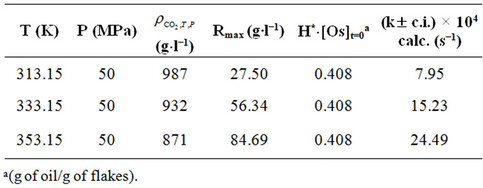
Table 5. Values calculated for the kinetic constant (k) by Chrastil’s equation and related to oil extraction from sunflower flakes at pressure of 50 MPa of Sc-CO2 at three different temperatures (40˚C, 60˚C and 80˚C).
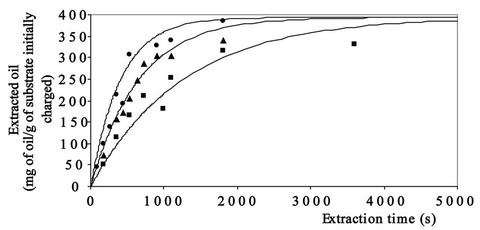
Figure 3. Evolution of experimental and calculated points related to oil extraction from sunflower flakes as a function of time, pressure (50 MPa) and temperature (■ 40˚C, ▲ 60˚C and ● 80˚C) utilised.
lution of oil extraction as a function of the: substrate used;amount of its fat content; mass of substrate charged inside the extractor; possible pretreatments carried out on the used substrate; flow rate of Sc-CO2; working conditions adopted (temperature, pressure and then Sc-CO2 density).
This new method could be potentially able to simplify the identification of the best working conditions to be adopted to promote SFE of oil from matrices of which are known the values assumed by functional parameters (a, b and c) involved in the of Chrastil’s equation.
REFERENCES
- G. Andrich, U. Nesti, F. Venturi, A. Zinnai and R. Fiorentini, “Supercritical Fluid Extraction of Bioactive Lipids from Microalga Nannochloropsis sp.,” European Journal of Lipid Science and Technology, Vol. 107, No. 6, 2005, pp. 381-386. doi:10.1002/ejlt.200501130
- G. Andrich, A. Zinnai, U. Nesti, F. Venturi and R. Fiorentini, “Supercritical Fluid Extraction of Oil from Microalga (Arthrospira) platensis,” Acta Alimentaria, Vol. 35, No. 2, 2006, pp. 195-203. doi:10.1556/AAlim.35.2006.2.6
- A. Zinnai, U. Nesti, F. Venturi, G. Andrich and R. Fiorentini, “Estrazione in Fase Supercritica di Olio da Schizochytrium sp.,” Rivista Italiana Delle Sostanze Grasse, Vol. 83, No. 1, 2006, pp. 1-5.
- G. Andrich, S. Balzini, A. Zinnai, V. De Vitis, S. Silvestri, F. Venturi and R. Fiorentini, “Supercritical Fluid Extraction in Sunflower Seed Technology,” European Journal of Lipid Science and Technology, Vol. 103, No. 3, 2001, pp. 151-157. doi:10.1002/1438-9312(200103)103:3<151::AID-EJLT151>3.0.CO;2-T
- G. Andrich, A. Zinnai, S. Nottoli , F. Venturi and R. Fiorentini, “A Mathematical Model Describing the Supercritical Fluid Extraction (SFE) of Oil from Soybean Seeds,” Chemical Engineering Transactions, Vol. 2, 2002, pp. 397-401.
- G. Andrich, A. Zinnai, F. Venturi and R. Fiorentini, “A Mathematical Model Describing the Supercritical Fluid Extraction (SFE) of Rapeseed (Brassica Napus) Oil,” Chemical Engineering Transactions, Vol. 3, 2003, pp. 1605-1610.
- J. M. Del Valle and J. C. De La Fuente, “Supercritical CO2 Extraction of Oilseeds: Review of Kinetic and Equilibrium Models,” Critical Reviews in Food Science and Nutrition, Vol. 46, No. 2, 2006, pp. 131-160. doi:10.1080/10408390500526514
- E. L. G. Oliveira, A. J. D. Silvestre and C. M. Silva, “Review of Kinetic Models for Supercritical Fluid Extraction,” Chemical Engineering Research and Design, Vol. 89, No. 7, 2011, pp. 1104-1117. doi:10.1016/j.cherd.2010.10.025
- H. Sovová, “Steps of Supercritical Fluid Extraction of Natural Products and Their Characteristic Times,” The Journal of Supercritical Fluids, Vol. 66, 2012, pp. 73-79. doi:10.1016/j.supflu.2011.11.004
- I. Zizovic, M. Stamenic, A. Orlovic and D. Skala, “Supercritical Carbon Dioxide Essential Oils from Plants with Secretory Ducts: Mathematical Modelling on the Micro-Scale,” The Journal of Supercritical Fluids, Vol. 39, No. 3, 2007, pp. 338-346. doi:10.1016/j.supflu.2006.03.009
- M. Stamenic, I. Zizovic, A. Orlovic and D. Skala, “Mathematical Modelling of Essential Oil SFE on the Micro-Scale-Classification of Plant Material,” The Journal of Supercritical Fluids, Vol. 46, No. 3, 2008, pp. 285-292. doi:10.1016/j.supflu.2008.03.007
- L. Fiori, D. Basso and P. Costa, “Supercritical Extraction Kinetics of Seed Oil: A New Model Bridging the ‘Broken and Intact Cells’ and the ‘Shrinking-Core’ Models,” The Journal of Supercritical Fluids, Vol. 48, No. 2, 2009, pp. 131-138. doi:10.1016/j.supflu.2008.09.019
- H. Sovová, “Modelling the Supercritical Fluid Extraction of Essential Oil from Plant Materials,” Journal of Chromatography A, Vol. 1250, 2012, pp. 27-33. doi:10.1016/j.chroma.2012.05.014
- J. Chrastil, “Solubility of Solids and Liquids in Supercritical Gases,” Journal of Physical Chemistry, Vol. 86, No. 15, 1982, pp. 3016-3021. doi:10.1021/j100212a041
- F. Favati, R. Fiorentini and V. de Vits, “Supercritical Fluid Extraction of Sunflower Oil: Extraction Dynamics and Process Optimisation,” Proceedings of the 3rd International Symposium on Supercritical Fluids, Strasbourg, 17-19 October 1994, pp. 305-309.
- Z. Yu, B. Sing, S. H. Risvi and J. A. zollweg, “Solubilities of Fatty Acids, Fatty Acid Esters, Triglycerides and Fats and Oils in Supercritical Carbon Dioxide,” Journal of Supercritical Fluids, Vol. 7, No. 1, 1994, pp. 51-59. doi:10.1016/0896-8446(94)90006-X
- R. L. Mendes, A. Reis, H. L. Fernandes, J. M. Novais and A. F. Palavra, “Supercritical CO2 Extraction of Lipids from a GLA-Rich Arthrospira (Spirulina) maxima Biomass,” Proceedings of the 5th Iternational Conference on Supercritical Fluids and Their Applications, Verona, 13- 16 June 1999, pp. 209-216.
NOTES
*Corresponding author.

