Modeling and Numerical Simulation of Material Science
Vol.3 No.4(2013), Article ID:37920,12 pages DOI:10.4236/mnsms.2013.34023
Metal Hexaborides with Sc, Ti or Mn
1Institute for Future Environments, Brisbane, Australia 2Science and Engineering Faculty, School of Chemistry, Physics and Mechanical Engineering, Queensland University of Technology, Brisbane, Australia
Email: ian.mackinnon@qut.edu.au
Copyright © 2013 Ian D. R. Mackinnon et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 20, 2013; revised September 22, 2013; accepted October 10, 2013
Keywords: metal hexaborides; electronic structure; superconductivity; boron framework
ABSTRACT
Comparison of well-determined single crystal data for stoichiometric, or near-stoichiometric, metal hexaborides confirms previously identified lattice parameter trends using powder diffraction. Trends for both divalent and trivalent forms suggest that potential new forms for synthesis include Sc and Mn hexaborides. Density Functional Theory (DFT) calculations for KB6, CaB6, YB6, LaB6, boron octahedral clusters and Sc and Mn forms show that the shapes of bonding orbitals are defined by the boron framework. Inclusion of metal into the boron framework induces a reduction in energy ranging from 1 eV to 6 eV increasing with ionic charge. For metals with d1 character, such a shift in energy brings a doubly degenerate band section along with the G-M reciprocal space direction within the conduction bands tangential to the Fermi surface. ScB6 band structure and density of states calculations show directions and gap characteristics similar to those of YB6 and LaB6. These calculations for ScB6 suggest that it may be possible to realize superconductivity in this compound if synthesized.
1. Introduction
Metal hexaborides, MB6 (where M includes alkali, transition and rare-earth metals) show simple cubic symmetry (Pm m) in which the metal is in 24-fold coordination with a framework of boron octahedra at the vertices of a cube. This boron octahedral framework is a key contributor to the physical properties ascribed to many hexaborides. The isostructural forms of MB6 are superconductors (e.g. M = Y, Th) [1,2], metallic conductors (e.g. M = La, Gd, Dy) [3,4] and semi-conductors (e.g. M = Ca, Sr and Yb) [5,6] while others display intermediate or unusual behavior (e.g. M = Sm, Ce, Nd) [7,8] or have notable thermal stability and hardness [9,10].
m) in which the metal is in 24-fold coordination with a framework of boron octahedra at the vertices of a cube. This boron octahedral framework is a key contributor to the physical properties ascribed to many hexaborides. The isostructural forms of MB6 are superconductors (e.g. M = Y, Th) [1,2], metallic conductors (e.g. M = La, Gd, Dy) [3,4] and semi-conductors (e.g. M = Ca, Sr and Yb) [5,6] while others display intermediate or unusual behavior (e.g. M = Sm, Ce, Nd) [7,8] or have notable thermal stability and hardness [9,10].
In general, metal ions are divalent or trivalent except for KB6 [11,12] and ThB6 [13]. The smaller size metal ion generally does not favor formation of hexaborides for multi-valent elements (e.g. Pr3+ is preferred over Pr4+; Ce3+ over Ce4+). Formation of actinide hexaborides can be enhanced through substitution, for example, in HoB6 using Ca or La as minor substitutents [14]. In general, mixed metal forms of hexaboride such as (Nd1−xGdx)B6, (Ce1−xNdx)B6 or (Ce1−xLax)B6 [15-17] follow Vegard’s law [18] with the exception of SmxM1−xB6 structures. Other exceptions to Vegard’s law across a full substitution range include (EuxCa1−x)B6 for which phase separation occurs at x = 0.27 [19].
Seminal work on hexaborides undertaken prior to the 1970’s is well documented in the volume by Matkovich [20]. In this work, general inferences relating to structures and properties including band structure calculations are presented for CaB6, LaB6 and BaB6 [21]. More recently, high resolution crystal structure determinations of additional hexaboride compositions have been completed (e.g. Sm, Ce, Sr, Ca, Nd, Eu). These carefully defined structures allow further insight into bond length variations and their influence on electronic properties within the hexaboride suite. In this work, we compile and compare these structure determinations of end-member metal hexaborides with other hexaborides that may be formed at stoichiometric, or near stoichiometric composition given the development of facile and chemically precise synthesis methods. While electronic structure calculations have been undertaken for a range of compositions [5,12,21], theoretical studies of Sc, Ti or Mn hexaborides are not extant in the literature and are provided in this work.
2. Experimental Data and Calculation Methods
Data from single crystal refinements and high resolution powder diffraction studies are compiled from the literature. Data from refinements with quality goodness of fit measures (e.g. Rw ≤ 5%) are listed in Table 1 along with reference sources.
Band structure calculations are undertaken using the CASTEP module of the Materials Studio 6.1 software package. Details of this software and the CASTEP module are well described [22]. Most calculations have been performed using the Local Density Approximation (LDA). For comparison, some calculations have also been performed in the Generalized Gradient Approximation (GGA). The LDA is exact in the uniform electron density limit and the GGA includes information on the spatial variations in electron density, using functions which are only valid for slowly varying densities [23]. A well established outcome of previous work is that LDA calculations yield bonds shorter than experimental values and GGA models estimate longer bonds than experimental. Further details on model assumptions and outcomes are available at Milman et al. [24].
Initial structures are normally optimized for geometry and all calculations make use of plane-wave (PW) basis, linear response functions, norm-conserving pseudo potentials and interpolation methods. The PW basis set cut-off is typically >290 eV and the energy cut off is 10 eV. For the same metal hexaboride, some calculations are undertaken with different optimized cell parameters in order to explore the limits of structure stability.
3. Crystal Structure
Metal hexaborides are cubic structures with an ambiguous bonding character that is, on the one hand, considered ionic and, on the other, covalent or hybrid bonded, particularly within the boron framework. Indeed, recent ab initio calculations on the LaB6 electronic structure show that covalent, metallic and ionic bonding co-exist in this specific structure [25]. Ionic character seems predominantly related to M2+ valences with the third electron in M3+ ions participating in metallic conduction bands. Structure refinements of alkali, alkali-earth, rare earth and actinide hexaborides support the concept of a boron framework within which metal ions are vibrating freely in the interstitial positions [6,8,13,17,26]. In general, the refined temperature factors for boron are anisotropic and reflect the strengths of the inter-octahedral bond relative to the intra-octahedral bond [17]. For the rare earth hexaborides, structure refinements confirm that vacancies occur on the boron site [8,13,17,27]. Boron isotopic effects are also manifest in the symmetry and frequency of Raman vibrations [9].
MB6 structures have two different boron-boron bond lengths: the inter-octahedral and the intra-octahedral as shown in Figure 1. The intra-octahedral B-B bond (BBin in this study) is longer than the inter-octahedral bond (B-Bout in this study). The shorter length of the in-
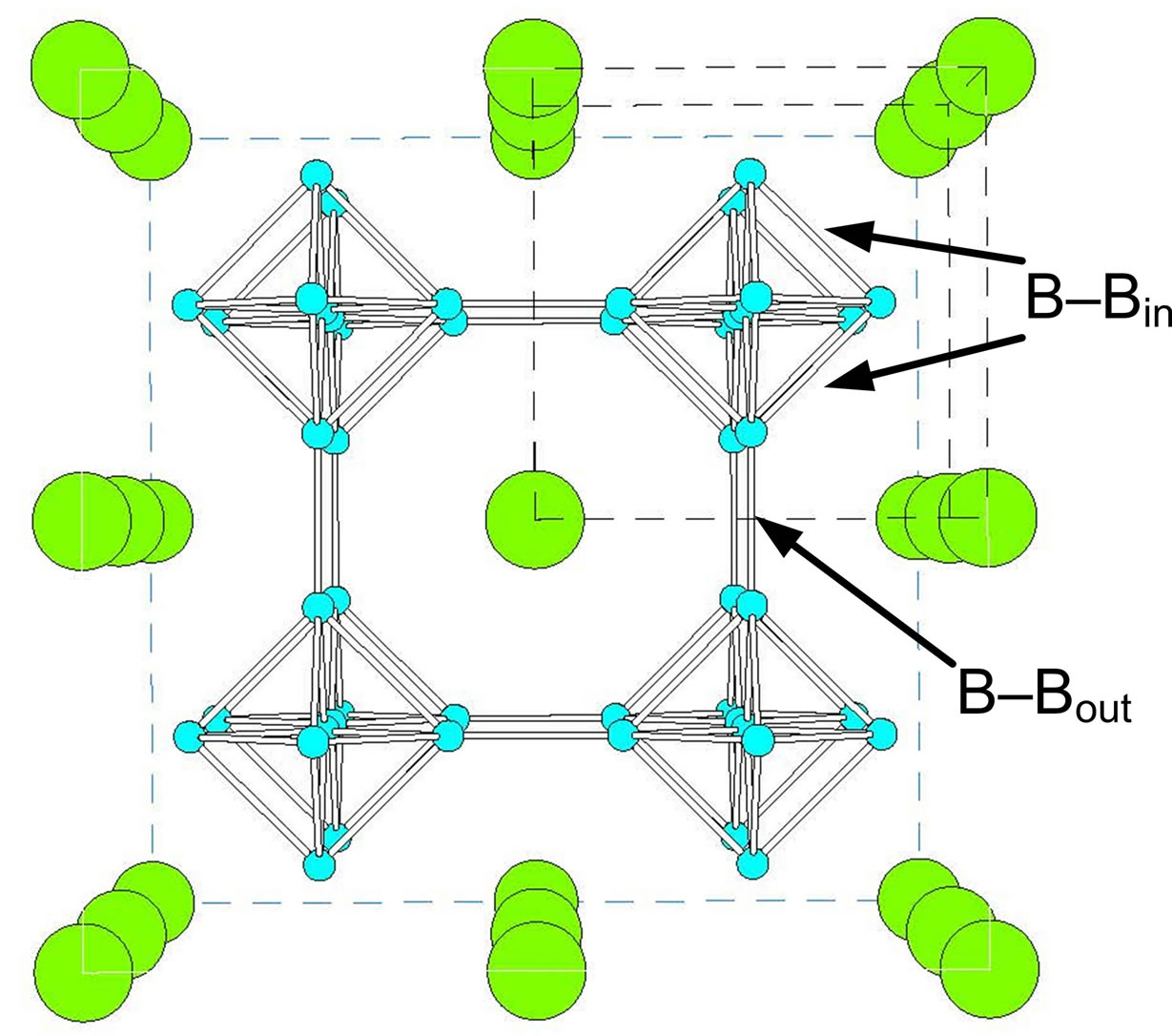
Figure 1. Perspective view of MB6 structure looking down [100]; M atoms are the larger green spheres; boron atoms are the smaller blue spheres.
ter-octahedral bond influences thermal stability and hardness of hexaborides among a number of properties [10].
3.1. Cell Dimensions
Of the nineteen end-member hexaborides synthesized to date, eleven have been subjected to high resolution powder diffraction or single crystal structure refinements. Data for these structure determinations have been collected at ambient or room temperature. The detailed reports on SmB6 and CeB6 single crystals at a range of temperatures (100 K, 165 K, 230 K and 298 K) are exceptions [28,29] and provide key evidence for donation of 4f electrons to the B-B bonds connecting B6 octahedra in these structures. XRD studies on slightly K-deficient KB6 have shown indications of lattice instabilities at 60K [12]. The lack of low temperature structural data for a broader range of hexaborides indicates that key phenomena are likely waiting to be discovered.
Data on end-member hexaborides for which compositions have been independently assessed or estimated from structure refinements are listed in Table 1. Table 1 lists data with a weighted residual (Rw) based on least squares refinement of structure factors that provides a measure of refinement precision. The high symmetry of MB6 provides few crystallographic parameters to describe, or refine, a structure. Two primary parameters are the cell dimension, a, and z, the 6f position for boron at the (1/2, 1/2, z) site.
Ionic radii listed in Table 1 are for eight-fold coordination of the lowest charge form of the metal. The calculated parameter, a-2rR [30], is listed in Table 1 because for hexaborides the mean square displacements of rare earth metal ions appear to correlate with a-2rR [31], where rR is the ionic radius for the respective metal ion. The data by Chernyshov et al. [31] when recalculated, reflect ionic radii for the metal ion in six-fold coordination. As noted below, experimental data show that specific metal ions prefer certain geometric configuration(s)
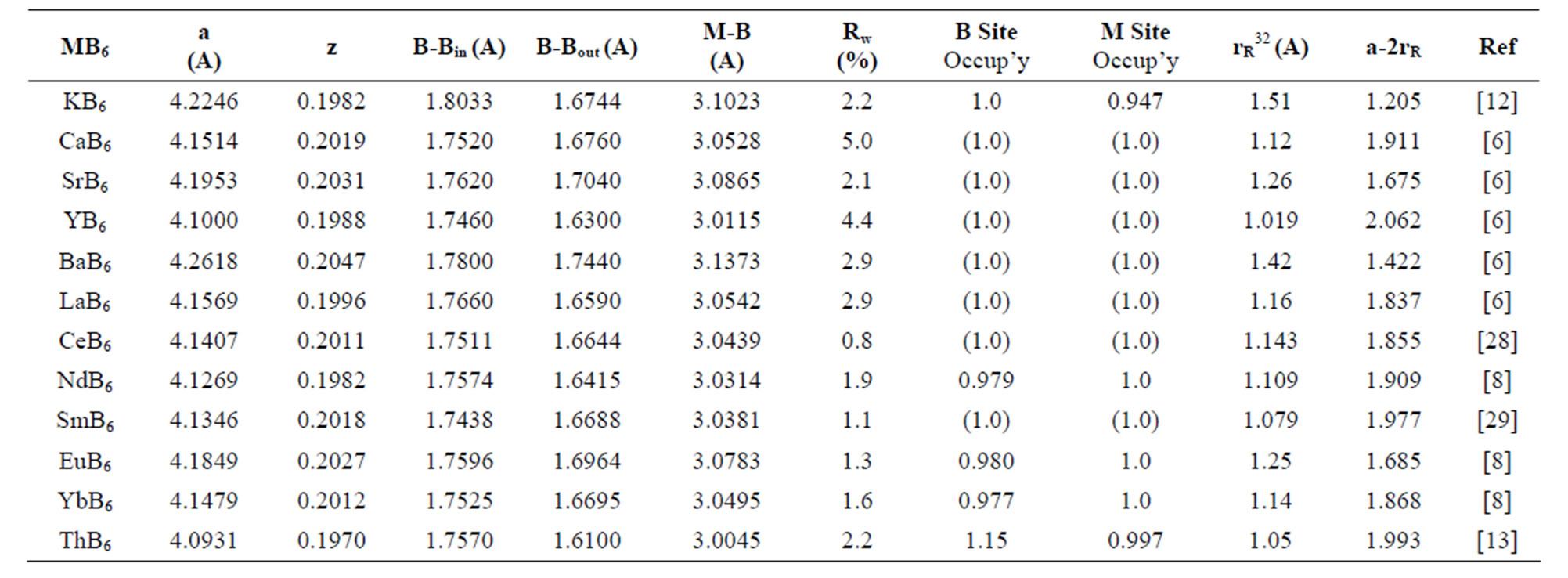
Table 1. Summary of experimental structural parameters for metal hexaborides.
and, in order to correct the record, Table 1 lists calculated values for a-2rR for metal ions in eight-fold coordination. Eight-fold coordination is a more reasonable expectation for metal ion coordination given eight vertices in a cube.
For nineteen refined cell dimensions evaluated, including those in Table 1, the variation in values is less than 5% while the variation in ionic radii for metals of the same structures is many times at 30% - 40%. Yahia et al. [9] suggest this feature is a clear indication of the rigidity of the boron lattice. However, the boron framework accommodates a wide range of valence electron distributions despite the constraints of high symmetry.
Figure 2 shows a plot of cell parameter, a, against ionic radius [32] for a range of MB6 structures containing divalent or trivalent metal ions listed in Table 1. The calculated systematic errors for each lattice parameter are contained within the symbols in Figure 2. These data show an expected linear relationship between cell dimension and ionic radius for six-fold and for eight-fold coordinated divalent or trivalent metal ions in the MB6 structure. Both trends—using only structure determinations for divalent or trivalent metal hexaborides (blue filled symbols in Figure 2)—show a strong linear correlation for six-fold and eight-fold coordination (r2 = 0.97 and 0.98, respectively) with slightly better alignment of the Th lattice parameter in eight-fold coordination. Both K and Th are not included in the least squares linear fits shown in Figure 2. Superconducting hexaborides are denoted with a red-outline to the symbol in Figure 2. Unfilled symbols in Figure 2 are for potential structures for which a cell dimension has been estimated using the respective linear trend.
However, KB6 does not lie on this linear trend for either coordination as indicated in Figure 2. Note that the value for K in six-fold coordination plots close to the trend line for eight-fold coordination. Similarly, if twel-
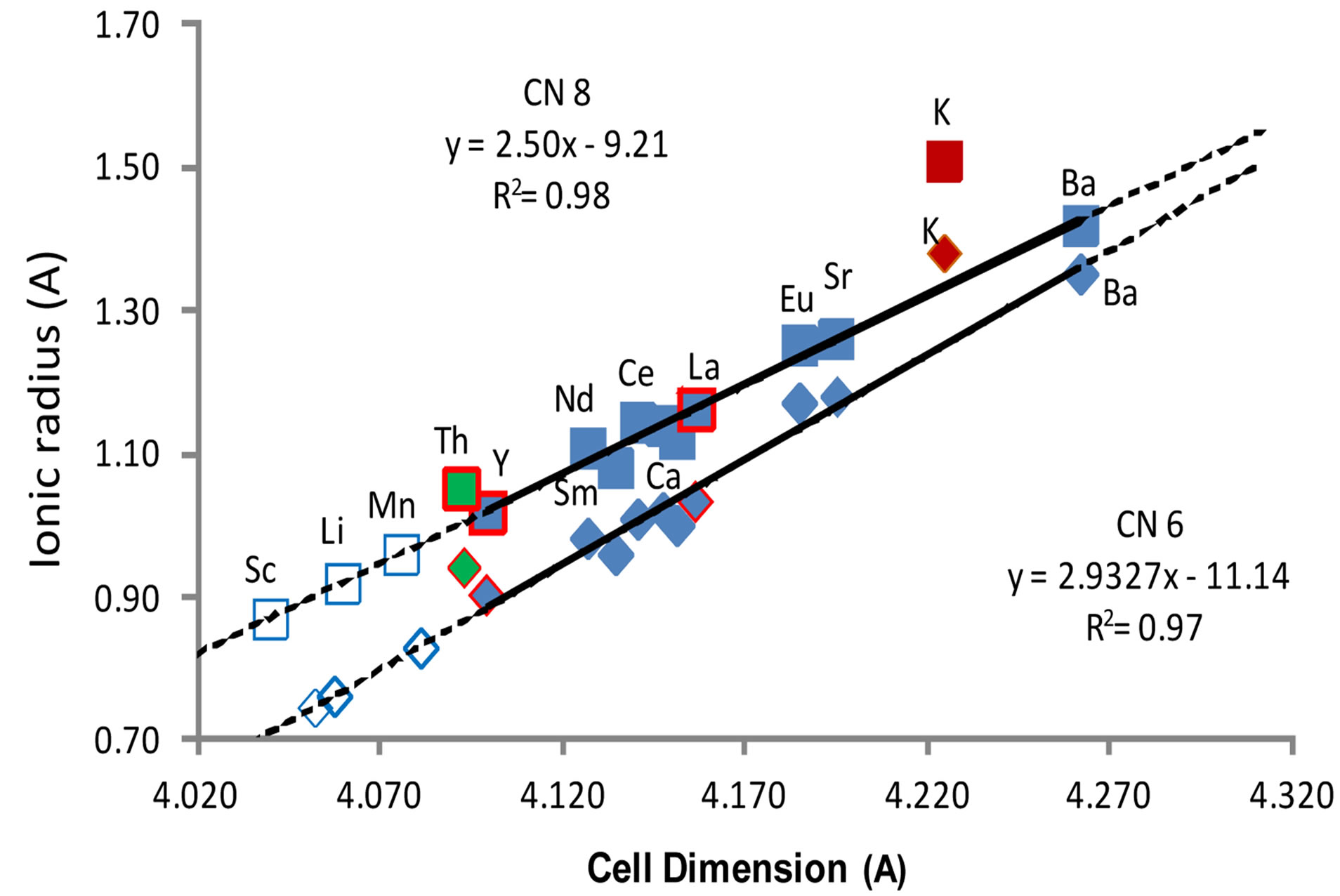
Figure 2. Cell parameter versus ionic radius for metal hexaborides listed in Table 1 (filled symbols). The square symbols represent ionic radii with eight-fold coordination (for the lowest valence state) and the diamond symbols are for six-fold coordination. Unfilled symbols are projected values of cell dimensions for possible hexaboride structures.
ve-fold coordinated ionic radii are plotted for the respecttive hexaborides, the eight-fold coordination K value lies closest to the twelve-fold trend line. Whilst circumstantial, this notional fit for KB6 cell parameter with ionic radius values suggests that potassium may favor a higher coordination in this structure type than normally attributed to the ion.
3.2. Bond Lengths
Bond lengths are reliably determined by least squares refinement of structure factors which take account of peak positions and peak intensities (moderated by absorption and other factors). The datasets that allow for calculation of bond lengths in metal hexaborides are limited and are listed in Table 1. Figure 3 provides detailed data on intra-octahedral (B-Bin) and inter-octahedral (BBout) bond lengths using MB6 structure determinations.
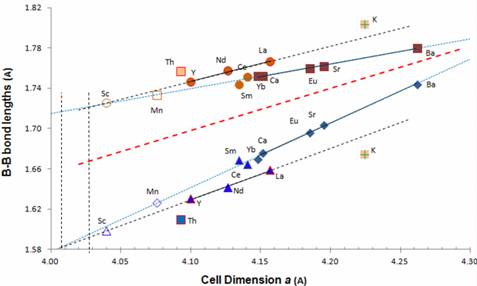
Figure 3. Plot of B-B (intra and inter) bond lengths for refined metal hexaboride structures. Filled symbols are data from Table 1; unfilled symbols are inferred values. The red dotted line represents equal B-B bond lengths in an MB6 structure.
Trend lines have been constructed for divalent metals (e.g. Ba, Sr, Eu, Ca, Yb) and for trivalent metals (e.g. La, Nd, Y) for both types of bonds. SmB6, CeB6, ThB6 and KB6 data, although plotted in Figure 3, have not been included in the trend line calculations as they represent unusual structure types (e.g. Kondo compounds or valence fluctuation) or different valence state(s) for the metal ion. Data for KB6 do not lie on either trend line and ThB6 is divergent from the trend.
In Figure 3, filled symbols represent data collected from sources listed in Table 1 with +3 metal valence symbols designated as circles and triangles for interand intra-octahedral bonds, respectively. Similarly, +2 metal valences are designated as square and diamond symbols for interand intra-octahedral bonds, respectively.
Unfilled symbols in Figure 3 represent inferred values for possible hexaboride structures as discussed below. The tendency for bond-lengths of Sm and Ce compounds to lie on, or close to, the divalent trend line in Figure 3 is noteworthy, given their predominantly trivalent charge in the MB6 structure [7], and may reflect the unusual character of these two dense Kondo structures.
Symbols for known superconductors in this suite of hexaborides are designated with a red border. Each superconducting compound has a significantly greater bond length difference between the interand intra-octahedral bonds than other MB6 structures of similar cell dimension. Thus, for a particular electron charge, the bonds between boron octahedra are shorter and the bonds within the octahedra are longer for superconducting than for non-superconducting MB6 structures. Note that while YB6 and LaB6 show superconducting properties, the LaB6 transition is at a very low temperature [3] and electronic properties are highly subject to small substitutions (e.g. <0.01 mole% Eu shifts from semiconducting to metallic [4]) and may, in effect, be considered a “weak superconductor”.
Table 1 lists the metal-boron bond length for structure refinements of metal hexaborides with estimated values for some structures indicated in italics. Where the ex plicit M-B value is not tabulated in an earlier literature reference, the formula: a (0.5 + z2)1/2 is used to calculate the metal-boron value [6] based on the other critical crystallographic parameter for refinement, z, the position of the B atom as noted above.
Comparison of B-B and M-B bond lengths shows that B-Bout and B-Bin vary by about 8% and 3.4% in value, respectively while the M-B bond varies by 4.3%. This latter range of values for M-B bonds is similar to the cell dimension change (~4% overall). These differences in bond lengths, particularly the larger relative change for B-Bout, suggest that the boron framework cooperatively adjusts both the B6 octahedra and, predominantly, the bonds between B6 octahedra. While there is some level of rigidity to the overall structure, this framework flexibility is an important contributor to phase stability for these hexaborides. Given the symmetry-defined formula that relates B-Bout and B-Bin (B-Bout = a – 21/2B-Bin), larger changes in B-Bout are required to accommodate changes in B-Bin.
3.3. Cell Dimension Variations and Limits
As shown in Figure 3, calculated bond lengths based on structure refinements, particularly B-B bonds, reveal more detail than the linear trends for ionic radius. For this structure type, there will be a limit at which incorporation of a particular metal ion will result in a change of symmetry or phase relation. The trend lines in Figure 3 for both types of boron bonds in divalent and trivalent structures converge at smaller cell dimension. The convergence of these trends define a geometric limit for a cubic hexaboride structure and thus, sets a limit on likely ions that may be included in new forms of stoichiometric metal hexaborides. The trends in Figure 3 imply that the lower limit of cell dimension will range between 4.01A and 4.03A (dotted vertical lines in Figure 3). With reference to Figure 2, this suggests that ionic radii 0.80 < rR < 0.85 is a lower limit for an eight-fold coordinated metal. This lower limit is also consistent with published theoretical values of lattice constants for hexaboride structures [33].
An upper limit for the cell dimension of hexaborides is more difficult to predict as there are no divalent metal ions with ionic radius larger than Ba2+. Nevertheless, a single crystal study [34] of BaB6 showed that the structure remained stable to 400 K with cell dimension expansion to approximately 4.284A. This work suggests that larger metal ions may be incorporated into a hexaboride structure albeit these would be univalent (e.g. K, Cs, Rb and Fr). To date, only KB6 has been synthesized [11].
Ogita et al. [30] suggest that the term, a-2rR, describes the “cage space” [30,31] or the amount of space in the boron framework within which the M ion may move. A plot of a-2rR against cell dimension for divalent and trivalent metal ions gives an expected linear trend that appears counter-intuitive because as cell dimension decreases, the available cage space increases (data not shown). The cage space calculation [30] assumes the boron framework is rigid and that the predominant motion/vibration within the MB6 structure is related to the metal ion. According to Chernyshov et al. [31], the atomic thermal displacements of the metal ion increase with reduced cell dimension. This trend appears to correlate with softening of the acoustic modes for phonon spectra in the rare earth hexaborides [31] and to relative peak energy of Raman spectra [30] at <200 cm−1. However, a geometrical analysis of the hexaboride structure suggests these displacements would reduce with smaller lattice parameter.
Inspection of the region around the M ion shows that as B-Bin and B-Bout adjust dimensions (in six symmetry-related directions equally), the volumetric re-arrangement is that of an irregular truncated cube. To simplify our estimate of the change(s) in volume as bonds adjust to accommodate specific metal ions, we have calculated the volume bound by the boron octahedral edges defined as the “truncated cube volume” (Vtc) which is the truncated cube bound by the surfaces formed by B-Bin and B-Bout bonds surrounding the metal ion.
Figure 4 shows values for this truncated cube volume
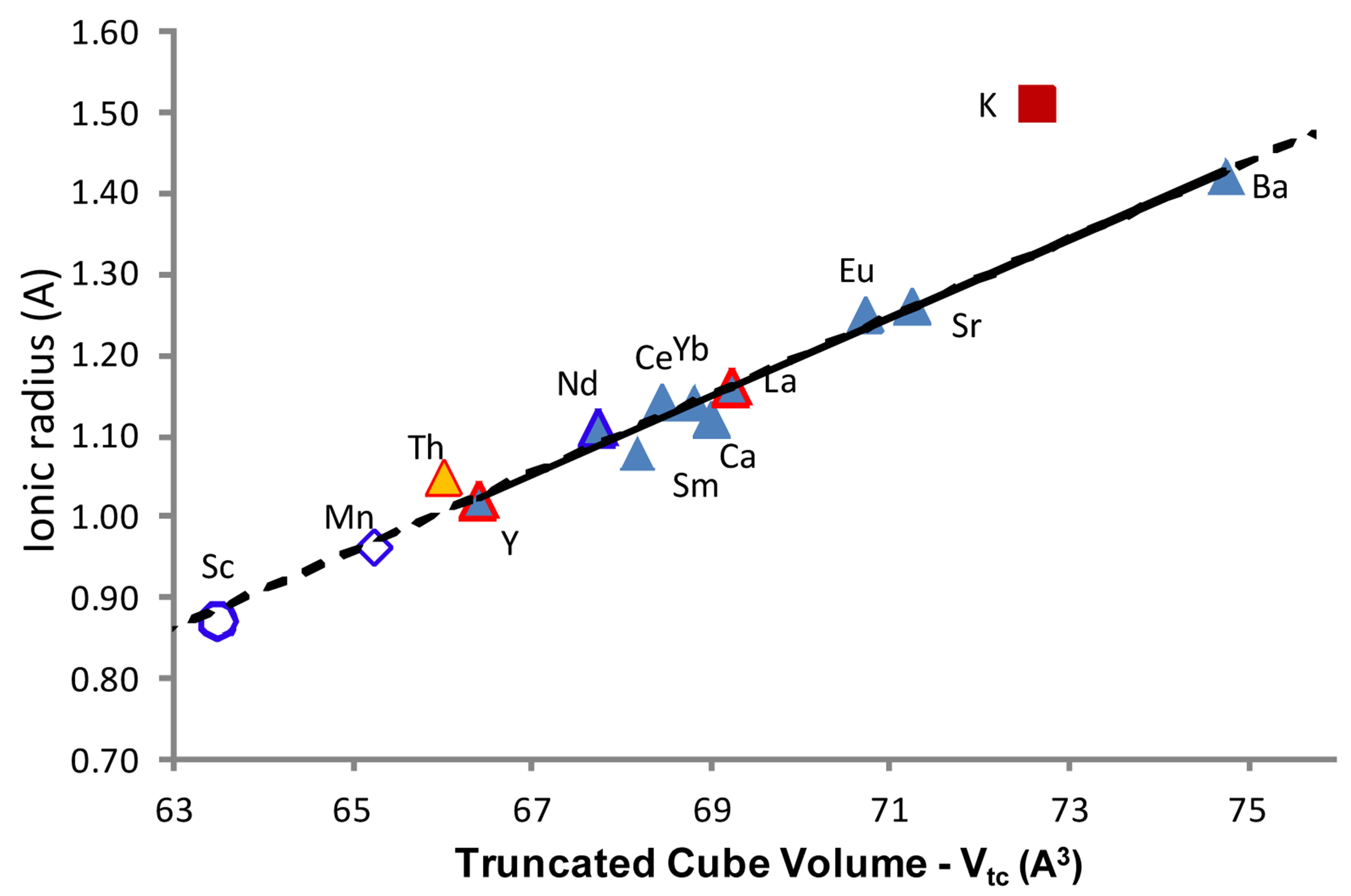
Figure 4. For structure refinements of MB6, the truncated cube volume surrounding the metal ion is positively related to the ionic radii.
(Vtc) plotted against the ionic radii for the relevant metal ion. Note that Vtc is not the volume contained within each boron B6 octahedra within, or at, the vertices of the unit cell (depending on the choice of origin)—but the volume surrounding the M ion in six symmetry-related axial directions.
There is a strong positive relationship between Vtc and metal ion radius for all refined structures. While the value for KB6 does not directly align with the trend line in Figure 4, the general relationship—a larger value of Vtc related to a larger ionic radius—applies. The trend in Figure 4 shows that within the MB6 structure, the overall space—bounded by boron atoms—surrounding the metal ion increases with ionic radius of the metal ion (and with cell dimension). This seems to indicate that as the cage contracts, the cage itself contributes more to its own stability, probably through repulsion between boron octahedra, but also with the octahedra acting as complex ligands bound to the central metal.
Figure 5 shows the variation of Vtc with B-B bond length difference, ΔBB, for the refined structures listed in Table 1. This plot shows that the highest values of ΔBB occur with KB6, YB6, NdB6, ThB6, LaB6 and CeB6—all metallic conductors—while other forms follow a decreasing trend of ΔBB with increased octahedral cage volume. The three known forms of superconducting hexaborides show higher values for ΔBB as shown in Figure 5 and, implicitly, in Figure 3. Hexaboride insulators are to the lower right side of Figure 5.
4. New Hexaborides
Trends in Figures 2-4 allow an estimate of cell dimension or Vtc for an unknown MB6 structure provided either the ionic radius or the cell dimension is known. For example, given a trivalent eight-fold coordinated ionic radius of 0.87 for Sc [32], the linear trend in Figure 2 provides an estimate of cell dimension for a putative
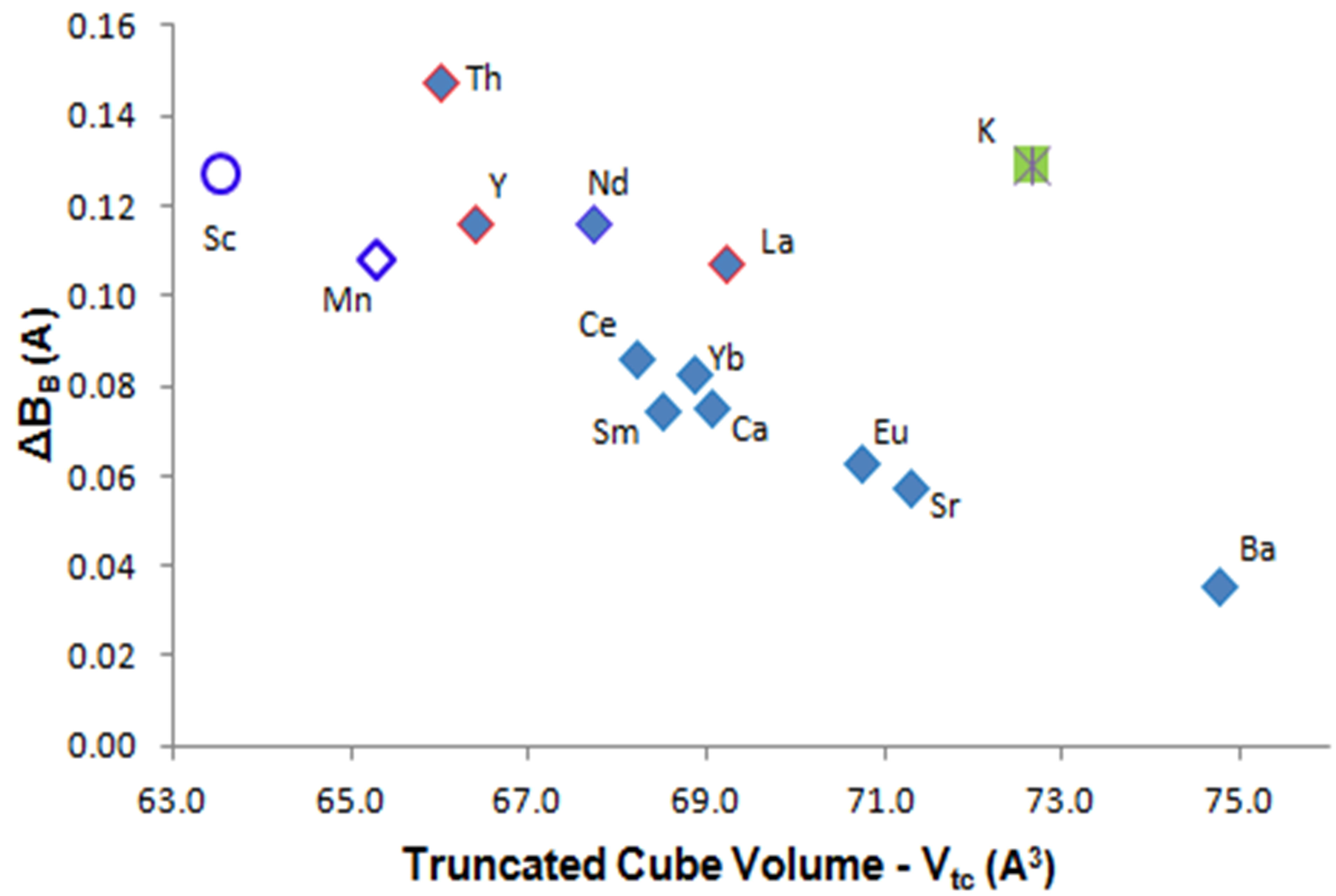
Figure 5. Bond length differences (i.e. B-Bin minus B-Bout) for structures refined in Table 1 plotted against truncated cube volume (Vtc). Unfilled symbols are inferred values for possible metal hexaborides.
ScB6 structure, a = 4.0398A. The elements Sc and Mn with +3 and +2 charge, respectively, are considered potential candidates for a metal hexaboride structure because they meet the minimum crystallographic requirements noted above. Accordingly, with determination of cell dimension from Figure 2, estimates of bond lengths, Vtc, and ΔBB have also been calculated and are shown in Figures 3-5. Following a similar argument, the eight-fold coordinated ionic radius for Li1+ is 0.92A [32] and infers that with a cell dimension of 4.06A, a LiB6 structure may be possible. A lower symmetry, but structurally-related compound, Li2B6, is well characterized [35].
Known hexaborides from Row IV of the Periodic Table are KB6 and CaB6 each of which have been synthesized with significantly different degrees of stoichiometry [12,34]. Other forms of hexaborides from this row are not documented. For potential structures with Sc and Mn, the estimated cell dimension, a, is greater than 4.03A, and the B–B bond lengths are substantially smaller than KB6 or CaB6; consistent with the influence of ionic radius on the overall structure. In each case, bond length estimates for these putative structures imply a stronger inter-octahedral bond and relatively smaller B6 octahedra compared with their Row IV counterparts. If it is possible to synthesize these MB6 compounds (M = Sc3+ or Mn2+), a comparison of experimental data with these simple estimates of structural parameters would be informative.
Barantseva and Yu [36] also examined the state of hexaboride syntheses at the time and concluded that it is impossible to make ScB6 except perhaps via high pressure. In their analysis [36], they argue that the difficulty of synthesis is due to the strong affinity of Sc atoms for B atoms rather than dimensional features related to ionic radii, structure and symmetry. Barantseva and Yu [36] propose a slightly larger cell dimension for ScB6 (a = 4.08A) than estimated from Figure 2, but develop an argument based on ionic polarisability and the relative influence on the M-B bond on overlapping boron orbitals particularly along the B-Bout dimension. We shall return to the viability of a ScB6 structure via theoretical band structure calculations below.
For Ti, only the +4 valence state allows an eight-fold coordination for which the ionic radius is estimated at 0.74A [32]. An estimated cell dimension of a possible TiB6 structure using the equation from the trend line in Figure 2 (but for a divalent or trivalent valence state) is 3.988A. This estimated cell dimension is significantly less than the estimated lower value for metal hexaborides and thus, suggests that stoichiometric TiB6 may be difficult to synthesize. As noted below, geometry optimizations in band structure calculations converge close to this value at a = 3.9802A even when the input value is nominally 4.08A.
5. Electronic Structures
Theoretical calculations of elastic, electronic and lattice dynamic parameters for metal hexaboride structures are ultimately constrained by geometry or crystal structure [33,34,37]. Valence state also influences these properties as divalent hexaborides are commonly insulators or semiconductors and trivalent hexaborides are commonly metallic [5,33,37]. As noted earlier, KB6 is identified as not a “normal” metal [12] and ThB6 is a paramagnetic metal [13]. Defects clearly influence electronic properties in this structure type and are considered below.
5.1. Stoichiometry
Shirai and Uemura [38] show that for icosahedral boron structures valence counting has a valid place in the interpretation of covalently bonded structures including borides and boron carbides. This simple analysis is particularly useful for high symmetry structures which tend to incorporate vacancies and interstitials into large unit cells and for structures with close similarity in elemental configurations (such as with boron and carbon) for which experimental quantification may be difficult [39]. In addition, when the electronic structure determined by experiment seems to be in disagreement with a band structure calculation, Shirai and Uemura [38] suggest that this is an indicator for the presence of defects.
As shown in Table 1 and other structural studies [27], the level of defects—identified by refinement techniques as stoichiometry—for these hexaboride structures is low except for KB6 (K~0.94) and ThB6 (B~6.15). For all other structures identified in this work, the nonstoichiometry for a particular hexaboride structure is less than 2%. Experimental and theoretical values of lattice constants and bulk moduli for defect-free structures compare well for Ca, Sr, Ba, Eu, Yb, Y, La and Cd hexaborides [34]. Experimental data from NMR analysis [37] of YB6 is also strongly supported by theoretical calculations of band structure, density of states and valenceelectron distributions. Estimates for z, the boron 6f position shows good correlation [34,40] for YB6, BaB6 and ThB6.
Compositions further from stoichiometry are observed in KB6 (e.g. K<0.84B6 [12]) and ThB6 (e.g. Th0.78B6 [41]) and occur in other hexaborides [42] (e.g. Sm0.96B6). Indeed, (K1−x)B6 shows a significant change of color with greater non-stoichiometry (from “Bordeaux red” to black) that is dependent on synthesis temperature [12]. This work [11,12] shows that the valence bands of KB6 are partially empty while Katsura et al. [43] show a clear difference in calculated electronic properties between stoichiometric and hole-doped KB6.
Very small concentrations of defects influence electronic properties in structures with small, or no apparent, band gap [37]. For example, in CaB6 the presence of boron-related defects (the difference between 6N and 3N purity or << 1%) are closely associated with carrier doping and the formation of mid-gap states 0.18 eV below the conduction band [5]. Small amounts of La substitution for Ca are also associated with magnetic effects [44]. Vacancy defects also influence the complexity of Raman spectra—particularly the A1g and Eg bands—and reduce the basic cubic symmetry of hexaborides [9]. Yahia et al. [45] also show that an excess of boron in the hexaboride structure influences local symmetry.
5.2. Valence Electrons
In contrast to boride structures [38], valence counting for metal hexaborides requires consideration of the B6 octahedra which demonstrate strong covalence [28,46] while partially ionic character is evident for the M-B bond. Recent work [28,29] on electron distribution in SmB6 and CeB6 shows there is a high sensitivity of electron distribution to a) temperature and b) anharmonic vibrations. In CeB6, donated electrons localize around the B-Bout bonds with reduction in temperature supporting the notion that the boron framework is not “rigid” but flexible.
Simple valence counts for metal ions imply that for charge balance to the overall structure, the charge on a boron atom, or the B6 moiety, will accommodate a wide range of values (from −1 to −4) depending on the metal ion. This variability of charge balance or of bond populations in the boron framework is explicitly revealed [25] in theoretical calculations of the electronic structure of LaB6. These calculations show that the B-Bout bond is almost completely covalent while other bonds within the B6 octahedra display mixed covalent and ionic character [25].
This capacity for boron atoms to show valence ambiguity within a responsive framework of connected octahedra (i.e. within a specific structure type) engenders a high sensitivity to subtle variations in electron distribution and, as a consequence, physical properties are also highly influenced by the presence of boron-related vacancies or defects. This sensitivity is manifest in electronic and magnetic properties across a structure type which displays the gamut of physical properties.
Schmitt et al. [34] calculate the band structure for BaB6 and CaB6 using DFT and show that the total energy, Etot, depends on the positional parameter, z, for the minimum energy range. In addition, the direct band gap for both structures [34] depends linearly on z while SmB6 shows similar dependence [42]. Calculations show that lowering z below the equilibrium value results in significant overlap of valence and conduction bands [34]. In the case of BaB6 and CaB6 these shifts in z value, which may be less than 0.003 au, are consistent with a change from metallic to insulating properties [34].
Figure 6 shows the calculated values for z derived from refinements of experimental data shown in Table 1. These z values are plotted against B-Bin and B-Bout values from each structure refinement. Each metal ion of the hexaboride structure is identified in Figure 6. B-Bout bond length values encompass a wider range of values compared with B-Bin values across these structures. The z values, except for KB6, show a strong linear trend with B-Bout values (r = 0.96) and show a difference in value of 0.008 au (~0.03 nm). Metallic and superconducting hexaborides have refined values for z < 0.201 and, as noted above, this implies that the difference in bond lengths, ΔBB, is a key indicator of physical or electronic properties. Note also that B-Bout values for the superconducting hexaborides are <0.200 and furthest from the position at which both bond lengths are equivalent [34] (designated by the red dotted line at z = 0.207 in Figure 6).
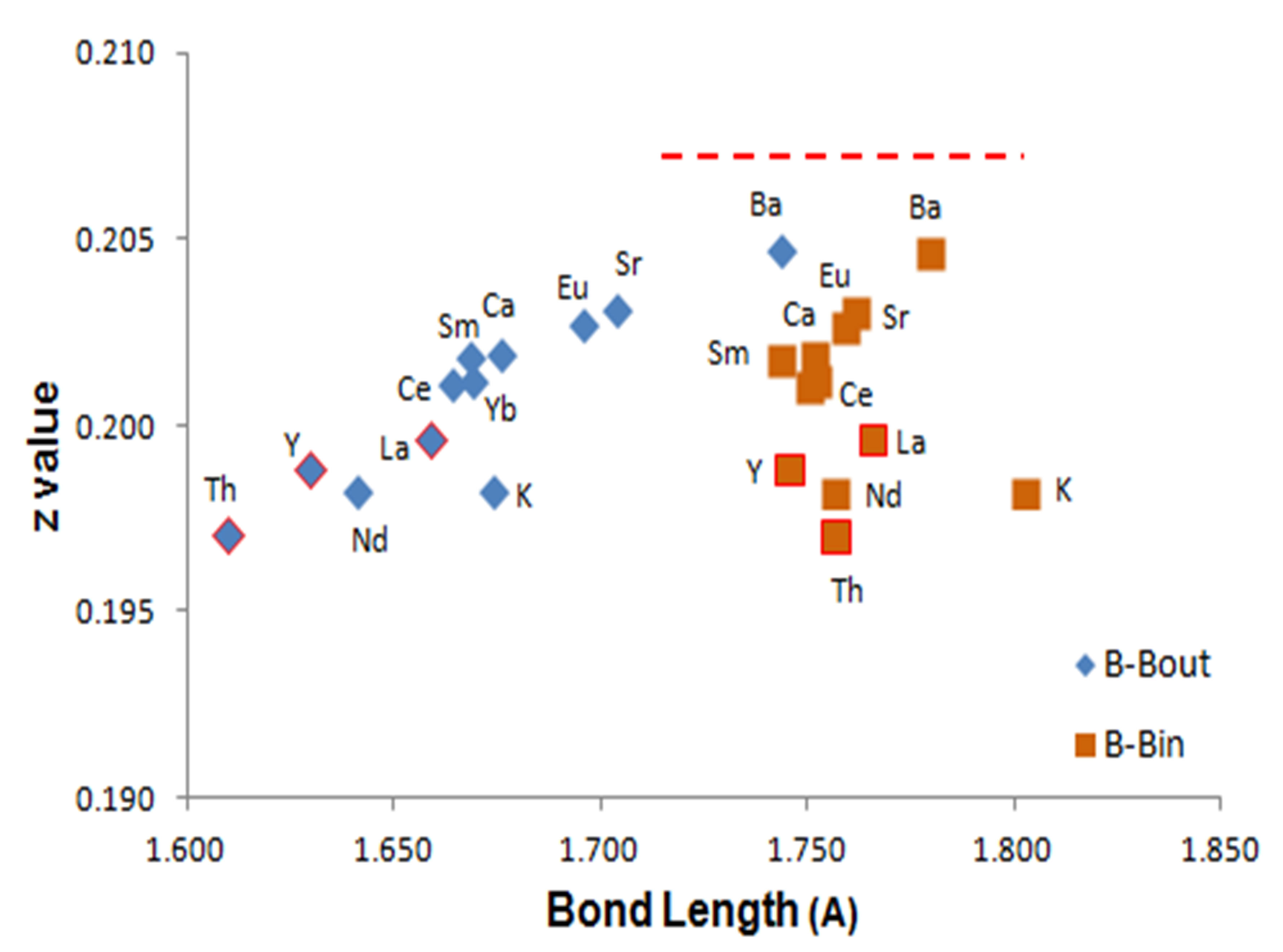
Figure 6. Variation of MB6 6f atomic position with average B-B bond lengths for B-Bin and B-Bout. The red dotted line signifies the z values at which both bonds are of equal length.
KB6 is also a metal hexaboride with unusual properties which may reflect not only non-stoichiometry (and the presence of defects) but also the presence of localized electrons [11]. We suggest that cell parameter data are important indicators of unusual electronic properties and is evident from the refined powder diffraction data [11] for K0.97B6. For example, cell parameters reduce systematically with lower temperature but show dramatic changes below 100 K [12]. At 60 K, the B6 octahedra contract to a minimum size and then, with further reduction in temperature, increase rapidly to a local maximum at about 40 K. This bulk behavior appears related to a magnetic hysteresis effect below 100 K identified by measurements of magnetic susceptibility and Seebeck coefficient [11,12]. This behavior also supports the notion that the boron framework is, within limits, flexible and responsive to the electronic structure of the hexaboride.
5.3. Band Structure Calculations
For LaB6 and YB6, structural parameters determined from single crystal studies (Table 1) are used. Lattice parameters for ScB6 suggested by Barantseva and Yu [36] and based on linear extrapolation of the data in Figure 2 are utilized in calculations. Given a theoretical ScB6 structure, a range of values for the key boron position at (1/2, 1/2, z) has been included in these calculations. We have also attempted to calculate the band structures for hypothetical TiB6 and MnB6 using the estimated cell dimensions inferred from the compiled crystallographic trends given above in Figures 2 and 3. The reciprocal space structure for these calculations is shown in Figure 7 as a reference to lattice points and crystallographic directions.
The calculated band structure for LaB6 in this study is similar to that reported by Hossain et al. [25] who provide a detailed interpretation of the electronic structure. The band structure for YB6 is similar to that described by Xu et al. [37] and is shown in Figure 8(a).
For ScB6, Figure 8(b) shows the LDA band structure calculation and density of states for a hypothetical ScB6 with a = 4.05A and z = 0.2 using the origin as described in Figure 7. A second calculation with a = 4.08A and z = 0.2 shows similar structure largely because geometry optimization takes the final lattice parameters to similar values. The primary differences in band structure are those near the Fermi energy.
Slight changes in the cross-over of valence electrons on the X-R join near the Fermi surface are observed when comparing band structure calculations between LaB6, YB6 and ScB6, and sometimes within the same compounds, when modeled under different approximations. This change in energy levels for valence electrons with minimal change to cell dimension (~0.05A) is consistent with a boron framework that is highly responsive
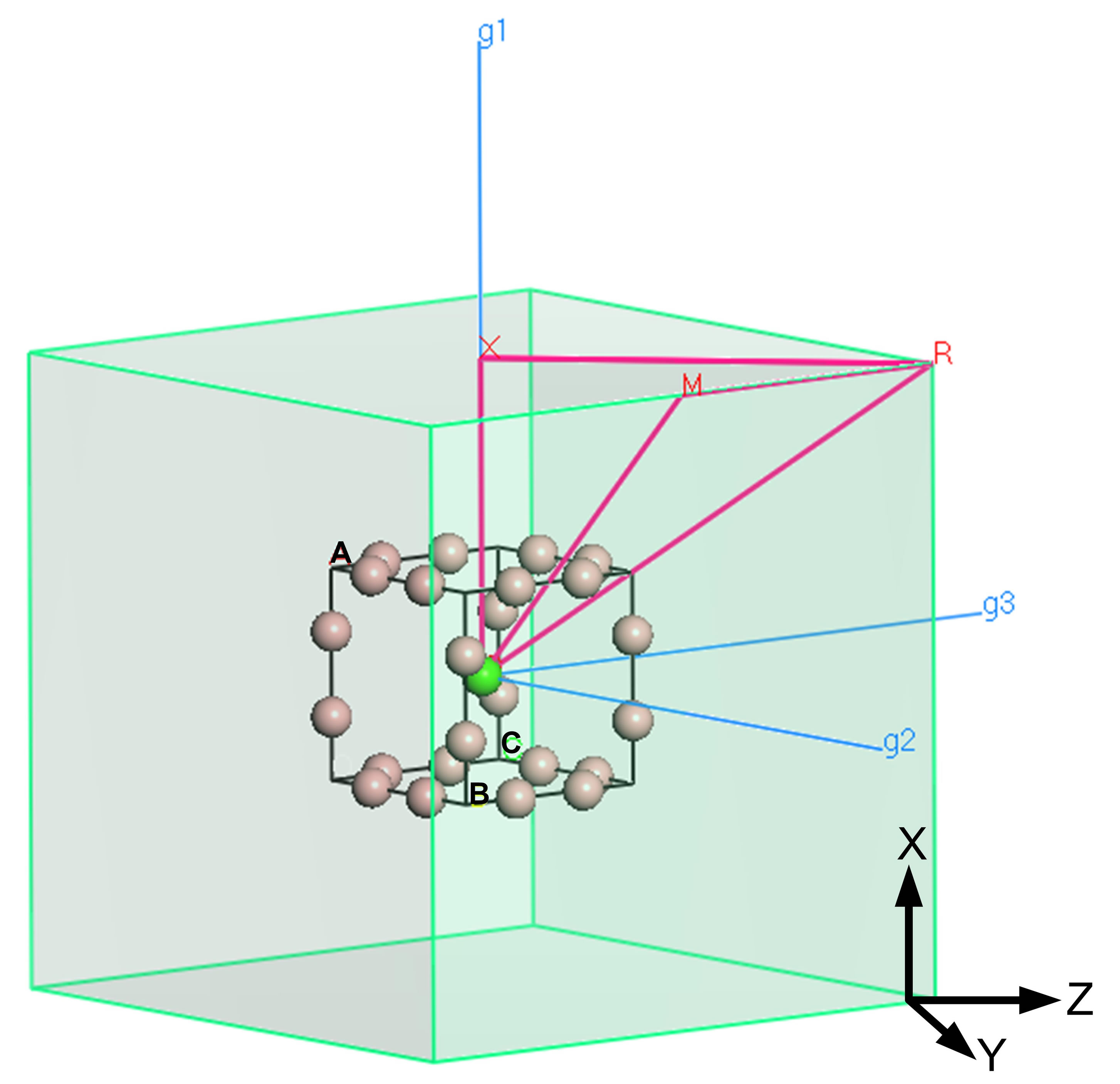
Figure 7. Reciprocal space configuration and crystallographic annotation for electronic structure calculations.
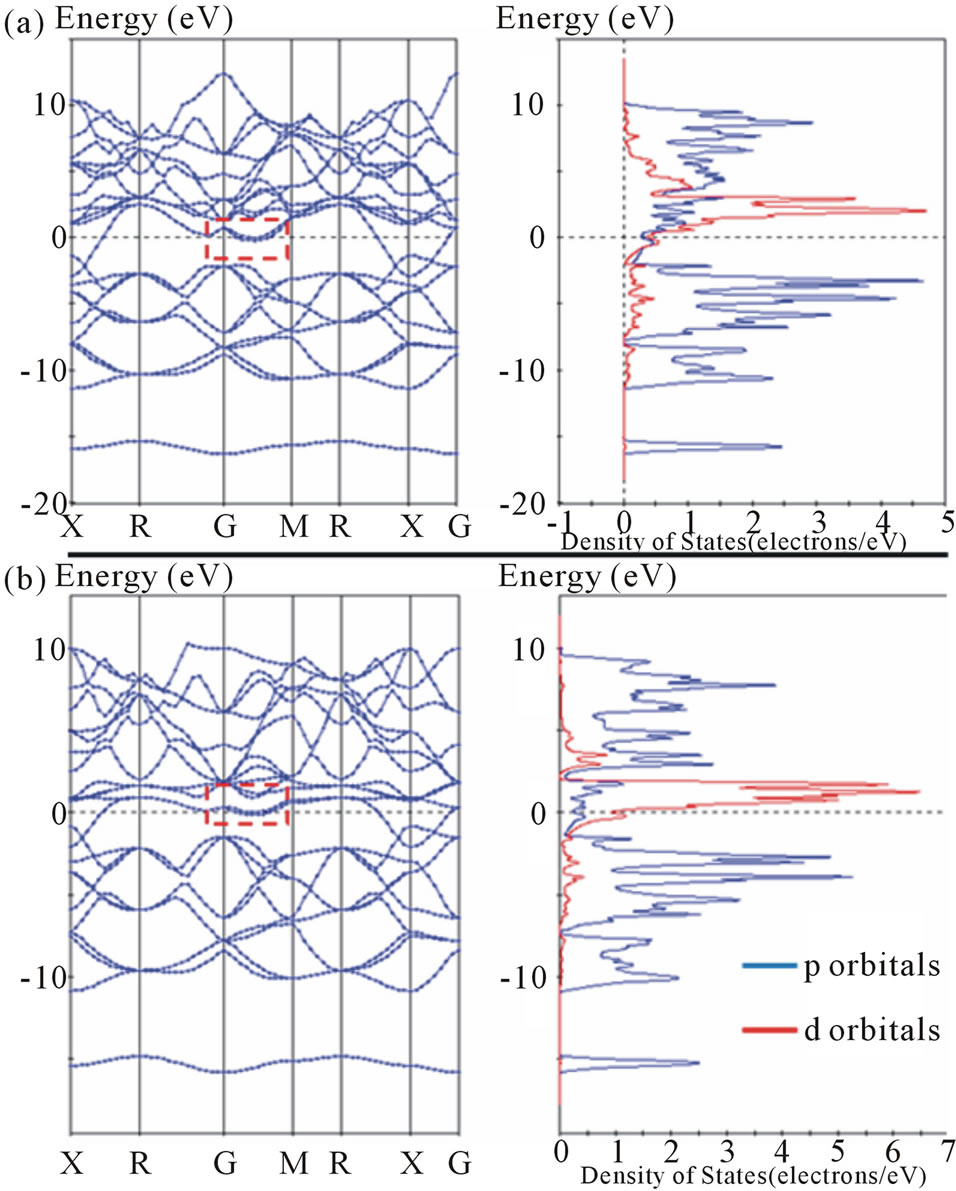
Figure 8. LDA band structure calculation and DOS for (a) YB6 structure and (b) ScB6 structure.
to subtle structural variations.
A second feature of note is the almost flat region along the G-M join to the Fermi energy (dotted outline in Figure 8). As pointed out by Hossain et al. [25], this region is the most important for electronic properties. The region encloses a small pocket of electrons just under the Fermi energy. The G-X join describes the orientation from the centre of the cubic lattice to the centre of the cube face in reciprocal space and provides a direct interconnected path from deeper regions in the valence band to the G-M join. In this region, the join presents small cusps at G that may represent hole pockets.
The height from the cusp to the Fermi energy decreases in order from LaB6, YB6 and ScB6. These pockets, in close proximity to each other and to the Fermi energy, resemble conditions suited to formation of Bogoliubov quasiparticles (i.e. broken Cooper pairs). These quasiparticles are an important feature of the BCS model and high Tc superconductivity models [47]. Thus, the flatter band structure of the conduction orbitals in ScB6 suggests that it may be possible to realize superconductivity in this hexaboride if synthesis is successful.
Calculations that include atoms with increased valence electrons in the 3d transition metal series result in a significantly increased DOS with increased d-character at the Fermi energy. This can be seen for band structure calculations of ScB6 and MnB6 shown in Figures 8(b) and 9. In both cases, the relatively narrow character of the 3d bands is also apparent. ScB6 displays d character at the Fermi energy interconnected in a few reciprocal space directions to higher energy conduction bands. However, MnB6 displays a gap of about 2.5 - 3.0 eV between orbitals at the Fermi energy and the next group of orbitals in higher energy conduction bands. In addition, the nearly tangential nature of bands to the Fermi surface for MnB6 is more extensive over a wider range of reciprocal space directions. The possibility that this additional 3d electron doping with high DOS at the Fermi energy favors band structure modulations that assist superconductivity is worthy of experimental verification.
In order to better understand the influence of metal ions on band structure and DOS for the MB6 structure type, we have undertaken LDA calculations for four different structures with increasing nominal metal ion charge. These structures are (a) a “metal-free” boron framework of B6 octahedra, (b) KB6, (c) CaB6 and (d) LaB6 using the parameters given in Table 1. These band structures are shown in Figure 10. The detail of conduction bands and DOS for KB6, CaB6 and LaB6 are as described previously. The notable feature of this comparison is that the overall shape of the valence and conduction bands is largely the same irrespective of the metal as shown in Figure 10 and previously identified by Perkins [21] for LaB6 and CaB6. The relative position of the valence and conduction bands with respect to the Fermi energy depends on the type of metal ion and reflects the atomic configuration of the metal.
With respect to the boron framework, introduction of a metal primarily lowers the overall energy of the conduction orbitals, while simultaneously adjusting their relative value compared to the Fermi energy. This comparison in Figure 10 shows that the shape and density of the orbitals are primarily defined by the boron framework of B6 octahedra alone. The energy reduction to the overall
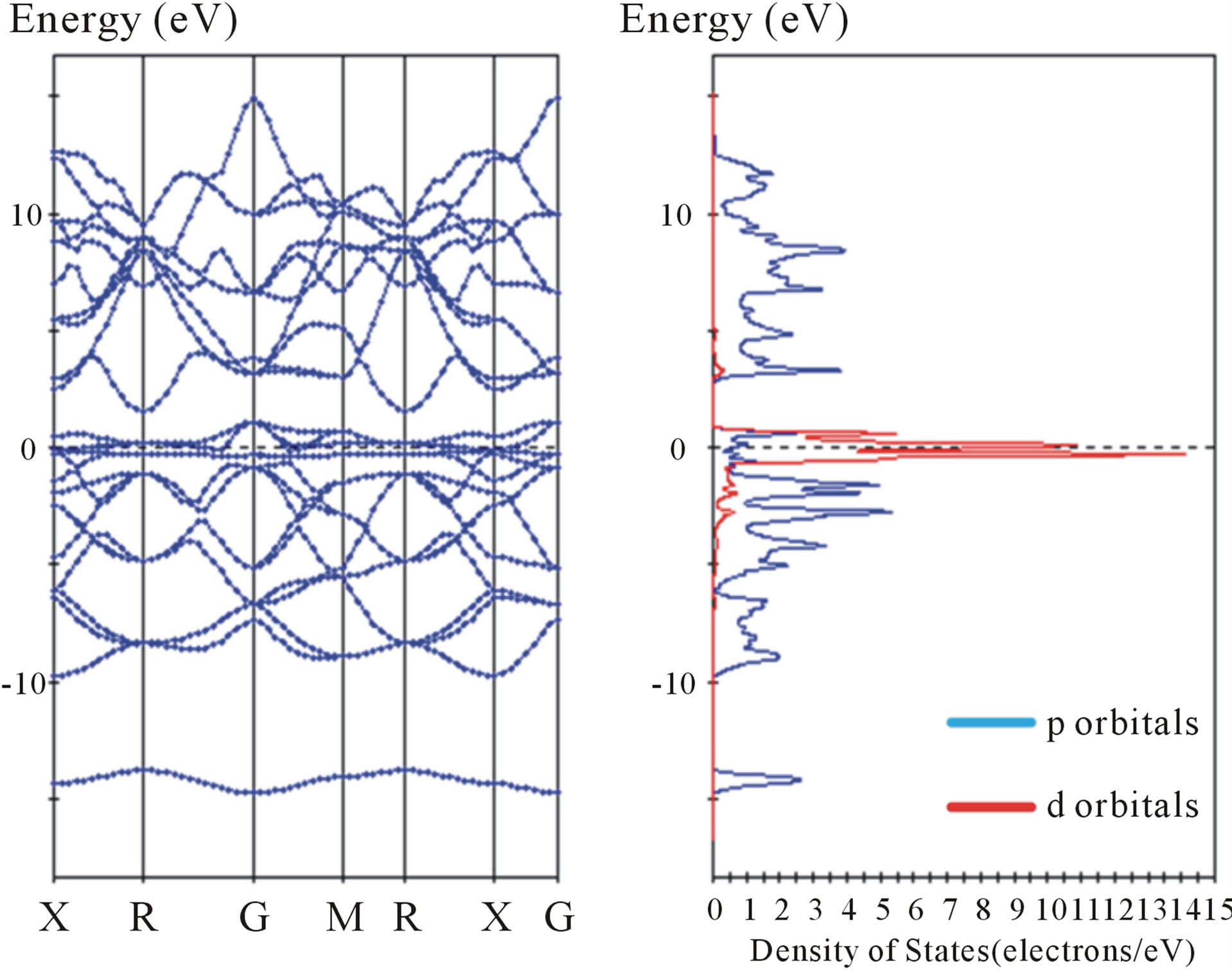
Figure 9. LDA band structure calculation and DOS for MnB6 structure.
framework by introduction of a metal ion largely represents a voltage polarization of the conduction band and ranges from 1 eV to 6 eV (see Figure 10). When the metal has d character, such as Sc, Y and La with 3d, 4d and 5d orbitals, respectively, the metal also introduces d character into the Fermi surface to an extent comparable to the 2p character contributed by the boron framework as shown in Figure 10.
Band structure calculations were also performed for TiB6 to evaluate the nature of the Fermi surface in this putative structure. Band structure calculations for TiB6 follow the overall trend for DOS and narrow band structure identified for 3d transition metals such as ScB6 and MnB6 discussed above. In general, geometry optimization for 3d transition metal elements within the hexaboride structure converge at significantly reduced lattice parameters with incrementally lower values as the number of d valence electrons increases. Under the same initial parameters, convergence for TiB6, after allowing for unit cell optimization, occurs at cell dimension values just under 4.0A, consistent with projections from data shown in Figure 2. Thus, we suggest that MnB6 and TiB6 are structurally unstable forms at stoichiometric, or near stoichiometric, compositions. These compositional forms are more likely to stabilize with, for example, carbon substitution within the boron framework. This possibility is analogous to the existence of symmetrically equivalent, isotypic and isoelectronic compounds NaB5C and KB5C [48].
6. Conclusion
Linear extrapolations of high quality crystallographic data suggest that other types of metal hexaborides, such as ScB6 and MnB6, may be structurally feasible. While we have not determined the thermodynamic stability of
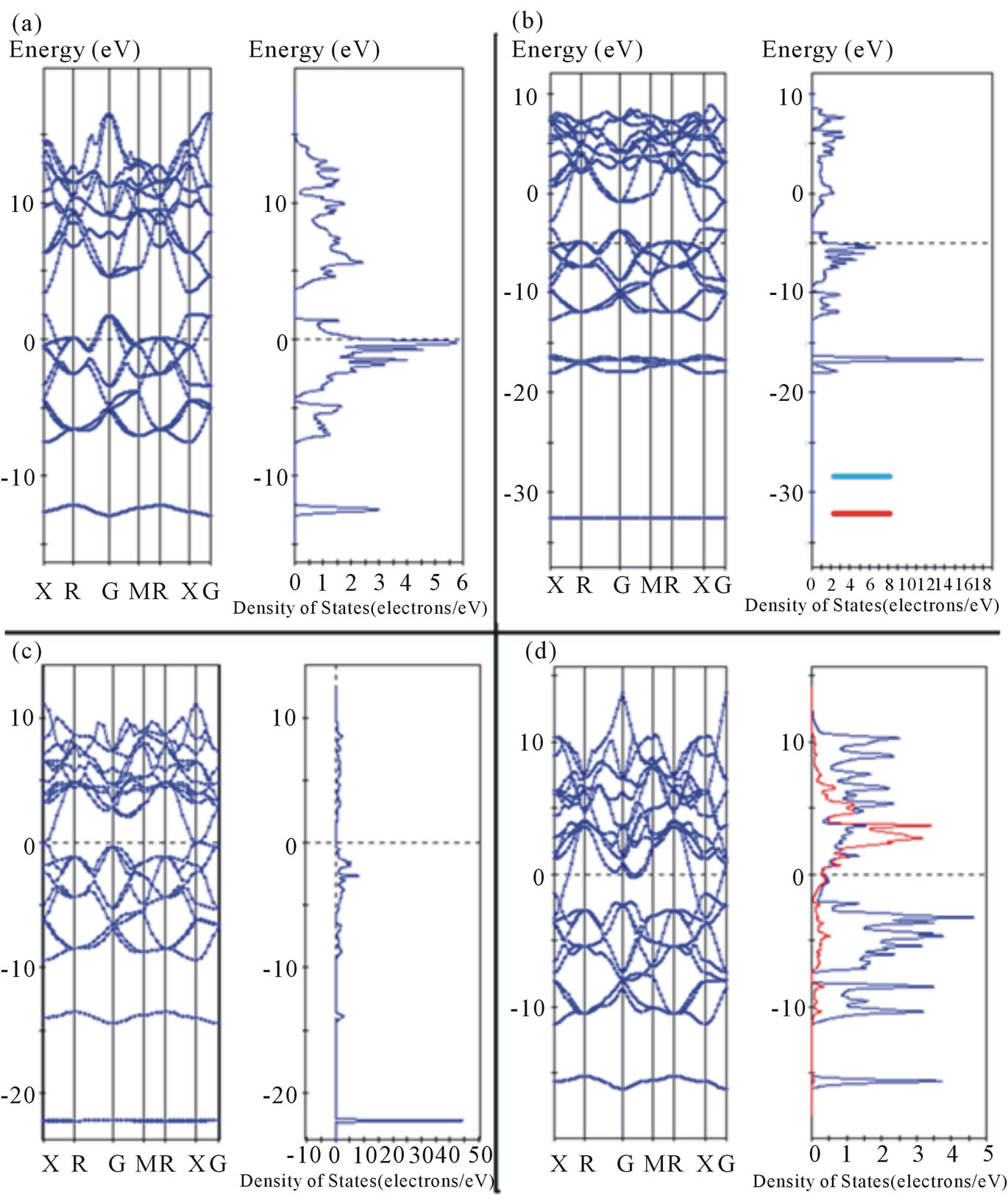
Figure 10. Band structure calculations and DOS for (a) B6 framework without a metal ion, (b) KB6, (c) CaB6 and (d) LaB6. Note the overall similarity of the conduction band in all four structures and lowering of energy with introduction of a metal ion.
these hexaborides, the possibility of their existence awaits facile synthesis methods that exploit kinetic drivers rather than thermodynamic. Electronic structure calculations for these possible new forms of hexaboride suggest that TiB6 is unlikely to form and that MnB6 may also be unstable. On the other hand, a well-defined band structure for ScB6, and similarity to both YB6 and LaB6 suggest that this hexaboride may show metallic or superconducting properties if synthesized.
7. Acknowledgements
We wish to acknowledge QUT for support of this research.
REFERENCES
- T. H. Geballe, K. Andres, E. Corenzwit, G. W. Hull and J. P. Maita, “Superconductivity and Antiferromagnetism in Boron-Rich Lattices,” Science, Vol. 159, No. 3814, 1968, pp. 530-531. http://dx.doi.org/10.1126/science.159.3814.530
- S. Souma, H. Komoda, Y. Iida, T. Sato, T. Takahashi and S. Kunii, “Direct Observation of Superconducting Gap in YB6 by Ultrahigh-Resolution Photoelectron Spectroscopy,” Journal of Electron Spectroscopy and Related Phenomena, Vol. 144-147, 2005, pp. 503-506. http://dx.doi.org/10.1016/j.elspec.2005.01.125
- R. J. Sobczak and M. J. Sienko, “Superconductivity in the Hexaborides,” Journal of the Less Common Metals, Vol. 67, No. 1, 1979, pp. 167-171. http://dx.doi.org/10.1016/0022-5088(79)90088-2
- J.-P. Mercurio, J. Etourneau, R. Naslain, P. Hagenmuller and J. B. Goodenough, “Proprietes Electriques et Magnetiques des Solutions Solides LaxEu1-xB6,” Journal of Solid State Chemistry, Vol. 9, No. 1, 1974, pp. 37-47. http://dx.doi.org/10.1016/0022-4596(74)90052-8
- B. K. Cho, J.-S. Rhyee, B. H. Oh, M. H. Jung, H. C. Kim, Y. K. Yoon, J. H. Kim and T. Ekino, “Formation of Midgap States and Ferromagnetism in Semiconducting CaB6,” Physical Review B, Vol. 69, No. 11, 2004, Article ID: 113202. http://dx.doi.org/10.1103/PhysRevB.69.113202
- C.-H. Chen, T. Aizawa, N. Iyi, A. Sato and S. Otani, “Structural Refinement and Thermal Expansion of Hexaborides,” Journal of Alloys and Compounds, Vol. 366, No. 1-2, 2004, pp. L6-L8. http://dx.doi.org/10.1016/S0925-8388(03)00735-7
- J. M. Tarascon, Y. Isikawa, B. Chevalier, J. Etourneau and P. Hagenmuller, “Valence Transition of Samarium in Hexaboride Solid Solutions Sm1-xMxB6 (M=Yb2+, Sr2+, La3+, Y3+, Th4+),” Journal of Physique, Vol. 41, No. 10, 1980, pp. 1125-1140.
- M. K. Blomberg, M. J. Merisalo, M. M. Korsukova and V. N. Gurin, “Single-Crystal X-Ray Diffraction Study of NdB6, EuB6 and YbB6,” Journal of Alloys and Compounds, Vol. 217, No. 1, 1995, pp. 123-127. http://dx.doi.org/10.1016/0925-8388(94)01313-7
- Z. Yahia, S. Turrell, G. Turrell and J. P. Mercurio, “Infra-red and Raman Spectra of Hexaborides: Force-Field Calculations and Isotopic Effects,” Journal of Molecular Structure, Vol. 224, 1990, pp. 303-312. http://dx.doi.org/10.1016/0022-2860(90)87025-S
- S. Otani, H. Nakagawa, Y. Nishi and N. Kieda, “Floating Zone Growth and High Temperature Hardness of RareEarth Hexaboride Crystals: LaB6, CeB6, PrB6, NdB6, and SmB6,” Journal of Solid State Chemistry, Vol. 154, No. 1, 2000, pp. 238-241. http://dx.doi.org/10.1006/jssc.2000.8842
- J. Etourneau, A. Ammar, A. Villesuzanne, G. Villeneuve, B. Chevalier and M.-H. Whangbo, “Unusual Hysteresis in the Magnetic Susceptibility of Cubic Hexaboride KB6,” Inorganic Chemistry, Vol. 42, No. 14, 2003, pp. 4242- 4244. http://dx.doi.org/10.1021/ic034018x
- A. Ammar, M. Menetrier, A. Villesuzanne, S. Matar, B. Chevalier and J. Etourneau, “Investigation of the Electronic and Structural Properties of Potassium Hexaboride, KB6, by Transport, Magnetic Susceptibility, EPR and NMR Measurements, Temperature-Dependent Crystal Structure Determination, and Electronic Band Structure Calculations,” Inorganic Chemistry, Vol. 43, No. 16, 2004, pp. 4974-4987. http://dx.doi.org/10.1021/ic049444c
- T. Konrad, W. Jeitschko, M. E. Danebrock and C. B. H. Evers, “Preparation, Properties and Crystal Structures of the Thorium Chromium Borides ThCrB4 and ThCr2B6; Structure Refinements of CeCr2B6, ThB4 and ThB6,” Journal of Alloys and Compounds, Vol. 234, No. 1, 1996, pp. 56-61. http://dx.doi.org/10.1016/0925-8388(95)01993-6
- S. F. Matar and J. Etourneau, “The Electronic Structures of Uranium Borides from Local Spin Density Functional Calculations,” International Journal of Inorganic Materials, Vol. 2, No. 1, 2000, pp. 43-51. http://dx.doi.org/10.1016/S1466-6049(00)00006-4
- L.-H. Bao, J.-X. Zhang, S.-L. Zhou and Tegus, “Synthesis, Thermionic Emission and Magnetic Properties of (NdxGd1-x)B6,” Chinese Physics B, Vol. 20, No. 5, 2011, Article ID: 058101.
- J.-M. Mignot, G. Andre, M. Sera and F. Iga, “Magnetic Phase Diagram of CexNd1-xB6 Solid Solutions,” Journal of Magnetism and Magnetic Materials, Vol. 310, No. 2, 2007, pp. 738-740. http://dx.doi.org/10.1016/j.jmmm.2006.10.523
- M. K. Blomberg, M. J. Mersialo, M. M. Korsukova and V. N. Gurin, “Single-Crystal X-Ray Diffraction Study on Ce1-xLaxB6 Solid Solutions,” Journal of the Less Common Metals, Vol. 168, No. 2, 1991, pp. 313-319. http://dx.doi.org/10.1016/0022-5088(91)90313-S
- L. Vegard, “Die Konstitution der Mischkristalle und die Raumfüllung der Atome,” Zeitschrift für Physik, Vol. 5, No. 1, 1921, pp. 17-26. http://dx.doi.org/10.1007/BF01349680
- G. A. Wigger, C. Beeli, E. Felder, H. R. Ott, A. D. Bianchi and Z. Fisk, “Percolation and the Colossal Magnetoresistance of Eu-Based Hexaboride,” Physical Review Letters, Vol. 93, No. 14, 2004, Article ID: 147203. http://dx.doi.org/10.1103/PhysRevLett.93.147203
- V. I. Matkovich, Ed., “Boron and Refractory Borides,” Springer-Verlag, Berlin, 1977, 656 p. http://dx.doi.org/10.1007/978-3-642-66620-9
- P. G. Perkins, “The Electronic Structures of the Hexaborides and the Diborides,” In: V. I. Matkovich, Ed., Boron and Refractory Borides, Springer-Verlag, Berlin, 1977, pp. 31-51. http://dx.doi.org/10.1007/978-3-642-66620-9_4
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, “First Principles Methods Using CASTEP,” Zeitschrift fur Kristall, Vol. 220, No. 5-6, 2005, pp. 567-570.
- D. S. Sholl and J. A. Steckel, “Density Functional Theory —A Practical Introduction,” Wiley, Hoboken, 2009. http://dx.doi.org/10.1002/9780470447710
- V. Milman, B. Winkler, J. A. White, C. J. Pickard, M. C. Payne, E. V. Akhmatskaya and R. H. Nobes, “Electronic Structure, Properties, and Phase Stability of Inorganic Crystals: A Pseudopotential Plane-Wave Study,” International Journal of Quantum Chemistry, Vol. 77, No. 5, 2000, pp. 895-910. http://dx.doi.org/10.1002/(SICI)1097-461X(2000)77:5<895::AID-QUA10>3.0.CO;2-C
- F. M. Hossain, D. P. Riley and G. E. Murch, “Ab Initio Calculations of the Electronic Structure and Bonding Characteristics of LaB6,” Physical Review B, Vol. 72, No. 23, 2005, Article ID: 235101. http://dx.doi.org/10.1103/PhysRevB.72.235101
- G. Ning and R. L. Flemming, “Rietveld Refinement of LaB6: Data from µXRD,” Journal of Applied Crystallography, Vol. 38, 2005, pp. 757-759. http://dx.doi.org/10.1107/S0021889805023344
- A. Malyshev, D. Chernyshov, V. Trounov, V. Gurin and M. Korsukova, “Crystal Structure of Nd11B6 in the Temperature Range 23-300K: A High-Resolution Powder Neutron Diffraction Study,” Proceedings of the 11th International Symposium on Boron, Borides and Related Compounds, JJAP Series 10, 1994, pp. 19-20.
- K. Tanaka and Y. Onuki, “Observation of 4f Electron Transfer from Ce to B6 in the Kondo Crystal CeB6 and Its Mechanism by Multi-Temperature X-Ray Diffraction,” Acta Crystallographica, Vol. B58, 2002, pp. 423-436.
- S. Funahashi, K. Tanaka and F. Iga, “X-Ray Atomic Orbital Analysis of 4f and 5d Electron Configuration of SmB6 at 100, 165, 230 and 298K,” Acta Crystallographica, Vol. B66, 2010, pp. 292-306.
- N. Ogita, S. Nagai, N. Okamoto, F. Iga, S. Kunii, J. Akimitsu and M. Udagawa, “Raman Scattering Study of Hexaboride Crystals,” Physica B, Vol. 328, No. 1-2, 2003, pp. 131-134. http://dx.doi.org/10.1016/S0921-4526(02)01827-6
- D. Yu Chernyshov, M. B. Smirnov, A. V. Menshikova, A. P. Mirogodosky and V. A. Trounov, “Mean Square Displacements of Atoms in Hexaborides,” Physica B, Vol. 234-236, 1997, pp. 146-148. http://dx.doi.org/10.1016/S0921-4526(96)00931-3
- R. D. Shannon, “Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides,” Acta Crystallographica, Vol. A32, 1976, pp. 751-767.
- G. E. Grechnev, A. E. Baranovskiy, V. D. Fil, T. V. Ignatova, N. Yu. Shitsevalova, V. B. Filippov and O. Eriksson, “Electronic Structure and Bulk Properties of MB6 and MB12 Borides,” Low Temperature Physics, Vol. 34, No. 11, 2008, pp. 921-929. http://dx.doi.org/10.1063/1.3009588
- K. Schmitt, C. Stuckl, H. Ripplinger and B. Albert, “Crystal and Electronic Structure of BaB6 in Comparison with CaB6 and Molecular [B6H6]−2,” Solid State Sciences, Vol. 3, 2001, pp. 321-327. http://dx.doi.org/10.1016/S1293-2558(00)01091-8
- G. Mair, H.-G. von Schnering, M. Worle and R. Nesper, “Dilithium Hexaboride, Li2B6,” Zeitschrift für Anorganische und Allgemeine Chemie, Vol. 625, No. 7, 1999, pp. 1207-1211. http://dx.doi.org/10.1002/(SICI)1521-3749(199907)625:7<1207::AID-ZAAC1207>3.0.CO;2-9
- G. Barantseva and B. P. Yu, “Possibility of Existence of Scandium Hexaboride,” Test Methods and Properties of Powder Metallurgical Materials, Plenum Publishing Corp., 1982, pp. 56-60.
- Y. Xu, L. Zhang, T. Cui, Y. Li, Y. Xie, W. Yu, Y. Ma and G. Zou, “First-Principles Study of the Lattice Dynamics, Thermodynamic Properties and Electron-Phonon Coupling of YB6,” Physical Review B, Vol. 76, No. 21, 2007, Article ID: 214103. http://dx.doi.org/10.1103/PhysRevB.76.214103
- K. Shirai and N. Uemura, “Why Does a Metal Get an Insulator? Consequences of Unfilled Bands on Boron Crystals,” Solid State Sciences, Vol. 14, No. 11-12, 2012, pp. 1609-1616. http://dx.doi.org/10.1016/j.solidstatesciences.2012.03.008
- F. Thevenot, “Boron Carbide—A Comprehensive Review,” Journal of the European Ceramic Society, Vol. 6, No. 4, 1990, pp. 205-225. http://dx.doi.org/10.1016/0955-2219(90)90048-K
- I. R. Shein, K. I. Shein, G. P. Shveikin and A. L. Ivanoskii, “Electronic Structure of Cubic Thorium Monocarbide and Hexaboride,” Doklady Physical Chemistry, Vol. 407, No. 2, 2006, pp. 106-109. http://dx.doi.org/10.1134/S0012501606040075
- J. Etourneau, R. Naslain and S. La Placa, “L’Hexaborure de Thorium Non-Stoechiometrique Th1-xB6,” Journal of the Less Common Metals, Vol. 24, No. 2, 1971, pp. 183- 194. http://dx.doi.org/10.1016/0022-5088(71)90095-6
- V. A. Trunov, A. L. Malyshev, D. Yu Chernyshov, A. I. Kurbakov, M. M. Korsukova, V. N. Gurin, L. A. Aslanov and V. V. Chernyshev, “Isotopic Engineering of ‘ZeroMatrix’ Samarium Hexaboride: Results of High-Resolution Powder Neutron Diffraction and X-Ray Single-Crystal Diffratometry Studies,” Journal of Applied Crystallography, Vol. 24, 1991, pp. 888-892. http://dx.doi.org/10.1107/S0021889891001620
- Y. Katsura, A. Yamamoto, H. Ogino, S. Horii, J. Shimoyama, K. Kishio and H. Takagi, “On the Possibility of MgB2-Like Superconductivity in Potassium Hexaboride,” Physica C, Vol. 470, 2010, pp. S633-S634. http://dx.doi.org/10.1016/j.physc.2009.12.067
- D. P. Young, D. Hall, M. E. Torelli, Z. Fisk, J. L. Sarrao, J. D. Thompson, H.-R. Ott, S. B. Oseroff, R. G. Goodrich and R. Zysler, “High-Temperature Weak Ferromagnetism in a Low-Density Free-Electron Gas,” Nature, Vol. 397, 1999, pp. 412-414. http://dx.doi.org/10.1038/17081
- Z. Yahia, S. Turrell, J.-P. Mercurio and G. Turrell, “Spectroscopic Investigation of Lattice Vacancies in Hexaborides,” Journal of Raman Spectroscopy, Vol. 24, No. 4, 1993, pp. 207-212. http://dx.doi.org/10.1002/jrs.1250240405
- B. Jager, S. Paluch, W. Wolf, P. Herzig, O. J. Zogal, N. Shitsevalova and Y. Paderno, “Characterization of the Electronic Properties of YB4 and YB6 Using 11B NMR and First-Principles Calculations,” Journal of Alloys and Compounds, Vol. 383, No. 1-2, 2004, pp. 232-238. http://dx.doi.org/10.1016/j.jallcom.2004.04.067
- A. M. Gabovich, A. I. Voitenko and M. Ausloos, “Chargeand Spin-Density Waves in Existing Superconductors: Competition between Cooper Pairing and Peierls or Excitonic Instabilities,” Physics Reports, Vol. 367, 2002, pp. 583-709. http://dx.doi.org/10.1016/S0370-1573(02)00029-7
- B. Albert and K. Schmitt, “New Boron-Rich Materials: Cubic Carbaborides of Sodium and Potassium,” Chemistry of Materials, Vol. 11, No. 11, 1999, pp. 3406-3409. http://dx.doi.org/10.1021/cm991130d

