Journal of Geoscience and Environment Protection
Vol.06 No.06(2018), Article ID:85719,17 pages
10.4236/gep.2018.66011
Analytical Hierarchy (AHP) Process Method for Environmental Hazard Mapping for Jeddah City, Saudi Arabia
Ahmad Almodayan
Department of Geography and GIS, King Abdulaziz University, Jeddah, Kingdom of Saudi Arabia
Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 19, 2018; Accepted: June 26, 2018; Published: June 29, 2018
ABSTRACT
The city of Jeddah, the second major city in the Kingdom of Saudi Arabia (KSA), was severely damaged on November 25, 2009. A deadly and costly flash flood, which can be exacerbated in arid environments, occurred when more than 90 millimetres (3.5 inches) of rain fell in just four hours. A national disaster was declared. This extreme disaster has been a catalyst for attempts to advance our understanding of flash flood events and how to appropriately respond to their destructive nature. One-hundred and twenty people were killed, around 350 others were reported missing and approximately four billion Saudi riyals (one billion US dollars) of damage was caused. Considered to be one of the great of Saudi’s cities, Jeddah is the economic capital of the country. It is the largest coastal town on the west coast, with a population of about 5.1 million and an estimated area of 5460 square kilometres. Based on its rapid urbanisation and population growth, a function of a multitude of parameters, a multi-criterion analysis using AHP and GIS was performed to comprehensively evaluate the environmental quality of the different municipal wards affected by Jeddah’s flash floods. This research presents an analysis of the different factors that caused these flash flood events. The results indicate that the causes of these floods are related to a number of factors that significantly contribute to the worsening of flood disasters.
Keywords:
Flash Floods, GIS, AHP, Hazards, Jeddah

1. Introduction
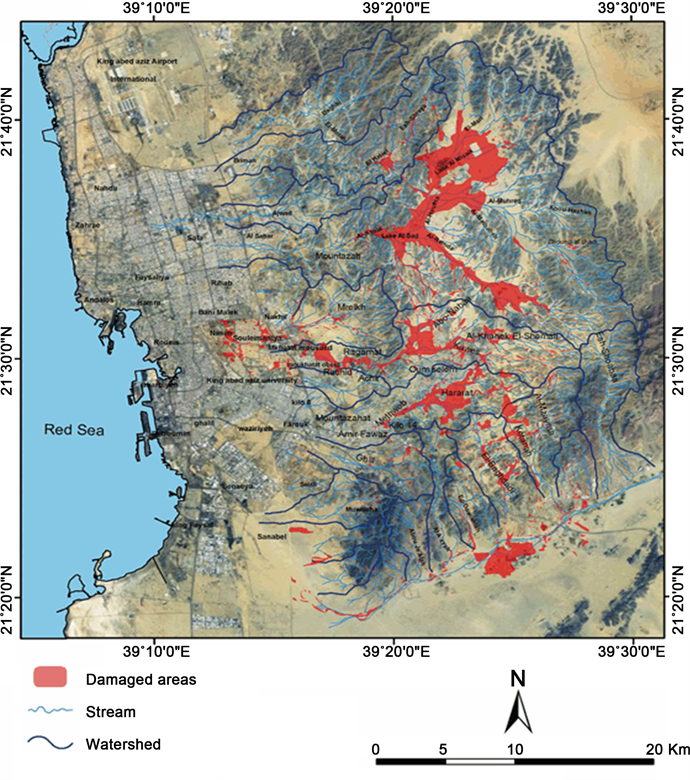
On November 25, 2009, a heavy rainstorm hit the city of Jeddah (see Figure 1 & Figure 2), the second largest city in the Kingdom of Saudi Arabia. It produced a flash flood, in only a small period of time, causing at least 122 fatalities, more than 1000 injuries and around 350 people to be reported missing. Unhelpfully, the only available rainfall data were limited to the weather station at King Abdulaziz International airport, north of the city, while the most extreme precipitation occurred over its southern part. Nevertheless, even though they do not reflect the true severity of the event these data were used to compare the simulation results.
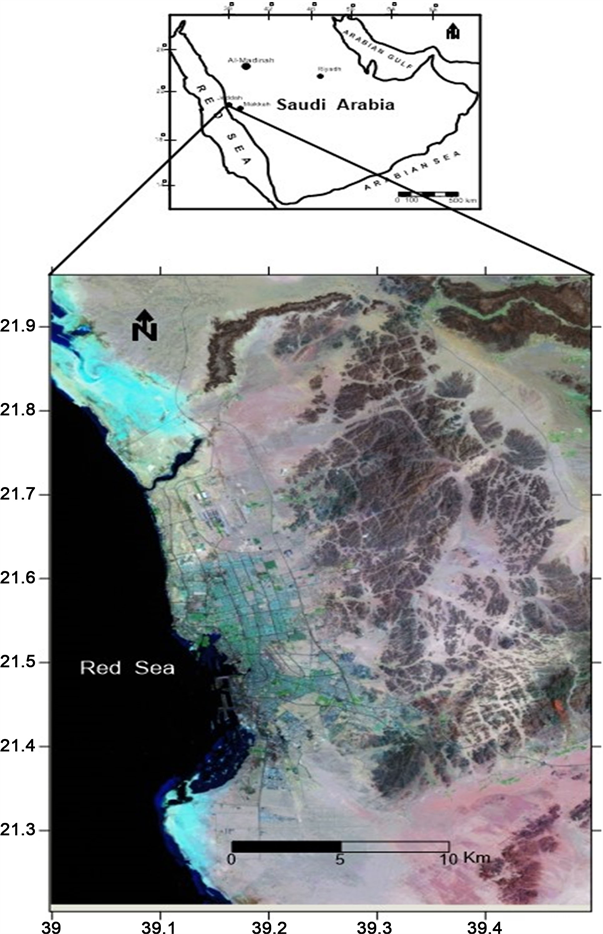
Jeddah is the economic capital of the country, with a population of about 5.1 million and covering an estimated area of 5460 square kilometres as shown in Figure 1. It lies on approximately the middle part of the Red Sea shore of Saudi
Figure 1. Location of study area.
Figure 2. Flooding event in Jeddah from November 2009.
Arabia, occupying a stretch of land 60 km long and 40 km wide. It is bound by latitudes 21˚15'00"N and 21˚55'00"N, and longitudes 39˚00'00”E and 39˚30'00"E. The great majority of the drainage systems in the area are directed towards the west; at the extreme eastern part of the area, few systems are directed towards the east, and those that are have been ignored in this study.
A city of the Kingdom of Saudi Arabia, Jeddah (our study area) is considered the economic capital of the country. It is the largest seaport on the west coast, with a population of about 5.1 million and covering an estimated area of 5460 square kilometers. It is an all-year round destination for many Saudi tourists because of its reputation as businesses and finance hub, as well as the availability of merchandise and goods. Jeddah is the principal gateway to Makkah. Located 80 km to the east, Makkah is Islam’s holiest city, which Muslims are required to visit at least once in their life to perform a pilgrimage. Jeddah is classified climatically, according to the World Map of the Köppen-Geiger climate classification [1] , as a semi-arid region. Such climates tend to be hot, sometimes extremely hot, during summer and mild to warm during winter.
Most of Jeddah’s annual rainfall typically arrives in the form of a few intense thunderstorm events of relatively short duration during the wet season. Annual precipitation is reported to be around 52.5 mm/year; a maximum rainfall of 284 mm occurred in 1996. Subyani (2009) has indicated that in addition to seasonal variation, rainfall and temperature vary in response to changes in physiography across Jeddah and the surrounding region as shown in Figure 2.
The climate of the Jeddah Governate is a hot, arid, desert type, with scarce rainfalls in the spring season. According to ten years of records, held by the Ministry of Defence and Aviation [2] covering the period between 1990 and 1999, the temperature reaches a maximum of 49˚C during the period between March and August, and a minimum of 17.3˚C in the period between January and February. Relative humidity ranges between a maximum of 100% in the period between August to November, and a minimum of 5% during January and March. The precipitation rate is about 55 mm/year. Subyani [3] reported that rainfall values are generally low in the narrow coastal plain region, increasing with increasing elevation in the foothills and mountain regions. Similarly, temperature generally follows an inverse relation with elevations, with higher temperatures in the coastal plain region decreasing with increasing elevation in the foothills and mountain regions. The Jeddah area is characterised by a number of wadis that run into the shallow coastal waters and which carry sufficient sand and mud to deposit large inshore aprons of soft sediments. These drainage systems have dissect the Jeddah area and are characterised by high gradients [4] .
Natural disasters are considered the main cause of irrevocable damage worldwide [5] . Saudi Arabia experiences flood events annually in different areas [6] . Many researchers have observed a relationship between land use changes and flood hazard using GIS-based analysis, such as Chang [7] , while others have applied RS and GIS in different types of hydrological studies [8] [9] [10] [11] .
A number of studies have been conducted analysing the severe storm that occurred in Jeddah on November 25, 2009 [12] [13] . The heavy rainfall caused by this severe storm event resulted in large economic losses and loss of life. If such phenomena can be better understood, then future events might be better predicted.
Conversely, some researchers have studied flood risk and flood damage estimates using partial multi-criterion analysis, geographic information systems (GIS) and mathematical models [14] [15] [16] [17] , presenting information on flood risk in diverse spatial locations in order to develop effective flood prevention strategies and damage estimates for crisis situations. Industrial engineering applications of the Analytic Hierarchy Process (AHP) include its use in integrated manufacturing [18] , the evaluation of technology investment decisions [19] , layout design [20] and other engineering problems [21] .
2. Analytic Hierarchy Process (AHP)
Analytic Hierarchy Process [22] [23] is a multi-criterion, decision-making method. It is a very flexible and powerful tool because its scores, and therefore its final ranking, are obtained on the basis of pairwise relative evaluations of both the criteria and the options provided by the user. In short, it is a method for deriving ratio scales from paired comparisons. The input can be obtained from actual measurements, such as price, weight etc., or from subjective opinion such as feelings of satisfaction and preference. Because humans are not always consistent, AHP allows for some inconsistency in judgment. The ratio scales are derived from the principal Eigen vectors, the consistency index from the principal Eigen value.
The nominal scale is applied to paired comparisons among factors so that uncountable human feelings and preference can be quantified, and the paired comparison matrix is established for the eigenvector for the priority. It presents the characteristics of structure, complex scale, rational paired comparison and integrated opinions of different decision-makers with weighted average value.
The AHP considers a set of evaluation criteria and a set of alternative options from which the best decision is to be made. It is important to note that, since some of the criteria might be conflicting, it is generally not true that the best option is the one that optimises each single criterion, but rather it is the one that achieves the most suitable trade-off among the different criteria.
The AHP generates a weighting for each evaluation criterion according to the decision-maker’s pairwise comparisons of the criteria. The higher the weighting, the more important the corresponding criterion. Next, for a fixed criterion the AHP assigns a score to each option, according to the decision-maker’s pairwise comparisons of the options based on that criterion. The higher the score, the better the performance of the option with respect to the criterion considered. Finally, the AHP combines the criteria weightings and the options scores, thus determining a global score and a consequent ranking for each option. The global score for a given option is the weighted sum of the scores obtained with respect to all the criteria.
The AHP is a very flexible and powerful tool because the scores, and therefore the final ranking, are obtained on the basis of pairwise relative evaluations of both the criteria and the options provided by the user. The computations made by the AHP are always guided by the decision-maker’s experience, and thus the AHP can be considered a tool that is able to translate evaluations (both qualitative and quantitative) made by the decision-maker into a multi-criterion ranking. In the AHP every single evaluation is very simple since it only requires the decision-maker to express how two options or criteria compare with each other, the load of the evaluation task may become unreasonable. In fact, the number of pairwise comparisons grows quadratically with the number of criteria and options.
The AHP can be implemented in three simple consecutive steps: 1) weight of the criteria vector, 2) matrix of option scores, 3) ranking of options.
Each step is described in detail in the following section. It is assumed that m evaluation criteria will be considered and n options evaluated. A useful technique for checking the reliability of the results will also be introduced.
To calculate the weights for the different criteria, the AHP starts by creating a pairwise comparison matrix B (m×m), where m is the number of evaluation criteria considered. Each element bjk of the matrix B represents 1, the importance of the jth criterion relative to the kth criterion. If bjk > 1, then the jth criterion is more important than the kth criterion, whereas if bjk < 1, then the jth criterion is less important than the kth criterion.
If two criteria have the same importance, then the entry bjk is 1. The entries bjk and bkj satisfy the following constraint:
Then, we formalise the normalised pairwise comparison matrix Bnorm, where the elements of the matrix are as follows;
And the criteria weight vector w is calculated as:
In the matrix of option scores, the matrix of option scores is n × m real matrix Q. Each entry qij of Q represents the score of the ith option with respect to the jth criterion. Finally, the score matrix Q is obtained, as follows:
i.e. the jth column of Q corresponds to q(j).
In the ranking of options, once the weight vector w and the score matrix Q have been computed, the AHP obtains a vector v of global scores by multiplying Q and w, i.e.
The ith entry vi of v represents the global score assigned by the AHP to the ith option. As the final step, the option ranking is accomplished by ordering the global scores in decreasing order.
2.1. Flood Risk General Procedure
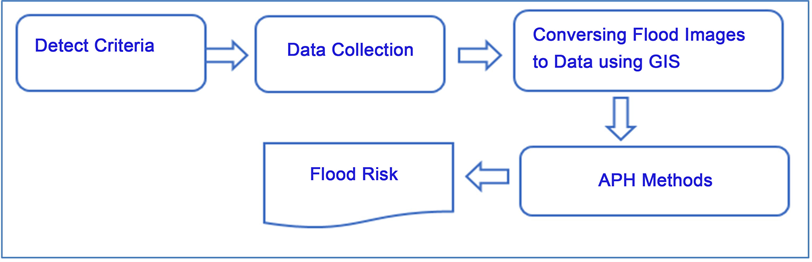
Figure 3 summarises the methodology used. Following selection of the study area, spatial data such as land use/land cover map and discharge time series measured at hydrometric stations, were collected. Data from the disaster area in Jeddah included images, excel sheets, and so on. We then used GIS systems to convert the images to data based on the requirements of the APH method. As shown in Figure 4, these risk area data were then assigned by experts to the following categories: very high, high, moderate, low, very low. The APH analysis integrates the spatial data in order to describe the causal factors of the phenomenon under investigation. Based on expert opinion and the data available, the danger areas were initially generated by numerically overlaying soil, drainage network, and slope and rainfall layers.
Figure 3. Methodology of the proposed system.
Figure 4. General procedure undertaken to develop flood risk map in GIS for the study area.
In a second phase, each criterion was sorted according to the decision-maker’s preference. Each factor was weighted according to its estimated significance for causing flooding. Inverse ranking was applied to these factors, with a factor of rank one being the least important and one of rank eight the most important. In the third phase the pairwise comparison method, developed by Saaty [23] , was used to determine the weight of each criterion.
3. Results and Discussion
The dataset contains the volume of rainfall from 1971 into 2012 for Jeddah City. As shown in Table 1 and Figure 5, the highest volume of rainfall occurred in 1991 and was around three times that recorded in the disaster year, 2009.
The reasons for the flood were that more than 70 millimetres (2.76 inches) of rain fell in Jeddah in just four hours on Wednesday, 25 November. This was two days before the Eid al-Adha anniversary, at a time when no-one expected such a large volume of rainfall to occur. The rainfall hit the poorer areas to the south of Jeddah, as was well as the area around King Abdulaziz University?thankfully, the university was closed for the holiday period, thus avoiding even higher numbers of victims.
Various factors can cause flash floods, including natural factors such as heavy monsoon rainfall, intense convection rainstorms and poor drainage, coupled with geomorphological, geological and anthropogenic factors.
3.1. Hierarchic Structure of Risk Analysis
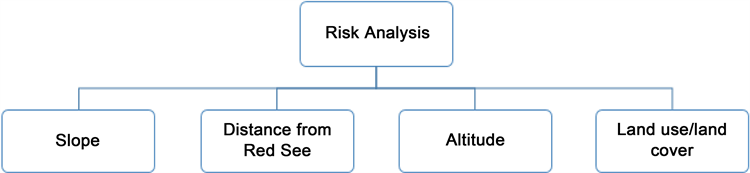
Figure 6 shows preliminary factor structure for the compound potential hazard
Table 1. Data set of the rainfall in jeddah area rainfall.
Figure 5. Average of rainfall in Jeddah.
Figure 6. Hierarchic structure of risk analysis.
analysis, with classified levels from between 0 into 10 based on expert advice. Relevant flood potential factors, such as slope percent, distance from the Red Sea, altitude and land use/land cover and, were selected. All these factors were converted into a raster grid with 30 by 30 m cells according to the AHP method.
The rapid expansion of Jeddah city has caused a significant alteration of wadies that run through the city towards the red sea. The current situation of Jeddah wadies made this research focus on presenting the impact of the slope, distance from the sea, altitude, and land use on flood potential.
The HEC-RAS model was used to simulate flood depth and extend areas for peak discharges of 1510 mm (50-year return period) and 1670 mm (100-year return period). Table 2 show the matrix of the relative importance of evaluated items in the risk analysis.
Figure 7 shows the weights for all nodes of the hierarchy. As can be seen, land use zoning has the most significant weight (40%), slope the least (8%).
After computing the weights for the all nodes of the hierarchy, we find the followings results.
Table 2. Pair-wise comparison matrix and normalized weights for parameters.
Figure 7. Weights after computing analytic hierarchy process.
3.1.1. Slope Class
Youssef et al. [24] considers slope percentage to be a surface indicator of flood susceptibility. Slope plays a significant part in determining surface runoff velocity and vertical percolation, thus affecting flood exposure. Table 3 shows the assigned and normalized ranks for Slope class and Figure 8 shows the slope map for Jeddah, produced using ArcGIS 10.5.
Climatic factors combined with the erosion activity watercourses and groundwater are significant causes of slope deformations. In 2009 as a result of exceptionally heavy rainfall, the flood situation increased the number of slope deformations on some areas of Jeddah which made it necessary to have to calculate slope stability. Zhang et al. [25] presented in what way site-specific information on survival of loads a dyke was subjected to can be used for reliability updating with slope stability. A proposed methodology to investigate the effect of land-use/land-cover change on a slope and its stability by [26] . The objectives of this method are: 1) to identify the controlling factors of different types of slope movement, 2) to investigate to what extent the inclusion of spatially distributed
Table 3. Assigned and normalized ranks for slope class.
Figure 8. Slope class based on ArcGIS 10.5.
land-use data in a physically based slope stability model improves the prediction of slope movement patterns, and 3) to investigate the effect of past and future land-use change on slope movement susceptibility.
3.1.2. Distance from the Red Sea
Flood areas are at greater risk when they are close to a sea or river. Such areas are generally considered to have flood potential and must therefore be considered in future risk management policies. Table 4 shows the assigned and normalized ranks for Distance from the red see class. The map in Figure 9 was produced using the buffer tool in ArcGIS 10.5 software, revealing five buffer categories. The distance intervals used were: 0 - 20; 20 - 80; 80 - 140 and >140 km.
3.1.3. Altitudes Class
In accordance with Stieglitz et al. [27] , we included altitude in our calculations because it has a significant impact on the spread of flooding in the study area.
Table 4. Assigned and normalized ranks for distance from the red see class.
Figure 9. Distance from the sea class based on ArcGIS 10.5.
Table 5 shows the assigned and normalized ranks for Altitudes class. Stieglitz [27] considered altitude a very important factor in the control of both the overflow direction movement and the depth of the flood.
The altitude map of the Jeddah area was produced from ASTER DEM images of the area using ArcGIS 10.5 software, as shown in Figure 10. It was grouped into five classes, as follows: 0 - 100; 100 - 200; 200 - 1000; 1000 - 2000 and >1000 - 2000, representing classes 1 to 5 respectively.
3.1.4. Land Use/Land Cover
Norman et al. [28] considered land use/land cover to be vital in classifying those
Table 5. Assigned and normalized ranks for altitudes class.
Figure 10. Altitudes class based on ArcGIS 10.5.
zones shown to have high exposure to flooding. Figure 11 shows the Jeddah map with three land use classes: residential areas, bare land and rock zone. Bare land areas have low potential for flooding due to the negative relationship between flooding and bare land. Conversely, residential areas and rock zones have potential flood risk with a normalized rank of 0.5454 and 0.2727 respectively. Table 6 shows the assigned and normalized ranks for Land use/land cover class.
4. Conclusion
This paper presents an analysis of GIS images of the disaster that occurred in Jeddah in 2009. Based on rapid urbanisation and population growth, which is a function of multiple parameters, a multi-criterion analysis was performed using
Figure 11. Land use/land cover class based on ArcGIS 10.5.
Table 6. Assigned and normalized ranks for land use/land cover class.
AHP and GIS in order to produce a comprehensive evaluation of the environmental quality of different municipal flood wards. This research presents an analysis of the different factors that caused these flash flood events. Several types of disasters were categorised using questionnaires and the data sent to experts along with a survey to formulate a weight analysis. To complete the analysis, the experts selected four factors of flood potential; slope percent, distance from the Red Sea, altitude and land use/land cover. Four maps of the Jeddah area were produced from ASTER DEM images of the area using ArcGIS 10.5 software. For example, the map classified land use/land cover class into three subclasses: residential, rock and bare land zones, with a potential flood risk of normalized rank 55%, 27% and 18% respectively. Such results could prove useful for those working in disaster prevention. The results indicate that the causes of these floods are related to a number of factors that contribute greatly to the worsening of flood disasters.
Cite this paper
Almodayan, A. (2018) Analytical Hierarchy (AHP) Process Method for Environmental Hazard Mapping for Jeddah City, Saudi Arabia. Journal of Geoscience and Environment Protection, 6, 143-159. https://doi.org/10.4236/gep.2018.66011
References
- 1. Peel, M.C., Finlayson, B.L. and McMahon, T.A. (2007) Updated World Map of the Köppen-Geiger Climate Classification. Hydrology and Earth System Sciences, 11, 1633-1644.
- 2. Ministry of Defense and Aviation (1999) Provisional Normals (10 Years) from 1990 to 1999, Meteorology and Environmental Protection Administration, Scientific Information and Documentation Center, Kingdom of Saudi Arabia.
- 3. Subyani, A.M. (2009) Hydrologic Behaviour and Flood Probability for Selected Arid Basins in Makkah Area, Western Saudi Arabia. Arabian Journal of Geosciences, 4, 817-824.
- 4. Qari, M.H.T. (2009) Geomorphology of Jeddah Governorate, with Emphasis on Drainage Systems. Journal of King Abdulaziz University, 20, 93-116.
- 5. Vorogushyn, S., Lindenschmidt, K.E., Kreibich, H., Apel, H. and Merz, B. (2012) Analysis of a Detention Basin Impact on Dike Failure Probabilities and Flood Risk for a Channel-Dike-Floodplain System along the River Elbe, Germany. Journal of Hydrology, 436, 120-131.
- 6. Youssef, A.M. and Maerz, H.N. (2013) Overview of Some Geological Hazards in the Kingdom of Saudi Arabia. Environmental Earth Sciences, 70, 3115-3130.
- 7. Chang, H., Franczyk, J. and Kim, C. (2009) What Is Responsible for Increasing Flood Risks? The Case of Gangwon Province, Korea. Natural Hazards, 48, 339-354. https://doi.org/10.1007/s11069-008-9266-y
- 8. Youssef, A.M. and Hegab, M.A. (2005) Using Geographic Information Systems and Statistics for Developing a Database Management System of the Flood Hazard for Ras Gharib Area, Eastern Desert, Egypt. The Fourth International Conference on the Geology of Africa; 15-17 November 2005, Assiut University, Assiut (EG), Vol. 2, 1-15.
- 9. Bates, P.D. (2012) Integrating Remote Sensing Data with Flood Inundation Models: How Far Have We Got? Hydrological Process, 26, 2515-2521.
- 10. Wanders, N., Bierkens, M.F., de Jong, S.M., de Roo, A. and Karssenberg, D. (2013) The Benefits of Using Remotely Sensed Soil Moisture in Parameter Identification of Large-Scale Hydrological Models. EGU General Assembly Conference Abstracts, 7-12 April 2013, Vienna, Vol. 15, 10215.
- 11. Wanders, N., Karssenberg, D., de Roo, A., de Jong, S.M. and Bierkens, M.F.P. (2014) The Suitability of Remotely Sensed Soil Moisture for Improving Operational Flood Forecasting. Hydrology and Earth System Sciences, 18, 2343-2357.
- 12. AlKhalaf, A. and Basset, H.A. (2013) Diagnostic Study of a Severe Thunderstorm over Jeddah. Atmospheric and Climate Sciences, 3, 150-164. https://doi.org/10.4236/acs.2013.31017
- 13. Haggag, M. and El-Badry, H. (2013) Mesoscale Numerical Study of Quasi-Stationary Convective System over Jeddah in November 2009. Atmospheric and Climate Sciences, 3, 76-86. https://doi.org/10.4236/acs.2013.31010
- 14. Raaijmakers, R., Krywkow, J. and van der Veen, A. (2008) Flood Risk Perceptions and Spatial Multi-Criteria Analysis: An Exploratory Research for Hazard Mitigation. Natural Hazards, 46, 307-322. https://doi.org/10.1007/s11069-007-9189-z
- 15. Karmakar, S., Simonovic, S., Peck, A. and Black, J. (2010) An Information System for Risk-Vulnerability Assessment to Flood. Journal of Geographic Information System, 2, 129-146. https://doi.org/10.4236/jgis.2010.23020
- 16. Moel, H. and Aerts, J.C.J.H. (2011) Effect of Uncertainty in Land Use, Damage Models and Inundation Depth on Flood Damage Estimates. Natural Hazards, 58, 407-425. https://doi.org/10.1007/s11069-010-9675-6
- 17. Gharagozlou, A., Nazari, H. and Seddighi, M. (2011) Spatial Analysis for Flood Control by Using Environmental Modeling. Journal of Geographic Information System, 3, 367-372. https://doi.org/10.4236/jgis.2011.34035
- 18. Putrus, P. (1990) Accounting for Intangibles in Integrated Manufacturing (Nonfinancial Justification Based on the Analytical Hierarchy Process). Information Strategy, 6, 25-30.
- 19. Boucher, T.O. and McStravic, E.L. (1991) Multi-Attribute Evaluation within a Present Value Framework and Its Relation to the Analytic Hierarchy Process. The Engineering Economist, 37, 55-71. https://doi.org/10.1080/00137919108903055
- 20. Cambron, K.E. and Evans, G.W. (1991) Layout Design Using the Analytic Hierarchy Process. Computers & IE, 20, 221-229.
- 21. Wang, L. and Raz, T. (1991) Analytic Hierarchy Process Based on Data Flow Problem. Computers & IE, 20, 355-365.
- 22. Saaty, T.L. (1980) The Analytic Hierarchy Process. McGraw-Hill Press, New York.
- 23. Saaty, T.L. (1990) Decision Making for Leaders—The Analytic Hierarchy Process for Decisions in a Complex World. RWS Publications Press, Pittsburgh.
- 24. Youssef, A.M., Pradhan, B. and Hassan, A.M. (2011) Flash Flood Risk Estimation along the St. Katherine Road, Southern Sinai, Egypt Using GIS Based Morphometry and Satellite Imagery. Environmental Earth Sciences, 62, 611-623.
- 25. Zhang, J., Zhang, L.M. and Tang, W.H. (2011) Slope Reliability Analysis Considering Site-Specific Performance Information. Journal of Geotechnical and Geoenvironmental Engineering, 137, 227-238. https://doi.org/10.1061/(ASCE)GT.1943-5606.0000422
- 26. Vanacker, V., Vanderschaeghe, M., Govers, G., Willems, E., Poesen, J., Deckers, J. and De Bievre, B. (2003) Linking Hydrological, Infinite Slope Stability and Land-Use Change Models through GIS for Assessing the Impact of Deforestation on Slope Stability in High Andean Watersheds. Geomorphology, 52, 299-315. https://doi.org/10.1016/S0169-555X(02)00263-5
- 27. Stieglitz, M., Rind, D., Famiglietti, J. and Rosenzweig, C. (1997) An Efficient Approach to Modeling the Topographic Control of Surface Hydrology for Regional and Global Climate Modeling. Journal of Climate, 10, 118-137.
- 28. Norman, L.M., Huth, H., Levick, L., Burns, I.S., Phillip Guertin, D., Lara-Valencia, F. and Semmens, D. (2010) Flood Hazard Awareness and Hydrologic Modelling at Ambos Nogales, United States, Mexico Border. Flood Risk Management, 3, 151-165.