Journal of Geoscience and Environment Protection
Vol.04 No.02(2016), Article ID:63798,15 pages
10.4236/gep.2016.42011
Groundwater Quality Evaluation Using GIS Based Geostatistical Algorithms
Abdalkarim S. Gharbia1*, Salem S. Gharbia2,3, Thaer Abushbak1,4, Hisham Wafi1, Adnan Aish1, Martina Zelenakova5, Francesco Pilla3
1Institute of Water and Environment, Al-Azhar University, Gaza, Palestine
2Department of Water Resources and Planning, Palestinian Water Authority, Gaza, Palestine
3Department of Civil, Structural and Environmental Engineering, Trinity College, Dublin, Ireland
4Ministry of Agriculture, Gaza, Palestine
5Institute of Environmental Engineering, Technical University of Kosice, Kosice, Slovakia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 January 2016; accepted 22 February 2016; published 25 February 2016
ABSTRACT
Groundwater quality is a major environmental aspect which needs to be analyzed and managed depending on its spatial distribution. Utilization of insufficient management of groundwater resources in Gaza Strip, Palestine, produces not only a reduction in quantity but also deterioration in quality of groundwater. The aim of this study is to provide an overview for evaluation of groundwater quality in the Gaza Strip area as a case study for applying spatially distributed by using Geographic Information System (GIS) and geostatistical algorithms. The groundwater quality parameters, pH, total dissolved solids, total hardness, alkalinity, chloride, nitrate, sulfate, calcium, magnesium, and fluoride, were sampled and analyzed from the existing municipal and agricultural wells in Gaza Strip; maps of each parameter were created using geostatistical (Kriging) approach. Experimental semivariogram values were tested for different ordinary Kriging models to identify the best fitted for the ten water quality parameters and the best models were selected on the basis of mean square error (MSE), root mean square error (RMSE), average standard error (ASE), and root mean square standardized error (RMSSE). Maps of 10 groundwater quality parameters were used to calculate the groundwater quality index (GWQI) map using the index method. In general, the results showed that this integrated method is a sufficient assessment tool for environmental spatially distributed parameters.
Keywords:
Groundwater, Water Quality, GIS, Geo-Statistics

1. Introduction
Nearly three billion people live without access to adequate sanitation systems necessary for reducing exposure to water-related diseases. The failure in solving this crisis leads to poor water quality in natural water resources especially groundwater [1] [2] . Gaza Strip faces both groundwater quality and quantity issues as the considerable amount of water demand is fulfilled from groundwater. Increasing in population, urban development, and agriculture are just some of the factors which have an impact on the water quality in this area. In addition, climate changes have severe negative impacts on groundwater of the Gaza coastal aquifer [3] -[5] .
Many researchers applied geostatistical approach for analysis of spatial variations of groundwater characteristics [6] -[9] . The measurement of pollutant concentration at all location is not always possible from time and cost perspectives in data collection stage [10] . Therefore, prediction of values at other locations based upon selectively measured values represents a viable alternative. In this case, to predict the concentration of pollutants at unmeasured locations, the geostatistical techniques can be used [11] . The basic idea in using geostatistics is that the characteristics of earth have some spatial continuity up to a certain lag distance. The geostatistical concepts and its applications are reported by different researchers around the world. Kriging method theorizes the spatial correlation between the sample points. Kriging is mostly used for mapping spatial variability [12] . Kriging is a special case from IDW and other interpolation methods by taking into consideration the difference of estimated parameters. Geostatistical approach and Kriging methods have several advantages, such as giving fair predictions with minimum variance and taking the spatial correlation between the data listed at various places. On the other hand, Kriging gives information on interpolation errors about the reliability of estimates [13] -[15] .
Many researches depend on evaluation the groundwater quality on calculating Water Quality Index [16] -[20] . The Water Quality Index (WQI) is considerably used to appreciate the convenience of surface water as well as groundwater for drinking, domestic and agriculture purposes. Generally, the WQI and Geographic Information System (GIS) are used to evaluate and map the spatial distribution of groundwater quality. The previous groundwater quality studies in Gaza Strip [21] [22] show that groundwater recharge zones are represented as points and are used as sources for transportation of contaminant to groundwater. Groundwater quality maps are dynamic for identifying locations that are involved in groundwater contamination [23] .
The area that will be studied on this paper is Gaza Strip, which is a part of the Palestinian coastal flat located in an arid to semi-arid region. It is surrounded by Egypt from the south, the green line from the North, Nagev desert from the East and the Mediterranean Sea from the West. Gaza Strip is located on the south-eastern coast of the Mediterranean Sea, between longitudes 34˚20" and 34˚25" east, and latitudes 31˚16" and 31˚45" north (Figure 1). The total surface area of the Gaza Strip is 360 km2, where about 1.8 million Palestinian people live and work. Gaza Strip is classified as one of the most densely populated areas in the world. The Gaza Strip is divided geographically into five governorates: Northern, Gaza, Mid Zone, Khanyounis and Rafah as shown in Figure 1 [1] [3] [24] [25] . The coastal aquifer is the only aquifer in the Gaza Strip and is composed of Pleistocene marine sand and sandstone, intercalated with clayey layers. The maximum thickness of the different bearing horizons occurs in the northwest along the coast (150 m) and decreases gradually toward the east and southeast along the eastern border of Gaza Strip to less than 10 m. The base of coastal aquifer system is formed of impervious clay shade rocks of Neogene age (Saqiyah formation) [26] (see Figure 1). The total groundwater use in year 2012 was about 182 million cubic meters per year (Mm3/year), of which the agricultural use was approximately 87.5 Mm3/year, domestic and industrial consumption about 94.5 Mm3/year. The groundwater level ranges from 18 m below mean sea level (msl) to about 4 m above mean sea level [3] -[5] [24] [25] [27] -[29] .
The main aim of this study is to assess and evaluate groundwater quality for parameters such as pH, TDS, total hardness, alkalinity, chloride, nitrate, sulfate, calcium, magnesium, and fluoride levels by using a GIS based geostatistical algorithms and water quality index in the study area.
In this study, the calculation of geostatistics and groundwater quality index was based on the following 10 water quality parameters: pH, Total Dissolved Solid (TDS), Total Hardness, Alkalinity, and Chloride, Nitrate, Sulfate, Calcium, Magnesium, and Fluoride. Parameters were chosen according to many factors, such as the significance of the parameter and the availability of data. Chloride (Cl−) and TDS selection was related to the high concentration on groundwater; additionally, they are index for salinity, and there effects on human health. As for Nitrate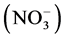 , it is one of the major parameters that affects human health. Finally, Ca, Mg and SO4 are related to agricultural activities. The Ca+ and Mg+ cations are indexes for groundwater hardness, and the high content of these cations in water may affect its acceptability to the consumers in terms of taste and scale deposition. High
, it is one of the major parameters that affects human health. Finally, Ca, Mg and SO4 are related to agricultural activities. The Ca+ and Mg+ cations are indexes for groundwater hardness, and the high content of these cations in water may affect its acceptability to the consumers in terms of taste and scale deposition. High
Figure 1. Location map of Gaza strip and a typical geological cross section (section A-A) for coastal aquifer [28] [29] .
levels of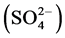 , can cause dehydration and gastrointestinal irritation, and may also contribute to the corrosion of pipes and distribution systems. The high concentration of sewage and industrial waste may be the cause of high alkalinity in the polluted water.
, can cause dehydration and gastrointestinal irritation, and may also contribute to the corrosion of pipes and distribution systems. The high concentration of sewage and industrial waste may be the cause of high alkalinity in the polluted water.
2. Methods and Data
Groundwater samples were collected and analyzed by the Palestinian Water Authority (PWA) and the Ministry of Health (MOH). The samples were collected from 325 groundwater wells during the last three months in the year 2014. The research work described here used this data set, which was provided by PWA and MOH.
2.1. Geostatistical Development Models Approach
Several techniques are available in literature for interpolation, but Kriging methods are the best way for normal distribution data [30] [31] . As such, Kriging was used in this study for spatial variation analysis. Kriging method has three steps.
2.1.1. Exploratory Data Analysis
Exploratory data analysis was executed to explore data and to check data consistency and uniformity, removing outliers and identifying statistical distribution. The histograms and normal Quantile-Quantile plot (QQ plots) were plotted as shown in Table 1 to check the normality of the observed data. Histogram and QQ Plot analy-


Table 1.Histogram and Q-Q plots for groundwater quality parameters.
sis were executed for each water quality parameter and it was found that all the analyzed parameters pH, total dissolved solid, total hardness, alkalinity, chloride, nitrate, sulfate, calcium, magnesium, and fluoride showed mostly a normal distribution by calculating of mean, median, standard deviation (SD) skewness and kurtosis for each sample (Table 2).
2.1.2. Structural Analysis of Data
Spatial correlation or dependence can be quantified with semivariograms (variograms). Applying Kriging approach with semivariograms model is related to the expected squared difference between paired data values z(x) and z(x + h) to the distance lag h, by which locations are separated [32] -[36] .
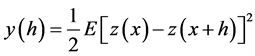 (1)
(1)
For discrete sampling sites the function is written in the form:
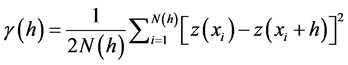 (2)
(2)
where z(xi) is the value of the variable z at location of xi, h is the lag, and N(h) is the number of pairs of sample points separated by h. For irregular sampling, it is rare to be exactly equal to (h). A semivariogram plot is obtained by calculating values of the semivariogram at different lags. The models (circular, spherical, exponential, and Gaussian) provide information about the spatial structure for the Kriging interpolation, the ordinary Kriging method was used in the present study because of its simplicity and prediction accuracy in comparison to other Kriging methods [32] -[36] .
2.1.3. Prediction
Four types of semivariogram models (Circular, Spherical, Exponential, and Gaussian,) were tested for each water quality parameters (pH, TDS, total hardness, alkalinity, chloride, nitrate, sulfate, calcium, magnesium, and fluoride) for the selection of the best one. Predictive performances of the fitted models were checked on the basis of spatial cross validation tests. The values of mean error (ME), mean square error (MSE), root mean error (RMSE), average standard error (ASE) and root mean square standardized error (RMSSE) were estimated to test the performance of the developed models. If the predictions are unbiased, the ME should be near zero. However, this statistic has some important drawbacks: it depends on the scale of the data and is insensitive to inaccuracies in the variogram. So, usually the MSE is used to standardize the ME, being ideally zero, i.e., an accurate model would have a MSE close to zero. In addition to making predictions, each of the Kriging techniques gives the Kriging variances which estimate the variability of the predictions from the known values [32] -[36] .
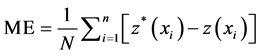 (3)
(3)
Table 2. Descriptive statistics and concentration standards and guidelines of groundwater quality parameters.
 (4)
(4)
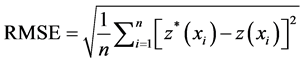 (5)
(5)
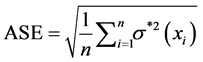 (6)
(6)
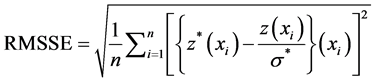 (7)
(7)
where σ*2(xi) is the Kriging variance for location xi. After conducting the cross validation process, maps of kriging estimates were generated which provided a visual representation of the distribution of the water quality parameters.
2.2. Groundwater Quality Index
The Water Quality Index is one of the most effective tools to provide information on the quality of water to the concerned citizens and policy makers. It becomes an important parameter for the assessment and management of groundwater [37] -[40] . The WQI concept is related to the comparison of the water quality parameter with respective regulatory standards (WHO standards) and provides a single number that express overall water quality at certain location based on several water quality parameters [37] -[42] . The WQI summarizes large amount of water quality data into simple terms, i.e., excellent, good, bad, etc., which are easily understandable and usable by the public. However, by combining multiple parameters into a single index, a more comprehensive picture of the pollution state is provided. When mapping the index, the areas of high and low water quality can be easily specified [37] -[42] . The water quality index for the purposes of this study was calculated following three steps. For the first step, a weight (wi) was assigned to each of the ten parameters according to its relative importance in the overall quality of water for drinking [18] . The maximum weight 5 was assigned to nitrate due to its importance on public human health. Magnesium as low harmful has given weight 2. For the second step, the relative weight (Wi) was computed by:
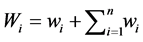 (8)
(8)
where: (Wi) is the relative weight, (wi) is the weight for each parameter and (n) is the number of parameters. For the third step, a quality rating scale (qi) for each parameter was assigned by dividing its concentration in each water sample by its respective standard (WHO standard) [2] and the result was multiplied by 100 to express it in percentage.

where: (qi) is the quality rating, (ci) is the concentration of each pollutant in water sample in mg\L, (Si) WHO standard concentration. For computing the WQI, the Si was determined for each chemical parameter. The sub- index of ith quality parameter can be determined by:


The computed WQI values are classified in to five types as shown in the Table 3.
3. Results and Discussions
3.1. Geostatistical Model
The Kriging variances must be accurately calculated because they have an important influence on some applications of Kriging, e.g., the probability Kriging. If the RMSE is close to the ASE, the prediction errors were correctly assessed. If the RMSE is smaller than the ASE, then the variability of the predictions is overestimated; conversely, if the RMSE is greater than the ASE, then the variability of the predictions is underestimated. The same could be deduced from the RMSSE statistic. It should be close to one. If the RMSSE is greater than one, the variability of the predictions is underestimated; likewise if it is less than one, the variability is overestimated. After conducting the cross validation process, maps of Kriging estimates were generated which provided a visual representation of the distribution of the groundwater quality parameters.
The corresponding sill, nugget, and range values of the best fitted theoretical models were observed and reported in Table 4 and Table 5. The best fitted variogram models are shown in Table 6. Subsequently, thematic maps for groundwater quality parameters were generated using ordinary Kriging.
Table 4 represents characteristics parameters of best fitted semivariogram models for every groundwater quality parameters by check all types of models and chose the best one fitted model in the study area region.
Table 3. Water quality classification based on WQI value.
Table 4. Characteristics parameters of variogram models.
Table 5. Parameters spatial dependence of variogram models.

Table 6.Best-fitted semivariograms models for groundwater quality parameters.
Table 4 shows the best fitted model for each parameter for prediction of pH, TDS, total hardness, alkalinity, chloride, nitrate, sulfate, calcium, magnesium, and fluoride. The ratio of nugget variance to sill expressed in percentages (Table 6) can be used as a criterion for classifying the spatial dependence of groundwater quality parameters. If this ratio is less than 25%, then the variable has a strong spatial dependence; if the ratio is between 25% and 75%, the variable has a moderate spatial dependence and greater than 75%, the variables shows only weak spatial dependence. All parameters of groundwater quality have strong spatial structure. The MSE values were close to zero and their corresponding to RMSSE values close to one represent a good prediction model. Small values of RMSE and ASE for all the ten water quality parameters also show good agreement of the model.
3.2. Spatial Variation of Groundwater Quality Parameters
Spatial distribution of groundwater quality parameters such as pH, TDS, total hardness, alkalinity, chloride, nitrate, sulfate, calcium, magnesium, and fluoride concentrations were carried out using geostatistical techniques in GIS. Ordinary Kriging was used to obtain the spatial distribution of groundwater quality parameters over the area. The distribution maps clearly detect that the water quality levels are poor with respect to the measured quality parameter as shown in Table 7.
3.3. Groundwater Quality Index
Groundwater quality index map was derived from ten water quality parameters. These maps were processed in GIS environment to get the output map (water quality index map) as shown in Figure 2. The ranges and class of the groundwater quality index of WQI map is given in Table 8.
4. Conclusions
Geostatistical analysis techniques, such as Kriging, are considered to be useful techniques for the monitoring, evaluation and management of groundwater resources. This study uses Kriging geostatistical technique and the WQI to map the spatial variability of groundwater quality. The groundwater quality analyses were done for Gaza Strip using GIS based geostatistical algorithm.
Geostatistical analyses (Ordinary Kriging) were carried out for distribution analysis of various water quality
Figure 2. Groundwater quality index map.


Table 7.Spatially distributed maps for groundwater quality parameters.
Table 8. Groundwater quality classes of the final output.
parameters. Results showed that impairment and poor groundwater quality for the Gaza Strip affect directly the people public health. The study illustrates geostatistical techniques for water quality assessment and investigates spatial variations of water quality using WQI as a beneficial tool for the planners and decision makers to devise policy guidelines for efficient management of the groundwater.
Acknowledgements
The authors would like to express the sincere gratitude to Palestinian Water Authority (PWA), Ministry of Agriculture (MOA) and Ministry of Public Health for providing the data for this study.
Cite this paper
Abdalkarim S.Gharbia,Salem S.Gharbia,ThaerAbushbak,HishamWafi,AdnanAish,MartinaZelenakova,FrancescoPilla, (2016) Groundwater Quality Evaluation Using GIS Based Geostatistical Algorithms. Journal of Geoscience and Environment Protection,04,89-103. doi: 10.4236/gep.2016.42011
References
- 1. Gleick, P.H. (1998) The Human Right to Water. Water Policy, 1, 487-503.
http://dx.doi.org/10.1016/S1366-7017(99)00008-2 - 2. Organization, W.H. (2004) Guidelines for Drinking-Water Quality: Recommendations. Vol. 1. World Health Organization, Geneva.
- 3. Gharbia, S.S., Aish, A. and Pilla, F. (2015) Modelling Potential Impacts of Climate Change on Groundwater of the Gaza Coastal Aquifer from Ensemble of Global Climate Model Projections. Civil and Environmental Research, 7, 44-60.
- 4. Gharbia, S.S., Aish, A. and Pilla, F. (2015) Impacts of Climate Change on a Spatially Distributed Water Balance in the Gaza Strip, Palestine. Journal of Environment and Earth Science, 5, 76-91.
- 5. Gharbia, S.S., et al. (2015) Projection of Future Climate by Multi-Model Median Approach under GIS Environment along the Gaza Strip, Palestine. Journal of Environment and Earth Science, 5, 94-104.
- 6. Bjerg, P.L. and Christensen, T.H. (1992) Spatial and Temporal Small-Scale Variation in Groundwater Quality of a Shallow Sandy Aquifer. Journal of Hydrology, 131, 133-149.
http://dx.doi.org/10.1016/0022-1694(92)90215-H - 7. Chien, Y.-J., et al. (1997) Geostatistical Analysis of Soil Properties of Mid-West Taiwan Soils. Soil Science, 162, 291-298.
http://dx.doi.org/10.1097/00010694-199704000-00007 - 8. Wang, Y., Ma, T. and Luo, Z. (2001) Geostatistical and Geochemical Analysis of Surface Water Leakage into Groundwater on a Regional Scale: A Case Study in the Liulin Karst System, Northwestern China. Journal of Hydrology, 246, 223-234.
http://dx.doi.org/10.1016/S0022-1694(01)00376-6 - 9. Ahmadi, S.H. and Sedghamiz, A. (2007) Geostatistical Analysis of Spatial and Temporal Variations of Groundwater Level. Environmental Monitoring and Assessment, 129, 277-294.
http://dx.doi.org/10.1007/s10661-006-9361-z - 10. Kumar, D. and Ahmed, S. (2003) Seasonal Behaviour of Spatial Variability of Groundwater Level in a Granitic Aquifer in Monsoon Climate. Current Science, 84, 188-196.
- 11. Ella, V., Melvin, S. and Kanwar, R. (2001) Spatial Analysis of NO3-N Concentration in Glacial Till. Transactions of the ASAE, 44, 317-327.
- 12. Nayak, T., Gupta, S. and Galkate, R. (2015) GIS Based Mapping of Groundwater Fluctuations in Bina Basin. Aquatic Procedia, 4, 1469-1476.
http://dx.doi.org/10.1016/j.aqpro.2015.02.190 - 13. Jakubek, D.J. and Forsythe, K.W. (2004) A GIS-Based Kriging Approach for Assessing Lake Ontario Sediment Contamination. The Great Lakes Geographer, 11, 1-14.
- 14. Buttner, O., et al. (1998) Special Section-Geochemical and Microbial Processes in Sediments and at the Sediment-Water Interface of Acidic Mining Lakes-Geostatistical Analysis of Surface Sediments in an Acidic Mining Lake. Water Air and Soil Pollution, 108, 297-316.
http://dx.doi.org/10.1023/A:1005145029916 - 15. Büttner, O., Becker, A., Kellner, S., et al. (1998) Geostatistical Analysis of Surface Sediments in an Acidic Mining Lake. Water, Air, and Soil Pollution, 108, 297-316.
http://dx.doi.org/10.1023/A:1005145029916 - 16. Liou, S.-M., Lo, S.-L. and Wang, S.-H. (2004) A Generalized Water Quality Index for Taiwan. Environmental Monitoring and Assessment, 96, 35-52.
http://dx.doi.org/10.1023/b:emas.0000031715.83752.a1 - 17. Bhargava, D.S. (1983) Use of Water Quality Index for River Classification and Zoning of Ganga River. Environmental Pollution Series B, Chemical and Physical, 6, 51-67.
http://dx.doi.org/10.1016/0143-148X(83)90029-0 - 18. Ramakrishnaiah, C., Sadashivaiah, C. and Ranganna, G. (2009) Assessment of Water Quality Index for the Groundwater in Tumkur Taluk, Karnataka State, India. Journal of Chemistry, 6, 523-530.
http://dx.doi.org/10.1155/2009/757424 - 19. Vollenweider, R.A., Giovanardi, F., Montanari, G. and Rinaldi, A. (1998) Characterization of the Trophic Conditions of Marine Coastal Waters, with Special Reference to the NW Adriatic Sea: Proposal for a Trophic Scale, Turbidity and Generalized Water Quality Index. Environmetrics, 9, 329-357.
http://dx.doi.org/10.1002/(SICI)1099-095X(199805/06)9:3<329::AID-ENV308>3.0.CO;2-9 - 20. Cude, C.G. (2001) Oregon Water Quality Index: A Tool for Evaluating Water Quality Management Effectiveness. Journal of the American Water Resources Association, 37, 125-137.
- 21. Basem, S., Sami Abu, F. and Alfred, Y. (2010) Assessment of Groundwater Quality in the Gaza Strip, Palestine Using GIS Mapping. Journal of Water Resource and Protection, 2, 93-104.
- 22. Mogheir, Y. and Singh, V. (2002) Application of Information Theory to Groundwater Quality Monitoring Networks. Water Resources Management, 16, 37-49.
http://dx.doi.org/10.1023/A:1015511811686 - 23. Ganeshkumar, B. and Jaideep, C. (2012) Groundwater Quality Assessment Using Water Quality Index (WQI) Approach—Case Study in a Coastal Region of Tamil Nadu, India. International Journal of Environmental Sciences and Research, 1, 50-55.
- 24. Vengosh, A., Kloppmann, W., Marei, A., et al. (2005) Sources of Salinity and Boron in the Gaza Strip: Natural Contaminant Flow in the Southern Mediterranean Coastal Aquifer. Water Resources Research, 41, Article ID: W01013.
- 25. Weinthal, E., Vengosh, A., Marei, A., et al. (2005) The Water Crisis in the Gaza Strip: Prospects for Resolution. Groundwater, 43, 653-660.
http://dx.doi.org/10.1111/j.1745-6584.2005.00064.x - 26. Gharbia, S.S., Aish, A., Abushbak, T., et al. (2016) Evaluation of Wastewater Post-Treatment Options for Reuse Purposes in the Agricultural Sector under Rural Development Conditions. Journal of Water Process Engineering, 9, 111-122.
http://dx.doi.org/10.1016/j.jwpe.2015.12.003 - 27. Dentoni, M., Deidda, R., Paniconi, C., et al. (2015) A Simulation/Optimization Study to Assess Seawater Intrusion Management Strategies for the Gaza Strip Coastal Aquifer (Palestine). Hydrogeology Journal, 23, 249-264.
http://dx.doi.org/10.1007/s10040-014-1214-1 - 28. Yakirevich, A., Melloul, A., Sorek, S., et al. (1998) Simulation of Seawater Intrusion into the Khan Yunis Area of the Gaza Strip Coastal Aquifer. Hydrogeology Journal, 6, 549-559.
http://dx.doi.org/10.1007/s100400050175 - 29. Bruce, D., Friedman, G.M., Kaufman, A. and Yechieli, Y. (2001) Spatial Variations of Radiocarbon in the Coastal Aquifer of Israel; Indicators of Open and Closed Systems. Radiocarbon, 43, 783-791.
- 30. Goovaerts, P. (1996) Kriging vs. Stochastic Simulation for Risk Analysis in Soil Contamination. Proceedings of the 1st European Meeting on Geostatistics for Environmental Applications, Lisbon, 18-19 November 1996, 247-258.
- 31. Aidoo, E.N., Mueller, U., Goovaerts, P. and Hyndes, G.A. (2015) Evaluation of Geostatistical Estimators and Their Applicability to Characterize the Spatial Patterns of Recreational Fishing Catch Rates. Fisheries Research, 168, 20-32.
http://dx.doi.org/10.1016/j.fishres.2015.03.013 - 32. Lagadapati, Y., Shirvaikar, M. and Dong, X. (2015) Fast Semivariogram Computation Using FPGA Architectures. In: IS & T/SPIE Electronic Imaging, International Society for Optics and Photonics, USA, Vol. 9400, 05.
- 33. Olea, R., Pardo-Igúzquiza, E. and Dowd, P. (2015) Robust and Resistant Semivariogram Modelling Using a Generalized Bootstrap. Journal of the Southern African Institute of Mining and Metallurgy, 115, 37-44.
http://dx.doi.org/10.17159/2411-9717/2015/v115n1a4 - 34. Zimmerman, D.L. and Zimmerman, M.B. (1991) A Comparison of Spatial Semivariogram Estimators and Corresponding Ordinary Kriging Predictors. Technometrics, 33, 77-91.
http://dx.doi.org/10.1080/00401706.1991.10484771 - 35. Curran, P.J. (1988) The Semivariogram in Remote Sensing: An Introduction. Remote Sensing of Environment, 24, 493-507.
http://dx.doi.org/10.1016/0034-4257(88)90021-1 - 36. Webster, R. and Oliver, M.A. (2007) Geostatistics for Environmental Scientists. John Wiley & Sons, Chichester.
http://dx.doi.org/10.1002/9780470517277 - 37. Stigter, T., Ribeiro, L. and Dill, A.C. (2006) Application of a Groundwater Quality Index as an Assessment and Communication Tool in Agro-Environmental Policies—Two Portuguese Case Studies. Journal of Hydrology, 327, 578-591.
http://dx.doi.org/10.1016/j.jhydrol.2005.12.001 - 38. Vasanthavigar, M., Srinivasamoorthy, K., Chidambaram, S., et al. (2010) Application of Water Quality Index for Groundwater Quality Assessment: Thirumanimuttar Sub-Basin, Tamilnadu, India. Environmental Monitoring and Assessment, 171, 595-609.
http://dx.doi.org/10.1007/s10661-009-1302-1 - 39. Balan, I.N., Shivakumar, M. and Kumar, M. (2012) An Assessment of Groundwater Quality Using Water Quality Index in Chennai, Tamil Nadu, India. Chronicles of Young Scientists, 3, 146-150.
http://dx.doi.org/10.4103/2229-5186.98688 - 40. Jha, D.K., et al. (2015) Water Quality Assessment Using Water Quality Index and Geographical Information System Methods in the Coastal Waters of Andaman Sea, India. Marine Pollution Bulletin.
- 41. Al-Hadithi, M. (2012) Application of Water Quality Index to Assess Suitability of Groundwater Quality for Drinking Purposes in Ratmao-Pathri Rao Watershed, Haridwar District, India. American Journal of Scientific and Industrial Research, 10, 5251.
- 42. Ganeshkumar, B. and Jaideep, C. (2011) Groundwater Quality Assessment Using Water Quality Index (WQI) Approach—Case Study in a Coastal Region of Tamil Nadu, India. International Journal of Environmental Sciences and Research, 1, 50-55.
NOTES
*Corresponding author.






