Open Journal of Civil Engineering
Vol.05 No.02(2015), Article ID:57237,11 pages
10.4236/ojce.2015.52025
Influence of Mechanical Properties of Concrete and Soil on Solicitations of Mat Foundation
Oustasse Abdoulaye Sall1*, Makhaly Ba1, Mapathé Ndiaye1, Daouda Sangare2, Mathioro Fall1, Alassane Thiam1
1Département de Génie Civil, UFR SI-Université de Thiès, Thiès, Sénégal
2Département de Mathématiques, UFR SAT-Université Gaston Berger, Saint Louis, Sénégal
Email: *oustaz.sall@univ-thies.sn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 May 2015; accepted 13 June 2015; published 18 June 2015
ABSTRACT
This work studies the influence of mechanical and geometrical characteristics of the concrete and the soil on the stresses in a mat foundation. In this study, the soil-structure interaction is modeled by two parameters, the modulus of subgrade vertical reaction (k) and the modulus of subgrade horizontal reaction (2T). These two parameters are dependent on the geometrical and mechanical characteristics of the system. Results of this study show a sensitivity of solicitations to variations of geometrical and mechanical characteristics of the model. Although solicitations in the plate are sensitive to mechanical properties of concrete, these solicitations are strongly influenced by the mechanical and geometrical characteristics of the soil mass. However, it should be noted that the influence of Eb is denoted in the center of the plate whereas the Es feels almost in the same manner over the entire extent of the plate. This study also shows that for the same load cases, the values of the torsion moment and shear stress are not significant those of bending moments and normal stresses, respectively.
Keywords:
Plate, Soil-Structure Interaction, Mechanical Properties, Modeling, Solicitations

1. Introduction
Developments in the construction of civil engineering and especially disorders observed in the supporting structures push the practitioners to better take into account soil-structure interaction in the process of calculating the foundation structures. In addition to this, the structural and geotechnical calculations of foundations are generally conducted separately, that’s why it would be interesting to develop a computational approach that would take into account the geotechnical and structural considerations related to the problematic of the calculation of foundation. It is in this context that an accurate and complete characterization is needed for reliable calculation, hence the interest of this research. A foundation is responsible for transmitting loads from the superstructure to the soil. It provides an interface between the upper part of the structure and the soil. A mat foundation can be considered as a reinforced concrete slab over the whole of the structure whose study is mainly governed by the plate theory [1] . The behavior can be studied from the Lagrange equation with inclusion of the soil-structure interaction. The resolution of the behavioral model (theory of plate and soil-structure interaction) is possible with the use of methods of double Fourier series, numerical analysis (finite differences and finite elements) with boundary conditions defined [1] . This research studies the influence of mechanical properties of concrete and soil foundation on stresses generated by a uniformly distributed load applied on the plate.
2. Modeling the Raft on Soil Mass
2.1. Modeling of the Concrete Structure
A mat foundation is considered as a reinforced concrete slab resting on the soil mass. Usually, the thickness is small compared to other dimensions. It is in this context that the Kirchhoff model [2] is adopted in this study.
Mat foundations are structures in planar state constraints. They admit vertical displacements along the z axis and the behavioral model may be governed by the model of Kirchhoff for the plates [2] . The plate can be re- presented by the following Figure 1.
Considering the deflection (w) as known, the behavioral model of a plate supported on its periphery can be given by the following equation:
 (1)
(1)
where D is the flexural rigidity of the plate and is given by:
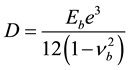 (2)
(2)
with:
Eb: elastic modulus of the material constituting the plate;
e: the thickness of the plate;
νb: Poisson’s ratio of the plate.
2.2. Modeling of Soil Mass
To model the subgrade, the Filonenko-Borodich biparametric model was selected. The model of Filonenko- Borodich [3] [4] provides continuity between the springs of the Winkler model by a thin elastic membrane under constant tension T (Figure 2) which connects the springs. Settlement (w) of the soil surface under pressure (q) is given by:
 (3)
(3)
Figure 1. Geometry of the plate and external forces.
Figure 2. Model of Filonenko-Borodich [5] .
with:
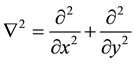 (4)
(4)
Both elastic constants of the model are the coefficient of reaction (k) and the tension (T). Figure 2 shows typical examples of settlement profiles in the case of a concentrated load (Figure 2(b)), a rigid foundation (Figure 2(c)) and a flexible foundation with a uniformly distributed load (Figure 2(d)).
The study of influencing factors in this model has been the subject of several scientific publications [6] .
2.2.1. Study of the Vertical Modulus of Subgrade Reaction (k)
Several authors have had to work on the modulus of reaction k, but all authors coming after Biot gave it a higher value than predicted by Biot [1] . In this research, the expression that was provided by Biot is used. Biot developed an empirical formula to express k [7] :
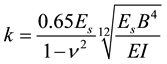 (5)
(5)
where:
Es is the modulus of subgrade;
νs is the Poisson's ratio of the subgrade;
B is the width of the foundation;
Eb is the Young modulus of the concrete foundation;
I is the moment of inertia of the cross section of the concrete.
2.2.2. Study of the Horizontal Modulus of Reaction (T)
The reaction shear modulus (T) has been proposed by Vlasov and given by the following relationship [8] :
 (6)
(6)
With:
Es: young’s modulus of the soil;
νs: soil Poisson ratio;
H: thickness of the soil layer (depth of the rigid substrate);
Ф(z): a function which describes the variation of the displacement w(x, y) along the z axis, such that:
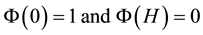
To a relatively deep layer of soil where the normal stress may vary with depth, it is possible to use, for the function Φ(z), two types of variation (linear or nonlinear). Selvadurai [5] proposes two possible entries of Ф(z) which are given by the following equations:
 (7)
(7)
 (8)
(8)
This work shows the displacements along the two variations of Ф(z). The linear variation gives after integration, the following shear parameter:
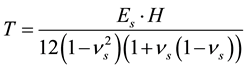 (9)
(9)
The hyperbolic variation leads to the following value of T:
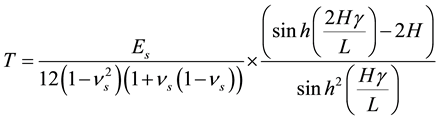 (10)
(10)
3. Presentation of the Calculation Model
To study the reinforced concrete structure, the Kirchhoff model was selected. For analysis of soil foundation, the Filonenko-Borodich model, which assimilates the soil to a spring assembly (elastic modulus k) infinitely close to each other and connected by an elastic membrane (2T voltage), was retained. The superposition of the two previous models leads to the behavior of the plate on the soil mass as shown by the Figure 3:
The theory of plate and taking into account the soil-structure interaction (biparametric model) lead to raft foundations behavioral law that may be governed by Equation (12) below:
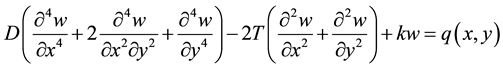 (12)
(12)
With the parameters D, k, T explained above.
4. Resolution of the Model
4.1. Analytical Calculation of Displacements
In this research, it is assumed a uniform distribution of forces applied to the foundation system. Therefore q(x, y) is a constant value “Q” because it can be assumed that at any point of the foundation, there is a uniform stress distribution. For analytical resolution of the system, the double Fourier series are used. So it is assumed that q(x, y) can be written in the following form:
Figure 3. Mapping of the problem [6] .
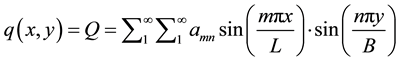 (13)
(13)
After analytical resolution, the expression of the deflection is given as follow:

At this value of deflection, it is added the displacements of the points of the interface under the effect of the dead weight of the slab before overload. This displacement is a function of the weight of slab and the value of the elastic modulus of the subgrade and estimated at 25,000 × e/k. From the analytical solution, it is able to demonstrate the influence of the parameters of the model of behavior on the displacement of the plate. A rectangular plate of 20 m × 20 m is considered, with thickness ranging from 20 cm to 80 cm. The plate rests on a soil with elastic modulus ranging between 4 MPa and 8 MPa and Poisson's ratio of between 0.2 and 0.45. The plate is subjected to uniform loading of 200 kN/m2. The influence of all these parameters is illustrated in the following (Figures 4-16).
Figure 4. Visualization of 2D displacements.
Figure 5. Visualization of 3D displacements.
Figure 6. Bending moment My visualization in 2D.
Figure 7. Bending moment My visualization in 3D.
Figure 8. Bending moment My for various values of Es.
Figure 9. Bending moment My for various values of Eb.
Figure 10. Bending moment My for various values of e.
Figure 11. Bending moment My for various values of νs.
Figure 12. Bending moment My for various values of νb.
Figure 13. Bending moment My for various values of H.
Figure 14. Normal stress σy on the faces.
Figure 15. Normal stress σy for various values of Eb.
Figure 16. Normal stress σy for various values of e.
4.2. Calculation of Solicitations
After determining the expression of w(x, y) at any point (x, y), the solicitations are given for the following expressions.
4.2.1. Determination of Moments and Shear Forces
Bending moments Mx My and torsion moment Mxy are given by:



Giving:



And shear forces are given by:




4.2.2. Calculation of Stresses
The stress state at the point m(x, y) is given by the following system of equations:






5. Presentation and Analysis of the Results
The study shows that even if the displacement is maximal at the center of the plate (Figure 4), the maximum values of the solicitations are not observed at the same point (center of the plate) as shown in Figure 6 and Figure 7. The maximum stress is located between the central third and supports of the plate. The study showed a sensitivity of stress compared to the variability of the model parameters (especially Es as shown in Figure 8). However, it is noted a strong sensitivity of the stresses to the mechanical and geometric variability of the characteristics of the concrete (Figure 9 and Figure 11), although the movements of the model are not too sensitive to mechanical parameters of concrete (Eb, νb) as shown by [1] [8] .
Figure 10 shows that the stresses are almost constants for low values of the thickness of the plate (for example e = 20 cm and e = 40 cm). The solicitations in the plate are very sensitive to the variability of the thickness. For a same load with fixed mechanical characteristics, by increasing the plate thickness, the stresses grow until the maximum value of the displacement is observed at the center of the plate (Figure 10 and Figure 16). Figure 13 shows the influence of the depth of the substratum on the internal forces and also shows that at high values of H, the solicitations are almost constant over the whole extent of the plate.
The stress distribution on the upper and lower faces of the plate (Figure 14). From this figure, it is noted a symmetrical distribution of these stresses compared with the average slip of the plate. The sensitivity of stress for various value of Eb is most felt in the center of the foundation (Figure 9 and Figure 15). The influence of soil Young’s modulus (Es) is almost felt in the same way over the entire plate (Figure 8). Figure 12 shows the variations of bending moment My for various values of Poisson’s ratio. Figure 16 shows a variation of the normal stresses with respect to the variability of the plate thickness. For high values of the thickness (e = 60 cm and 80 cm), the maximum value of stress is observed in the center of the foundation which is the case for low values of the thickness (e = 20 cm and 40 cm).
The study also shows that even for a distributed load, the values of torsion moment and shear stress were not significant. The results of this study combined with those of Sall [1] [8] shows that calculate a foundation with one design criterion (deformation criterion or strength criterion) only may lead to bad design. This study highlights the need to check both solicitations and displacements of the foundation (soil and plate).
6. Conclusion
Results from this research show that even if the displacement is maximal at the center plate, the maximum values of the stresses are not observed at the same point. The study shows a sensitivity of solicitations compared with a variability of geometrical and mechanical characteristics of the model. Although solicitations in the plate are sensitive to mechanical properties of concrete, they are strongly influenced by the mechanical and geometrical characteristics of the soil mass. However, it should be noted that the influence of Eb is denoted in the center of the plate whereas the influence of Es is almost the same over the entire extent of the plate. For low values of thickness, the interior efforts are almost constant on the full extent of the foundation. For high values of the depth of the rigid substrate, solicitations are almost constant over the whole of the plate. This study also shows that for the same load cases, the values of torsion moment and shear stress are not significant, compared respectively, with those of bending moments and normal stresses. This study also shows that calculations geotechnical and structural of the foundations should not be carried out separately. The results of this research should allow a good comprehension and a good taking into account of the soil-structure interaction in the calculation of foundations. In the future, it would be interesting to study the influence of the parameters of the model with more realistic laws of behavior.
References
- Sall, O.A (2015) Calcul analytique et modélisation de structure en plaque interaction sol-structure en vue du calcul des fondations superficielles en forme de radier. Thèse de Doctorat de l’Université de Thiès, Thiès, 125 p.
- Turhan, A. (1992) A Consistent Vlasov Model for Analysis on Plates on Elastic Foundation Using the Finite Element Method. The Graduate Faculty of Texas Tech University in Partial Fulfillment of the Requirements for the Degree of Doctor.
- Filonenko-Borodich, M.M. (1940) Some Approximate Theories of the Elastic Foundation. Uch. Zap. Mosk. Gos, Univ. Mekh. No. 46, 3-18.
- Filonenko-Borodich, M.M. (1945) A Very Simple Model of an Elastic Foundation Capable of Spreading the Load Sb Tr. Mosk. Elektro. Inst. Inzh. Trans., No. 53, Transzheldorizdat.
- Selvadurai, A.P.S. (1979) Elastic Analysis of Soil-Foundation Interaction. Developments in Geotechnical Engineering, 17, Elsevier Scientific Publishing Company.
- Sall, O.A, Fall, M., Berthaud, Y., Ba, M. and Ndiaye, M. (2013) Influence of the Elastic Modulus of the Soil and Concrete Foundation on the Displacements of a Mat Foundation. Open Journal of Civil Engineering, 3, 228-233. http://dx.doi.org/10.4236/ojce.2013.34027
- Biot, M.A (1937) Bending of an Infinite Beam on an Elastic Foundation. Journal of Applied Physics, 12, 155-164. http://dx.doi.org/10.1063/1.1712886
- Vlasov, V.Z. (1949) Structural Mechanics of Thin Walled Three Dimensional System. Stroizdat, Moscow.
NOTES
*Corresponding author.


















