Journal of Applied Mathematics and Physics
Vol.06 No.03(2018), Article ID:83347,14 pages
10.4236/jamp.2018.63051
On the Extension of the Three-Term Recurrence Relation to Probabilities Distributions without Moments
Habib Rebei, Anis Riahi
Department of Mathematics, College of Science, Qassim University, Al-Mulida, Saudi Arabia
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 18, 2017; Accepted: February 10, 2018; Published: March 28, 2018
ABSTRACT
In this paper, we extend the three-term recurrence relation for orthogonal polynomials associated with a probability distribution having a finite moment of all orders to a class of orthogonal functions associated with an infinitely divisible probability distribution 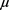 having a finite moments of order less or equal to four. An explicit expression of these functions will be given in term of the Lévy-Khintchine function of the measure
having a finite moments of order less or equal to four. An explicit expression of these functions will be given in term of the Lévy-Khintchine function of the measure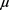 .
.
Keywords:
Three-Term Recurrence Relation, Quantum Decomposition of Random Variables Without Moments, Lévy-Khintchine Function

1. Introduction
It has been known from [1] and [2] that for every probability distribution 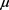 with finite moments of all orders, there exits a family of monic orthogonal polynomials
with finite moments of all orders, there exits a family of monic orthogonal polynomials 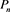 and a paire of sequences
and a paire of sequences 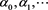 and
and 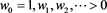 satisfying the three-term recurrence relation (or the tri-diagonal Jacobi relation)
satisfying the three-term recurrence relation (or the tri-diagonal Jacobi relation)
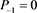 (1)
(1)
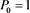 (2)
(2)
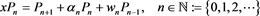 (3)
(3)
The sequences (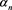 ) and (
) and (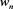 ) are called the Szego-Jacobi parameters of
) are called the Szego-Jacobi parameters of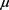 .
.
The starting point of the quantum probabilistic approach to the theory of orthogonal polynomials (OP) is an operator interpretation of the tri-diagonal Jacobi relation (3) in terms of Creation, Annihilation and Preservation (CAP) operators. This allows to associate, in a canonical way, to any random variable with all moments commutation relations that generalize the Heisenberg commutation relations (corresponding to the Gauss-Poisson class). From the mathematical point of view, this approach has led to some new results in the theory of OP.
In order to give this operator interpretation, we shall recall the notion of the interacting Fock probability space associated with the measure 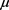 (See [3] for more details).
(See [3] for more details).
Consider an infinite-dimensional separable Hilbert space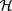 , in which a complete orthonormal basis
, in which a complete orthonormal basis 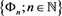 is chosen. Let
is chosen. Let 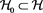 denote the dense subspace spanned by the complete orthonormal basis
denote the dense subspace spanned by the complete orthonormal basis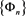 .
.
Given the sequence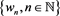 , we associate linear operators
, we associate linear operators 
Its known that 



The quadruple 



is called the number operator. More generally, with the sequence

Let 









where
This means that the field operator 






This shows that any classical random variable has a built in non commutative structure which is intrinsic and canonical, and not artificially put by hands, that is a sum of three non commuting random variables.
This result motivated the apparition of a series of papers [4] - [9] dealing in the same context and provided many applications in the theory of quantum probability. In the paper [4] , a similar result was obtained but for the family of random variables having an infinitely divisible distribution (I.D-distribution in the following) and having only the moment of the second order. Here, similarity means that the quantum decomposition can be obtained also for this family of random variables.
Based on the notion of the positive definite kernel and using the Lévy-Khintchine function established for the I.D-distributions, the paper [4] constructed a natural isomorphism U from the Fock space 





where 

In this approach, the construction was not based on the orthogonal polynomials sequence associated with


This paper is organized as follows:
In Section 2, we recall some known facts about the bosonic Fock space and the quantum decomposition of classical random variables without moments, having I.D-distributions, obtained in [12] [4] and [5] . In Section 3, we compute the action of the generalized field operator 



2. Preliminaries
2.1. The Bosonic Fock Space
Let 





where 
Let

be the orthogonal projection.
We define
where
Let us denote
Then


The bosonic creation and annihilation operators are defined, on the total set
as follows:
For

and

and
where 


2.2. The Quantum Decomposition of Classical Random Variables with I.D-Distributions
In this section, we recall briefly, what has been obtained in the paper [4] around quantum decomposition of random variables with I.D-distributions and having a finite second order moment.
Let us consider a random variable X with I.D-probability distribution 


where 

such that 




Since the second order moment of 


We suppose also that the gaussian part of 

The family 


is total in
Then by applying the Araki-Woods-Parthasarathy-Schmidt isomorphism in [12] for the infinitely divisible positive definite kernel
we have proved the following theorem (See [4] for more details and descriptions).
Theorem 2.1. The unique linear operator U given on the exponential vectors 

is an unitary isomorphism from the Fock space 

Definition 1. Let q be the multiplication (position) operator in
Define the operator Q on 
where U is the isomorphism defined by (12). Since 

The operator Q is called the generalized field operator.
It follows from condition (10) that the total set 
Theorem 2.2. Let 
Then the generalized field operator Q takes the form

where


3. The Generalized Field Operator
3.1. Notations
We denote by 




For 

The support of such element 
When 


In particular if 


then
From [15] , we recall the following identity which is the analogue of the multinomial Newton formula

which take place whenever the series 
If 

is an orthonormal basis of the Hilbert space

Let 



and

Note that if




Finally, we recall that


3.2. Computation of the Action of the Generalized Field Operator on the Basis (Fn)n
In the remain, we take 



Since the set 



Lemma 3.1. If the 4th-moment of 


Proof. We have
Then



We have
where we have used the condition (10).
,
Proposition 3.1. Let 

where 



where
Remark 1. Note that the relation (22) still true in the case when 

Proof. From (5), we have
This prove (21).
From (5), we have

Here, we have two cases:
If

If


But in view of (17), we have 
Now, it remains to justify (23). From (7), we get

Since
Using the fact that 

But we have for

Then (27) becomes
This ends the proof. ,
Corollary 3.1.1 The action of the generalized field operator Q on the basis 

(29)
Proof. A straightforward computations. ,
4. Orthogonal Functions and Generalization of the Three-Term Recurrence Relation
In this section, we give the action of the multiplication operator q on the functions
Then we deduce the generalization of the three-term recurrence relation in term of the orthogonal functions
Since U is unitary from 





Theorem 4.1 Let 


Then for all

Remark 2. Since U is unitary and the basis 



Now comparing the relation (30) with (3), the only difference is the apparition of a corrective expression 



Proof. From relation (29), we deduce that
Proposition 4.2. We assume that 




where,
Proof. Since 


where the series converge in
where
This implies that
From the definition of U, we get
which is the decomposition of 

On the other hand, we have
This implies that
or equivalently
where 



,
which is equivalent to
5. Conclusion
The infinite-divisibility of the distribution 


Acknowledgements
The authors gratefully acknowledge Qassim University, represented by the Deanship of Scientific Research, on the material support for this research under the number 3378 during the academic year 1436 AH/2015 AD.
Cite this paper
Rebei, H. and Riahi, A. (2018) On the Extension of the Three-Term Recurrence Relation to Probabilities Distributions without Moments. Journal of Applied Mathematics and Physics, 6, 588-601. https://doi.org/10.4236/jamp.2018.63051
References
- 1. Hora, A. and Obata, N. (2007) Quantum Probability and Spectral Analysis of Graphs, Theoretical and Mathematical Physics. Springer, Berlin, Heidelberg.
- 2. Asai, N., Kubo, I. and Kuo, H.H. (2003) Generating Functions of Orthogonal Polynomials and Szego-Jacobi Parameters. Probability and Mathematical Statistics, 23, 273-291.
- 3. Accardi, L. and Bozejko, M. (1998) Interacting Fock Space and Gaussianization of Probability Measures. Infinite Dimensional Analysis, Quantum Probability and Related Topics, 1, 663-670. https://doi.org/10.1142/S0219025798000363
- 4. Accardi, L., Rebei, H. and Riahi, A. (2013) The Quantum Decomposition of Infinitely Divisible Random Variables. Infinite Dimensional Analysis, Quantum Probability and Related Topics, 16, 1350012.
- 5. Accardi, L., Rebei, H. and Riahi, A. (2014) The Quantum Decomposition Associated with the Lévy White Noise Processes without Moments. Probability and Mathematical Statistics, 34, 337-362.
- 6. Accardi, L., Ouerdiane, H. and Rebei, H. (2010) On the Quadratic Heisenberg Group. Infinite Dimensional Analysis, Quantum Probability and Related Topics, 13, 551-587. https://doi.org/10.1142/S0219025710004231
- 7. Rebei, H. (2015) The Generalized Heisenberg Group Arising from Weyl Relations, Quantum Studies. Mathematics and Foundations, 2, 323-350.
- 8. Rebei, H. (2016) On the One Mode Quadratic Weyl Operators. Journal of Mathematical Analysis and Applications, 439, 135-153. https://doi.org/10.1016/j.jmaa.2016.02.040
- 9. Rebei, H., Al-Mohaimeed, B. and Riahi, A. (2015) Classical Versions of Quantum Stochastic Processes Associated with the Adapted Oscillator Algebra. International Journal of Innovation in Science and Mathematics, 3, 245-253.
- 10. Accardi, L., Ouerdiane, H. and Rebei, H. (2012) Lévy Processes through Time Schift on Oscillator Weyl Algebra. Communications on Stochastic Analysis, 6, 125-155.
- 11. Accardi, L., Ouerdiane, H. and Rebei, H. (2012) Renormalized Square of White Noise Quantum Time Shift. Communications on Stochastic Analysis, 6, 177-191.
- 12. Accardi, L., Boukas, A. and Misiewicz, J. (2011) Existence of the Fock Representation for Current Algebras of the Galilei Algebra. QP-PQ: Quantum Probability and Related Topics, 27, 1-33.
- 13. Sato, K.-I. (1999) Lévy Processes and Infinitely Divisible Distributions. Cambridge Stud. Adv. Math., Cambridge Univ. Press, Cambridge.
- 14. Reed, M. and Simon, B. (1980) Functional Analysis, Methods of Modern Mathematical Physics. Vol. 1. Academic Press, INC., London.
- 15. Stochel, J.B. (1992) Subnormality of Generalized Cration and Annihilation Operators on Bargmann’s Space of Infinite Order. Integral Equations and Operator Theory, 15, 1011-1032.































































