ABSTRACT

This is a survey on our recent works on bi-harmonic maps on CR-manifolds and foliated Riemannian manifolds, and also a research paper on bi-harmonic maps principal G-bundles. We will show, (1) for a complete strictly pseudoconvex CR manifold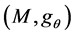, every pseudo bi-harmonic isometric immersion 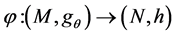into a Riemannian manifold of non-positive curvature, with finite energy and finite bi- energy, must be pseudo harmonic; (2) for a smooth foliated map of a complete, possibly non-compact, foliated Riemannian manifold into another foliated Riemannian manifold, of which transversal sectional curvature is non-positive, we will show that if it is transversally bi-harmonic map with the finite energy and finite bienergy, then it is transversally harmonic; (3) we will claim that the similar result holds for principal G-bundle over a Riemannian manifold of negative Ricci curvature.

Keywords:

Foliation, Divergence Theorem, Transversally Harmonic, Transversally Biharmonic

1. Introduction

The theory of harmonic maps has been extensively developed and applied in many problems in topology and differential geometry (cf. [1] [2] [3] , etc.). Eells and Lemaire raised ( [3] ) a problem to study 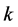-harmonic maps and G. Y. Jiang calculated [4] the first variational and second formulas of the bienergy.

On the other hand, B.Y. Chen proposed [5] the famous conjecture in the study of sub-manifolds in the Euclidean space. B. Y. Chen’s conjecture and the generalized B. Y. Chen’s conjecture are as follows:

The B. Y. Chen’s conjecture: Every biharmonic isometric immersion into the Eucli- dean space 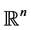must be harmonic (minimal).

The generalized B. Y. Chen’s conjecture: Every biharmonic isometric immersion of a Riemannian manifold 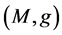into a Riemannian manifold 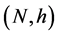of non-positive curvature must be harmonic (minimal).

The B. Y. Chen’s conjecture is still open, but the generalized B. Y. Chen’s conjecture was solved negatively by Ye-Lin Ou and Liang Tang [6] , due to several authors have contributed to give partial answers to solve these problems (cf. [7] - [17] ).

For the first and second variational formula of the bienergy, see [4] .

Then, the CR analogue for harmonic maps and biharmonic maps has been raised as follows.

The CR analogue of the generalized Chen’s conjecture: Let 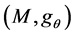be a complete strictly pseudoconvex CR manifold, and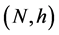, a Riemannian manifold of non-positive curvature. Then, every pseudo biharmonic isometric immersion must be pseudo harmonic.

For the works on CR analogue of biharmonic maps, see [18] [19] [20] . We will show (cf. [20] ):

Theorem 1.1. (cf. Theorem 2.1) Let 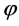be a pseudo biharmonic map of a strictly pseudoconvex complete CR manifold 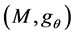into another Riemannian manifold of non positive curvature.

If has finite pseudo bienergy 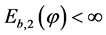and finite pseudo energy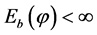, then it is pseudo harmonic, i.e.,.

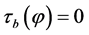Next, let us consider the analogue of harmonic maps and biharmonic maps for foliations are also given as follows. Transversally biharmonic maps between two foliated Riemannian manifolds were introduced by Chiang and Wolak (cf. [21] ) and see also [22] [23] [24] [25] [26] . They are generalizations of transversally harmonic maps introduced by Konderak and Wolak (cf. [27] [28] ).

Among smooth foliated maps between two Riemannian foliated manifolds, one can define the transversal energy and derive the Euler-Lagrange equation, and transversally harmonic map as its critical points which are by definition the transversal tension field vanishes,. The transverse bienergy can be also defined as

whose Euler-Lagrange equation is that the transversal biten-

sion field vanishes and the transversally biharmonic maps which are, by definition, vanishing of the transverse bitension field.

Recently, S.D. Jung studied extensively the transversally harmonic maps and the transversally biharmonic maps on compact Riemannian foliated manifolds (cf. [29] [30] [31] [32] ).

Then, we will study transversally biharmonic maps of a complete (possibly non- compact) Riemannian foliated manifold into another Riemannian foliated manifold of which transversal sectional curvature is non-positive. Then, we will show (cf. [33] ) that:

Theorem 1.2. (cf. Theorem 2.6) Let and be two Riemannian foliated manifolds, and assume that the transversal sectional curvature of is non-positive. Let be a smooth foliated map which is an isometric immersion of into. If is transversally biharmonic with the finite transversal energy and finite transversal bienergy, then it is transversally harmonic.

Finally, in Section 5, instead of isometric immersions, we will consider a principal G-bundle, and show a new result whose details will be appeared in [34] .

Theorem 1.3. (cf. Theorem 5.1) Let be a principal G-bundle over a Riemannian manifold whose Ricci tensor is negative definite. Then, if is biharmonic, then it is harmonic.

2. Preliminaries

2.1. First and Second Variational Formulas for the Energy

First, let us recall the theory of harmonic maps. For a smooth map of a Riemannian manifold into another Riemannian manifold, the energy functional is defined by

(2.1)

whose first variational formula is:

(2.2)

Here, V is a variational vector field is given by, ,

and the tension field is given by

(2.3)

(2.4)

where and are Levi-Civita connections of and, respectively. Then, is harmonic if.

The second variation formula of the energy functional for a harmonic map is:

(2.5)

where

(2.6)

(2.7)

where is a locally defined frame field on. The -energy functional due to J. Eells and L. Lemaire ( [1] [2] [3] ) is

(2.8)

which turn out that

(2.9)

Furthermore, the first variation formula for is (cf. [4] ):

(2.10)

(2.11)

Then, one can define that is biharmonic (cf. [4] ) if.

2.2. The CR Analogue of the Generalized Chen’s Conjecture

In this part, we first raise the CR analogue of the generalized Chen’s conjecture, and settle it for pseudo biharmonic maps with finite pseudo energy and finite pseudo bienergy.

Let us recall a strictly pseudoconvex CR manifold (possibly non compact) of -dimension, and the Webster Riemannian metric given by

for. Recall the material on the Levi-Civita connection of. Due to Lemma 1.3, Page 38 in [35] , it holds that,

(2.12)

where is the Tanaka-Webster connection, , and, , and is the torsion tensor of. And also, ,

for all vector fields X, Y on M. Here, J is the

complex structure on and is extended as an endomorphism on by.

Then, we have

(2.13)

(2.14)

where is a locally defined orthonormal frame field on with respect to g_θ, and T is the characteristic vector field of. For (3.6), it follows from that, and since. For (3.7), notice that the Tanaka-Webster connection satisfies, and also and JT = 0, so that which imply (3.7).

Let us consider the generalized B.-Y. Chen’s conjecture for pseudo biharmonic maps which is CR analogue of the usual generalized Chen’s conjecture for biharmonic maps:

The CR analogue of the generalized B.-Y. Chen’s conjecture for pseudo bihar- monic maps:

Let be a complete strictly pseudoconvex CR manifold, and assume that is a Riemannian manifold of non-positive curvature.

Then, every pseudo biharmonic isometric immersion must be pseudo harmonic.

Then, we will show:

Theorem 2.1. Assume that φ is a pseudo biharmonic map of a strictly pseudoconvex complete CR manifold into another Riemannian manifold of non positive curvature.

If φ has finite pseudo bienergy and finite pseudo energy, then it is pseudo harmonic, i.e.,.

2.3. The Green’s Formula on a Foliated Riemannian Manifold

Then, we prepare the materials for the first and second variational formulas for the transversal energy of a smooth foliated map between two foliated Riemannian manifolds following [31] [32] [36] . Let be an -dimensional foliated Riemannian manifold with foliation of codimension q and a bundle-like Riemannian metric g with respect to (cf. [37] [38] ). Let TM be the tangent bundle of M, L, the tangent bundle of, and Q = TML, the corresponding normal bundle of. We denote the induced Riemannian metric on the normal bundle Q, and, the transversal Levi-Civita connection on Q, , the transversal curvature tensor, and, the transversal sectional curvature, respectively. Notice that the bundle projection is an element of the space of Q-valued 1-forms on M. Then, one can obtain the Q-valued bilinear form on M, called the second fundamental form of, defined by

The trace of, called the tension field of is defined by

where spanns on a neighborhood U on M. The Green’s theorem, due to Yorozu and Tanemura [36] , of a foliated Riemannian manifold says that

(2.15)

where denotes the transversal divergence of with respect to given by. Here spanns where

is the orthogonal complement bundle of L with a natural identification.

2.4. The Variational Formulas for Foliations

Let, and be two compact foliated Riemannian manifolds. The transversal energy among the totality of smooth foliated maps from into by

(2.16)

Here, a smooth map is a foliated map is, by definition, for every leaf L of, there exists a leaf of satisfying. Then, can be regarded as a section of where is a subspace of the cotangent bundle T*M. Here, π, are the projections of and. Notice that our definition of the transversal energy is a slightly different from the one of Jung’s definition (cf. [32] , p. 5).

The first variational formula is given (cf. [?]), for every smooth foliated variation

with and in which being a section,

(2.17)

Here, is the transversal tension field defined by

(2.18)

where is the induced connection in from the Levi-Civita connection of, and is a locally defined orthonormal frame field on Q.

Definition 2.2. A smooth foliated map is said to be transversally harmonic if.

Then, for a transversally harmonic map, the second variation formula of the transversal energy is given as follows (cf. [?], p. 7) : let be any two parameter smooth foliated variation of

with, and,

(2.19)

where is a second order semi-elliptic differential operator acting on the space of sections of which is of the form:

(2.20)

for. Here, is the Levi-Civita connection of, and recall also that:

(2.21)

(2.22)

Definition 2.3. The transversal bitension field of a smooth foliated map is defined by

(2.23)

Definition 2.4. The transversal bienergy E₂ of a smooth foliated map is defined by

(2.24)

Remark that this definition of the transversal bienergy is also slightly different from the one of Jung (cf. Jung [32] , p. 13, Definition 6.1). On the first variation formula of the transversal bienergy is given as follows. For a smooth foliated map φ and a smooth foliated variation of, it holds (cf. [32] , p. 13) that

(2.25)

Definition 2.5. A smooth foliated map is said to be transversally biharmonic if.

Then, one can ask the following generalized B.Y. Chen’s conjecture:

The generalized Chen’s conjecture:

Let be a transversally biharmonic map from a foliated Riemannian manifold into another foliated Riemannian manifold whose transversal sectional curvature is non-positive. Then, must be transversally harmonic.

Then, we can state our main theorem which gives an affirmative partial answer to the above generalized Chen’s conjecture under the additional assumption that has both the finite transversal energy and the finite transversal bienergy:

Theorem 2.6. Let a smooth foliated map which is an isometric immersion of into. Assume that is complete (possibly non-compact), and the transversal sectional curvature of is non-positive.

If φ is transversally biharmonic having both the finite transversal energy and the finite transversal bienergy, then it is transversally harmonic.

Remark that in the case that is compact, Theorem 2.5 is true due to Jung’s work (cf. [32] Theorem 6.4, p. 14).

3. Proof of Theorem 2.1

The proof of Theorem 2.1 is divided into several steps which will appear in [20] .

(The first step) For an arbitrarily fixed point, let where is a distance function on, and let us take a cut off function on, i.e.,

(3.1)

where r is the distance function from, and is the Levi-Civita connection of, respectively. Assume that is a pseudo biharmonic map, i.e.,

(3.2)

(The second step) Then, we have

(3.3)

In (3.3), notice that is the sectional curvature of corresponding to the vectors and. Since has the non-positive sectional curvature, (3.3) is non-positive.

On the other hand, for the left hand side of (3.3), it holds that

(3.4)

Here, let us recall, for,

where is a locally defined orthonormal frame field of and is defined by

for and. Here, is the -component of corresponding to the decomposition of , and is the induced connection of from the Levi-Civita con- nection of.

Since

(3.5)

the right hand side of (3.4) is equal to

(3.6)

Therefore, together with (3.3), we have

(3.7)

where we define by

Then, it holds that for every which implies that

Therefore, we have that

The right hand side of (3.7)

(3.8)

foe every. By taking, we obtain

(3.9)

Therefore, we obtain, due to the properties that on, and

,

(3.10)

(The third step) By our assumption that and

is complete, if we let, then goes to M, and the right hand side of (3.10) goes to zero. We have

(3.11)

This implies that

(3.12)

(The fourth step) Let us take a 1 form on M defined by

Then, we have

(3.13)

where we put,

and

(3.14)

Furthermore, let us define a function on M by

(3.15)

where is the Tanaka-Webster connection. Notice that

(3.16)

where is the natural projection. We used the facts that, and ( [35] , p.37). Here, recall again is the Levi-Civita connection of, and is the Tanaka-Webster connection. Then, we have, for (3.16),

(3.17)

We used (3.12) to derive the last second equality of (3.17). Then, due to (3.17), we have for,

(3.18)

In the last equality, we used Gaffney’s theorem ( [16] , p. 271, [?]).

Therefore, we obtain, i.e., is pseudo harmonic.

We obtain Theorem 2.1.

4. Proof of Main Theorem 2.6

In this section, we give a proof of Theorem 2.6 which will appear in [34] , by a similar way to the case of foliations as Theorem 2.1.

(The first step) First, let us take a cut off function from a fixed point on, i.e.,

where, is a distance function from on, is the Levi-Civita connection of, respectively.

Assume that is a transversally biharmonic map of into, i.e.,

(4.1)

where recall is the induced connection on.

(The second step) Then, by (4.1), we obtain that

(4.2)

where the sectional curvature of corresponding to the plane spanned by and is non-positive.

(The third step) On the other hand, the left hand side of (4.2) is equal to

(4.3)

since

Together (4.2) and (4.3), we obtain

(4.4)

Because, putting, , we have

which is

(4.5)

If we put in (4.5), then we obtain

(4.6)

By (4.6), we have the second inequality of (4.4).

(The fourth step) Noticing that η = 1 on and in the inequality

(3.4), we obtain

(4.7)

Letting, the right hand side of (4.7) converges to zero since

. But due to (4.7), the left hand side of (4.7) must converge to since tends to M because is complete.

Therefore, we obtain that

which implies that

(4.8)

(The fifth step) Let us define a 1-form on M by

(4.9)

and a canonical dual vector field on M by. Then, its divergence written as

,

can be given as follows. Here, and are locally defined orthonormal frame fields on leaves L of and Q, respectively, (, ,).

Then, we can calculate as follows:

(4.10)

since in the last equality of (4.10). Integrating the both hands of (4.10) over M, we have

(4.11)

because of. Notice that both hands in (4.11) are well defined because of and.

Since is the second fundamental form of each leaf L in and

(4.12)

the right hand side of (4.11) coincides with

(4.13)

(4.11) is equivalent to that

(4.14)

If is an isometric immersion, then it holds that, which implies that both the left hand side and the second term of the right hand side of (4.14) vanish, that is,. Therefore.

We obtain Theorem 2.6.

5. Principal G-Bundles

In this section, we show the following theorem which is quite new and the more detail [34] will appear elsewhere.

Theorem 5.1 Let be a principal G-bundle over a Riemannian manifold whose Ricci tensor is negative definite. Then, if is biharmonic, then it is harmonic.

Let us consider a principal G-bundle whose the total space P is compact. Assume that the projection is biharmonic, which is by definition, , where is the tension field of which is defined by

(5.1)

the Jacobi operator J is defined by

(5.2)

is the rough Laplacian defined by

(5.3)

and

(5.4)

where is a locally defined orthonormal frame field on.

The tangent space is canonically decomposed into the orthogonal direct sum of the vertical subspace and the horizontal subspace:. Then, we have

where, respectively. Then, we obtain

Therefore, we obtain

(5.5)

where we denote by , the sectional curvature of through two plane of given by, and is the Ricci curvature of along. The left hand side of (5.5) is non-negative, and then, the both hand sides of (5.5) must vanish if the Ricci curvature of is non-positive. Therefore, we obtain

(5.6)

Let us consider a 1-form on M defined by

(5.7)

Then, for every, we have

(5.8)

which implies that is parallel 1-form on. Since we assume that the Ricci tensor of is negative definite, must vanish (so called Bochner’s theorem, cf. [40] , p. 55). Therefore, , i.e., the projection of the principal G-bundle is harmonic. We obtain Theorem 5.1.

Acknowledgements

None.

Funding

Supported by the Grant-in-Aid for the Scientific Research, (C) No. 25400154, Japan Society for the Promotion of Science.

Cite this paper

Ohno, S., Sakai, T. and Urakawa, H. (2016) Harmonic Maps and Bi-Harmonic Maps on CR-Manifolds and Foliated Riemannian Manifolds. Journal of Applied Mathematics and Physics, 4, 2272-2289. http://dx.doi.org/10.4236/jamp.2016.412219

References