Received 2 March 2016; accepted 24 April 2016; published 28 April 2016

ABSTRACT

In this paper we introduce the notion of the Henstock-Stieltjes (HS) integrals of interval-valued functions and fuzzy-number-valued functions and discuss some of their properties.

Keywords:

Fuzzy Numbers, Henstock-Stieltjes (HS) Integrals of Interval-Valued Functions, Henstock-Stieltjes (HS) Integrals of Fuzzy-Number-Valued Functions

1. Introduction

As it is well known, the Henstock (H) integral for a real function was first defined by Henstock [1] in 1963. The Henstock (H) integral is a lot powerful and easier than the Lebesgue, Wiener and Richard Phillips Feynman integrals. Furthermore, it is also equal to the Denjoy and the Perron integrals [1] [2] . In 2000, Congxin Wu and Zengtai Gong [3] introduced the notion of the Henstock (H) integrals of interval-valued functions and fuzzy- number-valued functions and obtained a number of their properties. In 2016, Yoon [4] introduced the interval- valued Henstock-Stieltjes integral on time scales and investigated some properties of these integrals. In 1998, Lim et al. [5] introduced the notion of the Henstock-Stieltjes (HS) integral of real-valued function which was a generalization of the Henstock (H) integral and obtained its properties.

In this paper, we tend to introduce the notion of the Henstock-Stieltjes (HS) integrals of interval-valued functions and fuzzy-number-valued functions and discuss some of their properties.

The paper is organized as follows. In Section two, we tend to give the preliminary terminology used in the present paper. Section three is dedicated to discussing the Henstock-Stieltjes (HS) integral of interval-valued functions. In Section four, we tend to introduce the Henstock-Stieltjes (HS) integral of fuzzy-number-valued functions. The last section provides conclusions.

2. Preliminaries

Definition 2.1 [1] [2] Let 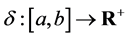be a positive real-valued function. 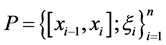is called a d- fine division, if the subsequent conditions are satisfied:

1),

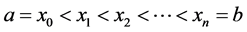2)

For brevity, we write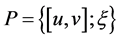, wherever 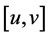denotes a typical interval in P and 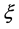is that the associated point of.

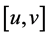Definition 2.2 [1] [2] A real-valued function 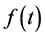is called Henstock (H) integrable to A on 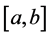if for each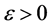, there exists a function 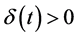such that for any d-fine division 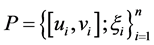of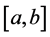, we have

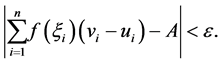(1)

where the sum is understood to be over P, we write, and.

Definition 2.3 [5] Let be an increasing function. A real-valued function is Henstock-Stieltjes (HS) integrable to with respect to on if for each, there exists a function, such that for any d-fine division we have

(2)

We write, and.

Lemma 2.1 [5] Let be an increasing function and let f, g are Henstock-Stieltjes (HS) integrable with respect to on. If and almost everywhere on, then

(3)

3. The Henstock-Stieltjes (HS) Integrals of Interval-Valued Functions

Definition 3.1 [3] Let.

For, we define if and only if and, if and only if and, and, wherever and

Define as the distance between intervals A and B.

Definition 3.2 [3] Let be an interval-valued function., for each there exists a such that for any d-fine division we have

(4)

then is called the Henstock (H) integrable over and write. Also, we write.

Definition 3.3 Let be an increasing function. An interval-valued function is Henstock-Stieltjes (HS) integrable to with respect to on, if for each there exists a such that for any d- fine division, we have

(5)

We write and

Theorem 3.1 Let be an increasing function. If, then there exists a unique integral value.

Proof Let the integral value is not unique and let and. If is given. Then there exists a such that for any d- fine division, we have

(6)

(7)

Since for all there exists a as above then

Theorem 3.2 Let be an increasing function. Then an interval-valued function iff and

(8)

Proof If, by Definition 3.3 there exists a unique interval number with the

property, for any there exists a such that for any d- fine division, we have

(9)

that is

(10)

Since for we have

(11)

(12)

Therefore, by Definition 2.3 we can obtain and

(13)

(14)

Conversely, let, then there exists a unique with the property, given

there exists a such that for any -fine division, we have

(15)

It is similar to find such that for any -fine division, we have

(16)

If, then We define and then for any d- fine division, we have

(17)

Hence is Henstock-Stieltjes (HS) integrable with respect to on.

Theorem 3.3 If and Then

i) and

(18)

ii) Let almost everywhere on. Then

(19)

Proof i) If, then by Theorem 3.2. Hence

1) If and then

2) If and then

3) If and (or and), then

Similarly, for four cases above we have

(20)

Hence by Theorem 3.2 and

(21)

ii) The proof is similar to Theorem 2.8 in [5] .

Theorem 3.4 Let and let Then and

(22)

Proof If and, then by Theorem 3.2 and . Hence and

Similarly, Hence by Theorem 3.2 and

(23)

Theorem 3.5 Let be an increasing function such that If nearly everywhere on and, then

(24)

Proof Let nearly everywhere on and Then and, nearly everywhere on. By Lemma 2.1

and Hence

(25)

by Theorem 3.2.

Theorem 3.6 Let and is Lebesgue-Stieltjes (LS) integrable on. Then

(26)

Proof By definition of distance,

(27)

4. The Henstock-Stieltjes (HS) Integral of Fuzzy-Number-Valued Functions

Definition 4.1 [6] - [8] If is a fuzzy subset on. If for any and wherever then is called a fuzzy number. If satisfy the following conditions: 1) convex, 2) normal, 3) upper semi-continuous, 4) has the compact support, then is called a compact fuzzy number.

Let denote the set of all fuzzy numbers and denote the set of all compact fuzzy numbers.

Definition 4.2 [6] Let, we define if and only if for all if and only if for any if and only if for any

For is called the distance between and

Lemma 4.1 [9] If a mapping satisfies when then

(28)

and

(29)

where

Definition 4.3 [3] Let and let the interval-valued function is Henstock (H) integrable on for any then is called Henstock (H) integrable on and the integral value is defined by

We write

Definition 4.4 Let be an increasing function and let. If the interval-valued function is Henstock-Stieltjes (HS) integrable with respect to on for any then is called Henstock-Stieltjes (HS) integrable with respect to on and the integral value is defined by

We write

Theorem 4.1 then and

(30)

where

Proof Let be defined by

Since and are increasing and decreasing on respectively, therefore, when we have on. From Theorem 3.5 we have

(31)

From Theorem 3.2 and Lemma 4.1 we have

(32)

and wherever

Using Theorem 4.1 and the properties of integral, we are able to get the properties of integral, for example, 1) the linear, 2) monotone, 3) interval additive properties of integral.

5. Conclusion

In this paper, we proposed the definition of the Henstock-Stieltjes (HS) integrals of interval-valued functions and fuzzy-number-valued functions and investigated some properties of those integrals.

Cite this paper

Muawya Elsheikh Hamid,Alshaikh Hamed Elmuiz, (2016) On Henstock-Stieltjes Integrals of Interval-Valued Functions and Fuzzy-Number-Valued Functions. Journal of Applied Mathematics and Physics,04,779-786. doi: 10.4236/jamp.2016.44088

References

NOTES

^*Corresponding author.