Received 21 January 2016; accepted 22 February 2016; published 25 February 2016

ABSTRACT

This numerical study investigates the steady state unimolecular thermal decomposition of a che- mical dissolved in water inside a parallel-plate reactor containing four heated circular rods using a penalty Galerkin finite element approach. The reactant fluid enters from the left inlet and exits from the right outlet of the reactor. All solid walls of the reactor are assumed to be thermodynamically isolated. The aim of the investigation is to illustrate the effects of the energy expelled during the reaction, temperature of the heated rods and fluid inlet velocity on the thermal field and concentration of the heat sensitive chemical. The simulation is conducted for different values of inlet velocity and rods temperature taking into consideration and neglecting the reaction energy. From the results, it is concluded that the thermal field and decomposition process of the chemical are significantly influenced by fluid velocity, rods temperature and the reaction type.

Keywords:

Finite Elements, Heat and Mass Transfer, Chemically Reacting Flows, Navier-Stokes Equation

1. Introduction

A unimolecular reaction is in principle the simplest kind of elementary reaction since it involves the decomposition or isomerization of a single reactant. The next example will illustrate the mechanism of the unimolecular decomposition. The following elementary reaction,

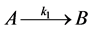(1)

is unimolecular because there is only one molecule reacting, that is, molecule “A” is reacting.

This unimolecular reaction step implies the following rate law,

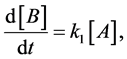(2)

or, equivalently,

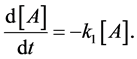(3)

In words, these elementary reactions state that the molecule, A, spontaneously transforms into B at some reaction rate k₁. The algebraic sign in front of k₁ tells whether you are gaining product or losing reactant depending on whether the concentration in the derivative is increasing or decreasing. For example, in Equation (2), “B” is increasing, and in Equation (3), “A” is decreasing.

The study of a unimolecular reaction is of paramount importance in chemical engineering. Recently, various experimental and numerical investigations have been done to examine characteristics and mechanisms of the unimolecular decomposition of many chemicals. In [1] , the unimolecular thermal decomposition mechanism of anti-N,N’-Dinitrourea is studied by an in situ pyrolytic Fourier transform infrared spectroscopy with the temperature program and density functional theory calculations. The thermal unimolecular decomposition of dichloroketene is studied experimentally and computationally in [2] . The authors use the analysis of the experimental data and the computational models to demonstrate that thermal decomposition is a major pathway of destruction for dichloroketene in combustion systems. In [3] , the unimolecular decomposition of the phenyl radical and ortho-benzyne is examined by ab initio quantum chemical calculations, Rice-Ramsperger-Kassel-Marcus calculations, and numerical simulation of shock tube pyrolysis of phenyl and benzene. In [4] , the unimolecular decomposition study of dibromomethoxy radical, CHBr2O, and its isomeric hydroxy dibromomethyl radical, CBr₂OH, are carried out using ab initio electronic molecular structure methods. The thermal unimolecular decomposition of propynal is investigated behind reflected shock waves in [5] . The authors conclude that the decomposition proceeds via the molecular path to produce acetylene and carbon monoxide. Recently in [6] , an experimental and modelling study of the thermal decomposition of methyl decanoate is performed in a jet-stirred reactor at constant temperature and pressure. A model for the thermal decomposition of methyl decanoate is generated using the software EXGAS. The model reproduces fairly well the conversion of the reactant and the mole fractions of the reaction products.

The present study addresses the unimolecular thermal decomposition of a chemical passing through a parallel plate reactor with four transverse heated rods, which is investigated. The compound to be decomposed is dissolved in water. The water with the dissolved compound first enters the reactor from the left then passes heated circular cylinders before exiting from the right side and hence the reacting fluid is heated as it passes the transverse cylinders. The proposed model is numerically simulated using Galerkin weighted residual finite element method [7] -‎ [10] . Recently in [11] - [13] , the Galerkin weighted residual finite element technique has been efficiently used to model the natural convection in both light and heavy water in a vessel containing heated cylindrical obstacles, while in ‎ [13] , the method has been powerfully applied to model the laminar buoyancy convection inside a square cavity containing an obstacle.

The numerical results are presented graphically in terms of contour plots and curves at the longitudinal axis of the reactors for various values of water inlet velocity and rods temperature when the reaction energy is considered and when is neglected.

2. Problem Formulation

The three-dimensional (3-D) representation of the reactor geometry is shown in Figure 1. The problem is formulated in two-dimensional (2-D) domain without dramatically reducing the validity of the simulation because of neglecting any edge effects from the reactor walls; moreover the velocity between the side walls is expected to be close to constant for such geometry, short inlet side of the reactor is considerably wider than it is high, [14] . So, the model can be described using 2-D representation as shown in Figure 2.

The computational domain is considered as follows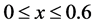, 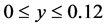and the four circular rods of radius equal 0.01 are centered at the following points: (0.1, 0.04), (0.2, 0.08), (0.3, 0.04) and (0.4, 0.08). All dimensions are given in meters. The reactant fluid enters the reactor at constant temperature 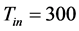and constant normal velocity. The uniform temperature of the rods is assumed to be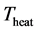. Here 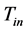is less than. There is no viscose stress at all the free boundaries and the pressure is considered to be zero there. The

rods are considered with no slip as walls. The water and the reaction physical properties used in the simulation are listed in Table 1.

The physical properties of water are assumed to be constant and don’t depend on the thermal field.

3. Mathematical Formulation

In the current problem, we have considered that the water flow is a steady-laminar one. The gravitational force and radiation effect are neglected here. The governing equations that describe the present model are incompressible Navier-Stokes equations, energy balance equation, convection and diffusion equation and equations related to the chemistry of the problem.

Consider the heat sensitive chemical “A” (dissolved in water) undergoes thermal decomposition into fragments “B” according to the unimolecular reaction described by Equation (1). The rate constant [1/s] is determined according to the Arrhenius equation [15] [16] :

(4)

where 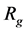is the gas constant (8.314) and T is the temperature.

The reaction rate can be calculated from the following equation:

(5)

where is the concentration of the reactant “A” in water.

In addition, if the decomposition reaction is considered to be exothermic, then the rate of the expelled energy during the reaction Q is given by:

(6)

In the present model the fluid flow is described by 2D steady state incompressible Navier-Stokes equations:

(7)

(8)

(9)

where u and v are the velocities in the x and y directions, respectively and p is the pressure.

We used this formulation because the flow regime is laminar and the density is assumed to be constant. It’s known that the Reynolds number indicates whether a flow regime is laminar or turbulent. In the present simulation, we will simulate the decomposition at two inlet normal velocities and. The Reynolds number can be calculated from the following formula:

where d is characteristic length which is equal to 0.12 for the present model. By calculating the Reynolds numbers in the considered cases, we can conclude that the Reynolds numbers are well within the limits of the lami- nar regime which is Re < 2000. Moreover, assuming that water density is constant and doesn’t depend on the thermal field, the incompressible Navier-Stokes Equations (7)-(9) are appropriate to model the flow.

Considering the heat transfer is done through conduction and convection, the next energy balance equation used to model the energy transport in the reactor

(10)

where Q is a sink or source term, which here is the energy expelled during the reaction. So, if the reaction isn’t exothermic then Q = 0, whenever if the reaction is exothermic then. In case of, the rate constant is estimated at suitable average temperature for simplicity.

The mass transfer of the compound “A” in the reactor is governed by the convection and diffusion equation:

(11)

where denotes the reaction term. Equation (11) considers the species “A” is diluted in water.

The proper boundary conditions of the considered problem are listed below:

at the surfaces of the reactor walls and heated rods.

at the surfaces of the heated rods.

4. Methodology

The numerical technique has been used to solve the Navier-Stokes, energy balance and mass transport Equations (7)-(11) subject to the given boundary conditions is the finite element formulation based on the Galerkin weighted residual method. The applications of this method are well described in ‎‎ [11] -‎ [13] . Based on the considered technique, the overall domain is discretized into a number of appropriate finite elements as a grid. Here, the given domain is composed into non-uniform biquadratic elements using commercially available grid generators ANSYS. Figure 3 shows the mapping of the present domain by biquadratic elements as an unstructured mesh. The resolution of the grid near the rods is prepared finer to ensure capturing the necessary phenomena there accurately.

As illustrated in ‎ [17] - [19] , the continuity Equation (7) can be used as a constraint due to mass conservation and hence the pressure distribution can be obtained using this constraint. In order to solve Equations (8)-(11), a penalty finite element formulation is used. The pressure p can be eliminated in Equations (8) and (9) using the constraint equation,

(12)

where is a penalty parameter [18] . The continuity equation (7) is satisfied for large values of. Typical value of that give up consistent solution is ‎ [17] -‎ [19] .

Using Equation (12), the momentum balance equations (8) and (9) reduce to

(13)

(14)

Expanding the velocity components (u,v), temperature (T) and concentration () by using basis set as,

and (15)

where N is the number of nodes for each biquadratic element.

Based on the Galerkin weighted residual finite element method, the weight functions are identical to the elements shape functions and hence the nonlinear residual equations related to Equations (13), (14), (10) and (11), respectively, at nodes of internal element domain are:

(16)

(17)

(18)

(19)

Biquadratic shape functions with three point Gaussian quadrature is used to calculate the integrals in the residual Equations (16)-(19). In Equations (16) and (17), the second integral containing the penalty parameter are evaluated with two point Gaussian quadrature (reduced integration penalty formulation [17] - [19] ). It has been found that lowering the integration order is essential to avoid ill-conditioning of the Jacobian for large values of.

The non-linear residual equations are solved using Newton-Raphson method to determine the coefficients of the expansions in Equation (15). The boundary conditions are incorporated into the assembled global system of nonlinear equations to make it determinate. norm for the residual vectors is used for the stopping criteria of the Newton-Raphson iterative process. The process is terminated with the convergence criterion

Eight node biquadratic elements have been used with each element. Before evaluating Gauss integration, the coordinate x − y must be mapped into of the natural coordinate due to the irregularity of the element shape. The transformation between (x, y) and coordinates can be defined by

and (20)

where are the x, y coordinates of the k nodal points and is the local basis function in domain. The eight basis functions used are (serendipity type [20] [21] )

(21)

Consequently, the domain integrals in the residual equations are approximated using eight node biquadratic basis functions in domain using Equations (20) and (21).

In the present study, the model validation is justified by studying the number of iterations needed for convergence and error analysis of the finite element method.

5. Convergence of Solution

In order to verify the numerical validation of the numerical scheme, the convergence history for calculations is presented in Figure 4. The convergence history is represented in terms of the residuals of u-momentum, v-mo- mentum, energy balance and mass balance versus number of iterations. A converged solution could be calcu-

lated within about 50 iterations. The calculations were performed on a Pentium IV computer and a typical run for a solution required about 2 CPU minutes.

6. Results and Discuss

Equations (10), (11), (13) and (14) with the given boundary conditions have been solved numerically using a penalty finite element method based on Galerkin weighted residuals. The computational domain in coordinates consists of 1280 biquadratic elements. The jump discontinuity in Dirichlet type of boundary conditions at the corner points (at inlet and outlet) correspond to computational singularity. In the present investigation, Gaussian quadrature based finite element method gives the smooth solutions at the interior domain including the corner regions as evaluation of residuals depends on interior gauss points and hence the effect of corner singularity are less pronounced in the final solution.

The results have been presented graphically in both contour plots and one-dimensional representation in order to illustrate the effects of the reaction energy, heated rods temperature and fluid inlet velocity on the thermal field and decomposition of heat sensitive chemical “A”. The numerical results are displayed as contour plots in Figure 5 while the results in a 1-D representation are displayed in Figure 10. The simulation is done in case of the reaction energy is considered i.e. and when it is neglected i.e. H = 0. Figure 5 illustrate the influences of the inlet velocity on velocity field, thermal field and concentration of the chemical “A”, respectively at the same heated rods temperature. The effect of the rods temperature on the decomposition of chemical “A”, at the same inlet velocity is illustrated in Figure 9. The influence of the reaction energy on thermal field of the reactant fluid at and is shown in Figure 7.

As shown in Figure 5, the fluid velocity increases in an oscillating manner as it passes around the heated rods. This increasing is due to the narrowness caused by circular rods. From Figure 6, it can be noticed that the temperature of the reactant fluid increases as it passes the heated rods. The second result can be drawn from Figure 6 is that as the inlet velocity increases the rate of increasing of the temperature will decrease and hence the rate of the decomposition of the compound “A” will be decreased. Comparing Figure 6 and Figure 7 will lead to that the thermal field of the reactant fluid is majorly influenced by the energy expelled during the reaction H, whoever it is slightly influenced by the inlet velocity. Figure 8 shows that at the same and H, the concentration of the chemical “A” decreases as increases. In addition, the molecules of “A” vanish at the outlet of the reactor for, while some molecules remain dissolved in water for.

Thus, the decomposition of the compound “A” is greatly affected with the fluid inlet velocity. Also, in the absence of the reaction energy i.e. H = 0, the decomposition of “A” will be influenced by the temperature of the transverse heated rods as illustrated in Figure 9. As expected that the higher, the less at the reactor outlet. From the previous results, one can notice the consistency between the results and physical and chemical thermodynamic.

A comparison between Figure 9(a) and Figure 8(a) will demonstrate the role of the energy expelled during the reaction on the decomposition process. The comparison illustrates that at the same and, the rate of decreasing of the compound “A” concentration increases when considering the energy of the reaction. This can be shown in that the molecules of “A” are fully decomposed at the outlet of the reactor when, while some molecules remain dissolved in the absence of reaction energy. Therefore, the decomposition of the exothermic reactions is greater than the decomposition of not exothermic ones as expected from physical and chemical thermodynamic.

All the previous discussed results can be deduced by examining the results in the 1-D representation shown in Figure 10. The results in the 1-D graphs are plotted at the longitudinal axis of the reactors i.e. at y = 0.06. Figure 10 show the profile of the u-velocity component along the longitudinal axis for two inlet velocities. It can be shown that velocity increases in a fluctuating profile as it passes between the rods.

The influences of the inlet velocity, rods temperature and energy expelled during the reaction on the thermal field can be summarized form Figure 11. Figure 11(a) and Figure 11(b) illustrate that the increasing in the inlet velocity will decrease the temperature of reactant fluid. In the absence of the reaction energy when, the temperature of the fluid in the reactor at the outlet is about 305 when, however it reaches 340 when as shown in Figure 11(c). When considering the reaction energy, the temperature will reach 315 when and as shown in Figure 11(b) and Figure 11(d). Totally, Figure 11 demonstrates that the thermal field and natural convection in the fluid are greatly influenced by inlet velocity, temperature of heated rods and type of the reaction.

Figure 12 illustrates various effects of inlet velocity, rods temperature and energy of the reaction on the concentration of the heat sensitive compound “A” and hence on the decomposition of “A”. Figure 12(a) and Figure 12(b), display the effects of inlet velocity on concentration of chemical “A” at with and without the reaction energy.

From Figure 12(a) and Figure 12(b), it can be shown that the concentration of “A” at the outlet is about half the concentration at the inlet when while in case of low inlet velocity, , the concentration at the outlet is about 50 for H = 0 and about zero for. This can be summarized in that the lower inlet velocity, the greater amount of the chemical “A” will be decomposed. Figure 12(c) shows the effect

of the rods temperature on concentration of “A”.

Comparing Figure 12(a) and Figure 12(b) with Figure 12(c), will summarize that decomposition process is majorly influenced by and slightly influenced by. The effect of the reaction type on the decomposition process is illustrated in Figure 12(d). It is clear that, the concentration of “A” is about zero at last heated rod, x=0.4, for exothermic reaction however the concentration is about 100 in case of a not exothermic one at the same position and inlet velocity. Finally, Figure 12 demonstrates that the concentration of the chemical “A” and hence the decomposition process are significantly influenced by inlet velocity and the reaction type.

7. Conclusions

The main objective of the current investigation is to study the influences of reactant fluid inlet velocity, rods temperature and reaction type on the unimolecular thermal decomposition of a chemical dissolved in water inside a parallel-plate reactor having four transverse heated rods. The penalty Galerkin weighted residuals finite element method is used to obtain smooth and reliable solutions for the considered model. Summarizing all the results discussed above will lead to the following conclusions:

1. The decomposition of the dissolved chemical is greatly affected by the fluid inlet velocity.

2. Decreasing the fluid inlet velocity will increase the amount of the chemical being decomposed.

3. The decomposition of the chemical is significantly influenced by the reaction type from the thermal sight.

4. The decomposition process is slightly influenced by the temperature of circular rods.

5. The increasing in the fluid velocity and temperature along the reactor is of an oscillating type due to the consequently heated rods.

6. The obtained results are largely consistent with physical and chemical thermodynamic.

Acknowledgements

The author would like to thank Deanship of Scientific Research at Majmaah University, Saudi Arabia for the financial grant received in conducting this research.

Cite this paper

Mohamed M.Mousa,11, (2016) Finite Element Simulation of an Unimolecular Thermal Decomposition inside a Reactor. Journal of Applied Mathematics and Physics,04,328-340. doi: 10.4236/jamp.2016.42040

References

Nomenclature