Journal of Applied Mathematics and Physics
Vol.03 No.11(2015), Article ID:61504,18 pages
10.4236/jamp.2015.311173
Exactly Solvable Schrödinger Equation with Hypergeometric Wavefunctions
J. Morales1*, J. García-Martínez2, J. García-Ravelo3, J. J. Peña1
1Universidad Autónoma Metropolitana-Azc., DCB-Area de FAMA, Sn Pablo 180, Mexico City, México
2Tecnológico de Estudios Superiores de Ixtapaluca, División de Ingeniería Informática e Ingeniería Biomédica, Carretera Ixtapaluca Coatepec Km. 7, Mexico City, México
3Escuela Superior de Física y Matemáticas, IPN-Zacatenco, UP Adolfo López Mateos, México

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 13 October 2015; accepted 23 November 2015; published 26 November 2015

ABSTRACT
In this work, the canonical transformation method is applied to a general second order differential equation (DE) in order to trasform it into a Schrödinger-like DE. Our proposal is based on an auxiliary function g(x) which determines the transformation needed to find exactly-solvable potentials associated to a known DE. To show the usefulness of the proposed approach, we consider explicitly their application to the hypergeometric DE with the aim to find quantum potentials with hypergeometric wavefunctions. As a result, different potentials are obtained depending on the choice of the auxiliary function; the generalized Scarf, Posh-Teller, Eckart and Rosen-Morse trigonometric and hyperbolic potentials, are derived by selecting g(x) as constant and proportional to the P(x) hypergeometric coefficient. Similarly, the choices 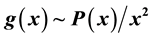 and
and 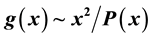 give rise to a class of exactly-solvable generalized multiparameter exponential-type potentials, which contain as particular cases the Hulthén, Manning-Rosen and Woods-Saxon models, among others. Our proposition is general and can be used with other important DE within the frame of applied matematics and physics.
give rise to a class of exactly-solvable generalized multiparameter exponential-type potentials, which contain as particular cases the Hulthén, Manning-Rosen and Woods-Saxon models, among others. Our proposition is general and can be used with other important DE within the frame of applied matematics and physics.
Keywords:
Canonical Transformation, Schrödinger-Like Equation, Hypergeometric DE, Exactly-Solvable Potentials

1. Introduction
Exactly and quasi-exactly solvable potential models are important in practically any field of theoretical quantum chemistry and physics for two principal reasons: first, they are useful to understand the behavior of quantum systems and second, can be used as a basis to study problems that can only be treated using perturbative and nonperturbative procedures. In spite of the above, the exactly solvable Schrödinger equations are rather scanty and in their research different analytical or operational approaches have been used. Also, the well known exactly- solvable Scarf, Eckart, Rosen-Morse I and II, Poschl-Teller I and II as well as Hulthén, Manning-Rosen and Woods-Saxon potentials, all they have, as common feature, hypergeometric wavefunctions. Similarly, the harmonic oscillator, Morse, Coulomb or Kratzer potential models have confluent hypergeometric solutions. Consequently, it becomes clear that the exact solution for the Schrödinger equation is reduced to the study of hypergeometric and/or confluent hypergeometric Differential Equations (DE). At this regard, many efforts have been conducted to find the intermapping between different solvable potentials [1] [2] with the aim to give a unified treatment of partner potentials [3] . For example, in the case of potentials with the hypergeometric wavefunctions, the hexagonal diagram proposed by Cooper et al. [4] is very useful to show how all the shape invariant potentials are inter-related. Also, it has been proposed a pre-potential approach to study of Eckart-type potentials [5] and a five-parameter exponential-type potential to unify the treatment of exactly solvable trigonometric potential models [6] -[8] . Furthermore, to find exactly solvable Schrödinger equations different methods based on Supersymetric Quantum Mechanics (SUSY-QM) [9] , Asymptotic Iteration Method (AIM) [10] and on the transformation of a Schrödinger equation into a hypergeometric-type DE by the Nikiforov-Uvarov (NU) [11] approach, have been used. In this work, we present a proposal that can be considered inverse to the NU method. However, instead of transforming a DE into a Schrödinger equation we consider the transformation of a general homogeneous linear second order DE to their canonical form. Obviously, the general DE has as particular cases the hypergeometric and confluent hypergeometric DE. For that reason, this work aims at finding solvable potentials with hypergeometric wavefunctions leaving the treatment of models with confluent hypergeometric solutions elsewhere [12] . Thus, the proposed approach to transform a general DE into a Schrödinger-like equation is given in next section by means of the canonical transformation method given in the Appendix. The application of the present proposal is given in Section 3, where we consider the hypergeometric DE by means of an auxiliary function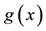 , defined in Section 2, that indicates the required transformation. That is, as will be shown, each possibility of
, defined in Section 2, that indicates the required transformation. That is, as will be shown, each possibility of 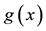 leads to different generalized potentials which are reduced to well known particular cases. Finally, in Section 4 we presents the concluding remarks emphasizing that our proposition is general for which can be directly applied to other important DE.
leads to different generalized potentials which are reduced to well known particular cases. Finally, in Section 4 we presents the concluding remarks emphasizing that our proposition is general for which can be directly applied to other important DE.
2. Transformation of a General DE into a Schrödinger-Like Equation
According to the proposition given in Equation (A5), the generalized canonical transformation of Equation (A1) becomes
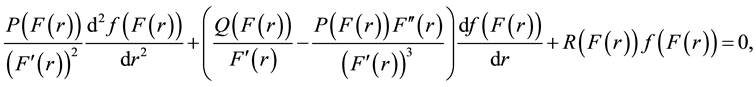 (1)
(1)
that can be rewritten as
 (2)
(2)
where
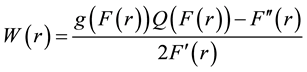 (3)
(3)
and
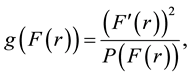 (4)
(4)
that will be referred as auxiliary function hereafter. Consequently, from the above, the variable r is given by
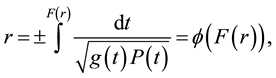 (5)
(5)
in such a way that Equation (A5) is feasible on condition to have the inverse function
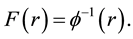 (6)
(6)
Furthermore, the general transform given in Equation (A6) can be rewritten as
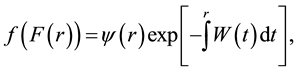 (7)
(7)
where we have used the auxiliary function and the fact that
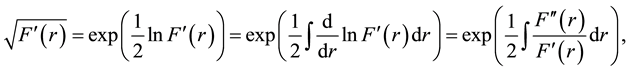 (8)
(8)
such that
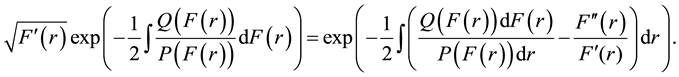 (9)
(9)
Consequently, by substituting Equation (7) into Equation (2), the generalized canonical form of Equation (A1) will be
 (10)
(10)
At this point, it should be noticed that above equation can be identified with a Schrödinger-like equation where the 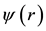 wavefunction can be obtained from Equation (7) on condition that coefficients
wavefunction can be obtained from Equation (7) on condition that coefficients 


being 

In short, it is worth noting that 





3. Application to the Hypergeometric DE
To show the usefulness of the approach given in above section, in the search of exactly-solvable Schrödinger equations, let us apply the above results to the hypergeometric DE

whose solution is [13]

where 



As mentioned before, depending on the choice of



where we have used the explicit form of function











3.1. Generalized Potentials from g(x) Constant
Let us consider the identity

to rewrite Equation (5) as

with the purpose to use the integral [14]

That is, the above integral and the choice of 

allows to evaluate the integral of Equation (16) as

Consequently, in this case the corresponding transformation is

leading to the particular cases + and − specified by

Thus, according to Equation (3), 

which means

and

Thus, as mentioned before, the potential function 


leading to the corresponding generalized potentials

with eigenvalues

and eigenfunctions

Also, in order to have physically acceptable wavefunctions, the original parameters a, b and c are redefined as

with

as well as their respective wavefunctions

with energy spectra

At this point, is important to notice that particular cases

and

are identified with the well known trigonometric 


and

respectively, where 



As can be proved, the plus (+) case leads to 

which indicates that the corresponding transformation is

Then, according to Equation (3), in this case 

leading, from Equation (11), to the potential

with eigenvalue

and eigenfunction

Finally, using the conditions for physically acceptable wavefunctions one obtains

that leads to the potential

with eigenfunctions

and energy spectra

that coincides with the well known Posch-Teller potential.
3.2. Generalized V(r) from g(x) Proportional to P(x)
Similarly to the cases considered in above section, the choice of

can be worked by means of the integrals

In fact, the use of Equation (49) lets write Equation (16) as

leading to the corresponding transformation

So, according to Equation (3)

Thus, the potential function V(r) and the eigenvalue E can be identified from Equation (11) as

to obtain the corresponding generalized potentials

with eigenvalue

and wavefunction

As before, with the aim to have physically acceptable solutions it becomes necessary to redefine the original parameters a, b and c as follow

with 


with their corresponding wavefunctions

and energy spectra

where

At this point, is important to notice that potential 

corresponds to the Rosen-Morse II hyperbolic potential and

to the exactly solvable Eckart potential. Also, we want to point out that 


and

respectively. Similarly to the cases analyzed in section III.1), the question is now; How can obtain the Rosen-Morse II trigonometric potential? To answer that question, we are going to use the same choice of 


that together with Equation (49) in Equation (16) permit us to obtain

Thus, with the aid of the identity

the corresponding transformation is

Consequently, according to Equation (3)

such that

leading to

with eigenvalue

and eigenfunction

Similarly, to have physically acceptable wavefunctions the original parameters a, b and c are defined as

where 

with energy spectra

and eigenfunctions

where

Specifically, the 


and

with their respective wavefunctions

and

with the same energy spectra. At this point, we want to notice that potential 

3.3. A class of Multiparameter Exponential-Type Potential
a). Option with
According to the third option for 

In fact, by choosing the minus sign in Equation (5) and the down integral limit as a new parameter q, one obtains

from which

being 


leading, from Equation (11), to

Thus, by defining

and

it becomes possible to identify the potential

the eigenvalue

and, from Equation (7), the eigenfunction

In what follow, the parameters a,b and c will be calculated by considering the boundary conditions of the system in order to have physically acceptable wavefunctions. For example, by combining Equation (89) and Equation (90) one obtains

with

Thus, to have a node in 




and

On the other hand, by using Equation (94) in Equation (89) we obtain

and

Also, since the hypergeometric function of Equation (93) is an infinite series, the condition

leads to a polynomial of n degree in the variable


that 

These assumptions on the original parameters {a, b, c} assure that boundary conditions are fulfilled, leading to a physically acceptable wavefunction for the Schrödinger equation under consideration. Additionally, the energy spectra for the potential 

with the corresponding wavefunctions

It should be pointed out that in this case the potential V(r) has a minimum value

in

on condition that

since in this case the argument of the logarithm function, given in Equation (105), is always positive. Consequently, Equations (104)-(106) ensures that potential V(r) is attractive with a infinite wall in
values of A, B, and C. For example, the choice of 



which is identified with the standard Hulthén potential with eigenvalues [15] [16]

and eigenfunctions

In a similar way, the selection 

Hulthén potential already given by Morales et al., [17] . Also, the selection 




with energy spectra

and wavefunctions

Another important exactly-solvable exponential potential that have hypergeometric wavefunctions is the Woods-Saxon potential which has been worked using the Numerov method for the standard model [19] or by means of the Nikiforov-Uvarov procedure for the generalized case [20] . According to our results, one can show that the generalized Woods-Saxon potential is obtained as particular case of our proposal when choosing 





However, due to the fact that the approach considered until now in this work is consistent with





with

and

as well as

Thus, by using Equation (114) and the negative of Equation (89) we obtain

and

with the condition 


and

b). Option with
Similarly to the above case, in this new situation one have

that leads to the transformation

where 

that, from Equation (3), lets write

In this new situation, by considering the identities

and

as well as

one find the multiparameter exponential-type potential

with eigenvalue

and eigenfunction

At first glance, the potential of Equation (129) can be considered as a new one and however it should be noticed that it can be written as

That is, the above 
approximation schemes proposed to



other particular radial potentials can be derived from our proposal as, for example, the recently considered Manning-Rosen potential [23] which, as explained before, comes from Equation (91).
4. Concluding Remarks
In this paper, we present a method to obtain the general canonical form of second order differential equations on the field of theoretical physics. The procedure is similar to the method proposed by Levai [24] and however we consider a general DE to be converted into a Schrödinger-like equation. The algorithm we propose, makes use of an auxiliary function 







Acknowledgements
This work was partially supported by the projects UAM-A-CBI-2232004 and 009. JGR thanks to the Instituto Politécnico Nacional for the financial support given through the COFAA-IPN project SIP-200150019. JGM acknowledges to the IPN-ESFM, for the hospitality during his PhD studies in Science and Technology.
Cite this paper
J.Morales,J.García-Martínez,J.García-Ravelo,J. J.Peña, (2015) Exactly Solvable Schrödinger Equation with Hypergeometric Wavefunctions. Journal of Applied Mathematics and Physics,03,1454-1471. doi: 10.4236/jamp.2015.311173
References
- 1. Sukumar, C.V. (1985) Supersymmetric Quantum Mechanics of One-Dimensional Systems. Journal of Physics A: Mathematical and General, 18, 2917-2936.
http://dx.doi.org/10.1088/0305-4470/18/15/020 - 2. De, R., Dutt, R. and Sukhatme, U. (1992) Mapping of Shape Invariant Potentials under Point Canonical Transformations. Journal of Physics A: Mathematical and General, 25, L843-L850.
http://iopscience.iop.org/0305-4470/25/13/013 - 3. Setare, M.R. and Karimi, E. (2008) Mapping of Shape Invariant Potentials by the Point Canonical Transformation. International Journal of Theoretical Physics, 47, 891-897.
- 4. Cooper, F., Khare, A. and Sukhatme, U. (1995) Supersymmetry and Quantum Mechanics. Physics Reports, 251 267-385.
http://dx.doi.org/10.1016/0370-1573(94)00080-M - 5. Ho, C.-L. (2009) Simple Unified Derivation and Solution of Coulomb, Eckart and Rosen-Morse Potentials in Prepotential Approach. Annals of Physics, 324, 1095-1104.
http://dx.doi.org/10.1016/j.aop.2008.10.004 - 6. Jia, C.-S., Diao, Y.-F., Li, M., Yang, Q.-B., Sun, L.-T. and Huang, R.-Y. (2004) Mapping of the Five-Parameter Exponential-Type Potential Model into Trigonometric-Type Potentials. Journal of Physics A: Mathematical and General, 37 11275-11284.
http://dx.doi.org/10.1088/0305-4470/37/46/012 - 7. Jia, C.-S., Yi, L.-Z., Zhao, X.-Q., Liu, J.-Y. and Sun, L.-T. (2005) Systematic Study of Exactly Solvable Trigonometric Potentials with Symmetry. Modern Physics Letters A, 20, 1753-1762.
http://dx.doi.org/10.1142/S0217732305017081 - 8. Jia, C.-S., Liu, J.-Y., Sun, Y., He, S. and Sun, L.-T. (2006) A Unified Treatment of Exactly Solvable Trigonometric Potential Models. Physica Scripta, 73, 164-168.
http://iopscience.iop.org/1402-4896/73/2/006 - 9. Cooper, F., Khare A. and Sukhatme, U. (2001) Supersymmetry in Quantum Mechanics. World Scientific Publishing Co Pte Ltd.
- 10. Ciftci, H., Hall, R.L. and Saad, N. (2003) Asymptotic Iteration Method for Eigenvalue Problems. Journal of Physics A: Mathematical and General, 36, 11807-11816.
http://dx.doi.org/10.1088/0305-4470/36/47/008 - 11. Nikiforov, A.F. and Uvarov, V.B. (1988) Special Functions of Mathematical Physics. Birkhauser, Basel.
http://dx.doi.org/10.1007/978-1-4757-1595-8 - 12. Peña, J.J., Morales, J., García-Martínez, J. and García-Ravelo, J. (2008) Exactly Solvable Quantum Potentials with Special Functions Solutions. International Journal of Quantum Chemistry, 108, 1750-1757.
http://dx.doi.org/10.1002/qua.21611 - 13. Abramowitz, M. and Stegun, I.A. (1972) Handbook of Mathematical Functions. Wiley and Sons, New York.
- 14. Granville, W.A., Smith, P.F. and Longley, W.R. (1941) Elements of the Differential and Integral Calculus. Ginn & Co., Boston.
- 15. Hulthén, L. (1942) On the Characteristic Solutions of the Schrñdinger Deuteron Equation. Arkiv fñr Matematik Astronomi och Fysik A, 28, art 5: 1-12.
- 16. Chen, G. (2004) Shape Invariance and the Supersymmetric WKB Approximation for the Generalized Hulthén Potential. Physica Scripta, 69, 257-259.
http://dx.doi.org/10.1238/physica.regular.069a00257 - 17. Morales, J., Peña, J.J. and Morales-Guzman, J.D. (2000) The Generalized Hulthén Potential. Theoretical Chemistry Accounts, 104, 179-182.
http://dx.doi.org/10.1007/s002140000130 - 18. Ahmed, S.A.S. and Buragohain, L. (2010) Exactly Solved Potentials Generated from the Manning-Rosen Potential Using Extended Transformation Method. Electronic Journal of Theoretical Physics, 7, 145-154.
- 19. Fatah, A.H. (2012) Calculation of the Eigenvalues for Wood-Saxon’s Potential by Using Numerov Method. Advances in Theoretical and Applied Mechanics, 5, 23-31.
- 20. Berkdemir, C., Berkdemir, A. and Sever, R. (2005) Polynomial Solutions of the Schrñdinger Equation for the Generalized Woods-Saxon Potential. Physical Review C, 72, 027001-1-027001-4.
- 21. Gñnül, B. and Kñksal, K. (2007) Solutions for a Generalized Woods-Saxon Potential. Physica Scripta, 76, 565-570.
http://dx.doi.org/10.1088/0031-8949/76/5/026 - 22. Falaye, B.J., Oyewumi, K.J., Ibrahim, T.T., Punyasena, M.A. and Onate, C.A. (2013) Bound State Solutions of the Manning-Rosen Potential. Canadian Journal of Physics, 91, 98-104. http://dx.doi.org/10.1139/cjp-2012-0330
- 23. Nasser, I., Abdelmonem, M.S. and Abdel-Hady, A. (2013) The Manning-Rosen Potentials Using J-Matrix Approach. Molecular Physics, 111, 1-8.
http://dx.doi.org/10.1080/00268976.2012.698026 - 24. Lévai, G. (1989) A Search for Shape-Invariant Solvable Potentials. Journal of Physics A: Mathematical and General, 22, 689-702.
http://dx.doi.org/10.1088/0305-4470/22/6/020 - 25. Peña, J.J., García-Martínez, J., García-Ravelo, J. and Morales, J. (2014) l-State Solutions of Multiparameter Exponential-Type Potentials. Journal of Physics: Conference Series, 490, 012199.
http://dx.doi.org/10.1088/1742-6596/490/1/012199 - 26. Arfken, G. and Weber, H. (2005) Mathematical Methods for Physicists. 6th Edition, Elsevier AP, Boston.
- 27. Polyani, A.D. and Zaistev, V.F. (2003) Handbook of Exact Solutions for Ordinary Differential Equations. 2nd Edition, Chapman& Hall/CRC, Boca Raton, New York.
Appendix
The general second order DE

is transformed into their standard canonical form [26]

by means of the transformation

i.e.

where apostrophes indicates derivative with respect to the argument.
In order to have a generalized canonical transformation of Equation A1, we consider the variable change

to obtain the general transformation [27]

Consequently, one have

being

where

It will be noticed that, for the particular case 
NOTES
*Corresponding author.






