Journal of Applied Mathematics and Physics
Vol.03 No.10(2015), Article ID:60745,26 pages
10.4236/jamp.2015.310160
Asymptotic Boundary Forms for Tight Gabor Frames and Lattice Localization Domains
H. G. Feichtinger1, K. Nowak2, M. Pap3
1Faculty of Mathematics, University Vienna, Wien, Austria
2Department of Computer Science, Drexel University, Philadelphia, PA, USA
3Faculty of Sciences, University of Pécs, Pécs, Hungary
Email: hans.feichtinger@univie.ac.at, knowak1248@gmail.com, papm@gamma.ttk.pte.hu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 September 2015; accepted 26 October 2015; published 29 October 2015
ABSTRACT
We consider Gabor localization operators  defined by two parameters, the generating function
defined by two parameters, the generating function  of a tight Gabor frame
of a tight Gabor frame , indexed by a lattice
, indexed by a lattice , and a domain
, and a domain  whose boundary consists of line segments connecting certain points of
whose boundary consists of line segments connecting certain points of . We provide an explicit formula for the boundary form
. We provide an explicit formula for the boundary form , the normalized limit of the projection functional
, the normalized limit of the projection functional , where
, where  are the eigenvalues of the localization operators
are the eigenvalues of the localization operators  applied to dilated domains
applied to dilated domains , R is an integer and
, R is an integer and  is the area of the fundamental domain. The boundary form expresses quantitatively the asymptotic interactions between the generating function
is the area of the fundamental domain. The boundary form expresses quantitatively the asymptotic interactions between the generating function  and the oriented boundary
and the oriented boundary  from the point of view of the projection functional, which measures to what degree a given trace class operator fails to be an orthogonal projection. Keeping the area of the localization domain
from the point of view of the projection functional, which measures to what degree a given trace class operator fails to be an orthogonal projection. Keeping the area of the localization domain  bounded above corresponds to controlling the relative dimensionality of the localization problem.
bounded above corresponds to controlling the relative dimensionality of the localization problem.
Keywords:
Toeplitz Operators, Phase Space Localization, Tight Gabor Frames, Semi-Classical Limit

1. Main Results and Their Context
We start by formulating the main results of this paper. Let 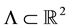 be a lattice, i.e. a discrete co-compact subgroup of
be a lattice, i.e. a discrete co-compact subgroup of![]() , satisfying condition
, satisfying condition![]() , where
, where ![]() denotes the area of the fundamental domain of
denotes the area of the fundamental domain of![]() . For a function
. For a function ![]() and
and ![]() we define
we define![]() . Let the system
. Let the system![]() , where
, where ![]() is a fixed function, be a tight Gabor frame, i.e. we assume that for every
is a fixed function, be a tight Gabor frame, i.e. we assume that for every ![]()
![]() (1)
(1)
where the convergence of the sum is understood in the unconditional norm sense. Function ![]() is called the generating function of a tight Gabor frame
is called the generating function of a tight Gabor frame![]() . An operator
. An operator![]() , acting on
, acting on![]() , and of the form
, and of the form
![]() (2)
(2)
is called a Gabor multiplier of localization type, if its symbol b, defined on the lattice Λ, is non-negative and summable. It can be easily verified that Gabor multipliers of localization type are non-negative, trace class, and that
![]()
and the operator norm of ![]() satisfies
satisfies
![]()
The projection functional PF is defined on positive definite, trace class operators T, with their operator norm bounded above by 1, via the formula
![]() (3)
(3)
where ![]() are the eigenvalues of T. The projection functional measures the extend by which the operator T fails to be an orthogonal projection. It takes non-negative values and it vanishes on the space consisting of finite dimensional orthogonal projections. A collection of line segments
are the eigenvalues of T. The projection functional measures the extend by which the operator T fails to be an orthogonal projection. It takes non-negative values and it vanishes on the space consisting of finite dimensional orthogonal projections. A collection of line segments![]() ,
, ![]() each of them starting and ending at a point of Λ is called a Λ cycle if the union
each of them starting and ending at a point of Λ is called a Λ cycle if the union ![]() forms a closed continuous line without self intersections. A bounded, connected and closed subset
forms a closed continuous line without self intersections. A bounded, connected and closed subset ![]() is called a Λ domain if its boundary consists of a finite family of Λ cycles
is called a Λ domain if its boundary consists of a finite family of Λ cycles![]() ,
, ![]() satisfying condition
satisfying condition ![]() for
for![]() . We say that a function
. We say that a function ![]() satisfies condition Φ if
satisfies condition Φ if
Φ: ![]() .
.
For a Λ domain ![]() and a generating function
and a generating function ![]() of a tight Gabor frame
of a tight Gabor frame ![]() satisfying condition Φ the boundary form
satisfying condition Φ the boundary form ![]() is defined by the formula
is defined by the formula
![]() (4)
(4)
where![]() ,
, ![]() are the line segments constituting the boundary of Ω,
are the line segments constituting the boundary of Ω, ![]() is the unit vector orthogonal to
is the unit vector orthogonal to ![]() directed outside Ω,
directed outside Ω, ![]() ,
,![]() .
.
The projective metaplectic representation defined on ![]() provides the most natural way to deal with linear changes of coordinates of the TF-plane
provides the most natural way to deal with linear changes of coordinates of the TF-plane![]() . Its definition and its basic properties are reviewed in Section 4. It came to us as a surprise that the boundary form BF, representing the limit value of the projection functional PF with respect to dilation factors of the localization domain tending to infinity, is invariant with respect to the action of the projective metaplectic representation. Many geometric and numerical studies of lattices in
. Its definition and its basic properties are reviewed in Section 4. It came to us as a surprise that the boundary form BF, representing the limit value of the projection functional PF with respect to dilation factors of the localization domain tending to infinity, is invariant with respect to the action of the projective metaplectic representation. Many geometric and numerical studies of lattices in ![]() distinguish the hexagonal lattice as being special, but this is not the case in the context of the projection functional PF and its limit value BF.
distinguish the hexagonal lattice as being special, but this is not the case in the context of the projection functional PF and its limit value BF.
In our first result we describe the invariance properties of PF and BF with respect to the projective metaplectic representation. Although the invariance of PF is standard we include it as well for the sake of completeness.
Theorem 1.1. Let μ be the projective metaplectic representation of ![]() acting on
acting on![]() . Let
. Let ![]() be a generating function of a tight Gabor frame
be a generating function of a tight Gabor frame ![]() satisfying condition Φ with respect to Λ. Then for any
satisfying condition Φ with respect to Λ. Then for any
![]()
![]() is a lattice,
is a lattice, ![]() is a tight Gabor frame with the generating function
is a tight Gabor frame with the generating function
![]() satisfying condition Φ with respect to Γ, and
satisfying condition Φ with respect to Γ, and
1) for a Gabor multiplier ![]() of localization type with the symbol bounded above by 1,
of localization type with the symbol bounded above by 1, ![]() is a Gabor multiplier of localization type with the symbol bounded above by 1, and
is a Gabor multiplier of localization type with the symbol bounded above by 1, and
![]() (5)
(5)
2) for any Ω a Λ domain, ![]() is a Γ domain, and
is a Γ domain, and
![]() (6)
(6)
Our second result is the principal result of the current paper. It describes the limit behavior of the projection functional PF applied to a Gabor multiplier with the symbol of the form![]() , i.e. the characteristic function of a dilated lattice domain Ω by a factor
, i.e. the characteristic function of a dilated lattice domain Ω by a factor![]() , with
, with![]() . Gabor multipliers of this special form are called Gabor localization operators and they are denoted as
. Gabor multipliers of this special form are called Gabor localization operators and they are denoted as![]() . We will see later on that the dilation factor R can in fact take any real values.
. We will see later on that the dilation factor R can in fact take any real values.
Theorem 1.2. Let ![]() be a generating function of a tight Gabor frame parametrized by lattice Λ and satisfying condition Φ, and Ω a Λ domain contained in
be a generating function of a tight Gabor frame parametrized by lattice Λ and satisfying condition Φ, and Ω a Λ domain contained in![]() . Then
. Then
![]() (7)
(7)
Formula (7) expresses the limit behavior of the projection functional PF in terms of the boundary form BF. It provides a very explicit, quantitative way of describing the interactions between the boundary ![]() and the reproducing kernel obtained out of the generating function
and the reproducing kernel obtained out of the generating function![]() .
.
The invariance of the projection functional PF and the boundary form BF with respect to the action of the projective metaplectic representation expressed in Theorem 1.1, taken together with the limit result of Theorem 1.2, has its important consequences. We can conclude that no lattice Λ is distinguished, neither from the point of view the value of the limit of ![]() as
as![]() , nor from the point of view of its rate of convergence.
, nor from the point of view of its rate of convergence.
Corollary 1.3. For any lattice ![]() satisfying condition
satisfying condition![]() , any generating function
, any generating function ![]() of a tight Gabor frame
of a tight Gabor frame![]() , any Λ lattice domain Ω, and any a, b > 0 satisfying
, any Λ lattice domain Ω, and any a, b > 0 satisfying![]() , there are a generating function
, there are a generating function ![]() of a tight Gabor frame
of a tight Gabor frame ![]() and a
and a ![]() lattice domain
lattice domain![]() , satisfying
, satisfying
![]() ,
, ![]() ,
, ![]() , for all R > 0, and also
, for all R > 0, and also ![]() . The rates of convergence of
. The rates of convergence of ![]() to
to![]() , and
, and ![]() to
to ![]() are the same.
are the same.
Theorem 1.2, Corollary 1.3 and part 2) of Theorem 1.1, together with their proofs, constitute new contributions of the authors to the topic of Gabor multipliers. Proofs of these results make an essential use of the extended metaplectic representation and the calculus of Gabor multipliers. Lemma 4.3 constitutes the essence of the computational setup dealing with discrete line segments. Lemmas 4.6, 4.7 deal with the reduction process of general lattice domains to unbounded strip domains. They allow the splitting of the boundary of the domain into its line segment components and the manipulation of their positions in the coordinate system.
Many important mathematical theories started in the one-dimensional setup, where a multitude of additional tools is available, and then through various stages of evolution came up into their full form in any finite dimension. This was the case of the representation theory of semi-simple Lie groups, which started with the listing of all irreducible representations of![]() . Classical TF-localization operators allow explicit diagonalization in one dimension, but not in higher dimensions, yet it was possible to transfer a large portion of one-dimensional results to higher dimensions. In one dimension, for several classes of potentials, Schrödinger operators can be treated via explicit formulae, yet many results that follow the guidelines of the one dimensional setup are also true in higher dimensions, although explicit formulae are no longer available. The development of the theory of Gabor frames follows a similar path. As this is the case of many relatively recent theories, some of its branches are still at an early, one-dimensional stage, e.g. the treatment of Gabor frames with maximal lattice parameter frame set via totally positive functions of finite type done recently by Gröchenig and Stöckler in [1] . In many instances the distinction between one and higher dimensions is related to the differences between the theories of one and several complex variables. The development of the phase space theory of reproducing formulae shows many similarities with the development of the theory of Gabor frames. The semidirect product
. Classical TF-localization operators allow explicit diagonalization in one dimension, but not in higher dimensions, yet it was possible to transfer a large portion of one-dimensional results to higher dimensions. In one dimension, for several classes of potentials, Schrödinger operators can be treated via explicit formulae, yet many results that follow the guidelines of the one dimensional setup are also true in higher dimensions, although explicit formulae are no longer available. The development of the theory of Gabor frames follows a similar path. As this is the case of many relatively recent theories, some of its branches are still at an early, one-dimensional stage, e.g. the treatment of Gabor frames with maximal lattice parameter frame set via totally positive functions of finite type done recently by Gröchenig and Stöckler in [1] . In many instances the distinction between one and higher dimensions is related to the differences between the theories of one and several complex variables. The development of the phase space theory of reproducing formulae shows many similarities with the development of the theory of Gabor frames. The semidirect product![]() , where
, where ![]() is the symplectic group consisting of
is the symplectic group consisting of ![]() invertible matrices preserving the symplectic form, together with the extended projective metaplectic representation defined on it, constitutes the group of affine transformations of the phase space, acting geometrically on
invertible matrices preserving the symplectic form, together with the extended projective metaplectic representation defined on it, constitutes the group of affine transformations of the phase space, acting geometrically on![]() , and analytically on
, and analytically on![]() . The affine transformations of the phase space provide a natural framework for the constructions of reproducing formulae. All reproducing formulae coming out of connected Lie subgroups of
. The affine transformations of the phase space provide a natural framework for the constructions of reproducing formulae. All reproducing formulae coming out of connected Lie subgroups of ![]() were characterized by De Mari and Nowak for
were characterized by De Mari and Nowak for ![]() in [2] , but no analogous results are known in higher dimensions. In dimension one
in [2] , but no analogous results are known in higher dimensions. In dimension one ![]() and it is possible to obtain the list of all connected Lie subgroups of
and it is possible to obtain the list of all connected Lie subgroups of ![]() out of the classical structure results describing the orbits of inner automorphisms of
out of the classical structure results describing the orbits of inner automorphisms of![]() . No analogous lists of subgroups are available in higher dimensions. In the current paper we deal with tight Gabor frames parametrized by a lattice
. No analogous lists of subgroups are available in higher dimensions. In the current paper we deal with tight Gabor frames parametrized by a lattice![]() . Any tight Gabor frame parameterized by a lattice
. Any tight Gabor frame parameterized by a lattice ![]() can be transferred into a tight Gabor frame parameterized by a separable lattice
can be transferred into a tight Gabor frame parameterized by a separable lattice![]() ,
, ![]() , by an appropriate
, by an appropriate ![]() linear transformation of the TF-plane. We treat the case of a separable lattice via an explicit computation and then we transfer the formula we obtain to an arbitrary lattice with the help of the projective metaplectic representation. This approach does not generalize to higher dimensions.
linear transformation of the TF-plane. We treat the case of a separable lattice via an explicit computation and then we transfer the formula we obtain to an arbitrary lattice with the help of the projective metaplectic representation. This approach does not generalize to higher dimensions.
The principal results of the current paper deal with discrete one-dimensional setup of tight Gabor frames, therefore for the sake of consistency we formulate definitions and reference results only in one dimension. Operators of composition of convolution with g followed by a pointwise multiplication by f, where both functions f and g are defined on the real line![]() , have integral kernels of the form
, have integral kernels of the form
![]() (8)
(8)
They are commonly called convolution-product operators. Historically three dimensional convolution-product operators played an important role in the study of Schrödinger operators. The Birman-Schwinger principle allows a transition from a Schrödinger operator to a convolution-product operator. Out of that transition it was possible to obtain sharp estimates for the number of bound states of the Schrödinger operator. Classical TF-lo- calization operators are one dimensional convolution-product operators with f and ǧ characteristic functions of intervals, where ǧ is the inverse Fourier transform of g. Their spectral properties were carefully studied many years ago by Landau, Pollak, Slepian and Widom (see [3] -[5] , and the references provided within), yet till now these classical results bring important ingredients for both theoretical and applied components occurring in many recent developments. There were also extensive studies of convolution-product operators with one of the function parameters f or g fixed and of prescribed potential type (see the book by Mazya [6] ), but the dependence on both parameters, and the mutual interaction between f and g in the general case seems to be a difficult problem that is to a large degree still open.
We are interested in operators with integral kernels of the form (8), where translations constituting the convolution with g are extended to combined actions of translations and modulations of the Schrödinger representation, and applied to a function![]() . As a consequence of this extension we need to introduce two arguments of the multiplier f, one corresponding to translations, the other to modulations, and the extended integral kernel (8) becomes
. As a consequence of this extension we need to introduce two arguments of the multiplier f, one corresponding to translations, the other to modulations, and the extended integral kernel (8) becomes
![]() (9)
(9)
where![]() . We add complex conjugate over
. We add complex conjugate over![]() , because we want our operators to be exactly square roots of Gabor-Toeplitz operators. The Gabor reproducing formula has the form
, because we want our operators to be exactly square roots of Gabor-Toeplitz operators. The Gabor reproducing formula has the form
![]() (10)
(10)
where![]() ,
, ![]() , and the convergence of the integral is understood in the weak sense. Introducing into (10) a weight function
, and the convergence of the integral is understood in the weak sense. Introducing into (10) a weight function![]() , called a symbol we obtain a Gabor-Toeplitz operator
, called a symbol we obtain a Gabor-Toeplitz operator
![]() (11)
(11)
Gabor-Toeplitz operators generalize Fock space Toeplitz operators. The Bargmann transform provides their mutual unitary equivalence, in case the normalized Gaussian is chosen for the generating function. Books by Folland [7] and Zhu [8] are very good references on the subject. In the field of phase space analysis Gabor- Toeplitz operators were introduced by Ingrid Daubechies. Her book [3] provides a comprehensive account of the background and the initial results. It is possible to study Gabor-Toeplitz operators in a very general context, with various classes of symbols and acting on a wide range of function spaces. It is convenient to discuss Gabor multipliers and Gabor-Toeplitz operators in parallel. In this paper we restrict attention to Gabor-Toeplitz operators of localization type acting on![]() , i.e. we assume that the symbol b is non-negative, bounded and integrable with respect to the Lebesgue measure on
, i.e. we assume that the symbol b is non-negative, bounded and integrable with respect to the Lebesgue measure on![]() . It is straightforward to verify that under these assumptions
. It is straightforward to verify that under these assumptions ![]() is non-negative, trace class,
is non-negative, trace class, ![]() the operator norm of
the operator norm of ![]() satisfies
satisfies
![]()
and that if![]() , then the composition of the operator defined by the integral kernel (9) with its conjugate equals
, then the composition of the operator defined by the integral kernel (9) with its conjugate equals ![]() defined in (11). Kernels of the form (9) represent square roots of Gabor-Toeplitz operators (11). They provide a link between Gabor-Toeplitz operators and generalized convolution-product operators, where translations are substituted by actions of unitary representations.
defined in (11). Kernels of the form (9) represent square roots of Gabor-Toeplitz operators (11). They provide a link between Gabor-Toeplitz operators and generalized convolution-product operators, where translations are substituted by actions of unitary representations.
Asymptotic properties, as![]() , of the symbolic calculus of Gabor-Toeplitz operators
, of the symbolic calculus of Gabor-Toeplitz operators![]() , where b is
, where b is
integrable, ![]() , and
, and ![]() is the
is the ![]() normalized dilation of b, were studied in [9] . For h a continuous function defined on the closed interval
normalized dilation of b, were studied in [9] . For h a continuous function defined on the closed interval ![]() the operator
the operator ![]() is defined via the spec-
is defined via the spec-
tral decomposition of![]() . A Szegö type formula for operators of the form
. A Szegö type formula for operators of the form ![]() was obtained in [9] , showing that
was obtained in [9] , showing that
![]() (12)
(12)
We need to multiply ![]() by
by ![]() in formula (12) in order to ensure that the operator is trace class. The Bohr correspondence principle was concluded as a consequence of (12). It asserts that in the normalized limit with factor
in formula (12) in order to ensure that the operator is trace class. The Bohr correspondence principle was concluded as a consequence of (12). It asserts that in the normalized limit with factor ![]() in the denominator both the distribution of the eigenvalues of
in the denominator both the distribution of the eigenvalues of ![]()
![]() (13)
(13)
and the size of their plunge region
![]() (14)
(14)
are expressed directly via the corresponding quantities of the symbol function, the distribution of b
![]() (15)
(15)
and the Lebesgue measure of its plunge region
![]() (16)
(16)
In the passage to the normalized limit it is necessary to assume that the level sets![]() ,
, ![]() , have Lebesgue measure 0. We were able to deduce that asymptotically the best localization properties, i.e. asymptotically there are no eigenvalues in the open interval
, have Lebesgue measure 0. We were able to deduce that asymptotically the best localization properties, i.e. asymptotically there are no eigenvalues in the open interval![]() , occur for symbols being characteristic functions of measurable sets
, occur for symbols being characteristic functions of measurable sets![]() .
.
In the next step operators![]() , with symbols
, with symbols![]() , were studied directly without the asymptotic limit. Two-sided estimates of the size of the eigenvalue plunge region
, were studied directly without the asymptotic limit. Two-sided estimates of the size of the eigenvalue plunge region
![]() (17)
(17)
expressed in terms of the area of a strip of fixed size R around the boundary ![]() and uniform with respect to generating functions
and uniform with respect to generating functions ![]() and localization domains Ω, of the form
and localization domains Ω, of the form
![]() (18)
(18)
where![]() , were obtained in [10] . In order to get two-sided uniform positive constants c1, c2 it was necessary to assume uniform decay and non-degeneracy of the reproducing kernels obtained out of generating functions
, were obtained in [10] . In order to get two-sided uniform positive constants c1, c2 it was necessary to assume uniform decay and non-degeneracy of the reproducing kernels obtained out of generating functions ![]() and uniform access to localization domains Ω and their complements Ωc from the points near their boundaries
and uniform access to localization domains Ω and their complements Ωc from the points near their boundaries![]() . The size R of the strip
. The size R of the strip ![]() around
around ![]() is one of the uniform parameters controlling mutual interactions between the generating functions
is one of the uniform parameters controlling mutual interactions between the generating functions ![]() and domains of localization Ω.
and domains of localization Ω.
The next step in the study of mutual interactions between generating functions and domains of localization from the point of view of estimating the size of the eigenvalue plunge region was accomplished in [11] . The eigenvalues of Gabor-Toeplitz localization operators ![]() satisfy estimates
satisfy estimates![]() . The projection functional
. The projection functional ![]() provides an exact, quantitative way of measuring the size of the eigenvalue plunge region. It has the same form as in (3) in the discrete setup. We assume that Ω is a bounded domain with C1 boundary. Symbol
provides an exact, quantitative way of measuring the size of the eigenvalue plunge region. It has the same form as in (3) in the discrete setup. We assume that Ω is a bounded domain with C1 boundary. Symbol ![]() denotes the arc length defined on
denotes the arc length defined on![]() . Function n is the Gauss map, i.e.
. Function n is the Gauss map, i.e. ![]() is the unit normal vector at
is the unit normal vector at ![]() directed outside Ω. By
directed outside Ω. By ![]() we denote the linear subspace of
we denote the linear subspace of ![]() consisting of vectors orthogonal to v, and
consisting of vectors orthogonal to v, and ![]() is the half space inside
is the half space inside ![]() with v being the inner normal vector. The boundary form is defined as
with v being the inner normal vector. The boundary form is defined as
![]() (19)
(19)
Under an appropriate integrability condition imposed on![]() , condition Φ of the current paper is its adaptation to the discrete setup, that makes formula (19) well defined it has been shown in [11] that
, condition Φ of the current paper is its adaptation to the discrete setup, that makes formula (19) well defined it has been shown in [11] that
![]() (20)
(20)
Formula (20) expresses the limit behavior of the projection functional in terms of the boundary form. It describes quantitatively the interactions between the boundary ![]() and the reproducing kernel obtained out of the generating function
and the reproducing kernel obtained out of the generating function![]() . Boundary form (4) is an adaptation of (19) to the discrete setup.
. Boundary form (4) is an adaptation of (19) to the discrete setup.
Let us fix the area A and a generating function ![]() for which the boundary form (19) is well defined, and let us ask for what localization domains Ω of area A the boundary form
for which the boundary form (19) is well defined, and let us ask for what localization domains Ω of area A the boundary form ![]() takes the smallest possible value. Let us introduce surface tension
takes the smallest possible value. Let us introduce surface tension![]() , defined on the unit sphere of the TF-plane
, defined on the unit sphere of the TF-plane![]() , given by the formula
, given by the formula
![]() (21)
(21)
Function![]() , defined in (21), determines the Wulff shape
, defined in (21), determines the Wulff shape
![]() (22)
(22)
For the given generating function ![]() let us construct
let us construct![]() , defined in (22), and let us scale it with a constant c, so that the area of
, defined in (22), and let us scale it with a constant c, so that the area of ![]() is A. It occurs, that, up to translation, the domain
is A. It occurs, that, up to translation, the domain ![]() is the only domain among all domains Ω with finite perimeter and area A for which
is the only domain among all domains Ω with finite perimeter and area A for which ![]() is minimal. The shape
is minimal. The shape ![]() is the optimal domain of localization.
is the optimal domain of localization.
The principal results of the current paper deal with the discrete setup of tight Gabor frames defined on![]() . On the level of convolution-product operators with kernels of the form (8) the transition to the discrete setup translates to making the range variables discrete and keeping the domain variables continuous. The multiplication parameter f is now defined on the group of integers, but the convolution parameter g is still defined on the real line
. On the level of convolution-product operators with kernels of the form (8) the transition to the discrete setup translates to making the range variables discrete and keeping the domain variables continuous. The multiplication parameter f is now defined on the group of integers, but the convolution parameter g is still defined on the real line![]() . After the modification the integral kernel (8) becomes
. After the modification the integral kernel (8) becomes
![]() (23)
(23)
In the discrete setup the Gabor reproducing formula (10) is substituted by a tight Gabor frame expansion (1)
![]()
and the Gabor-Toeplitz operator (11) by a Gabor multiplier (2)
![]()
Gabor multipliers were introduced as a phase space analysis tool parallel to Gabor expansions. Both Gabor- Toeplitz operators and Gabor multipliers are currently very actively investigated, mostly from the point of view of their usage in phase space analysis. They were applied as phase space partitioning operators in [12] , leading to a new characterization of modulation spaces, as isomorphism maps, in [13] [14] , in the context of modulation spaces and weighted Bargmann-Fock spaces, in [15] -[19] as approximation blocks for the representation of Hilbert-Schmidt, pseudodifferential, and Fourier integral operators. A recent survey [20] provides an overview of the results on both Gabor-Toeplitz operators and Gabor multipliers from the point of view of phase space localization. Not all of the phenomena are the same for Gabor-Toplitz operators and Gabor multipliers. The cut-off phenomenon happens only in the continuous setup (see [21] ); the Berezin transform is invertible in a stable way only in the discrete setup (see [22] ).
We restrict attention to Gabor multipliers of localization type, i.e. we assume that the symbol b defined on Λ is non-negative and summable. The operator with kernel
![]()
a discrete analogue of (9), acting from ![]() into
into![]() , is again a square root of
, is again a square root of![]() , provided
, provided ![]() . [22] provides discrete versions of (12), (13), (14), (17).
. [22] provides discrete versions of (12), (13), (14), (17).
Out of Theorems 1.1, 1.2 we were able to conclude Corollary 1.3, expressing the fact that from the point of view of the projection functional PF and the boundary form BF no lattice Λ is distinguished. It would be interesting to isolate those phase space phenomena that make distinction between lattices parameterizing tight Gabor frames. The book by Martinet [23] is a comprehensive resource on lattices in Euclidean spaces.
In the continuous case the Wulff shape (22) is the optimal localization domain. There is no analogue of it for lattice domains. We do not know how large is the class of localization domains for which the asymptotic boundary forms exist. We expect that in the general case the problem of existence of normalized limits of projection functionals has to be considered in parallel with the asymptotic properties of the counting function ![]() as
as![]() . Harmonic analysis background on the counting problem
. Harmonic analysis background on the counting problem ![]() as
as![]() , together with the original Hlawka result, and several developments that followed afterwards are presented in Stein’s book [24] . The paper by Nowak [25] discusses more recent approaches to the topic.
, together with the original Hlawka result, and several developments that followed afterwards are presented in Stein’s book [24] . The paper by Nowak [25] discusses more recent approaches to the topic.
Books by Christensen [26] , Daubechies [3] , Flandrin [27] , Gröchenig [28] , Wojtaszczyk [29] , and collected volumes by Feichtinger, Strohmer [30] [31] present a broad background of phase space analysis techniques needed for the theory of Gabor expansions. Papers by Balan [32] , Cassaza [33] , Heil [34] illustrate several further aspects of Gabor analysis not treated directly in this paper.
2. Tight Gabor Frames, Their Constructions and Properties
Let ![]() be a Hilbert space. A family of functions
be a Hilbert space. A family of functions ![]() is called a frame of
is called a frame of ![]() if there are constants
if there are constants ![]() such that for any
such that for any ![]()
![]() (24)
(24)
For any frame of ![]() it is possible to choose the largest constant A and the smallest constant B for which (24) holds. These two extreme values of A and B are called the lower and the upper frame bounds of the frame
it is possible to choose the largest constant A and the smallest constant B for which (24) holds. These two extreme values of A and B are called the lower and the upper frame bounds of the frame![]() . If the lower and the upper frame bounds are equal then the frame is called tight. Any tight frame gives
. If the lower and the upper frame bounds are equal then the frame is called tight. Any tight frame gives
rise to a discrete reproducing formula. We may renormalize a tight frame ![]() and obtain the norm equality
and obtain the norm equality
![]() which in turn via the polarization identity may be interpreted as a reproducing formula
which in turn via the polarization identity may be interpreted as a reproducing formula
![]() (25)
(25)
with the convergence of the sum understood in the unconditional norm sense. There is a canonical way of constructing a tight frame out of a frame. For any frame ![]() we define a frame operator via
we define a frame operator via
![]() (26)
(26)
Condition (24) guarantees that the above sum is unconditionally convergent for any ![]() and that the linear operator S defined in (26) is positive definite, bounded and invertible on
and that the linear operator S defined in (26) is positive definite, bounded and invertible on![]() . It is straightforward to verify that the family
. It is straightforward to verify that the family ![]() is a tight frame on
is a tight frame on![]() .
.
Gabor frames have the form![]() , where
, where![]() ,
, ![]() , and
, and ![]() is a lattice in
is a lattice in
![]() . We assume that the system
. We assume that the system ![]() is a tight Gabor frame normalized in such a way that the reproducing formula (25) holds.
is a tight Gabor frame normalized in such a way that the reproducing formula (25) holds.
Let![]() ,
, ![]() , be a weight function defined on
, be a weight function defined on ![]() by the formula
by the formula
![]() (27)
(27)
Let ![]() denote the space of Schwartz class functions and
denote the space of Schwartz class functions and ![]() the space of tempered distributions. Let us select a non-zero function
the space of tempered distributions. Let us select a non-zero function ![]() and define the modulation space
and define the modulation space![]() ,
, ![]() , as the space consisting of those tempered distributions
, as the space consisting of those tempered distributions ![]() for which the norm
for which the norm
![]() (28)
(28)
is finite. If ![]() or
or ![]() the integral norm is substituted by the essential supremum. The definition of the modulation space does not depend on the choice of function g. For different functions g the corresponding norms are equivalent. If
the integral norm is substituted by the essential supremum. The definition of the modulation space does not depend on the choice of function g. For different functions g the corresponding norms are equivalent. If ![]() we write
we write ![]() instead of
instead of![]() .
.
Let us recall that a function ![]() satisfies condition Φ with respect to lattice Λ if and only if
satisfies condition Φ with respect to lattice Λ if and only if ![]() . Condition Φ is necessary and sufficient for the boundary form
. Condition Φ is necessary and sufficient for the boundary form ![]() of formula (4) to be well defined for any Λ lattice domain Ω. The next proposition formulates a sufficient condition on a function
of formula (4) to be well defined for any Λ lattice domain Ω. The next proposition formulates a sufficient condition on a function![]() , expressed in terms of modulation spaces, for condition Φ to hold. Our sufficient condition follows by a direct application of the Young’s inequality and the standard theory of modulation spaces presented in [28] . We do not include its proof.
, expressed in terms of modulation spaces, for condition Φ to hold. Our sufficient condition follows by a direct application of the Young’s inequality and the standard theory of modulation spaces presented in [28] . We do not include its proof.
Proposition 2.1. If![]() , then
, then ![]() satisfies condition Φ.
satisfies condition Φ.
The first construction of tight Gabor frames in dimension 1 was obtained by Daubechies, Grossmann and Meyer in 1986. Tight Gabor frames were called painless nonortho-gonal expansions back then. The construction produced generating functions with compact support either in position or in momentum and with arbitrary smoothness measured by the number of continuous derivatives, any ![]() or
or ![]() was possible. The book by Daubechies [3] provides an excellent account of the initial stages of the constructions of tight Gabor frames. Then came Wexler-Raz biorthogonality relations, Walnut, Janssen representations, and Ron-Shen duality principle dealing with Gabor frames and the frame operator in any finite dimension. All these are very nicely presented in Gröchenig’s book [28] . Tight Gabor frames and in particular canonical tight Gabor frames obtained via the action of
was possible. The book by Daubechies [3] provides an excellent account of the initial stages of the constructions of tight Gabor frames. Then came Wexler-Raz biorthogonality relations, Walnut, Janssen representations, and Ron-Shen duality principle dealing with Gabor frames and the frame operator in any finite dimension. All these are very nicely presented in Gröchenig’s book [28] . Tight Gabor frames and in particular canonical tight Gabor frames obtained via the action of![]() , where S is the frame operator, are of the principal interest from the point of view of this paper. Generating functions being members of the modulation space
, where S is the frame operator, are of the principal interest from the point of view of this paper. Generating functions being members of the modulation space![]() , where W is a subexponential weight, are the building blocks for all other modulation spaces. Subexponential weights are a natural generalization of the standard weights
, where W is a subexponential weight, are the building blocks for all other modulation spaces. Subexponential weights are a natural generalization of the standard weights ![]() defined in (27) (see [35] for the definition, provided on page 10, and for explanations of their usage in TF-analysis). It is important to know how to construct generating functions of tight Gabor frames, which are members of
defined in (27) (see [35] for the definition, provided on page 10, and for explanations of their usage in TF-analysis). It is important to know how to construct generating functions of tight Gabor frames, which are members of![]() . The major result in this direction was obtained by Gröchenig and Leinert in [35] , where they proved that, for any lattice
. The major result in this direction was obtained by Gröchenig and Leinert in [35] , where they proved that, for any lattice![]() , the canonical tight frame operator
, the canonical tight frame operator ![]() is bounded on
is bounded on![]() . If we have a Gabor frame with the generating function in
. If we have a Gabor frame with the generating function in![]() , then we also have a tight Gabor frame with the generating function in
, then we also have a tight Gabor frame with the generating function in![]() . The existence of a generating function in
. The existence of a generating function in ![]() of a Gabor frame, for any lattice
of a Gabor frame, for any lattice![]() , with the volume of the fundamental domain satisfying
, with the volume of the fundamental domain satisfying![]() , was established recently by Luef [36] . Feichtinger and Kaiblinger examined, from the point of view modulation spaces, continuity properties of the canonical dual generating function, i.e.
, was established recently by Luef [36] . Feichtinger and Kaiblinger examined, from the point of view modulation spaces, continuity properties of the canonical dual generating function, i.e.![]() , where
, where ![]() is the frame operator, with respect to the perturbations of the lattice. They proved in [37] that the set
is the frame operator, with respect to the perturbations of the lattice. They proved in [37] that the set
![]() is open and that the map
is open and that the map ![]() is conti-
is conti-
nuous from ![]() into
into![]() . Leinert and Luef show a similar result for the canonical tight atoms
. Leinert and Luef show a similar result for the canonical tight atoms ![]() [36] .
[36] .
3. Proofs of the Main Results
We start by recalling the definitions of our principal objects of interest. We assume that a tight Gabor frame ![]() is given, indexed by a lattice
is given, indexed by a lattice![]() , normalized so that the reproducing formula (1) holds. A Gabor multiplier of localization type (2) is constructed out of the reproducing system
, normalized so that the reproducing formula (1) holds. A Gabor multiplier of localization type (2) is constructed out of the reproducing system![]() , and a non-negative, summable, and bounded above by 1 symbol b, defined on Λ. It is defined by the formula
, and a non-negative, summable, and bounded above by 1 symbol b, defined on Λ. It is defined by the formula ![]() The projection functional (3) applied to
The projection functional (3) applied to ![]() has the form
has the form
![]()
where ![]() are the eigenvalues of
are the eigenvalues of![]() . Condition Φ, the additional requirement imposed on the ge-
. Condition Φ, the additional requirement imposed on the ge-
nerating function![]() ,
, ![]() , is a necessary and a sufficient condition for the boundary form (4) to be well defined for any Λ localization domain Ω,
, is a necessary and a sufficient condition for the boundary form (4) to be well defined for any Λ localization domain Ω,
![]()
where![]() ,
, ![]() are the line segments constituting the boundary of Ω,
are the line segments constituting the boundary of Ω, ![]() is the unit vector orthogonal to
is the unit vector orthogonal to ![]() directed outside Ω,
directed outside Ω, ![]() ,
,![]() .
.
Now we are ready to present the proof of Theorem 1.1.
Theorem 1.1. Let ![]() be the projective metaplectic representation of
be the projective metaplectic representation of ![]() acting on
acting on![]() . Let
. Let ![]() be a generating function of a tight Gabor frame
be a generating function of a tight Gabor frame ![]() satisfying condition Φ with respect to Λ. Then for any
satisfying condition Φ with respect to Λ. Then for any
![]()
![]() is a lattice,
is a lattice, ![]() is a tight Gabor frame with the generating function
is a tight Gabor frame with the generating function ![]() satisfying condition Φ with respect to Γ, and
satisfying condition Φ with respect to Γ, and
1) for any Gabor multiplier ![]() of localization type with the symbol bounded above by 1,
of localization type with the symbol bounded above by 1, ![]() is a Gabor multiplier of localization type with the symbol bounded above by 1, and
is a Gabor multiplier of localization type with the symbol bounded above by 1, and
![]()
2) for any Ω a Λ domain, ![]() is a Γ domain, and
is a Γ domain, and
![]()
Proof. The transformation rule 2) of Lemma 4.1, describing the effect of the conjugation by the projective metalplectic representation, shows that 1), i.e. formula (5) holds.
In the remaining part of the proof we deal with 2), i.e. with formula (6)
![]()
The group ![]() acts transitively on the collection of all lattices
acts transitively on the collection of all lattices ![]() satisfying condition
satisfying condition![]() . Therefore, we may assume that
. Therefore, we may assume that![]() , where
, where ![]() and
and![]() . It is clear that for any
. It is clear that for any ![]()
![]() is an
is an ![]() domain. The proof of the BF invariance rule (6), describing the transition from Λ to
domain. The proof of the BF invariance rule (6), describing the transition from Λ to ![]() via A, requires two ingredients, the transformation rule for the reproducing kernel
via A, requires two ingredients, the transformation rule for the reproducing kernel
![]() (29)
(29)
and for the geometric atoms
![]() (30)
(30)
where![]() , s is a line segment with its endpoints being the points of lattice Λ, constituting a portion of the boundary of Ω, l is the line parallel to s, and passing through
, s is a line segment with its endpoints being the points of lattice Λ, constituting a portion of the boundary of Ω, l is the line parallel to s, and passing through![]() . These two, (29) and (30), constitute the basic building blocks of the boundary form. Lemma 4.1 1) provides the formula describing the transformation of the reproducing kernel (29) under the action of the projective metaplectic representation, it is enough to apply it. However, we need to deal with the geometric atoms (30), via a direct computation.
. These two, (29) and (30), constitute the basic building blocks of the boundary form. Lemma 4.1 1) provides the formula describing the transformation of the reproducing kernel (29) under the action of the projective metaplectic representation, it is enough to apply it. However, we need to deal with the geometric atoms (30), via a direct computation.
The linear map ![]() providing the transition from Λ to
providing the transition from Λ to ![]() satisfies condition
satisfies condition![]() , therefore it preserves the orientation of the boundary. It transforms a line segment
, therefore it preserves the orientation of the boundary. It transforms a line segment ![]() of the boundary of Ω to the corresponding line segment
of the boundary of Ω to the corresponding line segment ![]() of
of![]() , and the half lattice
, and the half lattice ![]() of Λ to the corresponding half lattice
of Λ to the corresponding half lattice ![]() of
of![]() . The fact that A might not preserve orthogonality does not matter. Lemma 4.1 1) allows us to conclude that the transformation of the boundary form BF is correct as far as the reproducing kernel (29) is concerned. It also shows that condition Φ transforms properly. We need to show that the geometric atoms
. The fact that A might not preserve orthogonality does not matter. Lemma 4.1 1) allows us to conclude that the transformation of the boundary form BF is correct as far as the reproducing kernel (29) is concerned. It also shows that condition Φ transforms properly. We need to show that the geometric atoms ![]() of (30) also transform properly, i.e. that
of (30) also transform properly, i.e. that
![]() (31)
(31)
where![]() . Figure 1 illustrates the right hand side of formula (34).
. Figure 1 illustrates the right hand side of formula (34).
The Iwasawa decomposition of ![]() (see [38] ) allows us to represent A as PK, where P is upper triangular and K is a rotation matrix, both in
(see [38] ) allows us to represent A as PK, where P is upper triangular and K is a rotation matrix, both in![]() . Since K is unitary it preserves distances and angles. It is clear that the geometric atoms properly transform under K. It is therefore enough to consider the upper triangular P. In order to show that (31) holds, we consider R, the inverse of P, providing a transition from
. Since K is unitary it preserves distances and angles. It is clear that the geometric atoms properly transform under K. It is therefore enough to consider the upper triangular P. In order to show that (31) holds, we consider R, the inverse of P, providing a transition from ![]() to Λ. We verify that
to Λ. We verify that
![]() (32)
(32)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() is the line segment connecting points
is the line segment connecting points ![]() and
and![]() ,
,
![]() is the line containing
is the line containing![]() , and
, and![]() . Translation invariance of the Euclidean length allows us to assume that the line segment under consideration, constituting a portion of the boundary of the domain of localization Ω, starts at the origin
. Translation invariance of the Euclidean length allows us to assume that the line segment under consideration, constituting a portion of the boundary of the domain of localization Ω, starts at the origin![]() .
.
![]()
Figure 1. Displays the components of geometric atoms.
We observe that![]() ,
,
![]()
the normalized vector v orthogonal to ![]() equals
equals
![]()
therefore we obtain
![]()
The above calculation verifies (32). It also shows (31), since plugging![]() , i.e. taking
, i.e. taking![]() ,
, ![]() produces the geometric atom on
produces the geometric atom on![]() .
.
Let us recall that Gabor multipliers with symbols of the form ![]() are called Gabor localization operators and that they are denoted
are called Gabor localization operators and that they are denoted![]() . The proof of Theorem 1.2, the principal result of the current paper, is very lengthy and it makes use of all the auxiliary facts collected in Section 4. In order to facilitate the reading, we list the steps of the proof first, and then we present their proofs.
. The proof of Theorem 1.2, the principal result of the current paper, is very lengthy and it makes use of all the auxiliary facts collected in Section 4. In order to facilitate the reading, we list the steps of the proof first, and then we present their proofs.
Theorem 1.2. Let ![]() be a generating function of a tight Gabor frame parametrized by lattice Λ and satisfying condition Φ, and Ω a Λ domain contained in
be a generating function of a tight Gabor frame parametrized by lattice Λ and satisfying condition Φ, and Ω a Λ domain contained in![]() . Then
. Then
![]()
Steps of Proof:
Step 1. We make a transition from lattice Λ to![]() , where the computation is easier to handle. We construct a matrix
, where the computation is easier to handle. We construct a matrix ![]() and scaling parameters
and scaling parameters![]() , such that
, such that ![]() and
and![]() , where
, where ![]() is the scaling matrix with numbers a, b on its diagonal and zeros elsewhere. We will work with the
is the scaling matrix with numbers a, b on its diagonal and zeros elsewhere. We will work with the ![]() domain
domain ![]() instead of the Λ domain Ω and with the generating function
instead of the Λ domain Ω and with the generating function ![]() of the tight Gabor frame
of the tight Gabor frame
![]() instead of the generating function
instead of the generating function ![]() of the tight Gabor frame
of the tight Gabor frame![]() . Symbol
. Symbol ![]() de-
de-
notes the projective metaplectic representation defined on![]() . We substitute the Gabor multiplier
. We substitute the Gabor multiplier ![]() by the operator
by the operator![]() , which is unitary equivalent to it, and defined by the formula
, which is unitary equivalent to it, and defined by the formula
![]() (33)
(33)
Once the unitary equivalence is verified it is clear that
![]() (34)
(34)
We substitute the boundary form ![]() defined in (4) by the boundary form
defined in (4) by the boundary form ![]() defined in terms of the
defined in terms of the ![]() domain
domain ![]() and the image of the original generating function
and the image of the original generating function ![]() of the tight Gabor frame
of the tight Gabor frame ![]() under
under![]() ,
,
![]() (35)
(35)
where li, ![]() are the line segments constituting the boundary of
are the line segments constituting the boundary of![]() , ni is the unit vector or-
, ni is the unit vector or-
thogonal to li directed outside![]() ,
, ![]() ,
,![]() . We show that in view of condition Φ the form (35) is well defined and that
. We show that in view of condition Φ the form (35) is well defined and that
![]() (36)
(36)
Step 2. We use tight Gabor frames versions of Toeplitz and Hankel operators in order to express the projection functional
![]()
as the square of the Hilbert-Schmidt norm of the matrix
![]() (37)
(37)
where![]() . As the result we obtain the equality
. As the result we obtain the equality
![]() (38)
(38)
where
![]() (39)
(39)
Next, we change variables and let them range over the dilated lattice![]() . The right hand side of (38) becomes
. The right hand side of (38) becomes
![]() (40)
(40)
Step 3. We split the boundary of ![]() into its component lattice cycles, then into their individual line segments, and then we reduce the computation of the limit to the sum of the limits over the line segments constituting the boundary. We may assume that each boundary segment connects lattice points and does not have lattice points in its interior. If necessary we divide it into subsegments. Each sufficiently small neighborhood of a boundary segment gets represented as an unbounded vertical strip domain, for which expression (40) becomes
into its component lattice cycles, then into their individual line segments, and then we reduce the computation of the limit to the sum of the limits over the line segments constituting the boundary. We may assume that each boundary segment connects lattice points and does not have lattice points in its interior. If necessary we divide it into subsegments. Each sufficiently small neighborhood of a boundary segment gets represented as an unbounded vertical strip domain, for which expression (40) becomes
![]() (41)
(41)
and function H representing a given segment of the boundary is a linear function with rational slope of the form![]() , with
, with![]() ,
, ![]() ,
, ![]() , and m, n relatively prime. The graph of H constitutes the top portion of the boundary of the unbounded vertical strip domain
, and m, n relatively prime. The graph of H constitutes the top portion of the boundary of the unbounded vertical strip domain![]() . Points
. Points ![]() satisfying condition
satisfying condition ![]() lie above the graph of H, and points
lie above the graph of H, and points ![]() for which
for which ![]() are located below or on the graph of H. Function F is obtained out of
are located below or on the graph of H. Function F is obtained out of ![]() via a lattice transformation of Lemma 4.5 that brings the selected fragment of the boundary to the form described above.
via a lattice transformation of Lemma 4.5 that brings the selected fragment of the boundary to the form described above.
Step 4. We adjust the form of variables x1, x2 to the arithmetic form of the slope of H. We represent x1, x2 as![]() ,
, ![]() , where k1, k2 are integers and
, where k1, k2 are integers and![]() . With new variables k1, r1, k2, r2, expression (41) becomes
. With new variables k1, r1, k2, r2, expression (41) becomes
![]() (42)
(42)
Step 5. Invariance of expression (42) with respect to variables y1, y2 allows us to substitute the double summation with a single summation. We count the number of repetitions in the representation ![]() and we place an appropriate factor that compensates them. Expression (42) becomes
and we place an appropriate factor that compensates them. Expression (42) becomes
![]() (43)
(43)
where square brackets denote the integer part of a rational number.
Step 6. Form (43) is convenient for making the passage to the limit. It occurs that taking the limit in (43) with respect to R is just the same as performing summation with respect to k. We obtain
![]() (44)
(44)
Step 7. We write expression (44) in the form involving function ![]()
![]() (45)
(45)
where
![]() (46)
(46)
Step 8. We interpret expression (45) geometrically. We make use of the structural features of lattice lines and we show that in fact (45) equals
![]() (47)
(47)
where ![]() is the graph of H, U is the part of
is the graph of H, U is the part of ![]() lying above G and dist is the Euclidean
lying above G and dist is the Euclidean
distance inside the plane ![]() containing lattice
containing lattice![]() . Constant
. Constant ![]() represents the contribution of vertic-
represents the contribution of vertic-
al strip domain ![]() to the total length of the boundary of
to the total length of the boundary of![]() .
.
Step 9. We put together the boundary forms (47) of vertical strip domains corresponding to all line segments of the boundary of ![]() and we obtain
and we obtain
![]() (48)
(48)
In view of (34), and (36), formula (48) concludes the proof.
Proofs of Steps:
Proof of Step 1. We construct matrix![]() , satisfying property
, satisfying property![]() , a, b > 0,
, a, b > 0, ![]() , by assigning values
, by assigning values![]() ,
, ![]() to the generators of Λ and then extending the assignment by linearity. The inverse of the scaling matrix
to the generators of Λ and then extending the assignment by linearity. The inverse of the scaling matrix ![]() provides a transition from
provides a transition from ![]() to
to![]() ,
,![]() . Matrices A and
. Matrices A and ![]() are the arithmetic tools needed for the transition from Λ to
are the arithmetic tools needed for the transition from Λ to![]() . The unitary operator
. The unitary operator![]() , where
, where ![]() is the projective metaplectic representation defined on
is the projective metaplectic representation defined on![]() , is the analytic tool responsible for the transition needed on the level of the generating functions of tight Gabor frames. We observe that in view of Lemma 4.1 2) and definition (33) of
, is the analytic tool responsible for the transition needed on the level of the generating functions of tight Gabor frames. We observe that in view of Lemma 4.1 2) and definition (33) of ![]()
![]()
We conclude that (34) holds. The transition from Λ to ![]() is justified as far the operator properties, i.e. the values of the projection functional, are concerned.
is justified as far the operator properties, i.e. the values of the projection functional, are concerned.
The justification of the transition from Λ to ![]() as far as the geometric properties, i.e. the boundary form, are concerned, follows from Theorem 1.1 2). We obtain
as far as the geometric properties, i.e. the boundary form, are concerned, follows from Theorem 1.1 2). We obtain
![]()
but we still need to switch to ![]() defined in (35). In order to do that, we observe that the boundary form scales with respect to the action of
defined in (35). In order to do that, we observe that the boundary form scales with respect to the action of ![]() via the area factor ab, and this allows us to finish the proof of (36)
via the area factor ab, and this allows us to finish the proof of (36)
![]()
Proof of Step 2. Since
![]()
Lemma 4.2 implies that
![]()
where ![]() is defined in (37).
is defined in (37).
Proof of Step 3. This is the most tedious step of the proof. For the sake of notational convenience we will use symbol ![]() for the current domain under consideration. It will be clear from the context what it is at a given stage of the proof. Initially
for the current domain under consideration. It will be clear from the context what it is at a given stage of the proof. Initially ![]() denotes
denotes![]() . Figure 2 explains the process of traversing the boundary
. Figure 2 explains the process of traversing the boundary![]() . Our first target is to cut the kernel
. Our first target is to cut the kernel
![]()
into pieces with the help of a partition of unity of ![]() obtained out of quadrilaterals formed around the boundary segments constituting
obtained out of quadrilaterals formed around the boundary segments constituting ![]() and two open sets isolated from the boundary and representing the exterior and the interior of Ω.
and two open sets isolated from the boundary and representing the exterior and the interior of Ω.
We traverse each component of the boundary of Ω according to the orientation, keeping the interior on the right and the exterior on the left, and at each initial lattice point of the boundary segment li we place a sufficiently small rational line segment si with its middle being the initial lattice point. We chose si in such a way that it is transversal to both li and the boundary segment ll preceding it, and that both exterior and interior angles with li and ll are smaller than π. We assume that segments si, i = 1, ∙∙∙, N are so small so that they intersect the boundary ![]() exactly at one point. We assume that they are positioned in such a way that one of the endpoints of si is inside the interior of Ω and the other in the exterior of Ω. Let lr be the segment following li. We form quadrilaterals Wi out of consecutive segments si, sr attached at the beginning and at the end of li, and the segments joining their endpoints, both endpoints inside the interior of Ω or both in the exterior of Ω. Figure 3 illustrates the construction of quadrilaterals Wi. We also assume that the sizes of the transversal segments are so small so that the segments joining the endpoints of si and sr are contained either in the exterior or in the interior of Ω. We include si inside Wi, but not sr. Adding sr to Wi we would obtain a closed quadrilateral, but we need to form a family of pairwise disjoint sets, and sr is already included in Wr.
exactly at one point. We assume that they are positioned in such a way that one of the endpoints of si is inside the interior of Ω and the other in the exterior of Ω. Let lr be the segment following li. We form quadrilaterals Wi out of consecutive segments si, sr attached at the beginning and at the end of li, and the segments joining their endpoints, both endpoints inside the interior of Ω or both in the exterior of Ω. Figure 3 illustrates the construction of quadrilaterals Wi. We also assume that the sizes of the transversal segments are so small so that the segments joining the endpoints of si and sr are contained either in the exterior or in the interior of Ω. We include si inside Wi, but not sr. Adding sr to Wi we would obtain a closed quadrilateral, but we need to form a family of pairwise disjoint sets, and sr is already included in Wr.
![]()
Figure 2. Explains the process of traversing the boundary![]() .
.
![]()
Figure 3. Illustrates the construction of quadrilaterals![]() .
.
We define a partition of ![]() out of quadrilaterals
out of quadrilaterals ![]() forming a neighborhood of the boundary
forming a neighborhood of the boundary ![]() and two open sets
and two open sets![]() ,
, ![]() representing the exterior and the interior of Ω. Let
representing the exterior and the interior of Ω. Let![]() ,
, ![]() ,
,![]() . We define
. We define
![]()
![]()
![]()
![]()
We observe that
![]() (49)
(49)
We do not need terms with factors ![]() and
and ![]() in the above decomposition, since
in the above decomposition, since ![]() and
and![]() . We know that
. We know that![]() ,
, ![]() , therefore Lemma 4.6 allows us to conclude
, therefore Lemma 4.6 allows us to conclude
![]() (50)
(50)
for![]() . Since
. Since ![]() for
for ![]() such that
such that ![]() are not neighboring line segments, again by Lemma 4.6 we obtain
are not neighboring line segments, again by Lemma 4.6 we obtain
![]() (51)
(51)
If![]() , but
, but ![]() are neighboring line segments (Figure 4), then Lemma 4.7 applies and we conclude again
are neighboring line segments (Figure 4), then Lemma 4.7 applies and we conclude again
![]() (52)
(52)
Formula (49)-(52) allow us to conclude that only terms of the form
![]()
contribute to the limit.
Let us recall that we assumed that each boundary segment lk connects lattice points and does not have lattice points in its interior. We may apply Lemma 4.5 in order to bring each segment lk to the form![]() , with
, with
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , n, m relatively prime, with the image of Ω placed below the
, n, m relatively prime, with the image of Ω placed below the
graph of H, and the image of ![]() placed above the graph of H. Under the transformation of Lemma 4.5 quadrilateral
placed above the graph of H. Under the transformation of Lemma 4.5 quadrilateral ![]() becomes
becomes ![]() (Figure 5). With the help of Lemma 4.7 we bring
(Figure 5). With the help of Lemma 4.7 we bring ![]() to a form of a bounded vertical strip domain with the top portion of the boundary represented by a line tk and the bottom portion by a line bk. Lemma 4.6 allows us to substitute the bounded vertical strip domain we have just obtained by a rectangle with the top boundary represented by a horizontal line
to a form of a bounded vertical strip domain with the top portion of the boundary represented by a line tk and the bottom portion by a line bk. Lemma 4.6 allows us to substitute the bounded vertical strip domain we have just obtained by a rectangle with the top boundary represented by a horizontal line![]() , with
, with![]() , placed above tk, and the bottom boundary represented by a horizontal line
, placed above tk, and the bottom boundary represented by a horizontal line![]() , with
, with![]() , placed below bk.
, placed below bk.
In the last step we switch to the unbounded strip domain
![]()
with its complement
![]()
![]()
Figure 4. Explains the usage of Lemma 4.7 for neighboring segments lk, ll.
![]()
Figure 5. Illustrates the usage of quadrilateral![]() .
.
We have the splitting
![]()
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
![]() (56)
(56)
We need to show that the normalized sums coming out of terms (54), (55), (56) have zero limits. Lemma 4.6 applies to both (54), (55), but (56) needs to be treated separately. After the change of variables the normalized sum of (56) becomes
![]()
In the proof that its limit is zero as ![]() we may assume that R is an integer. Let
we may assume that R is an integer. Let ![]() and let * denote the convolution on
and let * denote the convolution on![]() . We have
. We have
![]()
because ![]() as
as![]() , since
, since![]() , and
, and ![]()
Proof of Step 4. With the new representation of ![]() the summation in (41) becomes (42). It is enough to perform substitutions and then simplify the result.
the summation in (41) becomes (42). It is enough to perform substitutions and then simplify the result.
Proof of Step 5. We have
![]()
![]()
therefore
![]()
for some![]() . A given value i occurs for exactly
. A given value i occurs for exactly ![]() pairs
pairs![]() .
.
Proof of Step 6. We move summations over k1, k2 in (43) inside and summations over r1, r2, i outside. Our target is to identify convolution kernels defined in terms of variables k1, k2 and then, keeping variables r1, r2, i fixed, take the limit with respect to R. ![]() we denote the smallest integer larger or equal to a rational number q. We know that
we denote the smallest integer larger or equal to a rational number q. We know that ![]() for i = 1, 2. We observe that ki ranges over the integer interval
for i = 1, 2. We observe that ki ranges over the integer interval ![]() , i = 1, 2. We define convolution kernels
, i = 1, 2. We define convolution kernels ![]() as
as
![]()
Lemma 4.4 guaranties that as ![]() the expression
the expression
![]()
tends to![]() . We proved that (44) is the limit of (43).
. We proved that (44) is the limit of (43).
Proof of Step 7. Each number![]() ,
, ![]() has two possible representations. The first one as
has two possible representations. The first one as ![]() with
with ![]() and the second one as
and the second one as ![]() with
with![]() . The first case occurs for
. The first case occurs for![]() ,
, ![]() ,
, ![]() and the second case for
and the second case for![]() ,
, ![]() ,
, ![]() . For t = 0 we have only one representation of
. For t = 0 we have only one representation of ![]() as
as ![]() with
with![]() ,
,![]() . Function
. Function ![]() incorporates all these relations and allows us to subsitue summations with respect to r1, r2 by summations with t, s, therefore (44) becomes (45).
incorporates all these relations and allows us to subsitue summations with respect to r1, r2 by summations with t, s, therefore (44) becomes (45).
Proof of Step 8. We fix summation variables k, t of expression (45) and we consider the effect of the summation done with respect to s, i. By Lemma 4.3 we know that function ![]() takes two values
takes two values ![]() and
and![]() , therefore we conclude that points
, therefore we conclude that points![]() ,
, ![]() ,
, ![]() , represent a discrete vertical half line consisting of lattice points of Λ starting directly above the graph G. Lemma 4.3 also tells us that value
, represent a discrete vertical half line consisting of lattice points of Λ starting directly above the graph G. Lemma 4.3 also tells us that value ![]() is taken
is taken ![]() times and value
times and value ![]() the remaining
the remaining ![]() times. The first point of the discrete half line, located right above the graph G, corresponds to parameter values i = 0,
times. The first point of the discrete half line, located right above the graph G, corresponds to parameter values i = 0, ![]() , and it is repeated inside formula (45)
, and it is repeated inside formula (45) ![]() times. The jth point of it, j ≥ 2, with counting done upwards, corresponds to values
times. The jth point of it, j ≥ 2, with counting done upwards, corresponds to values![]() ,
, ![]() and
and![]() ,
, ![]() , and in (45) it comes with multiplicity
, and in (45) it comes with multiplicity![]() . Let
. Let ![]() represent the Euclidean and the vertical distances from the jth point,
represent the Euclidean and the vertical distances from the jth point, ![]() of the discrete half line to the graph G. Similarity relation of the triangle representing distances
of the discrete half line to the graph G. Similarity relation of the triangle representing distances ![]() with the triangle with vertices
with the triangle with vertices ![]() gives
gives ![]() Since the multiplicity inside (45) of the jth point of the discrete half line equals
Since the multiplicity inside (45) of the jth point of the discrete half line equals![]() , and variables k, t parameterize all discrete vertical half lines of U we conclude that (45) may be expressed as (47).
, and variables k, t parameterize all discrete vertical half lines of U we conclude that (45) may be expressed as (47).
Proof of Step 9. It is enough to combine together the outcomes of steps 1 - 8, i.e. all of the intermediate stages of the reduction process.
The proof of Corollary 1.3 follows directly from Theorems 1.1, 1.2.
Corollary 1.3. For any lattice ![]() satisfying condition
satisfying condition![]() , any generating function
, any generating function ![]() of a tight Gabor frame
of a tight Gabor frame![]() , any Λ lattice domain Ω, and any a, b > 0 satisfying
, any Λ lattice domain Ω, and any a, b > 0 satisfying![]() , there are a generating function
, there are a generating function ![]() of a tight Gabor frame
of a tight Gabor frame ![]() and a
and a ![]() lattice domain
lattice domain![]() , satisfying
, satisfying
![]() ,
, ![]() ,
, ![]() , for all
, for all![]() , and also
, and also ![]()
![]() . The rates of convergence of
. The rates of convergence of ![]() to
to ![]() and
and ![]() to
to ![]() are the same.
are the same.
Proof. It is enough to take ![]() transferring Λ onto
transferring Λ onto![]() ,
, ![]() ,
, ![]() , and apply Theorem 1.1. The existence and the form of the limits follows from Theorem 1.2.
, and apply Theorem 1.1. The existence and the form of the limits follows from Theorem 1.2.
4. Auxiliary Facts and Their Proofs
Transformation properties with respect to the metaplectic representation. A comprehensive presentation of the metaplectic representation from the point of view of phase space analysis is contained in Folland’s book [7] . The book by Lang [38] is an extensive reference on![]() . The Heisenberg group
. The Heisenberg group ![]() is the group obtained by defining on
is the group obtained by defining on ![]() the product
the product
![]()
where![]() ,
, ![]() and
and ![]() is the symplectic form defined on
is the symplectic form defined on![]() , i.e.
, i.e.
![]()
The Schrödinger representation of the group![]() , acting on
, acting on![]() , is then defined by
, is then defined by
![]()
We write ![]() when we separate the position component x from the momentum component
when we separate the position component x from the momentum component ![]() of a point z of the phase space
of a point z of the phase space![]() . The group
. The group![]() , consisting of
, consisting of ![]() matrices with real entries and determinant 1, acts on
matrices with real entries and determinant 1, acts on ![]() via automorphisms that leave the center
via automorphisms that leave the center ![]() of
of ![]() pointwise fixed, i.e. with
pointwise fixed, i.e. with ![]() For any fixed
For any fixed ![]() there is a unitary representation of
there is a unitary representation of![]() , acting on
, acting on![]() , defined as the composition
, defined as the composition ![]() with its restriction to the center of
with its restriction to the center of ![]() being a multiple of the identity. By the Stone-von Neumann theorem
being a multiple of the identity. By the Stone-von Neumann theorem ![]() is unitary equivalent to
is unitary equivalent to![]() , i.e. there is an intertwining unitary operator
, i.e. there is an intertwining unitary operator ![]() acting on
acting on ![]() such that for all
such that for all ![]()
![]()
By Schur’s lemma, ![]() is determined up to a phase factor
is determined up to a phase factor![]() . It turns out that the phase ambiguity is really a sign, so that
. It turns out that the phase ambiguity is really a sign, so that ![]() lifts to a representation of the double cover of the group
lifts to a representation of the double cover of the group![]() . The constructed representation of the double cover of
. The constructed representation of the double cover of ![]() is called the metaplectic representation.
is called the metaplectic representation.
The representations ![]() and
and ![]() can be combined and give rise to the extended metaplectic representation
can be combined and give rise to the extended metaplectic representation![]() , the composition of
, the composition of![]() , defined on
, defined on![]() , with
, with![]() , defined on the double cover of
, defined on the double cover of![]() . From the point of view of the interpretation as a phase space action, the phase factors do not matter, therefore we remove them and treat
. From the point of view of the interpretation as a phase space action, the phase factors do not matter, therefore we remove them and treat ![]() as a projective representation of
as a projective representation of![]() , and
, and ![]() as a projective representation of the semidirect product
as a projective representation of the semidirect product ![]() with the group law
with the group law
![]() (57)
(57)
The extended metaplectic representation provides all affine transformations of the phase space![]() . For
. For ![]() the unitary operator
the unitary operator![]() , defined up to a phase factor, expresses the analytic action on
, defined up to a phase factor, expresses the analytic action on![]() . The affine geometric action on
. The affine geometric action on ![]() is expressed by the law
is expressed by the law
![]() (58)
(58)
The extended metaplectic representation is a convenient setup for performing computations involving compositions of the Schrödinger and the metaplectic representations.
Both Gabor multipliers (2) and lattice boundary forms (4) have natural transformation properties with respect to the projective metataplectic representation. These properties are important ingredient of our proofs. We will deduce them out of the the fundamental lemma formulated below.
Lemma 4.1. Let ![]() be a lattice,
be a lattice, ![]() a tight Gabor frame with the generating function
a tight Gabor frame with the generating function![]() ,
, ![]() , and
, and![]() . Then
. Then
1) ![]() is a lattice,
is a lattice, ![]() a tight Gabor frame with the generating function
a tight Gabor frame with the generating function![]() , and
, and
![]() (59)
(59)
2)![]() , and
, and
![]() (60)
(60)
Proof. Clearly ![]() is a lattice, since A is linear and invertible. Group law (57) and affine action rule (58) allow us to identify the phase space
is a lattice, since A is linear and invertible. Group law (57) and affine action rule (58) allow us to identify the phase space ![]() with the subgroup
with the subgroup ![]() of
of![]() . Since
. Since![]() , by substituting
, by substituting ![]() we obtain
we obtain
![]()
The above calculation shows that ![]() is a tight Gabor frame, it is enough to take the constant function equal to 1 for b. It also verifies formula (60). Formula (59) follows by a similar calculation,
is a tight Gabor frame, it is enough to take the constant function equal to 1 for b. It also verifies formula (60). Formula (59) follows by a similar calculation,
![]()
Symbolic calculus of Gabor multipliers. Let us assume that ![]() is a lattice, and
is a lattice, and ![]() a tight Gabor frame defined on it. Let us define the mapping
a tight Gabor frame defined on it. Let us define the mapping ![]() by the formula
by the formula
![]()
Tight frame properties of ![]() imply that
imply that ![]() is an isometry, and that the operator
is an isometry, and that the operator ![]() defined as
defined as
![]()
is the orthogonal projection onto the range of![]() . Gabor multiplier
. Gabor multiplier ![]() is parametrized by the generating function
is parametrized by the generating function ![]() of a tight Gabor frame
of a tight Gabor frame ![]() and a symbol
and a symbol![]() . Let us recall that it is a bounded operator acting on
. Let us recall that it is a bounded operator acting on ![]() defined as
defined as
![]()
It is convenient to describe Gabor multiplier ![]() in terms of the Toeplitz operator
in terms of the Toeplitz operator ![]() acting on
acting on![]() ,
, ![]() denotes the operator of multiplication by b. The isometry
denotes the operator of multiplication by b. The isometry ![]() allows us to identify
allows us to identify ![]() with the upper left corner of the matrix representation of the operator
with the upper left corner of the matrix representation of the operator ![]() with respect to the orthogonal decomposition
with respect to the orthogonal decomposition![]() . Basic properties of the symbolic calculus of Gabor multipliers can be deduced out of the properties of the symbolic calculus of Toeplitz operators. Hankel operator
. Basic properties of the symbolic calculus of Gabor multipliers can be deduced out of the properties of the symbolic calculus of Toeplitz operators. Hankel operator ![]() acting on
acting on ![]() measures to what degree the mapping
measures to what degree the mapping ![]() fails to be a homomorphism. The algebraic formula
fails to be a homomorphism. The algebraic formula
![]()
expresses this relationship quantitatively and it is the main conceptual ingredient of the argument that allows us to write down the projection functional
![]()
as the square of the Hilbert-Schmidt norm the matrix
![]()
where![]() .
.
Lemma 4.2. Let ![]() be a tight Gabor frame and
be a tight Gabor frame and ![]() a finite set. Then
a finite set. Then
![]()
Proof. The non-zero eigenvalues of the localization operator ![]() coincide with the non-zero eigenvalues of the Toeplitz operator
coincide with the non-zero eigenvalues of the Toeplitz operator ![]() and the non-zero eigenvalues of the operator
and the non-zero eigenvalues of the operator![]() . The first fact follows from the identification of
. The first fact follows from the identification of ![]() with the upper left corner of the matrix representation of
with the upper left corner of the matrix representation of ![]() with respect to the decomposition of
with respect to the decomposition of ![]() into the range of
into the range of ![]() and its orthogonal complement. The second fact follows since for a compact operator T the non-zero eigenvalues of
and its orthogonal complement. The second fact follows since for a compact operator T the non-zero eigenvalues of ![]() and
and ![]() are the same. We observe that
are the same. We observe that
![]()
and that
![]()
Therefore we obtain
![]()
and this finishes the proof.
Lattice slopes of rational lines. For an integer t we define the t-slope of the line ![]() at an integer argument s as
at an integer argument s as
![]() (61)
(61)
where ![]() is the smallest integer larger than x, and
is the smallest integer larger than x, and ![]() is the largest integer smaller or equal to x. The t-slope at s is simply the smallest difference between integer values above the graph at
is the largest integer smaller or equal to x. The t-slope at s is simply the smallest difference between integer values above the graph at ![]() and below or on the graph at s. We interpret it as the lattice slope corresponding to making t-steps to the right of s. We do not normalize the t-slope, i.e. we do not divide it by the number of steps. As we have already seen function Rt defined in (46) is the principal analytic component of the boundary form. It occurs that it may be interpreted as the
and below or on the graph at s. We interpret it as the lattice slope corresponding to making t-steps to the right of s. We do not normalize the t-slope, i.e. we do not divide it by the number of steps. As we have already seen function Rt defined in (46) is the principal analytic component of the boundary form. It occurs that it may be interpreted as the
t-slope of the rational line![]() . Indeed, let
. Indeed, let ![]() be the t-slope of the line
be the t-slope of the line ![]() at s. Direct inspec-
at s. Direct inspec-
tion shows, that values ![]() and
and ![]() coincide for
coincide for![]() . Function
. Function ![]() is periodic with period n and we may regard it as defined on the cyclic group
is periodic with period n and we may regard it as defined on the cyclic group![]() .
.
Our primary geometric concern are the values of lattice slopes and the frequencies with which they occur. Observe that ![]() for all
for all![]() . If
. If![]() , then the only possible value of t is 0 and again 1 is the only value of Rt. If however
, then the only possible value of t is 0 and again 1 is the only value of Rt. If however ![]() and
and![]() , then Rt takes precisely two values. The next lemma describes those values and the frequencies with which they occur.
, then Rt takes precisely two values. The next lemma describes those values and the frequencies with which they occur.
Lemma 4.3. Let m, n be a pair of relatively prime integers. Assume that![]() . Let
. Let ![]() be a fixed number. Function
be a fixed number. Function ![]() defined for arguments
defined for arguments ![]() by formula (46) takes two distinct
by formula (46) takes two distinct
values ![]() and
and![]() . Value
. Value ![]() is taken
is taken ![]() times, and value
times, and value ![]() is taken the remaining
is taken the remaining ![]() times.
times.
Proof. We know that Rt and St are equal. It is therefore enough to prove Lemma 4.3 with St instead of Rt. Let![]() . Line
. Line ![]() crosses vertical lines x = s at points of the form
crosses vertical lines x = s at points of the form![]() , where l is an
, where l is an
integer and![]() . Numbers m, n are relatively prime, therefore each value of r occurs precisely once for an appropriate value of
. Numbers m, n are relatively prime, therefore each value of r occurs precisely once for an appropriate value of![]() . Observe that the set of values
. Observe that the set of values![]() ,
,
![]() is the same as the set of t-slopes at 0 of the lines
is the same as the set of t-slopes at 0 of the lines![]() ,
,![]() . Indeed an integer shift of coordinates allows us to view each segment starting at
. Indeed an integer shift of coordinates allows us to view each segment starting at ![]() and ending at
and ending at ![]() as a segment starting at
as a segment starting at ![]() and ending at
and ending at ![]() for an appropriate value of r. Line
for an appropriate value of r. Line ![]() crosses the vertical line
crosses the vertical line ![]() at a point
at a point ![]() with l an integer and
with l an integer and![]() . All lines
. All lines ![]() with
with ![]() have the same t-slope at 0 as the line
have the same t-slope at 0 as the line![]() . The t-slope jumps up by 1 for
. The t-slope jumps up by 1 for ![]() and keeps this value for all the remaining
and keeps this value for all the remaining![]() . We conclude that function St takes two values
. We conclude that function St takes two values ![]() and
and![]() . The first value is taken
. The first value is taken ![]() times and the second value u times. We need to verify that
times and the second value u times. We need to verify that![]() . Indeed,
. Indeed, ![]() , therefore
, therefore![]() ,
, ![]() and
and![]() .
.
Approximation to the identity by Fejér’s kernel. In the lemma that follows we quote a well known approximation to the identity property of the Fejér’s kernel. We translate the original property from the group of one dimensional torus to the group of integers. For ![]() by
by ![]() we denote the convolution of f and g, defined as
we denote the convolution of f and g, defined as
![]()
Lemma 4.4. [39] If![]() , then
, then
![]()
where ![]() stands for the inner product of
stands for the inner product of![]() .
.
Invariance properties of the restricted kernel KR. Let us recall that kernel
![]()
where ![]() is a
is a ![]() domain,
domain, ![]() and
and ![]() was defined in (39). This section presents invariance properties of kernel
was defined in (39). This section presents invariance properties of kernel ![]() needed at various stages of the process of reduction. Let
needed at various stages of the process of reduction. Let![]() , be the group of automorphisms of
, be the group of automorphisms of ![]() (or
(or![]() ), i.e. the semi-direct product of sign changes and permutations of variables (see [23] page 110). Let
), i.e. the semi-direct product of sign changes and permutations of variables (see [23] page 110). Let ![]() be the group of affine transformations of
be the group of affine transformations of ![]() consisting of translations and automorphisms of
consisting of translations and automorphisms of![]() . The elements of
. The elements of ![]() are represented as pairs
are represented as pairs![]() , where
, where![]() ,
,![]() . The group law has the form
. The group law has the form![]() .
.
Lemma 4.5. Let ![]() and let
and let![]() . After the change of variables
. After the change of variables ![]() ,
, ![]() the restricted kernel
the restricted kernel ![]()
![]()
becomes
![]()
For any ![]() domain Ω and any line segment
domain Ω and any line segment ![]() it is possible to choose a transformation
it is possible to choose a transformation
![]() such that
such that ![]() is a segment of the graph of
is a segment of the graph of![]() , where
, where![]() ,
, ![]() ,
, ![]() ,
,
m, n are relatively prime, and the portion of ![]() close to
close to ![]() is placed below
is placed below![]() , the portion of
, the portion of ![]() close to
close to ![]() is placed above
is placed above![]() . If the line segment l does not contain lattice points in its interior,
. If the line segment l does not contain lattice points in its interior,
then we may assume that![]() .
.
Proof. The proof of the first part, the formula for the coordinate change is a straightforward computation which makes use of the fact that![]() . The proof of the second part follows the process of inspecting the list of all possible positions of the segment l, which takes into account the placement of Ω and
. The proof of the second part follows the process of inspecting the list of all possible positions of the segment l, which takes into account the placement of Ω and ![]() relative to l, and indicating in each case the coordinate change
relative to l, and indicating in each case the coordinate change ![]() needed to accomplish the target. It is also a direct computation.
needed to accomplish the target. It is also a direct computation.
Asymptotic limits of the restricted kernel KR. The following two lemmas are the main technical tools behind the reduction process of general lattice domains to vertical strip domains. In the first lemma we deal with separated supports of variables![]() . The second lemma is more delicate, it treats the case of variables
. The second lemma is more delicate, it treats the case of variables ![]() restricted to bounded cones located outside and inside Ω, with their sides being segments of rational lines, and their common vertex being a lattice point of the boundary of Ω.
restricted to bounded cones located outside and inside Ω, with their sides being segments of rational lines, and their common vertex being a lattice point of the boundary of Ω.
Lemma 4.6. Suppose that there is ![]() such that for all sufficiently large R nonnegative kernel
such that for all sufficiently large R nonnegative kernel![]() ,
, ![]() satisfies
satisfies
![]()
Then ![]()
Proof. For each ![]() we have
we have
![]()
Let![]() . We observe that
. We observe that
![]()
where for ![]() by
by ![]() we denote
we denote![]() . Since
. Since ![]() we obtain
we obtain
![]()
Lemma 4.7. Suppose that there are two closed, bounded cones![]() ,
, ![]() ,
, ![]() , with their sides
, with their sides
being segments of rational lines, their apertures smaller than ![]() and their intersection being their common vertex, a lattice point of the boundary of Ω. Suppose also that for all sufficiently large R nonnegative kernel
and their intersection being their common vertex, a lattice point of the boundary of Ω. Suppose also that for all sufficiently large R nonnegative kernel
![]() satisfies
satisfies
![]()
Then
![]()
Proof. We observe that in view of Lemma 4.6 we may substitute cones C1, C2 by restricted cones![]() ,
, ![]() , where
, where ![]() is the Euclidean disk with radius
is the Euclidean disk with radius ![]() and center v, the common vertex of C1, C2. We may take the radius
and center v, the common vertex of C1, C2. We may take the radius ![]() arbitrarily small. We choose a lattice line l passing
arbitrarily small. We choose a lattice line l passing
through v and separating C1 and C2. Lemma 4.5 allows us to assume that line l has the form![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , that the origin is the common vertex of C1, C2, and that C1 lies above l and C2 below l.
, that the origin is the common vertex of C1, C2, and that C1 lies above l and C2 below l.
If![]() , i.e. line l is not horizontal, then we extend the lattice
, i.e. line l is not horizontal, then we extend the lattice ![]() to lattice
to lattice![]() ,
,
![]() (62)
(62)
and kernel F to kernel![]() ,
,
![]() (63)
(63)
where![]() ,
, ![]() ,
,![]() . We observe that line l becomes a horizontal line with re- spect to
. We observe that line l becomes a horizontal line with re- spect to![]() . We obtain
. We obtain
![]() (64)
(64)
In the next step we bring the sum (64) to a computable form. We introduce an integer cone![]() ,
, ![]() ,
, ![]() with a sufficiently large aperture
with a sufficiently large aperture ![]() in order to capture all points of
in order to capture all points of ![]() of (64). Constant
of (64). Constant ![]() is the magnification factor needed to switch from
is the magnification factor needed to switch from ![]() to an integer lattice. Parameter
to an integer lattice. Parameter ![]() of the integer cone accounts for this magnification. We estimate (64) by
of the integer cone accounts for this magnification. We estimate (64) by
![]() (65)
(65)
where ![]() is
is ![]() adjusted to the new coordinate system adapted to representing l as a horizontal line. Let
adjusted to the new coordinate system adapted to representing l as a horizontal line. Let![]() , where
, where![]() ,
,![]() . Then
. Then ![]() and x is represented as
and x is represented as ![]() for at most
for at most ![]() pairs
pairs![]() . Therefore we may estimate (65) by
. Therefore we may estimate (65) by
![]() (66)
(66)
Let![]() , where
, where![]() . Then
. Then ![]() and y is represented as
and y is represented as ![]() for exactly
for exactly ![]() pairs
pairs![]() . We may estimate (66) by
. We may estimate (66) by
![]() (67)
(67)
Since ![]() for sufficiently large
for sufficiently large![]() , and
, and ![]() we conclude that (67) may be estimated by
we conclude that (67) may be estimated by
![]()
This concludes the proof that since the constants M, ![]() depend only on the cones C1, C2, condition Φ guaranties that
depend only on the cones C1, C2, condition Φ guaranties that![]() , and we are allowed to take δ arbitrarily small.
, and we are allowed to take δ arbitrarily small.
Acknowledgments
The authors would like to thank ESI (Erwin Schrödinger Institute, University of Vienna), where the joint work on this paper began (Thematic Programme: Modern Methods of Time-Frequency Analysis II), and CIRM (Centre international de recontres mathématique, Luminy, Marseille), where the three authors had the chance to complete their work during the period of Hans Feichtinger’s Morlet Chair.
Cite this paper
H. G.Feichtinger,K.Nowak,M.Pap, (2015) Asymptotic Boundary Forms for Tight Gabor Frames and Lattice Localization Domains. Journal of Applied Mathematics and Physics,03,1316-1342. doi: 10.4236/jamp.2015.310160
References
- 1. Gröchenig, K. and Stöckler, J. (2013) Gabor Frames and Totally Positive Functions. Duke Mathematical Journal, 162, 1003-1031.
http://dx.doi.org/10.1215/00127094-2141944
- 2. De Mari, F. and Nowak, K. (2001) Analysis of the Affine Transformations of the Time-Frequency Plane. Bulletin of the Australian Mathematical Society, 63, 195-218.
http://dx.doi.org/10.1017/S0004972700019274
- 3. Daubechies, I. (1992) Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series, No. 6, SIAM, Philadelphia.
- 4. Landau, H.J. and Widom, H. (1980) Eigenvalue Distribution of Time and Frequency Limiting. Journal of Mathematical Analysis and Applications, 77, 469-481.
http://dx.doi.org/10.1016/0022-247X(80)90241-3
- 5. Landau, H.J. (1993) On the Density of Phase-Space Expansions. IEEE Transactions on Information Theory, 39, 1152-1156.
http://dx.doi.org/10.1109/18.243434
- 6. Maz’ya, V.G. and Shaposhnikova, T.O. (2011) Sobolev Spaces: With Applications to Elliptic Partial Differential Equations (Grundlehren der Mathematischen Wissenschaften 342). Springer, Berlin.
- 7. Folland, G. (1989) Harmonic Analysis in Phase Space. Princeton University Press, Princeton.
- 8. Zhu, K. (2012) Analysis on Fock Spaces. Graduate Texts in Mathematics, Volume 263, Springer, New York.
- 9. Feichtinger, H.G. and Nowak, K. (2001) A Szegö-Type Theorem for Gabor-Toeplitz Localization Operators. The Michigan Mathematical Journal, 49, 13-21.
http://dx.doi.org/10.1307/mmj/1008719032
- 10. De Mari, F., Feichtinger, H.G. and Nowak, K. (2002) Uniform Eigenvalue Estimates for Time-Frequency Localization Operators. Journal of the London Mathematical Society, 65, 720-732.
http://dx.doi.org/10.1112/S0024610702003101
- 11. Nowak, K. Optimal Localization Domains for Gabor-Toeplitz Operators. Unpublished Manuscript.
- 12. Dörfler, M. and Gröchenig, K. (2011) Time-Frequency Partitions and Characterizations of Modulation Spaces with Localization Operators. Journal of Functional Analysis, 260, 1903-1924.
http://dx.doi.org/10.1016/j.jfa.2010.12.021
- 13. Gröchenig, K.-H. and Toft, J. (2011) Isomorphism Properties of Toeplitz Operators in Time-Frequency Analysis. Journal d’Analyse Mathematique, 114, 255-283.
- 14. Gröchenig, K. and Toft, J. (2013) The Range of Localization Operators and Lifting Theorems for Modulation and Bargmann-Fock Spaces. Transactions of the American Mathematical Society, 365, 4475-4496.
http://dx.doi.org/10.1090/S0002-9947-2013-05836-9
- 15. Döpfner, K.A. (2012) Quality of Gabor Multipliers for Approximation of Hilbert-Schmidt Operators. Master’s Thesis, Department of Mathematics, University of Vienna, Vienna.
- 16. Gröchenig, K. (2011) Representation and Approximation of Pseudodifferential Operators by Sums of Gabor Multipliers. Applicable Analysis, 90, 385-401.
http://dx.doi.org/10.1080/00036811.2010.499507
- 17. Dörfler, M. and Torrésani, B. (2010) Representations of Operators in the Time-Frequency Domain and Generalized Gabor Multipliers. Journal of Fourier Analysis and Applications, 16, 261-293.
http://dx.doi.org/10.1007/s00041-009-9085-x
- 18. Cordero, E., Nicola, F. and Rodino, L. (2010) Time-Frequency Analysis of Fourier Integral Operators. Communications on Pure and Applied Analysis, 9, 1-21.
- 19. Cordero, E., Gröchenig, K. and Nicola, F. (2012) Approximation of Fourier Integral Operators by Gabor Multipliers. Journal of Fourier Analysis and Applications, 18, 661-684.
http://dx.doi.org/10.1007/s00041-011-9214-1
- 20. Feichtinger, H.G., Nowak, K. and Pap, M. (2014) Spectral Properties of Toeplitz Operators Acting on Gabor Type Reproducing Kernel Hilbert Spaces. In: Rassias, T.M. and Pardalos, P.M., Eds., Mathematics without Boundaries: Surveys in Pure Mathematics, Springer, New York, 163-180.
- 21. Nowak, K. (1996) Local Toeplitz Operators Based on Wavelets: Phase Space Patterns for Rough Wavelets. Studia Mathematica, 119, 37-64.
- 22. Feichtinger, H.G. and Nowak, K. (2003) A First Survey of Gabor Multipliers. In: Fiechtinger, H.G. and Strohmer, T., Eds., Advances in Gabor Analysis, Birkhäuser, Boston, 99-128.
- 23. Martinet, J. (2003) Perfect Lattices in Euclidean Spaces (Grundlehren der mathematischen Wissenschaften, Volume 327). Springer, Berlin.
http://dx.doi.org/10.1007/978-3-662-05167-2
- 24. Stein, E.M. (1993) Harmonic Analysis, Real-Variable Methods, Orthogonality, and Oscillatory Integrals. Princeton University Press, Princeton.
- 25. Nowak, W.G. (2004) Lattice Points in a Circle: An Improved Mean-Square Asymptotics. Acta Arithmetica, 113, 259-272.
http://dx.doi.org/10.4064/aa113-3-4
- 26. Christensen, O. (2003) An Introduction to Frames and Riesz Bases. Birkhäuser, Boston.
http://dx.doi.org/10.1007/978-0-8176-8224-8
- 27. Flandrin, P. (1999) Time-Frequency/Time-Scale Analysis. Academic Press, San Diego.
- 28. Gröchenig, K. (2001) Foundations of Time-Frequency Analysis. Birkhäuser, Boston.
- 29. Wojtaszczyk, P. (1997) A Mathematical Introduction to Wavelets. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511623790
- 30. Feichtinger, H.G. and Strohmer, T. (1998) Gabor Analysis and Algorithms. Theory and Applications. Birkhäuser, Boston.
- 31. Feichtinger, H.G. and Strohmer, T. (2003) Advances in Gabor Analysis. Birkhäuser, Boston.
- 32. Balan, R. (2008) The Noncommutative Wiener Lemma, Linear Independence, and Spectral Properties of the Algebra of Time-Frequency Shift Operators. Transactions of the American Mathematical Society, 360, 3921-3941.
http://dx.doi.org/10.1090/S0002-9947-08-04448-6
- 33. Casazza, P.G. (2000) The Art of Frame Theory. Taiwanese Journal of Mathematics, 4, 129-201.
- 34. Heil, C. (2007) History and Evolution of the Density Theorem for Gabor Frames. Journal of Fourier Analysis and Applications, 13, 113-166.
http://dx.doi.org/10.1007/s00041-006-6073-2
- 35. Gröchenig, K. and Leinert, M. (2003) Wiener’s Lemma for Twisted Convolution and Gabor Frames. Journal of the American Mathematical Society, 17, 1-18.
- 36. Luef, F. Private Communication.
- 37. Feichtinger, H.G. and Kaiblinger, N. (2003) Varying the Time-Frequency Lattice of Gabor Frames. Transactions of the American Mathematical Society, 356, 2001-2023.
- 38. Lang, S. (1998) SL2(R), Graduate Texts in Mathematics. Volume 105, Springer, New York.
- 39. Katznelson, Y. (1976) An Introduction to Harmonic Analysis. Dover Publications, New York.



 defined by two parameters, the generating function
defined by two parameters, the generating function  of a tight Gabor frame
of a tight Gabor frame , indexed by a lattice
, indexed by a lattice , and a domain
, and a domain  whose boundary consists of line segments connecting certain points of
whose boundary consists of line segments connecting certain points of . We provide an explicit formula for the boundary form
. We provide an explicit formula for the boundary form , the normalized limit of the projection functional
, the normalized limit of the projection functional , where
, where  are the eigenvalues of the localization operators
are the eigenvalues of the localization operators  applied to dilated domains
applied to dilated domains , R is an integer and
, R is an integer and  is the area of the fundamental domain. The boundary form expresses quantitatively the asymptotic interactions between the generating function
is the area of the fundamental domain. The boundary form expresses quantitatively the asymptotic interactions between the generating function  and the oriented boundary
and the oriented boundary  from the point of view of the projection functional, which measures to what degree a given trace class operator fails to be an orthogonal projection. Keeping the area of the localization domain
from the point of view of the projection functional, which measures to what degree a given trace class operator fails to be an orthogonal projection. Keeping the area of the localization domain  bounded above corresponds to controlling the relative dimensionality of the localization problem.
bounded above corresponds to controlling the relative dimensionality of the localization problem.
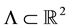 be a lattice, i.e. a discrete co-compact subgroup of
be a lattice, i.e. a discrete co-compact subgroup of






































































































































































































































































































































































































































































































































































































































































































































































































































































































































