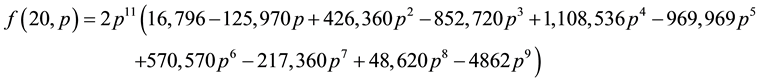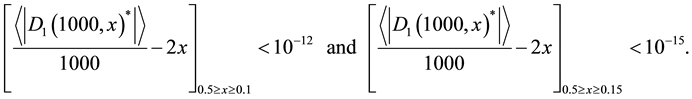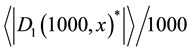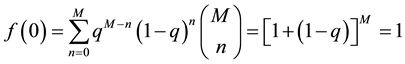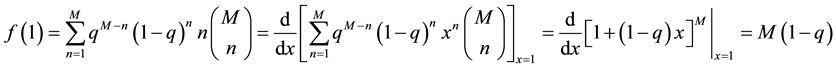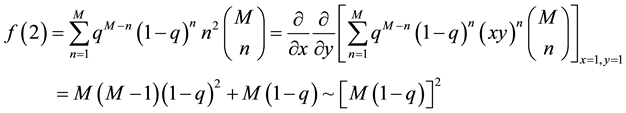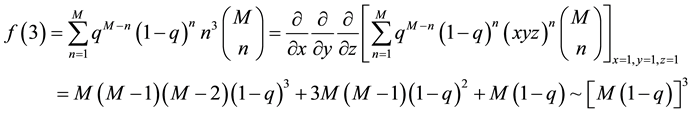Journal of Applied Mathematics and Physics
Vol.03 No.09(2015), Article ID:59836,8 pages
10.4236/jamp.2015.39143
How Far Can a Biased Random Walker Go?
Zhongjin Yang1, Cassidy Yang2
1Cantigny Court, Naperville, IL, USA
2Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA, USA
Email: yangzhongjin@gmail.com, cyyang@caltech.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 August 2015; accepted 20 September 2015; published 23 September 2015
ABSTRACT
The random walk (RW) is a very important model in science and engineering researches. It has been studied over hundreds years. However, there are still some overlooked problems on the RW. Here, we study the mean absolute distance of an N-step biased random walk (BRW) in a d- dimensional hyper-cubic lattice. In this short paper, we report the exact results for d = 1 and approximation formulae for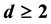 .
.
Keywords:
Biased Random Walk, Monte Carlo Simulations, Stochastic Process

1. Introduction
As a mathematical model, the random walk (RW) has been widely used in almost all branches of sciences and engineering [1] -[9] . Although the unbiased random walk has been studied extensively in literature, the biased random walk (BRW) has not been studied carefully in some cases.
In this short paper, we first give a brief description of the conventional results, and then report our study with some results on the BRW.
Let us consider the one dimensional BRW: a probability p of going forward and a probability (1 − p) of going backward with uniform step length L. Traditionally, the average distance gone in one step is expressed as:
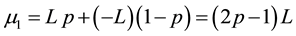 (1)
(1)
The variance of a one step BRW can be calculated as:
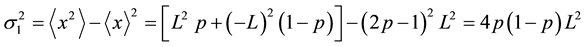 (2)
(2)
After N such steps, the mean distance becomes
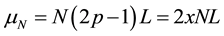 . (3)
. (3)
In the last expression, 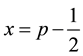 is used. When
is used. When  (i.e.,
(i.e., ), the mean distance becomes zero. The
), the mean distance becomes zero. The
variance of the N steps is
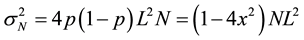 (4)
(4)
The standard deviation of the N steps is
 (5)
(5)
In the case of the pure random walk (RW), i.e. when 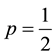 (
( ), the standard deviation of the N-step
), the standard deviation of the N-step
RW is
 . (6)
. (6)
This value, known widely in literature, is usually considered as the absolute distance of an N-step RW. This expression is independent of the dimensions of the lattice.
However, the mean absolute distance of the N-step RW in a d-dimensional hyper-cubic lattice cannot be expressed by (6), but is the following formula [10]
 , (7)
, (7)
where 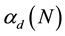 is a monotonic increasing function of dimension d with saturation value of one:
is a monotonic increasing function of dimension d with saturation value of one:
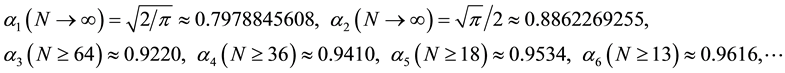 (8)
(8)
We compute the absolute distance for the N-step biased random walk (BRW). We find that (3) is a fairly good
approximation for a reasonably large N and p away from the neighborhood of .
.
In Section 2, the exact results for d = 1 are presented. The approximation results for higher dimensions are shown in Section 3. A brief discussion is given afterward. A warning: it is possible that some of our results might have been already published in earlier literatures unknown to us.
For convenience, without loss of generality, we choose a step length of L = 1 in hereafter expressions.
2. Exact Results for d = 1
For an N step biased random walker (BRW), if the walker moves forward n steps with probability p, and moves backwards (N ? n) steps with probability 1 − p, this is a binomial process with probability p. The absolute distance from the origin will be

After taking the weighted configuration average, the mean absolute distance of the one-dimensional BRW can be expressed as:
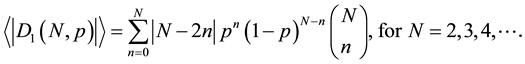
Using Mathematica [11] , we obtain the following relationship:

where 
Furthermore, we obtain the following relationship (via Mathematica):
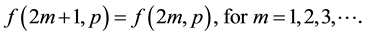
The 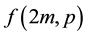
For convenience, we have listed some exact results for small values of N as follows:
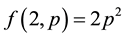

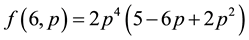

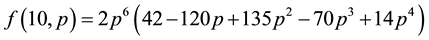
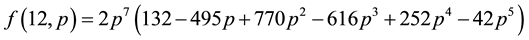
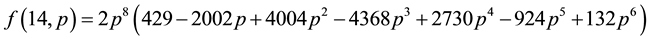
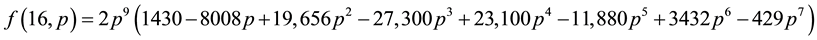
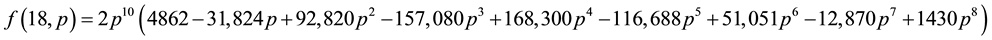
Further algebraic calculations yield the following recursion equations (for an even N, let N = 2 m in the following expressions):

i.e.

Additionally, because 

If we let 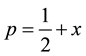
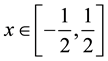

When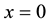
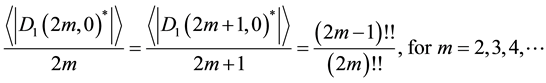
In order to obtain these results, we use the following identity:

Therefore, Equation (15) can be expressed as a polynomial of x2:
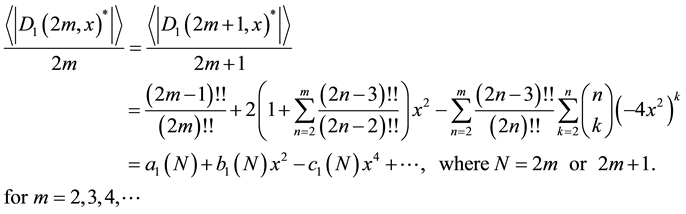
In order to see the quantitative behavior of the averaged absolute distance as a function of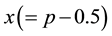
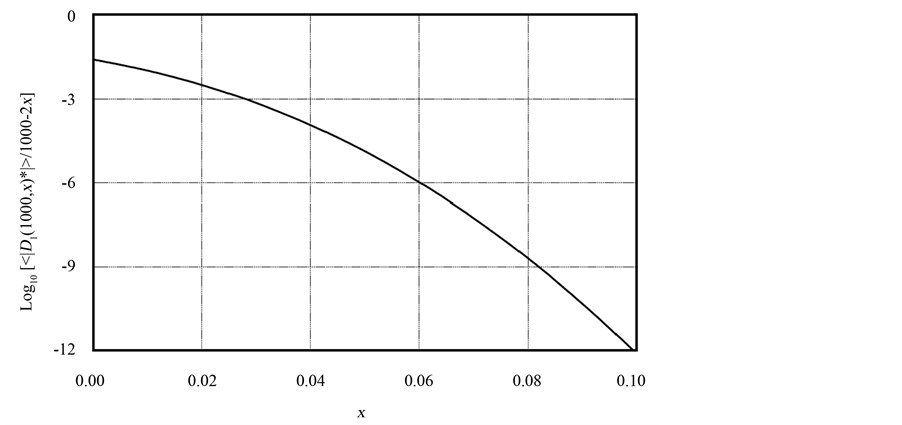
We have computed some typical values of the approximation error as follows (and partially shown in Figure 2):
In the range for which the linear approximation is invalid (the neighborhood of
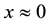
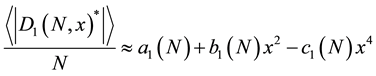
where
Figure 1. The normalized plot of the averaged absolute distance 
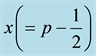


Figure 2. The semi-log plot of the difference between the normalized absolute distance and the linear approximation vs. the biased probability x. For accuracy reasons
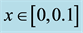
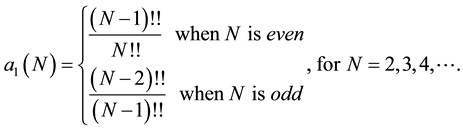
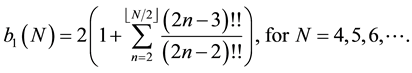

The relationship between 
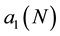


by Equation (7). The second term coefficient 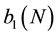
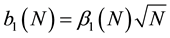
coefficient 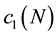
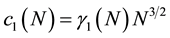
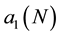
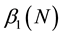

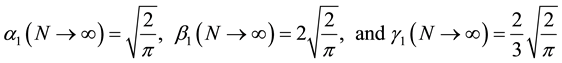
We also compute the next three terms of Equation (18):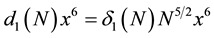


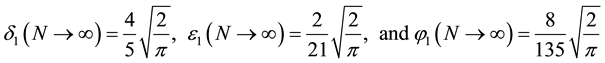
From Figure 3, it is easy to see that, for a reasonable large N, the coefficients are very close to their asymptotic values. Therefore, in the neighborhood of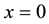
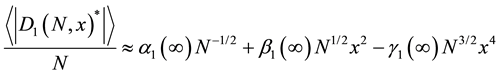
Figure 3. The coefficients, 
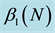


To verify the validity of the approximation (25), we plot 
with exact results vs. the 3-term approximation Equation (25) for small values of x in Figure 4. It is easy to see that formula (25) is a very good approximation in the neighborhood of
3. For
For a 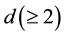


along the i'th coordinate. We define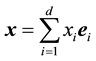
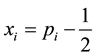

are the unit vectors. The absolute value of 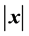
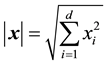
nent is: 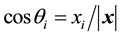
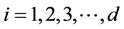
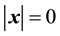

In the neighborhood of
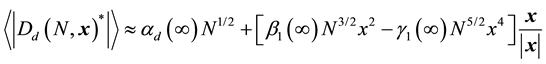
Here, 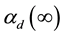
Alternatively, we can consider the multidimensional BRW by transposing the coordinate system so that only one direction is biased. For instance, we can consider a diffusion process via an interface in which there is a pressure applied in the direction perpendicular to the interface. In this situation, all directions except the (biased) direction perpendicular to the interface follow a pure random walk. This model can be applied to many diffusion problems in physics and chemistry. Generally speaking, we can express the dimension, d as
Figure 4. The normalized plot of the averaged absolute distance 
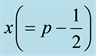

distance of the g-dimensional 
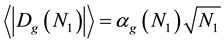

lattice, the (pure random walk) displacement is perpendicular to the (biased) direction of the BRW. In many problems, we are only concerned with the absolute distance in the (biased) direction, i.e., the projection portion of the total absolute distance. For this reason, we can model it as a modified 1d approach as follows: a probability q walking in the g-dimensional hyper-cubic lattice, a probability 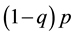

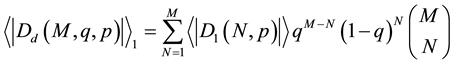
We study two cases, one for reasonably large p and the other in the neighborhood of
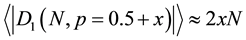
Substituting this into (28) and using the results of the Appendix yields:
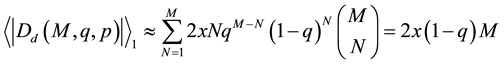
It is not surprising that the modification of higher dimensions on the 1d result requires only multiplication of the probability factor
For the second case, i.e., in the neighborhood of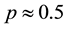

where
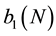

Using the 1d results, (31) can be estimated to be a very simple formula:

where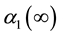
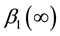
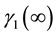
4. Discussion and Concluding Remarks
The biased random walk has widely applications in various fields: for examples, a pressured diffusion process, an ionic injection with bombardment, a ballistic transport, financial market data, etc. For most natural phenomena and engineering processes, the particle number is about the order or a fraction of the Avogadro’s constant (~1023), the traditional treatment is good enough. However, the financial data and some high precision experimental data are far away from a large number, say 1010. For example in financial industry, the most active index futures, SP500, has only the order of 105 open interest contracts before rolling the date. The daily trading volume is one or two order smaller than the open interest. Therefore, when the particle number is not large enough, one has to consider the new behavior. The present results are just the better quantitative descriptions for those phenomena. In some high precision experiments in physical sciences, one may have to measure parameters with small amount of particles. To quantify the property, the present results can provide better mathematical expressions.
Acknowledgements
The authors would like to Angel Yang for her helpful discussion.
Cite this paper
ZhongjinYang,CassidyYang, (2015) How Far Can a Biased Random Walker Go?. Journal of Applied Mathematics and Physics,03,1159-1167. doi: 10.4236/jamp.2015.39143
References
- 1. Feynman, R.P., Leighton, R.B. and Sands, M. (1963) Feynman Lectures on Physic. Addison-Wesley, New York, Vol. 1, 6-5, 41-9.
- 2. Whitney, C.A. (1990) Random Processes in Physical Systems. Wiley, New York, 37.
- 3. Uhlenbeck, G.E. and Ornstein, L.S. (1930) On the Theory of the Brownian Motion. Physical Review Letters, 36, 823.
http://dx.doi.org/10.1103/PhysRev.36.823 - 4. Grimmett, G. and Stirzaker, D. (2001) Probability and Random Processes. Oxford University Press, Oxford.
- 5. van Kampen, N.G. (2007) Stochastic Processes in Physics and Chemistry. 3rd Edition, Elsevier, Amsterdam.
- 6. Gardiner, C.W. (2004) Handbook of Stochastic Methods. 3rd Edition, Springer, Berlin.
http://dx.doi.org/10.1007/978-3-662-05389-8 - 7. Borodin, A.N. and Salminen, P. (2002) Handbook of Brownian Motion—Facts and Formulae. 2nd Edition, Birkhauser, Basel.
http://dx.doi.org/10.1007/978-3-0348-8163-0 - 8. Codling, E.A. (2003) Biased Random Walks in Biology. Ph.D. Thesis, University of Leeds, Leeds.
- 9. Stauffer, D. (1985) Introduction to Percolation Theory. Talor & Francis, London.
http://dx.doi.org/10.4324/9780203211595 - 10. Sun, T. and Yang, Z.J. (1992) How Far Can a Random Walker Go? Physica A: Statistical Mechanics and Its Applications, 182, 599-606.
http://dx.doi.org/10.1016/0378-4371(92)90024-K - 11. Wolfram, S. (2003) Mathematica. 5th Edition, Wolfram Media, Champaign.
Appendix
In this appendix, we present a very useful approximation formula: for a large enough M and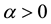

It is easy to see that 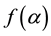

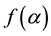
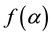
Numerically, we computed the values of


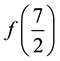
very good approximation.