Received 21 October 2014; revised 16 November 2014; accepted 11 December 2014

ABSTRACT

In present paper we prove the local well-posedness for Von Neumann-Landau wave equation by the T. Kato’s method.

Keywords:

Von Neumann-Landau Wave Equation, Strichartz Estimate, Cauchy Problem

1. Introduction

For the stationary Von Neumann-Landau wave equation, Chen investigated the Dirichlet problems [1] , where the generalized solution is studied by Function-analytic method. The present paper is related to the Cauchy problem: the Von Neumann-Landau wave equation

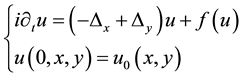, (1)

where 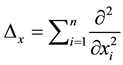for 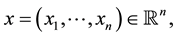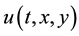is an unknown complex valued function on 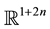and is a nonlinear complex valued function.

If the plus “+” is replaced by the minus “−” on right hand in Equation (1), then the resulted equation is the Schrödinger equation. For the Schrödinger equation, the well-posedness problem is investigated for various nonlinear terms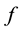. In terms of the nonlinear terms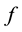, the problem (1) can be divided into the subcritical case and the critical case for 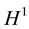solutions. We are concerned with the subcritical case and obtain a local well- posedness result by the T. Kato’s method.

The paper is organized as follows. Section 2 contains the list of assumptions on the interaction term 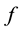and the main result is presented. Section 3 is concerned with the Strichartz estimates. Finally, in Section 4, the main result is proved.

2. Statement of the Main Result

In this section we list the assumptions on the interaction term 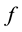and state the main result. Firstly, we recall that the definition of admissible pair [2] .

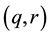Definition 2.1. Fix,. We say that a pair of exponents is admissible if

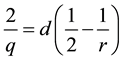, (2)

and

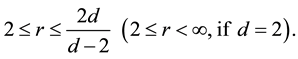(3)

Remark 2.1. The pairs is always admissible, so is the if The two pairs are called the endpoint cases.

Secondly, let satisfy

, (4)

and

, (5)

for all such that with

(6)

where is a constant independent of Set

, (7)

for all measurable function and a.e..

Finally, let us make the notion of solution more precise.

Definition 2.2. Let be an interval such that We say that is a strong -solution of (1) on if satisfies the integral equation

, (8)

for all where

The main result is the following theorem:

Theorem 1. Suppose Let satisfy (4)-(6). If (considered as a function) is of class, then the Cauchy problem (1) is locally well posed in More specially, the following properties hold:

(i) For any there exists a time and constant such that for each in the ball there exists a unique strong -solution to the Equation (1) in such that

(9)

where and is an admissible pair.

(ii) The map is continuous from to

(iii) For every the unique solution is defined on a maximal interval with and

(iv) There is the blowup alternative: If then as (respectively, if then as).

Remark 2.2. It follows from Strichartz estimates that

,

for any admissible pair

Remark 2.3. For the Schrödinger equations, the similar results hold [2] . It implies a fact that the ellipticity of the operator is not the key point in the local well-posedness problem.

3. Strichartz Estimates

In this subsection, we recall that the Strichartz estimates. Let denote a general Fourier variable in Let then by Fourier transform(denoting by or) we have

, (10)

for any It is easy to verify that the is a self-adjoint unbounded operator on with the domain Then, by Stone theorem we see that is an unitary group on. Moreover,

can be expressed explicitly by Fourier transform.

, (11)

for any By the direct compute, we conclude

(12)

The following result is the fundamental estimate for

Lemma 1. If and then maps continuously to and

(13)

where is the dual exponent of defined by the formula

Proof. For the proof please see [3] or [4] . □

The following estimates, known as Strichartz estimates, are key points in the method introduced by T. Kato [5] .

Lemma 2. Let and be any admissible exponents. Then, we have the homogeneous Strichartz estimate

(14)

the dual homogeneous Strichartz estimate

(15)

and the inhomogeneous Strichartz estimate

, (16)

for any interval and real number

Proof. For the proof please see [3] or [4] in the non-endpoint case. On the other hand, the proof in the endpoint case follows from the theorem 1.2 in [6] and the lemma 1 in the present paper. □

4. The Proof of Theorem

Proof. Let be such that for and for Setting

one easily verifies that for any

(17)

Set for Using (17), we deduce from Hölder’s inequality that

(18)

And it follows from Remark 1.3.1 (vii) in [2] that

(19)

We now proceed in four steps.

Step 1. Proof of (i). Fix to be chosen later, and let, be such that is an ad- missible pair, and set Consider the set

, (20)

equipped with the distance

(21)

We claim that is a complete metric space. Indeed, let be a Cauchy sequence. Clearly, is also a Cauchy sequence in and In particular, there exists a function such that in and as

Applying theorem 1.2.5 in [2] twice, we conclude that

,

and that

thus, in as

Taking up any Since is continuous it follows that is measurable, and we deduce easily that Similarly, since is continuous we see that Using inequalities (18) and (19) and Remark

1.2.2 (iii) in [2] , We deduce the following:

and

Using the embedding and Hölder’s inequality in time, we deduce from the above estimates that

, (22)

and

(23)

Given. For any let be defined by

(24)

It follows from (22) and Strichartz estimates (lemma 2) that

(25)

and

(26)

Also, we deduce from (23) that

(27)

Finally, note that We now proceed as follows. For any we set and we let be the unique positive number so that

(28)

It then follows from (26) and (28) that for any

(29)

Thus, and by (27) we obtain

(30)

In particular, is a strict contraction on By Banach’s fixed-point theorem, has a unique fixed

point that is satisfies (8). By (25),. By the definition 2.2, we con- clude that is a strong -solution of (1) on Note that is decreasing on, then the estimate (9) holds for by letting in (29).

For uniqueness, assume that are two strong -solution of (1) on with the same initial value. Then, we have

(31)

For simplicity, we set

,

for and For any interval by (18) and Strichartz estimates (16), then we obtain

(32)

Similarly, for we have

(33)

Note that Then, it follows from that

, (34)

where the constant and the constant is independent of by above inequalities. Note that we conclude that by the lemma 4.2.2 in [2] . So

Step 2. Proof of (ii). Suppose that in as By the part (i), we denote and by

the unique solution of (1) corresponding to the initial value and, respectively. We will show that in as Note that

(35)

and the estimate (29) which implies that (27) holds for Note that the choosing of the time in (28), it follows from (27) with (30) that

(36)

Hence, we have

(37)

Next, we need to estimate Note that commutes with, and so

(38)

A similar identity holds for We use the assumption which implies that where is a real matrix. Therefore, we may write

(39)

Note that and are also so that and from (17) we deduce that and for any and some constant Therefore, arguing as in Step 1, we obtain the estimate

(40)

By choosing as (28) and noting that from (40) we obtain that

(41)

There, if we prove that

, (42)

as then we have

, (43)

as which, combined with (37), yields the desired convergence. we prove (42) by contradiction, and we assume that there exists and a subsequence, which we still denote by such that

(44)

By using (37) and possibly extracting a subsequence, we may assume that a.e. on and that there exists such that a.e. on In particular, both and converge to 0 a.e. on Since

and

we obtain from the dominated convergence a contradiction with (44).

Step 3. Proof of (iii). Consider and let

It follows from part (i) there exists a solution

,

of (1).

Step 4. Proof of (iv). Suppose now that and assume that there exist and a sequence such that Let be such that By part (i), from the initial data one can extend up to, which contradicts maximality. Therefore,

One shows by the same argument that if then

This completes the proof. □

Acknowledegments

We are grateful to the anonymous referee for many helpful comments and suggestions, which have been incorporated into this version of the paper. C. Liu was supported in part by the NSFC under Grants No. 11101171, 11071095 and the Fundamental Research Funds for the Central Universities. And M. Liu was supported by science research foundation of Wuhan Institute of Technology under grants No. k201422.

References