Journal of Applied Mathematics and Physics
Vol.2 No.8(2014), Article
ID:47945,5
pages
DOI:10.4236/jamp.2014.28091
Simplified Homogeneous Balance Method and Its Applications to the Whitham-Broer-Kaup Model Equations
Mingliang Wang1,2, Xiangzheng Li1
1School of Mathematics & Statistics, Henan University of Science & Technology, Luoyang, China
2Department of Mathematics, Lanzhou University, Lanzhou, China
Email: mlwang@haust.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 June 2014; revised 3 July 2014; accepted 11 July 2014
ABSTRACT
A nonlinear transformation of the Whitham-Broer-Kaup (WBK) model equations in the shallow water small-amplitude regime is derived by using a simplified homogeneous balance method. The WBK model equations are linearized under the nonlinear transformation. Various exact solutions of the WBK model equations are obtained via the nonlinear transformation with the aid of solutions for the linear equation.
Keywords:WBK Model Equations, Simplified Homogeneous Balance Method, Nonlinear Transformation, Multiple Soliton Solutions, Periodic Solutions in Space Variable, Rational Solutions

1. Introduction
The Whitham-Broer-Kaup model equations (WBK) [1] -[5] in the shallow water small-amplitude regime are that
 (1)
(1)
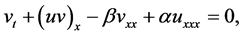 (2)
(2)
where  represents the horizontal velocity, and
represents the horizontal velocity, and  the height deviated from the equilibrium position of the liquid,
the height deviated from the equilibrium position of the liquid, 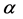 and
and  are constants. The WBK models (1) and (2) are very good models to describe dispersive waves. If
are constants. The WBK models (1) and (2) are very good models to describe dispersive waves. If 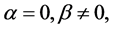 Equations (1) and (2) describe a shallow water waves with diffusion; if
Equations (1) and (2) describe a shallow water waves with diffusion; if 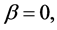
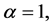 Equations (1) and (2) become the variant Boussinesq equations. In the latest paper [6] , the multiple soliton solutions of Equations (1) and (2) have been obtained by using the simplified form of Hirota’s direct method.
Equations (1) and (2) become the variant Boussinesq equations. In the latest paper [6] , the multiple soliton solutions of Equations (1) and (2) have been obtained by using the simplified form of Hirota’s direct method.
In the present paper, we will apply a simplified homogeneous balance method to investigate the WBK model Equations (1) and (2), by this method a nonlinear transformation that from the solution for a linear equation to the solution for the WBK model equations is derived, and more type of solutions than those given in [6] are obtained via the nonlinear transformation successfully.
2. Derivation of the Nonlinear Transformation
Considering the homogeneous balance between 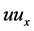 and
and 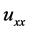 in Equation (1), and between
in Equation (1), and between 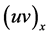 and
and 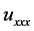 in Equation (2) (2m + 1 = m + 2, m + n + 1= m + 3, which implies that m = 1, n = 2), we can suppose that the solution of Equations (1) and (2) is of the form
in Equation (2) (2m + 1 = m + 2, m + n + 1= m + 3, which implies that m = 1, n = 2), we can suppose that the solution of Equations (1) and (2) is of the form
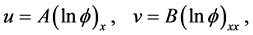 (3)
(3)
where we use  and
and 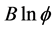 instead of the undetermined functions
instead of the undetermined functions 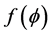 and
and 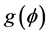 appearing in the original homogeneous balance method (HB) [7] -[9] to simplify the original HB, constants
appearing in the original homogeneous balance method (HB) [7] -[9] to simplify the original HB, constants  and
and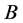 , and the function
, and the function 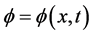 are to be determined later. The aim of the simplified HB is to find
are to be determined later. The aim of the simplified HB is to find 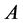 and
and , and the function
, and the function  such that the expressions (3) exactly satisfies Equations (1) and (2).
such that the expressions (3) exactly satisfies Equations (1) and (2).
Substituting (3) into the left hand sides of Equations (1) and (2), yields
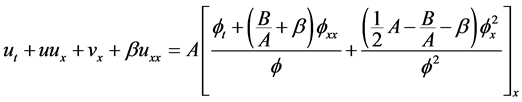 (4-1)
(4-1)
 (4-2)
(4-2)
In order to determine  and
and , we set the coefficients of the terms with
, we set the coefficients of the terms with  appearing in expressions (4) to zero, yields algebraic equations for
appearing in expressions (4) to zero, yields algebraic equations for  and
and 
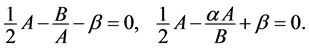 (5)
(5)
Solving the algebraic equations we have
 (6)
(6)
Substituting (6) into (3), yields
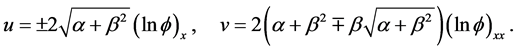 (7)
(7)
Using (5) and (6), the expressions (4) become
 (8-1)
(8-1)
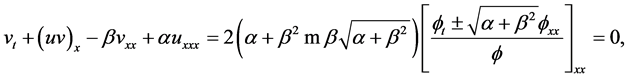 (8-2)
(8-2)
provided that the function 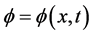 satisfies the linear equation
satisfies the linear equation
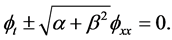 (9)
(9)
Based upon (7), (8) and (9), we come to the conclusion that inserting each solution of the linear equation (9) into (7), we can obtain the exact solution of the WBK model Equations (1) and (2), and the expressions (7) with linear Equation (9) can be looked upon as a nonlinear transformation that from the solution for linear Equation (9) to the solution for WBK model Equations (1) and (2), because every solution of linear Equation (9) under (7) is transformed into the solution of the WBK model Equations (1) and (2), therefore the WBK model Equations (1) and (2) can be linearized by the linear Equation (9), according to [10] , the WBK model equations are C-integrable equations.
3. Exact Solutions of the WBK Model Equations
According to the superposition principle for a linear problem, the linear Equation (9) can admit many solutions, for example,
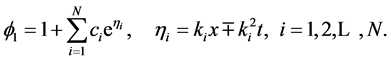 (10)
(10)
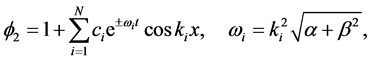 (11)
(11)
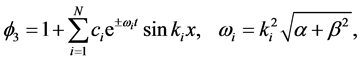 (12)
(12)
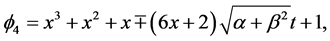 (13)
(13)
and so on., where integer ,
, 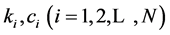 are constants.
are constants.
Substituting (10) into (7), we have the multiple soliton solutions of the WBK model Equations (1) and (2) as follows
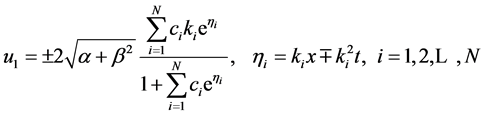 (14-1)
(14-1)
 (14-2)
(14-2)
If 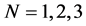 the expressions (14) become the 1—soliton solutions, 2—solliton solutions and 3—soliton solutions for the WBK model equations, respectively, these results coincide with those obtained by using the simplified form of Hirota’s method in [6] one by one. In particular, when
the expressions (14) become the 1—soliton solutions, 2—solliton solutions and 3—soliton solutions for the WBK model equations, respectively, these results coincide with those obtained by using the simplified form of Hirota’s method in [6] one by one. In particular, when , (14) becomes
, (14) becomes
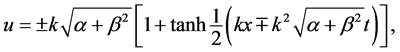
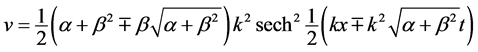 where
where 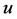 represents a single kink solitary wave, and
represents a single kink solitary wave, and ![]() a single bell solitary wave of the WBK model Equations (1) and (2).
a single bell solitary wave of the WBK model Equations (1) and (2).
Substituting (11) into (7), we have the periodic solutions in space variable 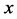 for the WBK model Equations (1) and (2)
for the WBK model Equations (1) and (2)
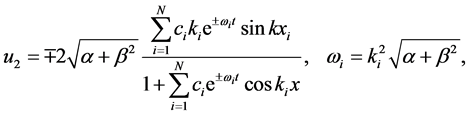
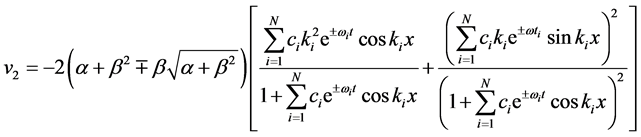 .
.
Similarly, substituting (12) into (7), we also have the periodic solutions in space variable 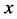 for the WBK model Equations (1) and (2)
for the WBK model Equations (1) and (2)

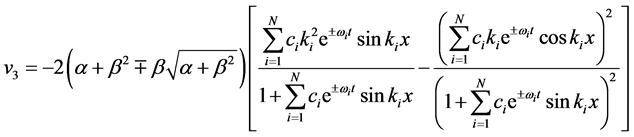 .
.
Substituting (13) into (7), we have rational solutions for the WBK model Equations (1) and (2)
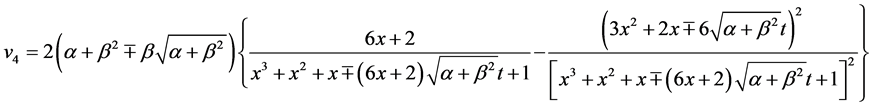

We point out that the solutions  to the WBK model equations have not appeared in [6] .
to the WBK model equations have not appeared in [6] .
4. Conclusion
In this paper, the original HB is simplified by using a logarithmic function instead of the undetermined function appearing in the original HB. The nonlinear transformation that from the solution for the linear equation to the solution for the WBK model equation is derived by using the simplified HB. The WBK model equations are linearized under the nonlinear transformation. The multiple soliton solutions, periodic solutions in space variable and rational solutions of the WBK model equations are obtained in terms of solutions for the linear equation.
Acknowledgements
This work is supported in part by the Natural Science Foundation of Education Department of Henan Province of China (Grant No. 2011B110013, 12B110006) and the Doctoral Foundation of Henan University of Science and Technology (Grant No. 09001562).
References
- Whitham, G.B. (1967) Variational Methods and Applications to Water Waves. Proceedings of the Royal Society A, 299, 6-25. http://dx.doi.org/10.1098/rspa.1967.0119
- Broer, L.J. (1975) Approximate Equations for Long Water Waves. Applied Scientific Research, 31, 377-395. http://dx.doi.org/10.1007/BF00418048
- Kaup, D.J. (1975) A Higher-Order Water-Wave Equation and the Method for Solving It. Progress of Theoretical Physics, 54, 396-408. http://dx.doi.org/10.1143/PTP.54.396
- Kupershmidt, B.A. (1985) Mathematics of Dispersive Waves. Communications in Mathematical Physics, 99, 51-73. http://dx.doi.org/10.1007/BF01466593
- Fan, E. and Zhang, H. (1998) Backlund Transformation and Exact Solutions for Whitham-Broer-Kaup Equations in Shallow Water. Applied Mathematics and Mechanics, 19, 713-716. http://dx.doi.org/10.1007/BF02457745
- Wazwaz, A.M. (2013) Multiple Soliton Solutions for the Whitham-Broer-Kaup Model in Shallow Water Small-Amplitude Regime. Physica Scripta, 88. http://dx.doi.org/10.1088/0031-8949/88/03/035007
- Wang , M.L. (1995) Solitary Wave Solutions for Variant Boussinesq Equations. Physics Letters A, 199, 169-172. http://dx.doi.org/10.1016/0375-9601(95)00092-H
- Wang, M.L. (1996) Exact Solutions for a Compound KdV-Burgers Equation. Physics Letters A, 213, 279-287. http://dx.doi.org/10.1016/0375-9601(96)00103-X
- Wang , M.L., Zhou, Y.B. and Li, Z.B. (1996) Application of a Homogeneous Balance Method to Exact Solutions of Nonlinear Equations in Mathematical Physics. Physics Letters A, 216, 67-75. http://dx.doi.org/10.1016/0375-9601(96)00283-6
- Calogero, F. (1991) Springer Series in Nonlinear Dynamics. Zakharov, V.E., Ed., Springer, Berlin, 1-62.

