Journal of Applied Mathematics and Physics
Vol.02 No.07(2014), Article ID:46848,5 pages
10.4236/jamp.2014.27065
The Modified Kadomtsev-Petviashvili Equation with binary Bell polynomials
Ningning Hu, Shufang Deng*
Department of Mathematics, East China University of Science and Technology, Shanghai, China
Email: *sfangd@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 February 2014; revised 20 March 2014; accepted 27 March 2014
ABSTRACT
Binary Bell Polynomials play an important role in the characterization of bilinear equation. The bilinear form, bilinear Bäcklund transformation and Lax pairs for the modified Kadomtsev-Pet- viashvili equation are derived from the Binary Bell Polynomials.
Keywords:
Binary Bell Polynomials, Bilinear Bäcklund transformation, Lax pair

1. Introduction
There are some techniques that can be used to solve the nonlinear evolution equations, such as inverse scattering transformation, Hirota method, Darboux transformation and the tanh method [1] -[4] . Among this methods, the bilinear method and bilinear Bäcklund transformation have proved particularly powerful. Through the dependent variable transformations, some nonlinear evolution equations can be transformed into bilinear forms. Applying the bilinear method developed by Hirota, we can obtian the soliton solutions and quasiperiodic wave solutions [5] - [7] . The construction of the bilinear Bäcklund transformation [8] by using Hirota method relies on a par- ticular skill in using appropriate exchange formulas which are connected with the linear presentation of the system. Yet, the construction of bilinear Bäcklund transformation is complicated. Recently, Lambert, Gilson et al. [9] - [11] proposed an alternative procedure based on the use of the Bell polynomials which enabled one to obtain parameter families of bilinear Bäcklund transformation and Lax pairs for the soliton equations in a lucid and systematic way. In Ref [12] , Fan has constructed bilinear formalism, bilinear Bäcklund transformation, Lax pairs and infinite conservation laws for the nonisospectral and variable-coefficient KdV equation.
In this paper, we will extend the Binary Bell polynomials to deal with the modified Kadomtsev-Petviashvili (mKP) equation. First, we derive the bilinear form for the mKP equation by the binary Bell polynomials. Second, the bilinear Bäcklund transformation and Lax pairs are obtained in a quick and natural manner.
2. The Bilinear Form for the mKP equation
The mail tool used here is a class of generalized multi-dimensional binary Bell polynomials. First, we give some notations on the Bell polynomials to easily understand our presentation.
Lambert et al. proposed a generalization of the Bell polynomial [9] - [11] . Let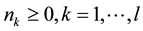 , denote arbitrary integers,
, denote arbitrary integers, 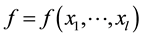 be a
be a 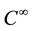 multi-variable function, the following polynomials
multi-variable function, the following polynomials
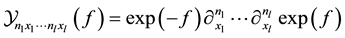 (1)
(1)
is called multi-dimensional Bell polynomial (generalized Bell polynomial or Y-polynomials). If all partial
derivatives  are taken as different variable elements, then the
are taken as different variable elements, then the
generalized Bell polynomial 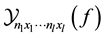 is the multivariable polynomial with respect to these variable
is the multivariable polynomial with respect to these variable
elements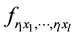 . The subscripts in the notation
. The subscripts in the notation 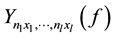 denote the highest order derivatives of
denote the highest order derivatives of 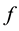
with respect to the variable 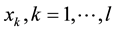 respectively.
respectively.
For the special case , the associated two-dimensional Bell polynomials defined by (1) read
, the associated two-dimensional Bell polynomials defined by (1) read
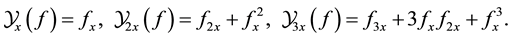 (2)
(2)
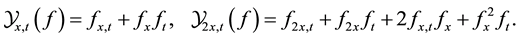 (3)
(3)
Base on the use of above Bell polynomials (1), the multidimensional binary Bell polynomials (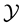 -poly- nomials) can be defined as follows
-poly- nomials) can be defined as follows
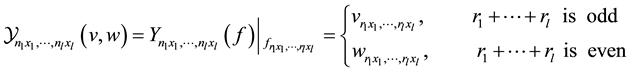 (4)
(4)
which is a multivariable polynomials with respect to all partial derivatives 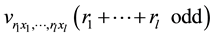 and
and
The binary Bell polynomials also inherits the easily recognizable partial structure of the Bell polynomials. The lowest order binary Bell polynomials are


The link between binary Bell polynomials 


in which


In the particular case when

in which the P-polynomials can be characterized by an equally recognizable even part partitional structure

The formulaes (7),(9) and (10) will prove particular useful in connecting nonlinear equations with their corresponding bilinear equations. This means that once a nonlinear equation is expressible as a linear combi- nation of the P-polynomials, then it can be transformed into a linear equation.
The binary Bell polynomials 

The key property of the multi-dimensional Bell polynomials

implies that the binary Bell polynomials 
transformation


The formulaes (11) and (13) will then provide the shortest way to the associated Lax system of nonlinear equations.
In this paper we consider the mKP equation

Let a potential field 

Substituting (15) into (14), we have

Introducing two new variables

using the binary Bell polynomials (5) and (6),equation (16) can be written into

A possible choice of such constraint maybe

then

Substituting (20) into (18) and using the relation (19), we have

Therefore, from (19) and (21), we deduce a couple system of 


By application of the identity (7) and the transformation (17), equations (22) and (23) lead to the bilinear form for the mKP equation


Using Hirota's bilinear method, it is easy to solve the multisoliton solutions for the mKP equation. For example, the one-soliton solution reads

where 

3. Thebilinear Bäcklund Transformation and Lax pairs for the mKP equation
In this section, we consider the bilinear Bäcklund transformation and Lax pair for the mKP equation.
Set

be two different solutions of (16), respectively. We associate the two-field condition

By the relation


Equation (28) can be transformed into

Let




so Equation (31) becomes

Similar to the (21), by the relation


Equation (36) can be transformed into

Then from (27) to (39), we get the system of 






Using the link between Bell Polynomials and Hirota bilinear bilinear Bäcklund transformation (7), the bilinear Bäcklund transformation can be written as






Through the bilinear Bäcklund transformation, we can get the soliton solutions for the mKP equation.
In the following, we will give the Lax pair for the mKP equation. By transformations

and the relation (13), the formulaes (48) and (50) become


Set

then 



which is the Lax pair of the mKP equation.
Similar to the (56) and (57). Let


Let




which is the Lax pair for the mKP equation.
4. Conclusion
Binary Bell Polynomials play an important role in the characterization of bilinear equation. By the Binary Bell Polynomials, we give the bilinear form, bilinear Bäcklund transformation and Lax pairs for the modified Kadomtsev-Petviashvili equation. This method is a lucid and systematic way. This method can be extended to the other soliton equations.
Acknowledgments
The work is supported by the National Natural Science Foundation of China (11301183).
References
- Ablowitz, M.J. and Clarkson, P.A. (1991) Solitons, Non-linear Evolution Equations and Inverse Scattering Transform. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511623998
- Hirota, R. (1971) Exact Solution of the Korteweg-de Vries Equation Formultip le Collisions of Colitons. Physical Re- view Letters, 27, 1192-1194. http://dx.doi.org/10.1103/PhysRevLett.27.1192
- Matveev, V.B. and Salle, M.A. (1991) Darboux Transformations and Solitons. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-00922-2
- Fan, E.G. (2000) Extended Tank-Function Method and Its Applications to Nonlinear Equations. Physics Letters A, 277, 212-218. http://dx.doi.org/10.1016/S0375-9601(00)00725-8
- Hu, X.B., Lou, S.Y. and Qian, X.M. (2009) Nonlocal Symmetries for Bilinear Equations and Their Applications. Stu- dies in Applied Mathematics, 122, 305-324. http://dx.doi.org/10.1111/j.1467-9590.2009.00435.x
- Fan, E.G. and Hon, Y.C. (2008) Quasiperiodic Waves and Asymptotic Behavior for Bogoyvlenskii’s Breaking Soliton Equation in (2 + 1) Dimensions. Phyical Review E, 78, Article ID: 036607. http://dx.doi.org/10.1103/PhysRevE.78.036607
- Fan, E.G. (2009) Quasi-Periodic Waves and Wsymptotic Property for the Asymmetrical Nizhnik-Novikov-Veselov Equation. Journal of Physics A Mathematical and Theoretical, 42, Article ID: 095206. http://dx.doi.org/10.1088/1751-8113/42/9/095206
- Hirota, R. (1974) A New Form of Backlund Transformations and Its Relation to the Inverse Scattering Problem. Pro- gress of Theoretical Physics, 52, 1498-1512. http://dx.doi.org/10.1143/PTP.52.1498
- Gilson, C., Lambert, F., Nimmo, J. and Willox, R. (1996) On the Combinatoricd of the Hirota D-Operators. Proceed- ings the Royal of Society A, 452, 223-234. http://dx.doi.org/10.1098/rspa.1996.0013
- Lambert, F., Loris, I. and Springael, J. (2001) Classical Darboux Transformations and the KP Hierarchy. Inverse Problems, 17, 1067-1074. http://dx.doi.org/10.1088/0266-5611/17/4/333
- Lambert, F. and Springael, J. (2008) Soliton Equations and Simple Combinatorics. Acta Applicandae Mathematicae, 102, 147-178. http://dx.doi.org/10.1007/s10440-008-9209-3
- Fan, E.G. (2011) The Integrability of Nonisospectral and Variable-coefficient KdV Equation with Binary Bell Poly- nomials. Physics Letters A, 375, 493-497.
NOTES
*Corresponding author.



