Advances in Physical Education
Vol.07 No.03(2017), Article ID:78566,11 pages
10.4236/ape.2017.73028
State Transition Probability as the Anticipation Clue of the Course of a Struck Ball
Toshimi Kudo1, Yuji Yamamoto2, Hidenori Shinohara3, Riko Kudo4
1Department of Psychological and Behavioral Science, Miyagi Gakuin Women’s University, Sendai, Japan
2Research Center of Health, Physical Fitness, and Sports, Nagoya University, Nagoya, Japan
3Department of Education, Miyagi Gakuin Women’s University, Sendai, Japan
4Graduate School of Education and Human Development, Nagoya University, Nagoya, Japan

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 19, 2017; Accepted: August 15, 2017; Published: August 18, 2017
ABSTRACT
When opponent players in a racket competition anticipate the course of a struck ball, they use the kinematic clues when the ball is struck as clues, including various contextual informations, such as the position when the ball is struck and the status of the game. This study proposes a measurement method of the state transition probability that shows the connection between two strokes as effective contextual information for increasing the accuracy of a player’s anticipation of the course of a struck ball. The state transition probability that is calculated by the proposed method shows the struck ball sequence pattern for a player, and whether characteristic differences can be found between players is examined. Two matches of opposing players in a soft tennis singles match competition were analyzed in this study. The two-dimensional actual coordinate data of the drop position of the ball was acquired from the target matches. The courts were divided into three sections from the left to right direction, the depth direction, and from the net towards the baseline. The striking of the ball within these sections was defined as one state, and the state transition probability matrix was measured. The result shows that the state transition probabilities of two players, namely, the characteristic differences in the struck ball sequence pattern, were observed, and their effectiveness as contextual information of the prediction clues was demonstrated.
Keywords:
State Transition Probability, Anticipation Clue, Contextual Information, Tennis

1. Introduction
In ball games and net-type interpersonal competitions, players must anticipate the moves of opponents and their team members and the changes in the environment. They must take appropriate action in response to various circumstances arising in a match (Abernethy, 1990; Jackson et al., 2006; Savelsbergh et al., 2002) . For example, in a tennis singles match, a player anticipates the opponent’s position, the course of the struck ball, the skill (forehand, backhand) and ball type (drop shot, top spin) appropriately while considering the status of the game and the count, and determines the strategy to adopt and executes the corresponding action.
Many previous anticipation studies have focused on the anticipation clues that are needed for accurate decision-making. Efforts have been devoted to specifying the body parts that serve as clues for prediction from gaze point devices, such as Gaze Movement or EyeTracker, or finding kinematic clues from a temporal occlusion paradigm (Williams et al., 2002) . Recently, it has become clear that the anticipations are not made based on local sensory information processing that employs single kinematic clues (Williams et al., 2009) , but are rather established by global and dynamic integrative sensory information processing (Smeeton et al., 2011; Huys et al., 2009; Bourne et al., 2011) .
Although these series of studies have exhibited certain results with a view towards the elucidation of the predictive mechanism, these results cannot be claimed that the research results are being fully utilized at points of instruction. Williams et al. (2002) have shown that the slow replay presentation of video accompanied by verbal instruction can contribute to raising the predictive ability of beginner tennis players, but the effectiveness of the verbal instruction and video presentations has not been fully verified in many other studies. This is because even if a player has participated in the experiments of a cognitive training program for raising the predictive abilities, the control of the conditions is difficult; therefore, the direct effects of training cannot be verified (Williams et al. 2004) .
When the anticipation mechanisms occurring at tennis competitions are considered, coaches and guides know empirically that a player uses the contextual information, such as the opponent’s position, to anticipate the course of a struck ball. As reported by Loffing and Hagemann (2014) , the anticipation information processing of beginners, who have not yet acquired the expertise peculiar to tennis, depends only on kinematic clues; therefore, their predictive accuracy is inferior. However, skilled players can limit to a fixed range the potential range of a struck ball from the opponent’s position based on experience that they have acquired in the course of mastering the sport, and when kinematic clues are provided, they can further narrow the course from the limited struck ball courses. Specifically, we can state that the predictive behavior of a skilled player does not involve information processing based on kinematic information, but rather global and dynamic integrative information processing that also includes contextual information that uses the player’s position as a clue. To examine this contextual information, the relationship between a player’s position and the course of a struck ball can be obtained by tracking the drop position of the ball and measuring the discrete probability variable  of the number of struck balls that drop in a preset court division
of the number of struck balls that drop in a preset court division 
 . Specifically, when a certain player hits a ball from a certain position, it is possible to learn the probability of which struck ball course is common, which then becomes the information that increases a player’s predictive accuracy (Figure 1(a)).
. Specifically, when a certain player hits a ball from a certain position, it is possible to learn the probability of which struck ball course is common, which then becomes the information that increases a player’s predictive accuracy (Figure 1(a)).
While a player is subject to restrictions due to his/her position when a ball is struck, which forms the basis of the struck ball course, the struck ball course is determined based on the pre-planned struck ball sequence pattern. For example, in a situation where “a player hits a ball delivered by a forehand stroke by the opponent, and the next struck ball that is returned is a backhand stroke”, a player can form an image beforehand of the struck ball sequence pattern for the next two or three strokes. In actual competition, a player will make corrections to the struck ball sequence pattern while observing his/her opponent’s position, and ultimately decides the course of the struck ball. Therefore, we can conclude that the information related to the relationship of the struck ball course that expresses the characteristics of a struck ball sequence pattern is useful for raising a player’s predictive accuracy in a competition. The state transition probability, which grasps the struck ball course as one state, is obtained by applying the Markov process to the continuously changing struck ball course. If this informa-

Figure 1. Type of anticipation based on context information. Panel (a) shows that player A anticipates the struck ball course using player B’s hitting position as a cue. Panel (b) shows that player A anticipates the course represented by the solid line with the struck ball course represented by the dotted line as a cue.
tion is provided in advance to a player, the potential range of a struck ball from the opponent can be limited considerably, and it is anticipated that the predictive accuracy will increase (Figure 1(b)).
Presently, in game analysis related research beginning with anticipation studies, majority of the studies that deal with state transition probability are either related to the points scored and the variety of struck balls and skills when a ball is struck (Abernethy & Russell, 1987; Abernethy, 1990; McGarry & Franks, 1994; McGarry & Franks, 1996; Wong & Zigarovich, 2007) or the cognitive processing by the competitors (Gray, 2002) . There are almost no studies that deal with the state transition probability of the course of a struck ball. Among the latter, Pfeiffer et al. (2010) have examined the association between the state transition probability of the course of a struck ball and points scored in table tennis competition, but no relationship has been found. The points scored in net-type competitions, such as table tennis and tennis, are affected by the effectiveness in striking the ball. If the ball is effectively struck, the probability of scoring points increases, otherwise, this is likely tied to losing a point. It is believed that the state transition of the course of a struck ball or the type of shot shows the struck ball sequence pattern for a player and may not be directly connected to winning or losing a point. We can tentatively conclude that this matter is a key factor that has no correlation between the state transition of the course of a struck ball or the type of shot and the performance.
In this study, a method whereby the state transition probability of a struck ball course is measured with actual data. However, similar to the case of Pfeiffer et al. (2010) , the present study does not mention the relationship with points scored, and its purpose is to examine whether or not the characteristics of a player’s struck ball sequence pattern can be depicted from the state transition probability that is measured with the proposed method.
2. Application of the Markov Process Pertaining to Struck Ball Course Analysis
If we assume that the course of a struck ball at a certain time point t is taken as one state st, and the course of the next struck ball in response to the returned ball is state st+1, it can be stated that the player is engaging in preplanned continuous decision-making that transitions state st to state st+1. If the transition probability from the state st and state st+1 is set at p(st, st+1), and this expresses a characteristic tendency in each player, this can become an extremely effective information in terms of raising a player’s predictive accuracy. Here, several patterns that are necessary to measure the transition state probability are defined in advance.
The number of states m when the court is divided into d divisions can be defined as m = d. Moreover, assuming that one struck ball of each player within 1 point is set as r, the Sr of the number r rally is defined as follows.
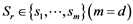
Therefore, the state transition probability matrix of the struck ball course can be defined as follows.
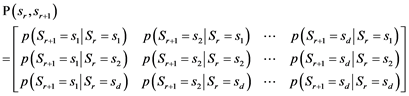
3. State Transition Probability Based on Actual Data
3.1. Method
3.1.1. Analysis of the Subject
The same two players who competed in a singles match of the male national tournament finals and the male individual match singles finals at the 7th Asian Soft Tennis Championship Meet held in Jiayi City (Republic of China) on July 14 to 21, 2012 were used as subjects. They are both right-handed. This study targeted the winners of individual and team events in order to determine the trend shown by the top-seeded players. Soft tennis is a type of tennis that was developed in Japan based on hard tennis. The main difference between soft tennis and hard tennis is that soft rubber balls are used in former compared to hard rubber balls in the latter; therefore, it is called “soft tennis”. Soft tennis is popular in Japan as a sport that can be enjoyed by a wide range of age group regardless of their sex. About 540,000 people participate in the soft tennis competition (http://www.jsta.or.jp/wp-content/uploads/international/en/).
The approval of the Japan Soft Tennis Association has been obtained for the use of the video that was used in this study.
3.1.2. Imaging Method
A digital video camera was installed at approximately 15 m to the rear of the front baseline of the court and at a height of approximately 4 m from the court surface. The zoom was adjusted so that the front baseline could be captured and video was recorded.
3.1.3. Acquisition of Actual Data
Among the points of the two matches, the rallies that continued for at least four strokes were used for analysis, and the rallies of three or fewer strokes were excluded. Furthermore, the rallies where the struck ball resulted in an error were also excluded.
The recorded video images were imported into a PC (screen resolution 720 × 480), and the drop positions of the balls struck by the two athletes were digitized at 30 Hz. Then, the actual coordinate data was measured using the two-dimen- sional Direct Linear Transform method (Abdel-Aziz & Karara, 2015) . This coordinate system is shown in Figure 2.
In soft tennis matches, the changing of sides is done after the odd numbered games are finished. Therefore, the coordinate conversion was performed for the coordinate position at which the ball was struck from the backcourt (far side) to the coordinate position at which the ball was struck from the forecourt side (near side).
Figure 2. Coordinate system used in this study. Near side means closer to the video camera.
3.1.4. State Transition Analysis
In a competition, when a player anticipates the course of a struck ball, this is not done in accordance with the subdivision of the court. However, it is inferred that the player is determining whether to use a forehand or backhand stroke or whether to drive the ball or try a drop shot. Accordingly, in this study, the court was divided into three sections for the horizontal direction and the depth direction, and from the net towards the baseline (Figure 3(a) and Figure 3(b)).
For one stroke for each point, the state in which the struck ball course that was divided into three sections in the horizontal direction was set as W (width), and the state in which the struck ball course that was divided into three sections in the depth direction was set as D (depth). Therefore, state W transitions in state , and state D transitions in state
, and state D transitions in state .
.
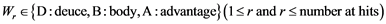
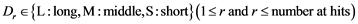
Therefore, for each point, when the number of strokes from the initial stroke (the third stroke on the service side) until the point is dead is set as r, the state Wr and the state Dr and the state transition probability matrices PW,A, PW,B, PD,A and PD,B can be defined as follows. The initial number of strokes on the service side was set at 1.

Figure 3. State divided into three. Panel (a) shows the W state; Panel (b) shows the D state.
3.1.5. Statistical Analysis
A Fisher’s exact test (with n × m contingency table version 1.3, MATLAB R2016a) was performed for each state of state W and state D in order to verify whether the state transition probabilities measured between the two players are independent.
3.2. Results
The frequency of transitioning from Wr to Wr+1 was measured with a breakdown by players A and B with the x coordinate for the horizontal direction from the two-dimensional coordinate data (xr, yr) in each rally of the two matches (Figure 4(a)). Similarly, the frequency of transitioning from Dr to Dr+1 was measured with a breakdown by player with the y coordinate for the depth direction (Figure 4(b)).
Next, the state transition probability matrices PW,A, PW,B, PD,A and PD,B for the state W and state D by player were calculated from the obtained frequency (Figures 5(a)-(d)).
The result of the Fisher’s exact test shows that the null hypothesis was rejected for all states [state W (p = 0.3333), state D (p = 0.1667)]. The state transition probability was confirmed to be independent of the two players, and a difference was also observed.
3.3. Discussion
The results in this study show that the characteristics of the struck ball sequence pattern similar to those indicated below can be observed. The p(A|A) of player A is larger than that of player B, and many connections from state A to state A can be observed (Figure 5(a)). When player A strikes the ball in state A, player B may narrow down the struck ball course with the focus on state A. Meanwhile, given that player B is distributing the ball evenly in state A, state D and state B


Figure 4. Frequency of state transitions on each player. Panel (a) shows the state transitions in the horizontal direction (W). Panel (b) shows the state transitions in the depth direction (D). Red bars show player A and blue bars show player B. And arrows in the figure indicate that the state transited one state to another.
can be cited as characteristics (Figure 5(b)). Moreover, when the state transition probability p(S|L) from state L to state S of both players is compared, the characteristic that can be cited is 0.20 for player A. Comparatively, there is a transition from state L to state S (Figure 5(c)), where it is 0.06 for player B. There is almost no transition from state L to state S (Figure 5(d)). Specifically, we can observe that player A is the type of player who advances the match by using drop shots after long balls, and player B is the type of player who advances the match by dividing into left and while pressing in with long balls.
As observed above, the players are not only anticipating the courses of the struck balls by using the kinematic clues as clues, but are also increasing the accuracy of the anticipation by relying on various contextual information, such as the position when the ball is struck and the status of the game. In this study, in addition to the position where the ball is struck, which has been cited as contextual information in previous studies, the state transition probability, which expresses the connection between two strokes, was also addressed. Owing to the method proposed herein, characteristic differences were observed in the struck ball sequence pattern of the players. Specifically, the struck ball course is not determined in accordance with the probability information, and corrections are added during the match based on other contextual information, such as the status of the game. However, this prior information is an important factor in in-


Figure 5. State transition matrix of each player and the Shannon diagram. Panel (a) and panel (b) show the W state. Panel (c) and pane (d) show the D state. Red and blue letters indicate the distinctive differences of the two players.
creasing a player’s predictive accuracy during competition.
4. Conclusion
This study proposed a method to apply the Markov model to the course of a ball struck by a player and measure the state transition probability to extract the characteristics of an effective struck ball course as a clue for anticipation. In this case, the state transition probability of a ball struck by a player was measured with the actual coordinate data of a soft tennis singles match. The characteristics observed show the struck ball sequence pattern for the player, which is an effective information for increasing the predictive accuracy of the course of a struck ball. If this information is provided to a player prior to a match, the player can almost certainly employ it to his/her advantage.
Moreover, in this study, the proposed method was explained using the actual data of a competition that was undertaken with the focus on the Asian region, namely soft tennis. However, this information may be fully applicable to major competitions, such as hard tennis and table tennis. In the future, it will probably be necessary to apply it to other net-type competitions and to verify further its effectiveness as an anticipation clue.
As this study involved an analysis of only two players, it will be possible to ascertain the effectiveness of the proposed method by analyzing the games of multiple players from this time forward.
Cite this paper
Kudo, T., Yamamoto, Y., Shinohara, H., & Kudo, R. (2017). State Transition Probability as the Anticipation Clue of the Course of a Struck Ball. Advances in Physical Education, 7, 343-353. https://doi.org/10.4236/ape.2017.73028
References
- 1. Abdel-Aziz, Y. I., & Karara, H. M. (2015). Direct Linear Transformation from Comparator Coordinates into Object Space Coordinates in Close-Range Photogrammetry. Photogrammetric Engineering & Remote Sensing, 81, 103-107.
https://doi.org/10.14358/PERS.81.2.103 [Paper reference 1] - 2. Abernethy, B. (1990). Anticipation in Squash: Differences in Advance Cue Utilization between Expert and Novice Players. Journal of Sports Sciences, 8, 17-34.
https://doi.org/10.1080/02640419008732128 [Paper reference 2] - 3. Abernethy, B., & Russell, D. G. (1987). The Relationship between Expertise and Visual Search Strategy in a Racquet Sport. Human Movement Science, 6, 283-319.
https://doi.org/10.1016/0167-9457(87)90001-7 [Paper reference 1] - 4. Bourne, M., Bennett, S. J., Hayes, S. J., & Williams, A. M. (2011). The Dynamical Structure of Handball Penalty Shots as a Function of Target Location. Human Movement Science, 30, 40-55.
https://doi.org/10.1016/j.humov.2010.11.001 [Paper reference 1] - 5. Gray, R. (2002). “Markov at the Bat”: A Model of Cognitive Processing in Baseball Batters. Psychological Science: A Journal of the American Psychological Society/APS, 13, 542-547.
https://doi.org/10.1111/1467-9280.00495 [Paper reference 1] - 6. Huys, R., Canal-Bruland, R., Hagemann, N., Beek, P. J., Smeeton, N. J., & Williams, A. M. (2009). Global Information Pickup Underpins Anticipation of Tennis Shot Direction. Journal of Motor Behavior, 41, 158-171.
https://doi.org/10.3200/JMBR.41.2.158-171 [Paper reference 1] - 7. Jackson, R. C., Warren, S., & Abernethy, B. (2006). Anticipation Skill and Susceptibility to Deceptive Movement. Acta Psychologica, 123, 355-371.
https://doi.org/10.1016/j.actpsy.2006.02.002 [Paper reference 1] - 8. Loffing, F., & Hagemann, N. (2014). On-Court Position Influences Skilled Tennis Players’ Anticipation of Shot Outcome. Journal of Sport & Exercise Psychology, 36, 14-26.
https://doi.org/10.1123/jsep.2013-0082 [Paper reference 1] - 9. McGarry, T., & Franks, I. M. (1994). A Stochastic Approach to Predicting Competition Squash Match-Play. Journal of Sports Sciences, 12, 573-584.
https://doi.org/10.1080/02640419408732208 [Paper reference 1] - 10. McGarry, T., & Franks, I. M. (1996). In Search of Invariant Athletic Behaviour in Sport: An Example from Championship Squash Match-Play. Journal of Sports Sciences, 14, 445-456.
https://doi.org/10.1080/02640419608727730 [Paper reference 1] - 11. Pfeiffer, M., Zhang, H., & Hohmann, A. (2010). A Markov Chain Model of Elite Table Tennis Competition. International Journal of Sports, 5, 205-222.
http://spo.sagepub.com/content/5/2/205.short [Paper reference 2] - 12. Savelsbergh, G. J. P., Williams, A. M., Van Der Kamp, J., & Ward, P. (2002). Visual Search, Anticipation and Expertise in Soccer Goalkeepers. Journal of Sports Sciences, 20, 279-287.
https://doi.org/10.1080/026404102317284826 [Paper reference 1] - 13. Smeeton, N. J., & Huys, R. (2011). Anticipation of Tennis-Shot Direction from Whole- Body Movement: The Role of Movement Amplitude and Dynamics. Human Movement Science, 30, 957-965.
https://doi.org/10.1016/j.humov.2010.07.012 [Paper reference 1] - 14. Williams, A. M., Huys, R., Canal-Bruland, R., & Hagemann, N. (2009). The Dynamical Information Underpinning Anticipation Skill. Human Movement Science, 28, 362-370.
https://doi.org/10.1016/j.humov.2008.10.006 [Paper reference 1] - 15. Williams, A. M., Ward, P., Knowles, J. M., & Smeeton, N. J. (2002). Anticipation Skill in a Real-World Task: Measurement, Training, and Transfer in Tennis. Journal of Experimental Psychology, 8, 259-270.
https://doi.org/10.1037/1076-898X.8.4.259 [Paper reference 2] - 16. Williams,. A M., Ward, P., Smeeton, N. J., & Allen, D. (2004). Developing Anticipation Skills in Tennis Using On-Court Instruction: Perception versus Perception and Action. Journal of Applied Sport Psychology, 16, 350-360.
https://doi.org/10.1080/10413200490518002 [Paper reference 1] - 17. Wong, R., & Zigarovich, M. (2007). Tennis with Markov. The College Mathematics Journal, 38, 53-55.
http://www.ingentaconnect.com/content/maa/cmj/2007/00000038/00000001/art00008 [Paper reference 1]








