Theoretical Economics Letters
Vol.06 No.06(2016), Article ID:73162,22 pages
10.4236/tel.2016.66124
Competition of Intermediaries in a Differentiated Duopoly
Sonja Brangewitz, Jochen Manegold
Department of Economics, Paderborn University, Paderborn, Germany
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 6, 2016; Accepted: December 26, 2016; Published: December 29, 2016
ABSTRACT
On an intermediate goods market with asymmetric production technologies as well as vertical and horizontal product differentiation, we analyze the influence of simultaneous competition for resources and customers. The intermediaries face either price or quantity competition on the output market and a monopolistic, strategically acting supplier on the input market. We find that there exist quality and productivity differences such that for quantity competition only one intermediary is willing to procure inputs from the input supplier, while for price competition both intermediaries are willing to purchase inputs. Moreover, the well-known welfare advantage of price competition can in general be no longer confirmed in our model with an endogenous input market and asymmetric intermediaries.
Keywords:
Input Market, Product Quality, Quantity Competition, Price Competition

1. Introduction
We consider a differentiated intermediate goods market in which two intermediaries compete for customers on the sales side as well as for inputs on the procurement side. Hereby, competition is on the sales side, either carried out by strategically choosing production quantities or by setting sales prices. In our context, differentiation on the one hand refers to horizontal product differentiation, i.e., products offered at the market can either be substitutes or complements. On the other hand we allow for quality differences between the intermediaries’ products and therefore products may also be vertically differentiated. In addition, asymmetries can also arise from efficiency differences of the intermediaries’ production technologies. A simple example of such a differentiated intermediate goods market that we have in mind is companies who produce furniture. They need to procure identical resources such as wood in order to produce chairs or tables and, therefore, face competition on the input market. In addition, they sell their products on a competitive output market, on which they compete for customers. Hereby, the companies may be differentiated horizontally and either offer substitute products, i.e., both producing tables, or both producing chairs, or complementary products, with one company offering chairs and the other one tables. We investigate the impact of simultaneous competition for resources and customer demand on the market equilibrium and highlight the influence of the market power of a monopolistic input supplier.
In the literature, two fundamental contributions in oligopoly theory are made by Cournot and Bertrand, in which firms produce a homogenous good and select quantities in the former and prices in the latter model. In the years after, these settings were extended in various directions. Referring to [1] , in their seminal work, [2] considers a differentiated duopoly allowing for complements and substitutes and compares the equilibrium outcomes of Bertrand and Cournot competition. [3] generalizes their model such that no special form of demand structure needs to be assumed. The approach of duopolies was later extended by allowing for 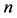 product varieties as for example by [4] [5] [6] and [7] . Moreover, not just horizontal (substitutes vs. complements) but also vertical product differentiation (product quality) finds attention within the literature. Most closely related to our setting is [8] who also has exogenously given asymmetric costs and asymmetric product qualities. In a slightly other direction goes the analysis [9] which focuses on the number of active firms, i.e., firms producing a positive quantity in Bertrand and Cournot equilibrium and considers homogeneous and differentiated products. One issue that is neglected in the above-mentioned contributions but plays a major role in our article is the market power of an input supplier and is addressed by [10] - [15] , among others. Related to our model but with a different objective, [10] considers a differentiated market with intermediaries and input suppliers and analyzes the impact of vertical mergers with an emphasis on social welfare. [12] focuses on a vertically differentiated duopoly, using a simplified version of the linear model by [1] and [2] . The fundamental difference to their approach is the incorporation of the market’s supply side and the resulting endogenous costs of production. A vertical market structure that is similar to the one discussed in our work and incorporates the market’s supply side is for example considered by [13] . They analyze an intermediate goods market in which a profit-maximizing input supplier interacts with two unequally productive intermediaries who provide a homogeneous final good. The price-setting input supplier has the possibility of either discriminating intermediaries in prices or choosing a uniform price. In their contribution, [13] emphasizes the importance of the intermediaries’ technology differences as well as the input supplier’s pricing strategy when comparing profits under Bertrand and Cournot competition. They show on the one hand that under Bertrand competition the input supplier’s profit, the aggregated profit of the input supplier and the intermediaries and social welfare are always higher than under Cournot competition, regardless of the pricing strategy. On the other hand a comparison of the intermediary’s profits across competition types can only be done conditional on technology differences between the intermediaries as well as the pricing strategy of the input supplier. Given that intermediaries are asymmetric in terms of productivity and the supplier charges uniform prices, their profit may be higher under price competition. Thus, the result of [2] in terms of profits does not necessarily hold in a vertically structured setting. Moreover, it is shown that the results of [11] and [12] cannot be confirmed if the input supplier charges a uniform price and intermediaries differ in productivity. Differently, a focus on the input supplier’s optimal price choice is put in the contribution of [15] . Related to our model, he considers a setting with an upstream market including a monopolistic supplier who provides an intermediate input good and an imperfectly competitive downstream market with intermediaries (retailers) producing differentiated products. The article analyzes the supplier’s optimal price choice depending on the downstream market structure, i.e., whether market entry is free or restricted. The optimal input price is depending on the number of downstream firms in case of free market entry.
product varieties as for example by [4] [5] [6] and [7] . Moreover, not just horizontal (substitutes vs. complements) but also vertical product differentiation (product quality) finds attention within the literature. Most closely related to our setting is [8] who also has exogenously given asymmetric costs and asymmetric product qualities. In a slightly other direction goes the analysis [9] which focuses on the number of active firms, i.e., firms producing a positive quantity in Bertrand and Cournot equilibrium and considers homogeneous and differentiated products. One issue that is neglected in the above-mentioned contributions but plays a major role in our article is the market power of an input supplier and is addressed by [10] - [15] , among others. Related to our model but with a different objective, [10] considers a differentiated market with intermediaries and input suppliers and analyzes the impact of vertical mergers with an emphasis on social welfare. [12] focuses on a vertically differentiated duopoly, using a simplified version of the linear model by [1] and [2] . The fundamental difference to their approach is the incorporation of the market’s supply side and the resulting endogenous costs of production. A vertical market structure that is similar to the one discussed in our work and incorporates the market’s supply side is for example considered by [13] . They analyze an intermediate goods market in which a profit-maximizing input supplier interacts with two unequally productive intermediaries who provide a homogeneous final good. The price-setting input supplier has the possibility of either discriminating intermediaries in prices or choosing a uniform price. In their contribution, [13] emphasizes the importance of the intermediaries’ technology differences as well as the input supplier’s pricing strategy when comparing profits under Bertrand and Cournot competition. They show on the one hand that under Bertrand competition the input supplier’s profit, the aggregated profit of the input supplier and the intermediaries and social welfare are always higher than under Cournot competition, regardless of the pricing strategy. On the other hand a comparison of the intermediary’s profits across competition types can only be done conditional on technology differences between the intermediaries as well as the pricing strategy of the input supplier. Given that intermediaries are asymmetric in terms of productivity and the supplier charges uniform prices, their profit may be higher under price competition. Thus, the result of [2] in terms of profits does not necessarily hold in a vertically structured setting. Moreover, it is shown that the results of [11] and [12] cannot be confirmed if the input supplier charges a uniform price and intermediaries differ in productivity. Differently, a focus on the input supplier’s optimal price choice is put in the contribution of [15] . Related to our model, he considers a setting with an upstream market including a monopolistic supplier who provides an intermediate input good and an imperfectly competitive downstream market with intermediaries (retailers) producing differentiated products. The article analyzes the supplier’s optimal price choice depending on the downstream market structure, i.e., whether market entry is free or restricted. The optimal input price is depending on the number of downstream firms in case of free market entry.
While considering vertical and horizontal product differentiation, the focus of our analysis is put on the impact of simultaneous competition for resources and customer demand on the market outcome under Cournot and Bertrand competition with two intermediaries. The input prices are determined first and intermediaries compete by choosing quantities or prices afterwards. For the competition stage, we analyze the effect of the intermediaries’ asymmetries on the market outcome. In this context we find that there exist quality and productivity differences such that for quantity competition only one intermediary is willing to procure inputs from the input supplier, while for price competition both intermediaries are willing to purchase inputs.
The formal analysis in the forthcoming sections is backwards and proceeds as follows: Section 2 presents the basic model. We begin with the assumptions on the customer’s demand, followed by the analysis of two different modes of competition between the intermediaries. As proposed in [10] we explicitly consider an input market with a monopolistic input supplier. We start with quantity competition, investigate price competition and compare them afterwards in Section 3. A final conclusion is made in Section 4, whereas additional computations and proofs can be found in Appendix.
2. The Model
In order to allow for substitutable as well as for complementary products of the intermediaries, we assume that a representative customer has a utility function, which is of the following standard form as for instance in [2] :
 (1)
(1)
Hereby, 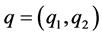 denotes the quantities the customer buys from each of the two intermediaries. The parameter
denotes the quantities the customer buys from each of the two intermediaries. The parameter 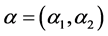 indicates the customer’s valuation for the quality of the according product. For simplicity reasons we will denote
indicates the customer’s valuation for the quality of the according product. For simplicity reasons we will denote 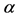 as product quality in the following. The variable
as product quality in the following. The variable 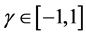 represents the degree of horizontal product differentiation and defines whether products of the intermediaries are substitutable, complementary or independent. If
represents the degree of horizontal product differentiation and defines whether products of the intermediaries are substitutable, complementary or independent. If  the products are perfect complements, if
the products are perfect complements, if 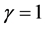 they are perfect substitutes, while
they are perfect substitutes, while  describes the case where products are independent and thus, both intermediaries are monopolists. We assume the customer to maximize his utility subject to the budget constraint
describes the case where products are independent and thus, both intermediaries are monopolists. We assume the customer to maximize his utility subject to the budget constraint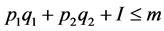 , where
, where  is the customer’s income and
is the customer’s income and 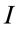 his consumption of other goods. The customer’s income is assumed to be sufficiently large such that utility maximization leads to an inner solution. Taking prices
his consumption of other goods. The customer’s income is assumed to be sufficiently large such that utility maximization leads to an inner solution. Taking prices 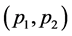 as given, the customer optimally chooses to buy and consume those quantities
as given, the customer optimally chooses to buy and consume those quantities 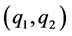 that maximize his utility function subject to his budget constraint, satisfying
that maximize his utility function subject to his budget constraint, satisfying
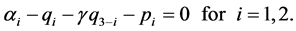 (2)
(2)
As in [13] , the two intermediaries may differ in their productivity to transform inputs to a final product, i.e., intermediary  needs
needs 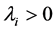 input units to produce one unit of his final product
input units to produce one unit of his final product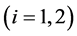 . Therefore, asymmetries between intermediaries may arise from distinct product qualities and from differences in input productivities. To
. Therefore, asymmetries between intermediaries may arise from distinct product qualities and from differences in input productivities. To
describe these asymmetries we refer to 

Within Cournot competition the two intermediaries compete by strategically choosing the quantities they produce. The price that intermediary 


where 




where 



Within Bertrand competition the two intermediaries compete by strategically choosing the prices of their products. The according quantities intermediaries are producing depend on the prices that both charge at the market. Given both intermediaries compete, by using Equation (2) and assuming 

Thus, intermediary

By using Equation (7) we compute intermediary

Given the intermediaries best reply functions for Cournot and Bertrand competition we compute the equilibrium quantities and prices for both modes of competition in Appendix 1.1. We make the following restriction on the asymmetries that we consider in our analysis.
Assumption 1. We assume 

With this assumption we exclude the range of parameters for which asymmetries drive the inefficient intermediary immediately out of the market in at least one mode of competition. However as long as the intermediaries’ products are complementary, these assumptions are always satisfied and, thus, this effectively restricts our analysis only for substitutable products.
Taking the intermediaries’ equilibrium quantities and prices as given, we next determine the optimal input price the monopolistic input supplier chooses. The total market demand on the input market is 


Lemma 1. Suppose the intermediaries compete either in choosing quantities or prices and Assumption 1 holds. If the two intermediaries are sufficiently asymmetric and there exists an inner solution for the monopolistic input price, then it is optimal for the input supplier to choose an input price such that he sells his inputs to just one intermediary and thus excludes the other intermediary from the input market.
As the proof Lemma 1 shows the asymmetries required for the statement in Lemma 1 are actually depending on the mode of competition, denoted by



contrast, if the intermediaries are sufficiently symmetric, which is 

3. Comparison of the Two Modes of Competition
For this section we assume 
Proposition 1. Suppose Assumption 1 holds. There exist parameters 


Proposition 1 makes clear that there exist quality and productivity differences such that in Cournot competition only one intermediary is willing to procure inputs from the input supplier while in Bertrand competition still both intermediaries are willing to purchase inputs. This is illustrated in Figure 1.
Hence, in Proposition 1 we establish that there is no situation in which Bertrand competition leads to an exclusion of one intermediary from the input market while Cournot competition does not. The reason is that the profits of the input supplier, given he sells to both intermediaries, are always higher when intermediaries compete in Bertrand compared to Cournot competition. Therefore, if the asymmetries between the two intermediaries increase, the input price of a profit-maximizing input supplier is raised earlier under Cournot competition than under Bertrand competition. This has the consequence that under Cournot competition the input price is earlier too high for the intermediary with quality and/or productivity disadvantages. Thus, he is no longer
Figure 1. The input market for
willing to purchase inputs. Thus, the observation of Proposition 1 divides the range of asymmetries into different regions of large, intermediate and small asymmetries between the two intermediaries. The next proposition explicitly compares the input prices for the three scenarios from Proposition 1 and Figure 1.
Proposition 2 (Input Prices). Suppose Assumption 1 holds.
1. For large asymmetries between the intermediaries the input prices are equal under Cournot and Bertrand competition.
2. For intermediate asymmetries between the intermediaries the input prices are always higher under Cournot than under Bertrand competition.
3. Consider small asymmetries between the intermediaries. If input productivities are identical, both intermediaries act as monopolists or both intermediaries produce identical relative qualities, then under Cournot and Bertrand competition the input prices are equal. If the goods are substitutes and the relative quality of the less productive intermediary is higher, then input prices are higher under Bertrand than under Cournot competition. If the goods are complements and the relative quality of the less productive intermediary is higher, then input prices are higher under Cournot than under Bertrand competition.
Proposition 2 indeed confirms the intuition behind Proposition 1. The first statement for large asymmetries is obvious. As for Bertrand and Cournot competition the input supplier sets an input price that excludes one intermediary from the market and sells just to the other intermediary, there is no longer competition on the output market between the intermediaries. Thus, there is no difference in input prices. The second statement for intermediate asymmetries confirms that the input price under Cournot competition is indeed too high for one intermediary to purchase positive quantities on the input market, while the input price is always lower under Bertrand competition. However, for the last constellation of parameters with small asymmetries the comparison of the input prices for Cournot and Bertrand competition depends on several parameters. In the proof of Proposition 2 we establish that for small asymmetries, i.e.,



In order to analyze the intermediaries’ incentives to invest in product quality, the next two Propositions now compare the intermediaries’ equilibrium prices, quantities and profits for Cournot and Bertrand competition.
Proposition 3. Suppose both intermediaries have equal productivities and product qualities and
However, this observation does not carry over to arbitrary degrees of asymmetry as the next proposition establishes.
Proposition 4. Suppose Assumption 1 holds.
1. There exist asymmetries such that there is an intermediary who sets strictly lower prices in Cournot competition than in Bertrand competition.
2. There exist asymmetries such that there is an intermediary who produces a strictly greater quantity in Cournot competition than in Bertrand competition.
3. There exist asymmetries for substitutable products such that the profits for both intermediaries are strictly lower in Cournot competition than in Bertrand competition.
For our model with symmetric intermediaries, Proposition 3 confirms a prominent result from the literature. [2] shows for a linear demand structure that in equilibrium Bertrand competition is more efficient than Cournot competition, as it generates a lower price and a higher output level. They find that this result is independent of whether goods are substitutes or complements and regardless of the demand structure’s degree of symmetry. Thus, Bertrand competition implies a higher consumer and total welfare. Furthermore, [2] shows that firms prefer to select quantities (prices), if goods are substitutes (complements). However, Proposition 4 establishes that this must not always be true when the input market is explicitly modeled and asymmetries between the intermediaries are present. [8] , in a setting with quality and cost asymmetries, finds the same relations in terms of equilibrium prices and quantities as in Proposition 3. Nevertheless, in our model with an endogenous input market this relationship cannot always be guaranteed.
4. Conclusion
We analyzed the influence of asymmetries between intermediaries on an intermediate goods market with horizontal and vertical product differentiation. We established that introducing a strategically acting input supplier may lead to exclusion of one intermediary from the input market if the asymmetries are sufficiently large (Lemma 1). There exists a range of asymmetries where in Cournot competition the input prices are too high for one intermediary, while in Bertrand competition both intermediaries demand positive quantities on the input market (Propositions 1 and 2). Including a strategically acting input supplier into the model tends to make the competition framework more realistic. It highlights the differences between price and quantity competition depending on the degree of product differentiation. As a managerial implication, firms should also pay attention to the degrees of asymmetries in the market since a strategic input supplier adjusts his price accordingly. From a theoretical point of view and in comparison to [8] , we excluded the range of parameters for which asymmetries drove the inefficient firm immediately out of the market ( [8] , Equation (8)). However, due to the explicit inclusion of the input market, we make no initial assumption on the relation between qualities and input prices as done in [8] . Nevertheless, in our model with a strategically acting input supplier and thus, an endogenously determined input price, this exclusion from the input market even survives for a more restrictive range of asymmetries. Our bound on the asymmetries is established for substitutable as well as for complementary products with
Acknowledgements
We are grateful to Claus-Jochen Haake for constructive suggestions and comments. This work was partially supported by the German Research Foundation (DFG) within the Collaborative Research Centre “On-The-Fly Computing” (SFB 901). An earlier version can be found as Working Paper No. 2015-04, CIE Center for International Economics Working Papers, Paderborn University. An extended version of this article is going to be part of the dissertation of Jochen Manegold.
Cite this paper
Brangewitz, S. and Manegold, J. (2016) Competition of Intermediaries in a Differentiated Duopoly. Theoreti- cal Economics Letters, 6, 1341-1362. http://dx.doi.org/10.4236/tel.2016.66124
References
- 1. Dixit, A. (1979) A Model of Duopoly Suggesting a Theory of Entry Barriers. The Bell Journal of Economics, 10, 20-32.
https://doi.org/10.2307/3003317 - 2. Singh, N. and Vives, X. (1984) Price and Quantity Competition in a Differentiated Duopoly. The RAND Journal of Economics, 15, 546-554.
- 3. Cheng, L. (1985) Comparing Bertrand and Cournot Equilibria: A Geometric Approach. The RAND Journal of Economics, 16, 146-152.
- 4. Vives, X. (1985) On the Efficiency of Bertrand and Cournot Equilibria with Product Differentation. Journal of Economic Theory, 36, 166-175.
https://doi.org/10.1016/0022-0531(85)90086-9 - 5. Okuguchi, K. (1987) Equilibrium Prices in the Bertrand and Cournot Oligopolies. Journal of Economic Theory, 42, 128-139.
https://doi.org/10.1016/0022-0531(87)90106-2 - 6. Hackner, J. (2000) A Note on Price and Quantity Competition in Differentiated Oligopolies. Journal of Economic Theory, 93, 233-239.
https://doi.org/10.1006/jeth.2000.2654 - 7. Amir, R. and Jin, J.Y. (2001) Cournot and Bertrand Equilibria Compared: Substitutability, Complementarity and Concavity. International Journal of Industrial Organization, 19, 303-317.
https://doi.org/10.1016/S0167-7187(99)00043-0 - 8. Zanchettin, P. (2006) Differentiated Duopoly with Asymmetric Costs. Journal of Economics & Management Strategy, 15, 999-1015.
https://doi.org/10.1111/j.1530-9134.2006.00125.x - 9. Ledvina, A.F. and Sircar, R. (2011) Bertrand and Cournot Competition under Asymmetric Costs: Number of Active Firms in Equilibrium. Available at SSRN 1692957.
https://doi.org/10.2139/ssrn.1692957 - 10. Hackner, J. (2003) Vertical Integration and Competition Policy. Journal of Regulatory Economics, 24, 213-222.
https://doi.org/10.1023/A:1024790112185 - 11. Correa-López, M. and Naylor, R.A. (2004) The Cournot-Bertrand Profit Differential: A Reversal Result in a Differentiated Duopoly with Wage Bargaining. European Economic Review, 48, 681-696.
https://doi.org/10.1016/S0014-2921(02)00326-4 - 12. Correa-López, M. (2007) Price and Quantity Competition in a Differentiated Duopoly with Upstream Suppliers. Journal of Economics & Management Strategy, 16, 469-505.
https://doi.org/10.1111/j.1530-9134.2007.00146.x - 13. Mukherjee, A., Broll, U. and Mukherjee, S. (2012) Bertrand versus Cournot Competition in a Vertical Structure: A Note. The Manchester School, 80, 545-559.
https://doi.org/10.1111/j.1467-9957.2012.02228.x - 14. Manasakis, C. and Vlassis, M. (2014) Downstream Mode of Competition with Upstream Market Power. Research in Economics, 68, 84-93.
https://doi.org/10.1016/j.rie.2013.12.002 - 15. Pinopoulos, I.N. (2011) Input Pricing by an Upstream Monopolist into Imperfectly Competitive Downstream Markets. Research in Economics, 65, 144-151.
https://doi.org/10.1016/j.rie.2010.05.004
Appendix
1.1. Computations
Equilibrium Prices and Quantities
We start with Cournot Competition. By using the best reply functions of both intermediaries we compute intermediary

The according equilibrium price 

In order to guarantee the quantity to be non-decreasing in ‘‘weighted’’ qualities given by 

Assumption 2. We assume 

We restrict our analysis to parameter choices 
For Bertrand competition the Nash equilibrium price is given by
and the equilibrium quantity is given by
For similar reasons as in Cournot competition we impose an analogue assumption on the parameter choices 
Assumption 1.We assume 

We restrict our analysis to parameter choices 
Total Demand on the Input Market
Taking the intermediaries’ equilibrium quantities and prices as given, we determine the total market demand on the input market given by
and
The Intermediaries’ Profits
We now summarize their profits using Lemma 1. The profits for the scenarios identified in Proposition 1 and Figure 1 can easily be derived accordingly. Consider
and
1.2. Proofs
Proof of Lemma 1
Proof of Lemma 1. For both modes of competition the proof proceeds in two steps. In a first step we determine the prices the input supplier charges. In doing so we distinguish different cases depending on the number of intermediaries demanding positive quantities. Afterwards the according profits are compared in step two.
We start with Cournot Competition.
Step 1 (Input Prices and Profits)
Case 1:The input price is chosen such that both intermediaries produce strictly positive quantities. Therefore, the following must hold:
Maximizing the profit of the input supplier 
Note that for this input price both intermediaries indeed purchase positive quantities. Suppose



and thus,
By using
this implies that
Rearranging yields
showing that the input price 
Case 2: The input price is chosen such that intermediary 1 produces a strictly positive quantity while intermediary 2 produces zero. Thus, we require
which implies

Note that by definition this input price is indeed too high for intermediary 2 to purchase positive quantities. The analogous argument holds if intermediary 2 produces a strictly positive quantity while intermediary 1 produces zero. The profit of the input supplier is
Case 3: The input price is too high for at least one intermediary to purchase strictly positive quantities.
Step 2 (Comparing Profits)
An input price as suggested in Case 3 cannot be optimal. In this scenario the input price is too high for the intermediaries to demand goods and the input supplier’s profit is zero. In contrast, Case 1 as well as Case 2 yields positive profits. Therefore, we analyze the input supplier’s profits for Cases 1 and 2. We compare the two monopoly profits for selling to intermediary 1 with the duopoly profits for selling to both intermediaries.
Thus, suppose
Step 2.1: We compare the two monopoly profits for selling to intermediary 1 and obtain by observing
that
Step 2.2: We compare the duopoly profit with the monopoly profit for selling to intermediary 1. If the duopoly profit is greater than or equal to both monopoly profits, then the input supplier decides to sell to both intermediaries. Therefore, we obtain that if
with
then
holds. Thus, whenever 
the input supplier prefers to set a price for which both intermediaries procure inputs. Note that the following is always true:
Step 2.1 and Step 2.2 show that for 


In summary, if for Cournot competition 
with
then it is optimal for a profit-maximizing input supplier to only serve intermediary 1 and with analogous conditions to serve intermediary 2.
We now turn to the analysis of Bertrand Competition.
Step 1 (Input Prices and Profits)
Case 1: The input price is chosen such that both intermediaries produce strictly positive quantities. Therefore, the following must hold:
Maximizing the profit of the input supplier 
Note that for this input price both intermediaries indeed purchase positive quantities. Suppose



and thus,
which implies when using
that
Rearranging yields
showing that the input price 
Case 2: The input price is chosen such that intermediary 1 produces a strictly positive quantity while intermediary 2 produces zero. Thus, we require
which implies
Note that by definition this input price is indeed too high for intermediary 2 to purchase positive quantities. The analogous argument holds if intermediary 2 produces a strictly positive quantity while intermediary 1 produces zero. The profit of the input supplier is
Case 3: The input price is too high for at least one intermediary to purchase strictly positive quantities.
Step 2 (Comparing Profits)
As in Cournot competition, it suffices to compare the profits of the input supplier for Cases 1 and 2. We compare the two monopoly profits for selling to intermediary 1 with the duopoly profits for selling to both intermediaries. Thus, suppose
Step 2.1: We compare the two monopoly profits for selling to intermediary 1. We obtain by observing
that
Step 2.2: We compare the duopoly profit with the monopoly profit for selling to intermediary 1. If the duopoly profit is greater than or equal to both monopoly profits, then the input supplier decides to sell to both intermediaries. Therefore, we obtain that if
with
then
holds. Thus, whenever 
the input supplier prefers to set a price to sell to both intermediaries. Note that the following is always true:
Step 2.1 and Step 2.2 show that for 


In summary, if for Bertrand competition 
with
then it is optimal for a profit-maximizing input supplier to only serve intermediary 1 and with analogous conditions to serve intermediary 2.
Proof of Proposition 1
Proof of Proposition 1. The proof proceeds in two steps. First we compare the profits of the input supplier in the case of intermediaries competing in quantities with the setting in which intermediaries compete in prices.
Step 1 (Duopoly Profit of the Input Supplier)
Suppose the input supplier sells inputs to both intermediaries, which is
We show that 
can be rewritten as
Assumption 1 and 2 (from Appendix 1.1), which is
implies for 
Thus, we obtain
The analogous argument holds for

and with Assumption 1 (from Appendix 1.1) for
Step 2 (Comparing 

Note that 

With the observation that the input supplier’s profit when selling to both intermediaries is non-decreasing in 





Proof of Proposition 2
Case 1: Large asymmetries between the intermediaries, i.e., 
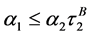
In Bertrand as well as in Cournot competition intermediary 2 is excluded from the input market. As the input demand of the intermediary is identical for both modes of competition, the input price is identical also.
Case 2: Intermediate asymmetries between the intermediaries, i.e., 

In Bertrand competition both intermediaries purchase inputs, while in Cournot competition only intermediary 1 procures on the input market. We have
Therefore, 


Case 3: Small asymmetries between the intermediaries, i.e., 

Both intermediaries purchase inputs on the input market in Bertrand as well as in Cournot competition. We have
Therefore, 

Proof of Proposition 3
Proof of Proposition 3. For 

Thus, 


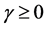



Proof of Proposition 4
Proof of Proposition 4. For this proof consider small asymmetries between the intermediaries, i.e., 


1. We have



2. We have



3. We have










































































