Received 21 March 2016; accepted 3 June 2016; published 6 June 2016

ABSTRACT

Starting from an intuitive and constructive approach for countable domains, and combining this with elementary measure theory, we obtain an upper semi-continuous utility function based on outer measure. Whenever preferences over an arbitrary domain can at all be represented by a utility function, our function does the job. Moreover, whenever the preference domain is endowed with a topology that makes the preferences upper semi-continuous, so is our utility function. Although links between utility theory and measure theory have been pointed out before, to the best of our knowledge, this is the first time that the present intuitive and straight-forward route has been taken.

Keywords:

Preferences, Utility Theory, Measure Theory, Outer Measure

1. Introduction

When treating utility theory, traditional economic textbooks discuss two disparate cases in considerable detail: the potential non-existence of utility functions for complete and transitive preference relations on non-trivial connected Euclidean domains―usually illustrated by lexicographic preferences (Debreu, [1] )―and the existence of continuous utility functions for complete, transitive and continuous preferences on connected Euclidean domains; see, e.g. Mas-Colell, Whinston, and Green [2] . Yet, for many purposes, in particular for the existence of a best alternative in a compact set of alternatives, a weaker property―upper semi-continuity―suffices. Hence, the reader of such a textbook treatment might wonder if there exist upper semi-continuous utility functions, and whether this is true even if the domain is not connected.

The purpose of this note is primarily pedagogical: it provides necessary and sufficient conditions for the existence of upper semi-continuous utility functions on arbitrary domains; see Theorem 2 and the text following it. Our approach is intuitive, constructive, and although it uses a measure-theoretic idea, it remains easily accessible to readers without any knowledge of measure theory.

Measure theory is the branch of mathematics that deals with the question of how to define the “size” (area/ volume) of sets. The main pedagogical point of our paper is to formalize a direct, intuitive link with utility theory: given a binary preference relation on a set of alternatives, the “better” an alternative is, the “larger” is its set of worse alternatives. So if one can measure the “size” of the set of worse elements, for each given alternative, one obtains a utility function.

To be a bit more precise, measure theory starts out by first defining the “size”―measure―of a class of “simple” sets, such as bounded intervals on the real line or rectangles in the plane, and then extends this definition to other sets by way of approximation in terms of simple sets. The outer measure is the best such approximation “from above”. This is illustrated in Figure 1: having defined the size of rectangles in the plane, we can assign a size also to more general sets S in the plane by covering it with rectangles. That can be done in many ways, but to get a good approximation, one wants a covering that resembles S as closely as possible. Roughly speaking, the rectangles covering S should not stick out from S a lot. So the outer measure S is the infimum, over all coverings by a countable number of rectangles, of the sum of the rectangles’ areas. In more general settings, the outer measure is defined likewise as the infimum over coverings whose sizes have been defined (see, for instance, Rudin [3] , p. 304; Royden [4] , Sec. 3.2; Billingsley [5] , Sec. 3; Ash [6] , p. 14).

We follow this approach to define the utility of an alternative as the outer measure of its set of worse alternatives. We start by doing this for a countable set of alternatives, where this is relatively simple and then proceed to arbitrary sets.

Our paper is not the first to use tools from measure theory to address the question of utility representation: pioneering papers are Neuefeind [7] and Sondermann [8] . See Bridges and Mehta ( [9] , sections 2.2 and 4.3) for a textbook treatment. However, our approach differs fundamentally from these precursors. Firstly, we only use the basic notion of outer measure, while the mentioned studies impose additional topological and/or measure- theoretic constraints.¹ To the best of our knowledge, the logical connection between outer measure and utility has never been made before. We hope that this link between utility theory and measure theory is more explicit, intuitive and mathematically elementary than the above-mentioned approaches. Let us stress the generality of this result. Although the utility function in terms of outer measure is simple and intuitive, it delivers the most general results possible. Firstly, whenever preferences over an arbitrary set of alternatives can be represented by a utility function, our function does the job (cf. Theorem 1). Secondly, whenever the set of alternatives is endowed with a topology that makes preferences upper semi-continuous, also our utility function becomes upper semi-continuous (cf. Theorem 2).

The rest of the paper is organized as follows. Section 2 recalls definitions and provides notation. Section 3 contains the main results; one proof is in the Appendix.

2. Preliminaries

Let preferences on an arbitrary set X be defined in terms of a binary relation (“weakly preferred to”) which is:

complete: for all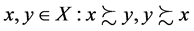, or both;

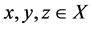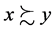transitive: for all: if and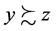, then.

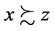As usual, means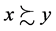, but not, whereas 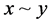means that both 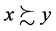and. The sets of elements strictly worse and strictly better than 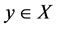are denoted

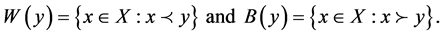
For with, the “open interval” of alternatives better than x but worse than y is denoted

A preference relation is represented by a function if

(1)

Any such function u is called a utility function for the preference relation in question.

3. Constructing the Utility Function

This section makes the intuitive argument from the introduction precise: given a binary preference relation on a set of alternatives, the “better” an alternative is, the “larger” is its set of worse alternatives. So if one can measure the “size” of the set of worse elements, for each given alternative, one obtains a utility function.

Although our construction borrows its main idea from measure theory, it ought to be stressed that no topological or measure-theoretic assumptions are needed: the way we define the utility function works whenever the necessary and sufficient conditions for the existence of a utility function are satisfied. The purpose of the more technical second subsection is to show a stronger result, namely that our utility function automatically inherits a commonly imposed continuity property of the preferences. Here, of course, some topology is required to define continuity.

3.1. Existence

A complete, transitive binary relation on a set X can be represented by a utility function if and only if it is Jaffray order separable² (Jaffray, [10] ): there is a countable set such that for all:

(2)

Roughly speaking, countably many alternatives suffice to keep all pairs with apart: x lies on one side of d and, whereas y lies on the other. To make our search for a (usc) utility representation at all meaningful, we will henceforth focus on preference relations that are Jaffray order separable.

Note that Jaffray order separability is satisfied automatically if the domain X itself is countable: you can simply take D equal to X. For uncountable domains, like commodity bundles in, it is often―for instance under suitable continuity assumptions―the case that the countable subset that does the trick is the set D of commodity bundles with rational coordinates.

The set D in the definition of Jaffray order separability is countable, so let be an injection. Finding a utility function on D is easy. Give each element d of D a positive weight such that weights have a finite sum and use the total weight of the elements weakly worse than d as the utility of d. For instance, give

weight to the alternative d with label, weight to the alternative d with label, and inductively, weight to the alternative d with label. In general, let be a summable sequence of positive weights; without loss of generality its sum is one. Assign to each weight.³ Define for each by. Clearly, (1) is satisfied.⁴

We can extend this procedure from D to X as follows. Let be the collection of subsets and define as follows:, and for:

(3)

Notice that is countable and that it is a covering of X. Extend to an outer measure on X in the usual way (recall Figure 1): for each set, define as the smallest total size of sets in covering A. Formally, a countable collection of sets from covers A if. Now define

where the infimum is taken over all countable collections that cover A.

Define for each as the outer measure of the set of elements worse than x:

(4)

It is easily seen that this gives the desired utility representation:

Theorem 1. Consider a complete, transitive, Jaffray order separable binary relation on an arbitrary set X. The function u in (4) is a utility function for.

Proof. By definition,

(5)

and the outer measure is monotonic: if, then.

We prove that u represents, i.e., we prove (1). Let. If, then by transitivity of, so. If, there are with by (2). By monotonicity of and (5):.

So finding a utility function is not so difficult; in fact, the literature we cite gives many other constructions as well. Our main message in this subsection is rather that our approach is from scratch, following an elementary idea of assigning an appropriate size to the set of worse elements. And it works without any topological or measure-theoretic assumptions on the domain: whenever preferences over an arbitrary set X can be represented by a utility function (i.e., they are complete, transitive, Jaffray order separable), our function does the job.

Perhaps a more important insight is that it automatically inherits a standard continuity property that is often imposed to guarantee the existence of most preferred elements; this part of the paper is a bit more technical and requires some further definitions.

3.2. Upper Semi-Continuity of the Outer-Measure Utility

By letting in a little bit of topology, one can use the above to obtain results concerning the existence of upper semi-continuous utility functions. Given a topology on X, preferences are:

continuous if for each, and are open;

upper semi-continuous (usc) if for each, is open.

Similarly, a function is usc if for each, is open.

Three important topologies are, firstly, the order topology, generated by (i.e., the smallest topology containing) the collections and; secondly, the lower order topology, generated by the collection, and thirdly, for any subset, the D-lower order topology, generated by the

collection. By definition, the order topology is the coarsest topology in which is continuous; the lower order topology is the coarsest topology in which is usc.

As mentioned in the introduction, although one often appeals to continuity to establish existence of most preferred alternatives, the weaker requirement of upper semi-continuity suffices: consider a complete, transitive, usc binary relation over a compact set X. If X has no most preferred element, then for each, there is a with, i.e., the collection is a covering of X with (by usc) open sets. By

compactness, there are finitely many such that cover X. Let be the most preferred element of. Then covers the entire set X, a contradiction.

From Theorem 1, we already know that our utility function defined in (4) represents preferences in all scenarios where utility functions exist. Our next result shows that whenever X is endowed with a topology that makes the preferences usc, also our utility function becomes usc.

Theorem 2. Consider a complete, transitive, Jaffray order separable binary relation on an arbitrary set X. The utility function u in (4) is usc in the D-lower order topology.

The proof is in the appendix. Corollaries 1 and 2 below provide applications of this result. Consider preferences over a topological space X with countable base.⁵ If is usc in this topology, it is Jaffray order separable (Rader, [12] ). By assumption, is open for each, so the topology on X is finer than the D-lower order topology. Hence, Theorem 2 applies:

Corollary 1. If is a complete, transitive, usc binary relation over a topological space X with countable base, the utility function in (4) represents and is usc.

Also Rader [12] establishes existence of a usc utility function under the conditions of Corollary 1. However, we obtain the result as a special case of Theorem 2, which holds under weaker conditions and gives a specific usc utility function building upon basic measure-theoretic intuition.

Sondermann [8] calls a preference relation on a set X perfectly separable if there is a countable set such that for all, with and for all, the following holds:

Perfect separability implies Jaffray order separability (Jaffray, [10] ), so we obtain the following result, due to Sondermann [8] , as a special case:

Corollary 2. (Sondermann, [8] , Corollary 2) Consider a complete, transitive, perfectly separable binary relation on a set X. Then there is a utility function representing, usc in any topology equal to or finer than the lower order topology.

Also here, the “value added” of Theorem 2 is that it provides a specific usc utility function building upon basic measure-theoretic intuition.

Acknowledgements

We are grateful to Avinash Dixit, Klaus Ritzberger, and Peter Wakker for comments and to the Knut and Alice Wallenberg Foundation and the Wallander-Hedelius Foundation for financial support.

Cite this paper

Mark Voorneveld,Jörgen W. Weibull, (2016) An Elementary Proof That Well-Behaved Utility Functions Exist. Theoretical Economics Letters,06,450-457. doi: 10.4236/tel.2016.63051

References

Appendix: Proof of Theorem 2

Recall that

and that the outer measure is monotonic: if, then.

To establish upper semi-continuity, let. We show that is open. To avoid trivialities, assume that equals neither nor X. Hence, there is a with. Let have. In particular,. It suffices to show that there is an open neighborhood V of x with for each.

Case 1: There is no with. As D may be assumed to contain a worst element of X, if such exists (see footnote 1),. By definition of, there are with and

. As, the set is nonempty. As

and, for each. So for each there is a with. We

show that for some. Suppose, to the contrary, that for each. For each, the set is infinite: otherwise, it has a best element, but then

is a proper subset of by Jaffray order separability, contradicting

. Let and let. By the above, there are infinitely many with

, contradicting that. We conclude that for some

. So, an open set in the D-lower order topology, and for each:.

Case 2: There is a with. Using (2) and:.

Case 2A: There is a with. Then is open in the D-lower order topology, contains x, and for each.

Case 2B: For each,. Then by (2), there is, for each, a that is strictly worse:. So is infinite. Since the sequence of weights

is summable, there is a such that. Since there are only finitely many

with, there is a such that for each with.

Since, , which is open in the D-lower order topology. Using and the construction of:

and

Hence, for each,

This concludes the proof. As a final remark, observe that due to the completeness of preferences, the countable collection of “simple” sets that we use to cover others is nested: for each pair of sets, either or. With minor changes, our proof can then be used to show that for each and each covering of, we can pick a single set that also covers. Therefore, the utility function in (4) can be rewritten as

Whenever x is not a most preferred alternative in X, Jaffray order separability assures that there is a with, so: the most precise covering of does not use the entire set X. So in that case we can simplify the expression further and write

Jaffray ( [10] , p. 982) defines utility similar to the expression in the previous line, but, so to speak, from the opposite direction: he defines utility of an alternative x as the supremum of the utility of worse ones from a suitably chosen countable set.

NOTES

¹Neuefeind [7] restricts attention to finite-dimensional Euclidean spaces and assumes that indifference sets have Lebesgue measure zero. Sondermann [8] assumes that preferences are defined on a probability space or a second countable topological space; see also Corollary 2 below.

²See Fishburn ( [11] , Section 3.1) or Bridges and Mehta ( [9] , Section 1.4) for alternative necessary and sufficient separability conditions.

³If there is a worst element in X (an with for all), one may assume without loss of generality that D contains one such element, say. Its weight can be normalized to zero:. This will assure that in (3).

⁴In class, we usually illustrate this common construction of utility functions on a countable domain D using chocolate bars: since D is countable, we may label its elements. Now break a chocolate bar in two pieces and place the first piece on. Then break the remaining piece in two and place one piece on. Then break the remaining piece in two and place one piece on, etc. Letting denote the weight of the chocolate placed on alternative, with, the aggregate weight of any subset is finite (at most one chocolate bar) and the utility function that we defined on the countable set D assigns to each alternative d the total weight of chocolate placed on pieces that are weakly worse than d.

⁵E.g., consumer preferences over a commodity space () with its standard Euclidean topology.