Received 24 February 2016; accepted 19 April 2016; published 22 April 2016

ABSTRACT

This paper describes how social capital emerges, relates to economic performance and evolves in the long run. Using the concept of psychological equilibrium, two types of individuals are generated in the population regarding their willingness to cooperate. We propose an evolutionary (learning) process over those types driven by the total payoffs of the psychological game, and provide a complete description of its dynamics. Macro-perceptions, defined as the individual perception of how cooperative the society is as a whole, are key to explain convergence to the full social capital state in the long run.

Keywords:

Psychological Equilibrium, Belief-Dependent Behavior, Evolutionary Games, Replicator Dynamics, Economic Development

1. Introduction

The aim of this paper is to explain how social capital is created, evolves and how it is related to economic performance and perceptions. Our main contributions are the following: Firstly, we introduce the concept of macro-perceptions as the individual and common perception of how likely cooperation is in a society. Social capital is framed through the likelihood of cooperation in a Prisoner’s Dilemma game. Secondly, a standard replicator dynamics is adopted in this context. We show that if there are enough people favorable to social capital and if macro-perceptions are optimistic enough, then society tends to be populated only by those favora- ble to social capital in the long run. Also, the best economic outcome is achieved in this case. Finally, the paper characterizes long-run performance under various conditions and carries out several comparative statics in terms of macro-perceptions, the size of the economy or the material payoff weight in the utility function.

The term social capital refers in general to the degree of anonymous trust, the willingness to enforce contracts, to finance public goods or the social cohesion that exists in a society. It is a relevant variable to assess the economic efficiency and it is closely related to the ability of institutions to establish effective rules. Social capital mainly affects economic activity by reducing production costs in some cases (associated with litigation, security, surveillance, bureaucracy and complexity of contracts, for example) or in others, by easing transactions which would not take place otherwise. Intuitively, social capital may be seen as a catalyst for achieving effi- ciency improvements, or formally speaking, to reach Pareto optimal situations.

The proposed model studies social capital framed as the likelihood of cooperation in a Prisoner’s Dilemma game by applying the concept of psychological equilibrium. Our main results can be summarized in three ele- ments. First, we show that mutual cooperation can be achieved as an equilibrium if perceptions about coopera- tion are optimistic and agents are reciprocal enough. Second, we consider two types of agents, the so called pro- social and the basic one. Then, we introduce the concept of macro-perceptions as the probability that two pro- social players will in fact cooperate when matched. Third, by means of the replicator dynamics we endogenize the distribution of types in the population. The result of it is that when pro-social type agents are able to coordinate themselves on mutual cooperation through favorable macro-perceptions, they are better off than the basic agents and will be the only type of people in the population. In addition, the model characterizes long-run performances under different scenarios and carries out several comparative statics regarding the effects of education or institutional quality on economic performance.

Along with the main findings, this paper provides some original methodological contributions: 1) By means of the concept of psychological equilibrium we split the population into two types of individuals endo- genously―and not as a preliminary assumption of the model. 2) Additionaly, we suggest a way to extend such concept of psychological equilibrium to a dynamic game that through a natural selection process operates over the types previously generated by it. 3) The mechanics of this whole approach leads to the desired outcome of explaining as endogenous variables macro-perceptions and the distribution of types in the population among others.

This paper is organized as follows. Section 2 contains the related literature. Section 3 shows the basic static model structure and preliminary results. The following section describes the dynamic model. Section 5 discusses the main results and their main implications and Section 6 concludes the paper. The appendix contains proofs of the results.

2. Related Literature

There is an extensive and recent literature on the relationship between social capital and economic activity (see for an overview, [1] [2] ). Also, there is a large empirical literature related to the measurement of social capital or the estimation of its relationship to economic activity (see, among others, [3] - [5] ). In this section we discuss the literature close to our model.

Our paper static framework relies heavily on the kindness function and the corresponding psychological equilibrium found in [6] , although we focus on the emergence of types resulting from this setup with the aim of endogenize perceptions, issues that are not considered in [6] . Regarding the dynamic analysis, the closest studies to our model are [7] and [8] , where a similar concept to our macro-perceptions is introduced, although not endogenously as we do. Also, we share with those models that social capital is measured through the proportion of agents that cooperate in a one shot Prisoner’s Dilemma. With a similar goal in mind the model found in [9] explains the distribution of interdependent altruist and spiteful preferences in the population. However, our model does not consider interdependent preferences, hence comparison of results is of little interest.

The existence of moral values is one of the arguments found in the literature of cooperative behavior. This precisely is the motivation found in [10] . This paper studies the evolution of moral values jointly with pure economic incentives when two types of individuals interact (homo kantiensis vs. homo oeconomicus).

Other approaches to study social capital are the following. In [11] [12] we find the basis of the institutional approach to social capital. The argument is that formal or informal institutions―conditioning behavioral rules― may determine collective behavior and individual disposition toward social cooperation. A different theoretical framework is to explain social capital by adopting the theory of networks. Some examples are found in [13] - [15] .

Finally, social capital may be understood as trustworthiness which is the case of our model. This perspective relies on the role of individual beliefs concerning partner’s behavior, and it is generally formalized in a game theory environment, through preference specifications concerning a type parameter.

In [16] the author highlights the natural fact of considering perceptions as a relevant subject when we study- ing social capital. It is also pointed out the need to explain perceptions as an additional endogenous variable of the model. Some attempts are found in the literature regarding the former, but not the latter. In particular, in [17] we can find an example of incorporating perceptions on countries―somehow as a measure of global reputa- tion―to explain international capital flows. The data indicate the existence of a positive correlation between trust-worthiness and investments flows into country. However, in that model, economic variables do not affect perceptions of trust inspired by a country, i.e., perceptions are taken as given in the model. Following the argument of [16] , in our model perceptions are endogenous.

Regarding the dynamic study of social capital there are mainly two alternatives, which are the natural selection and cultural selection approaches. The first one is based on an evolutionary rule that operates on the population that cooperates-usually in an interactive environment which, with appropriate interpretations, most of the time it resembles the Prisoner’s Dilemma game. As a result, this evolutionary mechanism rewards the pro- portion of the population that cooperates through reciprocity. An evolutionary model categorized as institutional approach is found for instance in [20] (see references therein, mainly [12] and [21] ). A key point in this line of literature is the existence of a mechanism punishing those who do not reciprocate. In our paper, we introduce a natural selection approach to study the dynamics of social capital, although we do not introduce any punishment and obtain converge to full social capital under general weak conditions.

In general, the natural selection approach can be summarized as follows. First, the static strategic interaction framework is settled through a sort of Prisoner’s Dilemma. Second, a fitness function to establish whether a type grows or not, is defined-either in terms of the true preferences or in contrast, using some related values. Finally, the analysis of stability is carried out, usually assuming the replicator dynamics. There are at least two interpre- tations of this methodology. First, standard in biology, in which individuals are thought as automata following the precepts of a gene or pool of genes governing their behavior. Second, it is considered that people learn― mainly by imitation―those behaviors that are most successful from among the observable ones. (see among others [22] and [23] ). We choose the latter interpretation for our set-up.¹

Cultural selection is the second dynamic approach to social capital, as described in [24] . Its main idea is to consider the cooperative attitude of individuals as a cultural trait whose probability of being transmitted (from family or society) to descendants is subject to a dynamic rule. The object of study is the dynamics of the pro- bability of a given trait to be present. In [25] this approach is applied to explain the relationship between social capital and economic development.

[16] highlights that perceptions are relevant for a deep understanding of social capital and its relationship with economic activity. This author also points out the need to explain perceptions as an additional endogenous variable of the model. Some attempts are found in the literature. In particular, the model found in [17] considers perceptions on countries―somehow as a measure of their reputation―to explain international capital flows. The data indicate the existence of a positive correlation between trustworthiness and investments flows to a country. However, in that model, economic variables do not affect perceptions of trust inspired by a country. That is, perceptions are taken as given in that paper whereas in our model these are endogenous.

We can summarize that in the previous work of social capital literature more closely related to our research, in general types of individuals are given, perceptions in general are ignored or are not endogenous. Our research allows for a rich interpretation of the aspects that may affect perception and hence social capital as education, information or institutional quality for instance.

3. Theoretical Framework

In this section we introduce basic concepts and micro-foundations of the model in a static setup. Also, we show preliminary results, which provide ground to extract useful implications for the full specification of the model.

We first propose the Prisoner’s Dilemma (PD) game to formalize how social capital is created, economic efficiency and its conflict with individual incentives-as usual in the related literature. The payoff matrix of the PD game is shown next in Table 1.

where, C and D are for Cooperate and Defect actions respectively and 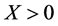is the scale or size of the game. Introducing this variable will lead us to extract some implications of interest. Similar specifications of this game to study the subject of social capital are easily found in the literature―see [18] and [6] for instance.

The utility function that we propose is a convex combination of two elements: a material and a psychological payoff―a specification close to the utility functions found in [19] and [6] . The psychological payoff captures agents’ preference for reciprocity, what is formalized through the interaction of individual kindness functions― to be introduced. In order to define these functions first we need to define some elements and sets.

We define player i’s set of actions as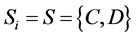; we denote by player i’s action and by player i’s belief about player j’s action―first order beliefs. That is, is what player i believes about player j’s action. Also, denote by 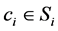player i’s belief about player j’s beliefs about the action chosen by i―second order beliefs. That is, is what player i thinks that player j thinks that he (i) is choosing.

Given the previous elements we define vectors of actions and beliefs. In particular, let be the vector of actions a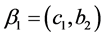nd and, the vector of beliefs of player 1 and player 2 respectively―where 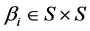for Next, we define the vector of micro-perceptions as Finally, from the previous actions and micro-perceptions vectors we define the Actions-Beliefs (AB) array as

From actions and beliefs we now define the player 1’s kindness to player 2 function. We first consider the set of all feasible payoffs to player 2 for a given first order belief depending on which action player 1 chooses, as Let and Let the equitable

payoff be This element provides a reference payoff level against which

measuring how kind is player 1 to player 2 when choosing. Taking into account these elements, given, player 1’s kindness to player 2 function is given by

Following a similar procedure we construct the player 1’s expected player 2’s kindness to player 1 function. First we consider a given player 1’s second order belief about his own action,. Thus, for a given we consider the set of all feasible payoffs to player 1 that are associated to a particular player 2 expected action b.

Formally, this is the set in which we identify the highest, lowest and equitable

values, denoted by and respectively. Taking into account these values, player 1’s expected player 2 kindness to him is given by

(1)

By operating in a similar manner we define the player 2’s kindness to player 1 function, denoted by, and the player 2 expected player 1 kindness to player 2 function, denoted by.

These kindness functions are used next to define players’ utility functions. We adopt the general framework of the utility function proposed by [19] , although we propose some innovations as shown in the next definition. Agents interaction takes place when each player chooses an action to maximize his utility, which involves taking into account both a material and a psychological payoff. This last element is formalized by each player kindness to the other player when choosing, given the kindness he expected from the other player. In short, the psychological payoff contains kindness functions interaction showing players preference for reciprocity―that is, choosing to be friendly (hostile) when he expects a friendly (hostile) action from the other player.

Definition 1. Players 1 and 2 utility functions are given by the following equations respectively:

(2)

and

(3)

where serves as a weighting parameter for the material payoff,―the psychological size

effect, such that is a decreasing function and The motivation for is

to balance the role of X in both components of the utility function. Although assumptions on are mainly technical, the way we introduce X in the utility function is consistent with related literature suggesting that the size of the game increases the probability of choosing D in the PD or similar games―see [18] or [6] .

Next we define the equilibrium concept linked to the utility function just considered.

The Action-Beliefs vector where is a Psychological Equilibrium (PE) if

1) for all.

2) for all.

3) and.

Conditions 1) and 2) establish that the pair of actions is a Nash equilibrium given the exogenous beliefs vector, while condition 3) implies that beliefs should be consistent with actions in the PE.

It is convenient to remark that since beliefs are exogenous within the definition of PE, it might be tempting to think that the concept of PE barely contribute to explain the relationship between beliefs, actions and economic performance. Nevertheless, this is a first step in the development of the model, and once it is fully specified, beliefs will become endogenous. Hence, within the dynamic aggregate setup, we will be able to describe how beliefs affect actions and economic performance in the long run and vice versa.

Preliminary Results

We are now in conditions to identify the PE actions-beliefs vectors in a psychological PD game as well as to show related implications. Since condition 3) is to be hold by a PE, only some AB vectors are to be considered. Let the following AB vectors and be the set of feasible PE candidates, as only for them, hold.

Before formally showing the existing PE, it might be convenient to show in an example the total payoffs matrix of the psychological game for a given micro-perceptions vector. This exercise may illustrate the concept and identification of the existing PE. Taking micro-perceptions as, since for all it is possible to compute player 1 utility level for all possible action pairs from player 1’s utility function. The resulting total payoffs matrix of a psychological PD given is shown in Table 2. Only player 1’s payoffs are shown since the game is symmetric and we assume so far that parameters are the same for both players.

A psychological equilibrium is a Nash equilibrium of the psychological game generated by a given micro- perception vector. Hence, for our example, to identify a PE we just need to prove that a pair of actions is a Nash equilibrium using Table 2 information. It is of course of interest to find out whether the pair of actions could be a Nash equilibrium under certain conditions. Since variations of material and psychological payoffs have opposite sign when player 1 deviates from C, the pair of actions would be in fact a Nash

equilibrium depending on and X.

We show next a full formalization of the existing PE generated by the psychological game, for the set of all possible beliefs which are consistent with the AB vectors of interest. For a clear understanding of the next result, we consider the possibility of different player specific values for the parameter, where denotes player i’s parameter value, for

Proposition 1. Consider the utility functions given in Definition 1. Then:

1) Neither nor can be PE;

2) For any with, is a PE;

3) Taking

(4)

then: 1) If with or, is the unique PE; 2) If with, (and) is a PE.

4) is decreasing in X and

The proof can be found in the Appendix.

Some interpretations and implications of interest come out from the proposition above. Items 1), 2) and 3) imply that there are only two PE: and. Thus, adding a psychological term to the standard utility function allows to achieve the cooperative solution in a PD game under certain conditions. On the other hand it is worth saying that by construction, one or another PE is to be achieved depending on the micro-perception vector considered by each player, as well as on the value of the parameter. In particular, is achieved if and only if and for all If for or, then is the unique existing PE, and obviously it is achieved if.

Although a relative low weight to the material payoff is needed in order to achieve the cooperative PE, item 4) shows that such weight has to decrease if the size of the game, X, increases. In other words, the higher the economic transaction in hand is, the lesser has to be to achieve the cooperative PE.

So far this static framework relies closely on the [6] model so the previous result can be easily derived from it. However, it was needed to state it properly for the sake of the forthcoming development of the model. In particular, we draw one important implication from Proposition 1 which is the following. Given X, the critical value leads us to consider two types of agents within the population. On the one hand, those whose parameter is and on the other hand, those characterized by the parameter value These are called the pro-social type and the basic type respectively.

4. Aggregation and Dynamic Setup

In this section we describe the aggregated economy and its dynamic behavior. Aggregation is modeled using a structure close to that of the overlapping generation models, in an infinite periods horizon where time is a discrete variable. Thus, in each period a new generation is born, each individual living two periods. As previously mentioned, there exist two types of individuals, called pro-social and basic types, denoted as and respectively.

We propose the replicator dynamics approach for the determination and evolution of types.² Roughly, this general mechanism operates as follows: during the first period of life each individual acquires his type (either in a biological sense or in a learning interpretation of the process) for his second period of life. The acquired type by this evolutionary process is the one that belongs to the group with a higher level of expected utility than the average expected payoff of the population. Because of that, the group of individuals of this type increases within the population at expenses of the other groups.

For simplicity, we will assume that only PE, that is, or are achieved through strategic interaction and that there exist perfect information on types.³ Once the type is acquired, players are randomly matched and interact in the framework of the psychological game described in the previous section, where macro-perceptions will play a crucial role to determine simultaneously micro-perceptions and actions. The process thus described continues period by period through generations, until the proportion of individuals of each type reaches a steady state under the conditions that we consider.

4.1. Dynamic Analysis

First, we introduce new notation in order to define the fitness function to carry out the dynamic analysis-recall that only PE are achieved through the game. Let represent the utility level of a type player, conditioned to beliefs for. Similarly, is the utility of a player of the same type conditioned to beliefs for. Finally, denotes the utility level of a type player.

Let be the proportion of type players in the population at period t. Let and be the expected utility for types and players respectively at period t. Finally, the average utility of the game is.

The process governing the evolution of is the Replicator Dynamics, given by the following equation:

(5)

The Replicator Dynamics generates the same steady states and stability as any other sign preserving dynamics (see, for instance, [36] ), which we define as follows. A dynamic process― where F is a continuous function in all its arguments―is a sign preserving dynamic if .⁴ Since there are only two types of individuals within the popu- lation, when, the previous condition is equivalent to

(6)

For simplicity we assume that follows a sign preserving dynamics hereinafter.

The purpose of our dynamic analysis is to identify the steady states for and study their stability. A steady

state is a sequence such that for all. Considering equation (6) we only need

to know the sign of in order to conduct the dynamic analysis. Thus, if , increases (decreases) over time. Finally, if then remains constant-which is the steady state condition.

Given the previous argument we need to study the condition for identifying the steady states values. The computation of is immediate, as type players only choose D, hence only the PE will arise regardless of the type of his opponent. Formally,

(7)

The computation of is not so trivial, as type players can achieve any of the existing PE. A player of this type will meet a type player with probability―hence the only achievable equilibrium is―and obtain a utility level On the other hand, a type player would meet a player of his same type with probability. In this case he faces a dilemma generated by the existence of two feasible beliefs vectors―which conditioned his behavior and thus the achievement of or. Thus, it then comes up as a natural question which beliefs vector players are going to choose.

4.2. Macro-Perceptions

Given the need to provide a satisfactory answer to the coordination problem found in a type players matching, we introduce the concept of macro-perceptions. The intuitive argument behind this concept is quite simple and a standard one in the economic literature. In short, we solve the mentioned problem by assuming that type players share a common perception about the probability of coordinating their actions. Next we provide a formal definition of this concept.

Definition 3. Given a population in which the proportion of pro-social people is, we define macro- perceptions through the continuous function which for an entrant pro-social player measures the conditional probability of achieving, given that he is matched to another pro-social player. The function satisfies the following assumptions: and is increasing in.⁵

Some comments are in order. First, note by definition measures the probability of a new entrant pro-social player of achieving. That is, in a society where is the proportion of pro-social people, micro- perceptions leading to occur with probability. Second, it would have been sufficient to just require continuity on and nothing else. Nevertheless we have imposed two more assumptions―in- creasing and―for simplicity.

From the definition of macro-perceptions we can now compute the expected utility of a type player, which is,

By rearranging terms properly in the previous equation, we have,

(8)

where Equation (8) is consistent with the definition of, since for a type player, micro- perceptions leading to C occur (and PE is achieved) with probability and also those leading to D occur (and PE is achieved) with probability. Note that that is, for a type player, the probability of achieving the PE is larger than the probability of matching another player since not only this type leads to such PE.

Taking into account Equations (7) and (8), we are now in condition to compute the difference. Thus, by substituting the considered equations, we have

(9)

The steady states for are found by setting equation (9) equal to zero. In the next section we conduct the full dynamic analysis. It is important to remind for further interpretations the meaning of in equation (8), as this value is related to the probability of convergence to the full social capital situation.

5. Results

In this section we present the main results of the model: identify the steady states and discuss convergence to the optimal steady state under different set of assumptions. Overall, our main achievement is that we explain endogenous and simultaneously social capital, economic performance, micro and macro-perceptions.

Proposition 2. Consider the dynamics given in (6). Then:

(a) If then there exist only three steady states: and,

such that where Also, and are asymptotically

stable and is unstable.

(b) If, then only two steady states exist: and, and for all, converges to.

The proof can be found in the Appendix.

Item (a) shows the most favorable conditions for convergence to full social capital. The interpretation of the assumption stated in (a) is simple. First, if―say the cooperative condition henceforth― does not hold, it would be difficult to observe convergence to, since each one of the terms in that inequality is associated to the expected utility of the corresponding type.

We require to be an increasing function on. See that in this case there exists a unique root for equation in―which is a less restrictive condition. Nevertheless, we impose increasing for simplicity. In any case, assuming that only one root exist in is an extension of the focal point argument used in coordination games (See [37] ). Indeed, the cooperative equilibrium works as a focal point, thus the more pro-social people there are in the society, the more attractive the cooperative equilibrium is, and the more likely it is to coordinate in that equilibrium.

If the cooperative condition do not hold, convergence to full social capital fails, as shown in (b). In intuitive terms, full social capital is not reached in the long run if the probability of cooperation between pro-social players is too low or if the return of cooperation is not high enough.

The following graph (vs., generated by the Replicator Dynamics) shows the dynamics of variable for the cases (a-i) and (b) of Proposition 2. The case (a-i) corresponds to the existence of an interior steady state. If for the initial condition the economy converges to in the long run. In case (b), there is no interior steady state, thus the economy converges to (see Figure 1).

To conclude, recall that is the probability of occurrence C, so the item (a-i) of Proposition 2 allows us to interpret as the lower bound of the probability of achieving C so that the economy converges to in the long run. The intuition of the above argument is that people turn out to be individually cooperative (i.e. is high enough) when they perceive themselves in such a way that as a result of their behavior, the proportion of pro-social players increases. In other words, an individual will cooperate when by choosing “cooperate” it is likely to achieve cooperation, or in other words, when he perceives that himself belongs to a sufficiently large group. So, because of this perception of himself, and thus that cooperation was achieved, the proportion of pro-social players increases and the economy converges to. This argument leads us to interpret informally as a measure of the degree to which people perceive themselves as addable or member of a group in which their contribution is effective.

Before presenting some implications, it is worth to establish the precise conditions under which the co- operative condition (CC) holds.

Proposition 3. Consider the two types of agents given by the previous proposition, characterized by and

. Then―the CC―is satisfied iff.⁶

Proof follows from algebraic manipulations and hence omitted.

The CC says that pro-social playing are better off than basic type people if and only if basic people are not too materialist―in relation to pro-social people―, that is, if and only if.

We can easily prove that for, and that is always larger than

one. Therefore, the CC and the requirements are not inconsistent if, for instance

, which holds if and only if is large enough. Observe, furthermore, that if, then can be arbitrarily close to one, without violating any condition. In particular,

if is sufficiently small but not too small, the larger is X, the larger is, and therefore the larger can be, without violating the CC.

Comparative Statics

Previous results allow to discuss the effects of exogenous changes in, X or on the probability of convergence to steady state (value that may be estimated by). These implications could be useful to explain some empirical regularities concerning corruption or institutional quality and its relationship to economic performance. The proofs are given in the appendix.

First we highlight some previous conclusions drawn from Proposition 2 when the CC holds. In this case, we show that there exist convergence to if and only if the initial condition is such that

Thus, if, there would be no convergence to but to

and because of that, the larger is the lower the probability of achieving convergence to. Finally, note that under the conditions stated, there exist a positive relationship between and. Thus, considering two interior steady states and such that and

, if, then since is increasing.

Corollary 1 ($_D$ increases). If, , and is increasing, then there exist a negative relationship between and the probability of convergence to.

To highlight the idea of this corollary, it may be useful to assume that, as in this

case can be arbitrarily close to one. Indeed, in this last case, the graphical representation of the result in the space (vs.) would show that the inner root shifts to the right as increases, up to some limiting value smaller than one. Since the probability of convergence to the optimal solution is we conclude that there is a negative relationship between such probability and this and.

In intuitive terms, this corollary may explain the paradox of individuals weighting to high the material payoff, and by doing so penalize individually and collectively the options to achieve the best material results.

Corollary 2 ($X$ increases). If CC hold, , is increasing and is large enough

(), then, if X increases, as decreases, the probability of convergence to the steady state

increases.

We show in Section 3, that as X increases, the interaction leads eventually to the non-cooperative equilibrium, which in dynamic terms means that there is convergence to the steady state. However, it is possible to find convergence to if parameter is not too small or r is large enough. The intuition is that provided r is large enough, then, the negative effect of large X not only disappear, but also become positive. That is, if the reward for achieving cooperation is high enough, then it overtakes the negative effect of a large X, so that the larger is X, the larger the probability of convergence to full social capital state.

Corollary 3 ($$ shifts). If CC hold, and increasing, then societies with a higher level of optimism about anonymous cooperation, converge with higher probability to the optimum steady state. Similarly, societies with lower optimism converge with higher probability to the inefficient steady state.

We can consider that the level of optimism about the anonymous cooperation could be measured by macro- perceptions function,. Thus, an increase in the level of optimism would shift the function upwards for a given, which imply that decreases and therefore that the probability of convergence to increases.

Some variables that could affect that level of optimism about anonymous cooperation may in general be related to institutional quality, as corruption, democratic participation, transparency in the financial sector and the legal system guarantees, or mass media political power, for instance. These variables may be formalized through macro-perceptions in our model. So, if there is a shock related to those variables, it would be under- stood as a shift in the level of optimism about the anonymous cooperation, which in our model is formalized through, hence affecting the probability of convergence to.

6. Conclussions

In this paper we have proven that provided that the CC is satisfied two variables are crucial in order to obtain full social capital in the long run, the macro-perceptions and the proportion of pro-social people in the society. That is, if two societies only differ in macro-perceptions, the will not reach the same distribution of types and economic outcome in the long run. In fact, that with optimistic macro-perceptions will achieve better economic performance. These results beg the natural question of how to change macro-perceptions.

This is a complex issue indeed although some considerations are in order. Formal and informal education is one of the main sources of perception on trust. Specially informal education is relevant as people tend to imitate or learn successful behavior, which in our model is captured by the fact that the dynamic process is understood as a learning process. People tend to imitate, then to learn, successful behavior, so it is important to observe which in particular is the successful behavior. On the other hand, we cast doubt on how strongly formal education may help to increase social capital. Moreover, we conjecture that the effect of formal education over social capital is much lower than the effect of the imitation process, an issue that is left for future research. Finally, it may be relevant for institutions to establish effective rules to control the influence of lobbies on mass media and also on political actors.

Cite this paper

José A. Hernández,César Guerrero-Luchtenberg, (2016) Social Capital, Perceptions and Economic Performance. Theoretical Economics Letters,06,214-227. doi: 10.4236/tel.2016.62024

References

Appendix

A.1. Proof of Proposition 1

First we prove (a). Consider and the player 1. We will show that a deviation from playing C is advantageous to player 1. Imagine player 2 chooses D, and player 1 chooses C. Recalling that

, and noting that

, and we have that both terms of, the

psychological term and the material term, increase

if it chooses D. Indeed, , and

, due to,

and. An identical reasoning can be made for and player 2. Therefore the item (a) is done.

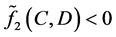
The proof of (b) is analogous to (a) and hence omitted (both parts of the payoff decrease by playing C against D).

In order to prove (c) we consider player 1, rename for practical purposes as (recall that), define, and finally define the function as

Thus, we have that is not a PE if and only if, and that is a PE if and only if (if we assume that when, the cooperative equilibrium holds ). Now notice that is a linear function of and thus it is enough to show that and and take such that.

We have that so that; on the other hand,

and, thus

. Now, we have that

, and

, thus.

Thus,

(10)

and hence, if, and beliefs are, then C is a best replay to C. The same reasoning applies for the player 2, and thus the item (c) is done.

The proof of (d) is a direct consequence of being decreasing and, since any function

of the form with is increasing.

A.2. Proof of Proposition 2

First, we prove (a). To see and are steady states, notice that if, then by definition of the dynamics, and the same reasoning applies for (the other type).

For the rest of the items, as now we are looking for interior steady states, we notice that is an interior steady state if and only if, where given by

(11)

where and

. Thus,

. Then, to see that there is only one non-trivial

steady state, it is enough to show that has only one root in the set. Indeed, as is an increasing linear function in, we have that satisfies if and only if (with, since we must have), and as has only one solution by

hypothesis, then has only one solution, which is denoted by and satisfies.

Finally, to see that and are asymptotically stable, due to that is continuos, it is enough to show, and and that is the case as and

. Indeed, we have that for all, since is increasing, due to that is increasing; thus if (, the initial condition of the system), is strictly decreasing and then tends to some; now, again due to that is increasing and continues, we must have; indeed, recalling that we defined in Section 4 the general dynamic rule as

, where F is continuous in all its arguments, we must have

, and thus must be a steady state, what is impossible if, due to that and is increasing. Similarly, we have that for all for all, and hence if, we have that tends to one as t tends to infinite. Consequently, is unstable. The item (i) is then proven.

Now we come to the item (b). Notice that if, then, and therefore for (as, for), and thus there are no interior steady states, and for all, tends to zero as t tends to infinite. Also, if does not have roots in, then for (recall that), and therefore the same reasoning as before applies.

A.3. Proof of Corollary 1

Taking into account that, it can be seen that is a linear function

of, with positive slope. Then, if increases, increases too, and as it was shown in Section 5 were we presented the results, decreases.

A.4. Proof of Corollary 2

First, it can be easily checked that With this in mind, the proof of this corollary is similar to that of Corollary 1. Simply notice that that if, then as X increases, and

decreases and thus increases.

A.5. Proof of Corollary 3

Let Q represent institutional quality for instance and consider that for all Thus,

, and then Since is in-

creasing, we have that what proves the first part of the corollary. The second part is totally analogous to the first one, and hence omitted.

NOTES

¹Possible Darwinian causes for cooperation has been observed in biology (see [26] ), among which it is worth to mention: 1) Genetic kinship, as for example, suicide bees. See [27] - [29] ); 2) Reciprocation, as found in symbiosis (or in vampire bats, for example). See [30] and [31] ; and 3) The benefit of conspicuous generosity, as a way to signal the true type, as the case of the Arabian babblers (see [32] - [35] ).

²Although the proofs are done using the sign preserving dynamics, a more general form of dynamics.

³It would be relevant to consider also and, either by allowing basic type players to cheat a pro-social one or simply as a result of an error in micro-perceptions. Nevertheless, the model becomes more complex and does not provide new insights on what we already have.

⁴It is easy to check that this equation implies that if and only if, except when. If we impose That is, a type cannot emerge if it did not exist previously.

⁵There is no need to impose any condition on, except being a well defined number.

⁶The inequality only is possible if. If, the Cooperative Condition is not satisfied.