Theoretical Economics Letters
Vol.05 No.04(2015), Article ID:58814,9 pages
10.4236/tel.2015.54062
Trends of Base Metals Prices
Nguyen Bao Anh, Aggey Semenov
Department of Economics, University of Ottawa, Ottawa, Canada
Email: bao-anh.nguyen@uottawa.ca, aggey.semenov@uottawa.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 July 2015; accepted 11 August 2015; published 14 August 2015
ABSTRACT
The real price of base metals exhibits a decreasing trend over time. We model base metals prices as the equilibrium of aggregate supply and demand. This allows us to study the effect of determinants of base metals prices. The trend in the price of base metals depends on technological progress, resource scarcity, natural resource taxes, and the interest rate. Under certain parameter restrictions we can explain the decreasing trend in prices over time. This phenomenon is mostly explained by the substitution effect and technological progress. We derive policy implications related to natural resource taxation.
Keywords:
Base Metals Prices, Price Trends, Historical Price, Mining, Metals Industry, LME, CRS

1. Introduction
Base metals are industrial non-ferrous metals: aluminum, copper, lead, nickel, tin, and zinc. They are used for building homes, automobiles, plants, equipment, pipes, wires, and so on. Such extensive use of base metals in industry inevitably links base metals markets to economic conditions. An article in Investopedia by Mark Riddix states that “Investors who want to know where global economies are headed should keep an eye on base metals”. Figure 1 presents the dynamics of base metals prices from 1967 to 2002. There is a clear downward trend of prices of almost all base metals.
In this paper we study the determinants of trends in base metals prices. For the supply side we consider the regulated industry with a Cobb-Douglas production function for base metals. By solving the Hotelling-style problem of the regulator we find that the trend in the supply of base metals depends on natural resource tax, interest rate, technology progress and degradation of ore in nature. Under a constant return to scale (CRS) production function the supply of base metals is perfectly inelastic. Importantly, the supply is decreasing over time for realistic values of parameters. We then study the demand for base metals from the manufacturing sector. The resulting demand is also decreasing. Thus we can justify the possibility of a downward sloping price trend.
Figure 1. Relative price of base metal over time, Krautkraemer (2005).
The model incorporates the following features of base metals: 1) Base metals are recyclable, and the portion of recycle materials is constant over years; 2) Producers’ incomes vary with the content of base metals distributed in the Earth’s crust; 3) Deposits are common in nature and inexpensive to access; 4) Prices show positive cross-elasticities of demand; 5) Deposits are homogeneous products, durable for storage. Our results are driven by the use of the Cobb-Douglas function for base metals production1. The use of this production function reflects substitutability between inputs, particularly between capital and mineral deposits, which are degrading over time―thus making the use of capital more efficient. [1] - [3] point out that the decline in the mineral resource intensity of mining production provides evidence of the effect when the costly input (mineral deposits) is substituted by the less costly (capital), given technological progress. For example, the solvent extraction- electrowinning (SX-EW) method for refining copper ore succeeded in reducing costs. This method allows the more efficient use of lower grade copper ore.
Literature Review
Despite the important role of base metals in the world economy there is little research on pricing. Our paper fills the gap in this literature by offering a theoretical treatment of pricing which includes the production functions for metals, manufacturers, and the set of technological and policy-relevant parameters which affect the price trend.
Theoretical Hotelling-style models predict an increasing real price for non-renewable natural resource commodities. However, empirical observations establish falling prices for these commodities ( [3] and [4] ). To explain this inconsistency, [5] suggested a U-shaped time path for relative prices. However, [4] pointed out that there is no evidence of increasing base metals prices. He concludes that technological progress has ameliorated the scarcity of natural resource commodities, but resource amenities have become more scarce, and it is unlikely that technology alone can remedy that. Building our first part on the works of Slade we go further by introduc- ing the Cobb-Douglas production function, which combines the effect of technological progress with the notion of substitutability of inputs. This allows us to establish the possibility of a constant declining trend of prices.
2. The Model
The regulated industry provides the supply of base metals. The regulator maximizes the discounted difference between revenue
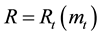 and the total cost of production of the industry
and the total cost of production of the industry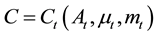 . The extraction path of the mining industry reflects the degradation of metal minerals in the deposit. The quality of ore at time t is
. The extraction path of the mining industry reflects the degradation of metal minerals in the deposit. The quality of ore at time t is
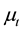 (the content of metal minerals in extracted ore). Degradation of the quality over time assumes
(the content of metal minerals in extracted ore). Degradation of the quality over time assumes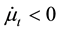 . The regulator chooses the time path for the extraction rate
. The regulator chooses the time path for the extraction rate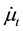 . We consider the Cobb-Douglas production function for metals:
. We consider the Cobb-Douglas production function for metals:
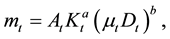 (1)
(1)
where
 is capital,
is capital,
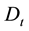 is mineral deposits, and
is mineral deposits, and
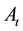 represents the total factor productivity of the mining industry2. We denote by r the cost of capital and by
represents the total factor productivity of the mining industry2. We denote by r the cost of capital and by
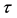 the natural resource tax.
the natural resource tax.
Demand for base metals comes from the manufacturing sector. The manufacturing sector has a Cobb-Douglas production function
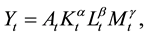 (2)
(2)
where
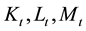 are capital, labor, and base metals demand at time t respectively. We assume the CRS production function for the manufacturing sector
are capital, labor, and base metals demand at time t respectively. We assume the CRS production function for the manufacturing sector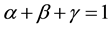 .
.
3. Equilibrium
3.1. Supply
The industry’s cost minimization function
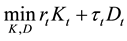
Using standard technique we obtain the following:
Lemma 1―The cost function of the mining sector is

where
Proof: see Appendix 5.1.
After extracting ore from the deposit, the minerals are separated from ore by the benefaction process. Smelters produce base metals from refined minerals. Production output




The regulator maximizes industry profit by choosing the extraction path. By (4) it is equivalent to choosing the rate of ore degradation
Solving the maximization problem yields the following (we denote by

Proposition 1
1) The (inverse) supply function for base metals from the mining sector is


2) If a + b = 1 then


Proof: see Appendix 5.2.
The following Corollary follows from Proposition 1:
Corollary 1
1) The price elasticity of supply is

2) If a + b = 1 then the supply of base metals is perfectly inelastic.
Proof: see Appendix 5.3.
In (9),




Evaluation of the returns to scale in metals production is a difficult task. We follow a somewhat implicit method to justify the constant returns to scale hypothesis. Empirically, [6] finds that the price elasticity of base metals is between 0.2 and 0.8 (Aluminum 0.7 - 0.8; Copper 0.4; Lead 0.2; Tin and Zinc 0.2 - 0.4). Based on these estimations we assume that metals production has constant returns to scale. Thus we can focus on Equations (7) and (8) to explain the determinants of the Hotelling pricing rule:
1) High total factor productivity and good quality of ore in nature keeps the supply of base metals relatively low;
2) The growth rate of technology

3) The degradation progress of ore in nature

To simulate the time path of supply consider the values


Now considering the parameters of the economy


Proposition 2
Proof: Immediate from (7) and (8).
There are several policy implications from Proposition 2: 1) If the natural resource tax

These results depend on the assumption of a Cobb-Douglas production function. According to the Inter- national Council on Mining and Metals [7] , most of the mining productivity increases in the past century have been achieved through the use of more efficient processing of lower grade ores and the use of larger scale equipment. Most ore grades show a gradual decline over the period of available data, except for Canadian Zinc and Nickel grades5.
3.2. Demand
The demand for base metals comes from the manufacturing sector. Rewriting the production function (2) in per- capita form we have

Lemma 3
1) The (inverse) demand function for base metals from the manufacturing sector is

2) The price elasticity of demand is

3) The rate of change of


Proof: see Appendix 5.4.
Equation (11) implies that ceteris paribus: 1) Technological progress reduces the demand for base metals; 2) Economic growth and interest rate increase the demand.
The expression (12) decomposes




Equation (13) implies that technological progress has a positive impact on the rate of change of



In the long run the capital growth rate equals zero in the steady state:




3.3. Equilibrium
To see the trend of equilibrium price we present supply and demand in the three-dimensional coordinate system

The Figure 1 is a projection of Figure 2 into





Figure 3 shows relative prices and trends of Aluminum, Copper, and Nickel from 1900-2012 in 1998 US$9. These trends illustrate our findings.
Figure 2. Aggregate supply and demand equilibrium.
Figure 3. Relative price of base metals over time, USGS.
Notice that the prices of Aluminum and Copper spike during World War I (1914-1918). The price of base metals in periods of economic crises during the 1930s and in 1996 was below trend. During the financial crisis of 2007-2009 the prices of almost all base metals were highly volatile which was depicted clearly and explained in [9] .
4. Conclusions
The theoretical literature has no comprehensive consideration of all relevant factors that impact the price of base metal. Normally the price is defined only by the mining industry [5] . Market demand and participation of speculative traders in commodity exchanges are not considered.
This paper answers the question what drives the trends of base metals prices. By modeling the industry regulator’s problem for extraction of base metal minerals in combination with the demand from the economy, we show that in the long-run the price of base metals is a function of total factor productivity of the mining industry, the availability of metals in nature, natural resource tax, interest rate and demand from economy. We decompose the price elasticity of supply and demand into responsiveness of price to changes of price determinants. Assuming constant returns to scale, the price elasticity of the supply of base metals is relatively small (
Acknowledgements
The authors thank Zhiqi Chen, Jean-Francois Tremblay, Gamal Atallah for careful reading of the manuscript and many helpful comments. Our sincere thanks go to Margaret Slade, Nguyen Van Quyen for useful suggestions and David Stambrook for extensive discussions. We also thank participants of CEA Annual Conference at Ryerson 2015 for comments and suggestions. The paper is a part of a bigger project: “Trends and Fluctuations in Base Metals Prices”, which is awarded the prize for the best paper at Vietnam Economist Annual Meeting 2015 in Thai Nguyen City, Vietnam. The authors thank SSHRC for financial support.
Cite this paper
Nguyen BaoAnh,AggeySemenov, (2015) Trends of Base Metals Prices. Theoretical Economics Letters,05,531-540. doi: 10.4236/tel.2015.54062
References
- 1. Tilton, J. (1989) The New View of Minerals and Economic Growth. Economic Record, 65, 265-278. http://dx.doi.org/10.1111/j.1475-4932.1989.tb00935.x
- 2. Tilton, J. and Landsberg, H. (1999) Innovation, Productivity Growth, and the Survival of the US Copper Industry. Productivity in Natural Resource Industries; Improvement through Innovation, 109-139.
- 3. Bunel, M. (2001) Estimating the Effects of Technology and Depletion on the Real Price of Copper in the U.S. Using a Cointegration Approach. Working Papers on Environment and Economics.
- 4. Krautkraemer, J. (2005) Economics of Natural Resource Scarcity: The State of the Debate. Resources for the Future Discussion Paper, 5-14.
- 5. Slade, M. (1982) Trends in Natural-Resource Commodity Prices: An Analysis of the Time Domain. Journal of Environmental Economics and Management, 9, 122-137. http://dx.doi.org/10.1016/0095-0696(82)90017-1
- 6. Stuermer, M. (2014) Industrialization and the Demand for Mineral Commodities. Working Paper, Federal Reserve Bank of Dallas, 1413.
- 7. ICMM (2012) Trends in the Mining and Metals Industry. ICMM Report. http://www.icmm.com/document/4441
- 8. Mudd, G. (2009) Historical Trends in Base Metal Mining: Backcasting to Understand the Sustainability of Mining. Proceedings 48th Annual Conference of Metallurgists, Canadian Metallurgical Society, Sudbury, 2009 August.
- 9. Nguyen, B.A. and Semenov, A. (2015) Fluctuations in Base Metals Prices. Theoretical Economics Letters, 5.
5. Appendix
5.1. Proof of Lemma 1
The cost minimization problem is


Ignoring subscript t and solving (15) for D we have

Substituting (16) into (14) yields

The first order condition is
Thus we obtain the conditional demand function for K

The conditional demand function for D is

Substituting (18) and (19) into (14) yields the cost function of the industry
Finally denote

5.2. Proof of Proposition 1
The Hamiltonian is
where


The derivative of revenue equals to the price of base metals

The price change over time is the derivative of p with respect to time (we ignore superscript s)

The derivative of


Substituting (22) into (21) and rearranging the RHS yields

Considering the cost function in Equation (3), in case of non-CRS, or


Assuming a constant returns to scale production function

We obtain:



Substituting (27) and (28) into (23) yields
Substituting (26) into (20) yields
5.3. Proof of Corollary 1
Taking the logarithm of both sides of (24) yields

Differentiating both sides of (29) leads to

Dividing both sides of (30) by


Note that

5.4. Proof of Lemma 3
We have

The inverse demand function is

Taking the derivative of p with respect to time yields

Dividing both sides of (35) by (34) we obtain (13). Finally (12) can be obtained as in the proof of Corollary 1 above.
NOTES
1In a companion paper “Fluctuations in Base Metals Prices”, we study non-systematic price determinants. The model used there is very different and has little overlap with the model in this paper.
2We do not include recycling into the production function of metals. According to the International Copper Study Group (ICSG), recycled content in copper production has remained steadily in the 33.7% - 36.8% range over the last decade. The International Zinc Association states that 60% of zinc production comes from mined ores and the rest from secondary materials. The Yale University Center of Ecology reports that the recycling input rate of nickel production is 33%. The International Lead Association says that the recycled content of production is 52.6%. In general those figures have remained stable over the last ten years (Metal Bulletin 30 January 2012, Report of the United Nations Environment Program 2011). Thus we assume a constant share of recycling in metals production.
3The degradation progress is the reduction of base metals content


4http://www.worldbank.org/; http://www.adb.org/; ICMM Report October 2012.
5The trends over time for ore grades in Australia, Canada, and the USA are shown in [8] .
6http://www.worldbank.org/; http://www.adb.org/
7http://www.economist.com/blogs/graphicdetail/2012/10/daily-chart-4?fsrc=scn/tw/te/whatcrisis
8Empirical works in literature estimate that

9We thank Margaret Slade for suggesting the availability and sources of historical data.




















