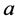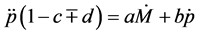Theoretical Economics Letters
Vol.04 No.08(2014), Article ID:50727,4 pages
10.4236/tel.2014.48088
A Note on Price Asymmetry Using a Monetary Model
Pablo L. Schiaffino1, Juan Pablo Pinasco2
1Facultad de Ciencias Económicas, Universidad de Palermo, Buenos Aires, Argentina
2Facultad de Ciencias Exactas, Universidad de Buenos Aires, Buenos Aires, Argentina
Email: plschiaffino@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 August 2014; revised 2 September 2014; accepted 8 October 2014
ABSTRACT
In this paper we present a macroeconomic foundation of downward money price inflexibility based on classical Monetary Economics. We show that under the principle of risk aversion and the neutral money axiom, our model derives an endogenous asymmetric price response as prices adjust more rapidly when they go upward than downward. This asymmetry does not disappear; on the contrary, it is increasing in time.
Keywords:
Price Asymmetry, Monetary Model, Sticky Prices, Classical Economics

1. Introduction
The literature of asymmetrical price adjustment, both theoretical and empirical, is large ([1] who offer an extensive comprehensive survey). For modern new Keynesian macro, the whole point was analytically to develop microfoundations to justify the existence of price asymmetry or sticky prices. Others theoretical models combined this microeconomic foundation with the strategic interaction factor in order to generate price asymmetries during the adjustment process [2] -[4] . Different kinds of models were built to show up price asymmetries.
In this long list there wasn’t, however, a macroeconomic foundation of downward money price inflexibility based on classical Monetary Economics as it is presented in this note. Here, we assume a money demand where agents are risk averse. The conclusion derives an endogenous asymmetric price adjustment as prices adjust more rapidly when they go upward than downward. We analyze price reaction around a neighborhood—at a starting price equilibrium—after we modified the money supply (hence the neutral money axiom holds since prices movements are caused by changes in the quantity of money). This result does not disappear at the second order; on the contrary, it intensifies.
We work with a standard Monetary model that builds on the same model that J. H. G. Olivera [5] used to study how prices adjust to its equilibrium value, but we reconstruct Olivera’s approach in order to analyze how prices behave under changes in the monetary supply. First, we show a first-order effect that the price adjustment process when the quantity of money varies is heterogeneous—a result more or less present in Olivera’s model. Second, we show a second-order effect that the initial price asymmetry tends to increase as time goes by a simple but a definitely new innovation. We reconcile this result with some previous empirical and we discuss the essence of this asymmetry arguing that there is an economic intuition behind this result not only a mathematical truth.
2. The Model
The starting point is the classical conception that prices fully adjust according to money supply variations:
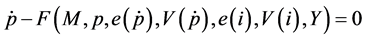 (1)
(1)
where 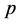 is the price level,
is the price level, 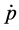 is the price time derivative,
is the price time derivative, 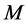 is the nominal money supply,
is the nominal money supply,  is the real interest rate,
is the real interest rate, 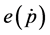 and
and 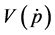 are the mathematical expectation and the volatility level of the price variation respectively, while
are the mathematical expectation and the volatility level of the price variation respectively, while 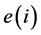 and
and 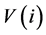 are the mathematical expectation and the volatility level of the real interest rate. Finally,
are the mathematical expectation and the volatility level of the real interest rate. Finally, 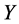 is the real national income. We define
is the real national income. We define 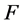 as the excess money supply function (EMSF), which according to traditional assumptions, varies positively with the nominal money supply.
as the excess money supply function (EMSF), which according to traditional assumptions, varies positively with the nominal money supply.
The EMSF also varies negatively with the price level and positively with expected prices and price volatility. These two assumptions typically capture the reaction of money demand under expected price change and its corresponding volatility. From now on, we concentrate on money variations and its impact over the price dynamic adjustment; hence we assume that 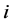 and
and 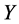 are fixed and remain constant over time.
are fixed and remain constant over time.
 Proposition 1: Suppose that
Proposition 1: Suppose that 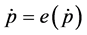 and
and 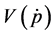 is a strict increasing function of
is a strict increasing function of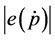
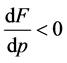
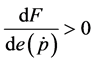
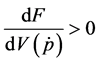
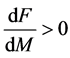
the quantity of money.
Proof. Recall we assume that 
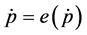
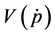
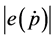
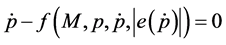
Let’s define an equilibrium value for price as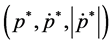
quantity of money at this point is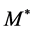
quantity of money around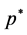
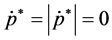
proximation of equation (2) can be expressed as:
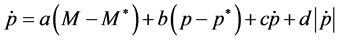
where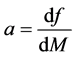
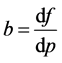
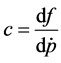
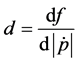
constant. Notice that the sign that accompanies the term 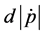
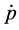
show in the next lines1. Equation (3) can be re-written as:
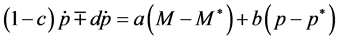
Or,
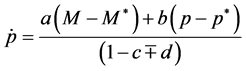
If prices are initially at equilibrium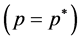
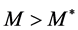
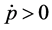
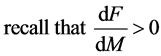
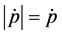
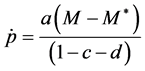
Conversely, when 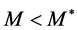
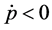

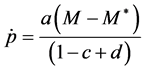
From equations (3.3) and (3.4), it is immediately inferred that upward price adjustment is more rapid than downward price adjustment when the quantity of money deviates from its equilibrium value.

Proof. The corresponding Taylor series for price at 
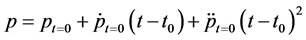
where at 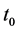
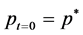
equation (4) depends, among other things, on the value of 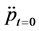
tion (3) in order to get the second order time derivative at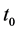
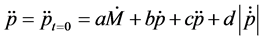
where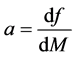
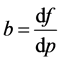
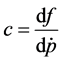
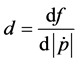
that accompanies the term 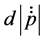
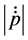
From here, two cases arise. The case when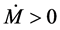
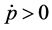
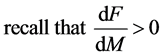
therefore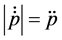
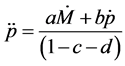
Conversely, when 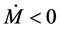
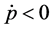
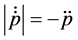
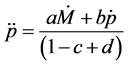
Equations (5.1) and (5.2) shows that the initial price asymmetry under changes in the quantity of money (Proposition 1) not only persists as time goes by, it also increase its magnitude when the quantity of money deviates from its equilibrium value. Propositions 1 and 2 are resumed in figure 1.
3. Discussion of propositions 1 & 2
This subsection discusses briefly previous results. The logical economic mechanisms operating behind the price asymmetry are 1) the neutral money axiom; 2) the liquidity preference and how does it relates to the risk averse effect. In the first case, we use this fundamental building block theory in order to work over a logical deduction that follows from the neutral money axiom as the raison of price movements. On the second case, the liquidity
Figure 1. Price dynamics under changes in the quantity of mo- ney, featuring Propositions 1 & 2.
preference and its relation with volatility simply suggest that when the volatility of prices goes up, even in inflation or deflation, risk-averse attitude implies a decrease in the demand for money, increasing the EMSF.
Altogether the result is described as follows. Money functions as a reserve of value and monetary actions have a quicker impact over prices compare with monetary contractions. This can be explained due to the com-
bination of the risk averse effect 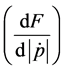
tion occurs, the increase in the value of 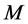
4. Conclusion
This theoretical result resembles what Brandt and Wang [6] show empirically: the volatility of inflation is time-varying and tends to be high when the level of inflation is high; therefore, deflation periods will possess a lower volatility level compared to those characterized by high inflation. Since the mechanical process underling price reactions are quite different in the upward adjustment case 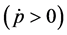
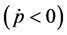
Acknowledgements
We thank Universidad de Palermo, Facultad de Ciencias Economicas for available funding. Pablo Schiaffino wishes to thank J. H.G Olivera. Much of the spirit of this note is based on the conversations that the two academics hold over this particularly issue between 2011 and 2013.
References
- Meyer, J. and Cramon-Taubadel, S. (2004) Asymmetric Price Transmission: A Survey. Journal of Agricultural Economics, 55, 581-611. http://dx.doi.org/10.1111/j.1477-9552.2004.tb00116.x
- Maskin, E. and Tirole, J. (1988) A Theory of Dynamic Oligopoly, II: Price Competition, Kinked Demand Curves, and Edgeworth Cycles. Econometrica: Journal of the Econometric Society, 56, 571-599. http://dx.doi.org/10.2307/1911701
- Sen, D. (2004) The Kinked Demand Curve Revisited. Economics Letters, 84, 99-105. http://dx.doi.org/10.1016/j.econlet.2004.01.005
- Schiaffino, P. (2010) A Theory of Kinked Demand Curve: Dynamic Game Theory and Price Rigidity. Anales de la Asociación Argentina de Economía Política. http://www.aaep.org.ar/anales/works/works2010/schiaffino.pdf
- Olivera, J.H. (1984) Note sur l’inflexibilité des prix á la baisse. Revue d’économie politique, 94, 808-810.
- Brandt, M.W. and Wang, K.Q. (2003) Time-Varying Risk Aversion and Unexpected Inflation. Journal of Monetary Economics, 50, 1457-1498. http://dx.doi.org/10.1016/j.econlet.2004.01.005