Theoretical Economics Letters
Vol.3 No.3(2013), Article ID:32954,3 pages DOI:10.4236/tel.2013.33031
A Bias in Jensen’s Alpha When Returns Are Serially Correlated
College of Business, Korea Advanced Institute of Science and Technology, Seoul, South Korea
Email: jkkang@business.kaist.ac.kr, soonhee@business.kaist.ac.kr
Copyright © 2013 Jangkoo Kang, Soonhee Lee. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 31, 2013; revised April 30, 2013; accepted May 31, 2013
Keywords: Performance Measurement; Jensen’s Alpha; Time-Varying Risk
ABSTRACT
This paper shows that Jensen’s alpha may be a biased performance measure even for public-information-based portfolios, unless the benchmark portfolio return has no serial correlation, and the bias can be substantial even when the underlying asset pricing model holds.
1. Introduction
A good performance measure should do two things. First, it should assign zero to passive portfolios or public-information-based portfolios. Second, it should assign positive numbers to good performers and negative numbers to bad performers.
Jensen’s alpha, proposed by Jensen (see [1]), is the most popular portfolio performance measure in finance. However, it is known that Jensen’s alpha is not a suitable performance measure for market timers. It sometimes assigns negative numbers to successful market timers (e.g., see [2]), violating the second condition for a good performance measure.
This paper shows that it does not satisfy the first condition, either. It has been generally believed that Jensen’s alpha assigns zero to passive portfolios or random unsuccessful market timers. It is true only when market returns are serially independent. When market returns are serially correlated, Jensen’s alpha can be a biased performance measure even for public-information-based portfolios. We provide an explicit formula to evaluate the bias in this case.
This paper shows that we need to be more careful when we interpret the results of the performance evaluation.
2. A Bias in Jensen’s Alpha
We make the following assumptions in this paper:
1) For every individual asset i, its return, ri satisfies,
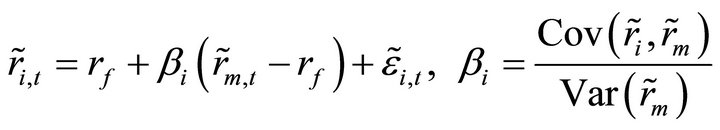 (1)
(1)
where 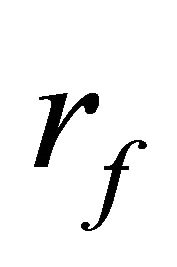 is a constant,
is a constant,  is normally distributed with mean,
is normally distributed with mean, 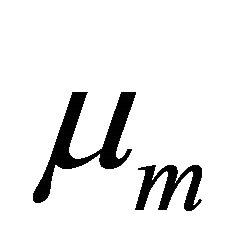 , and standard deviation,
, and standard deviation, 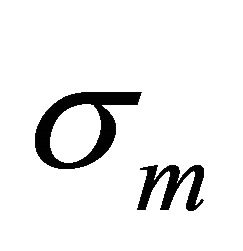 , and
, and 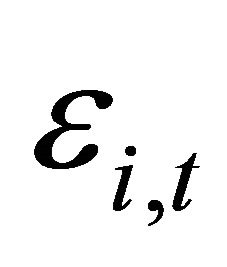 is independent of
is independent of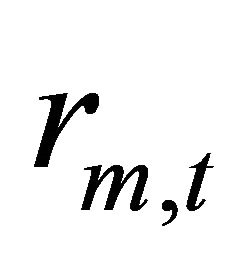 . In the CAPM,
. In the CAPM,  can be interpreted as the time t return on the market portfolio.
can be interpreted as the time t return on the market portfolio.
2) 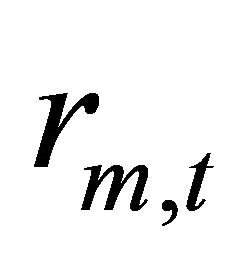 is serially correlated. That is,
is serially correlated. That is,
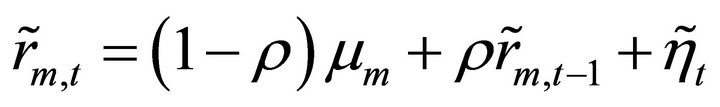 (2)
(2)
where 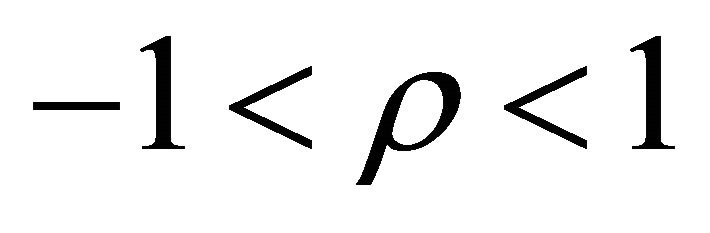 and ht is i.i.d, is independent of rm,t and follows the normal distribution with mean 0 and variance
and ht is i.i.d, is independent of rm,t and follows the normal distribution with mean 0 and variance  .
.
Under the assumptions above, Jensen’s alpha may be regarded as a reasonable performance measure on a portfolio. That is, the performance of a portfolio can be measured as:
 (3)
(3)
Now, think of the following portfolio strategy, P: Hold the market portfolio when 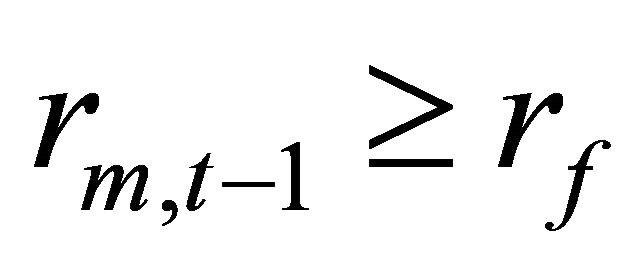 and hold a riskfree asset when
and hold a riskfree asset when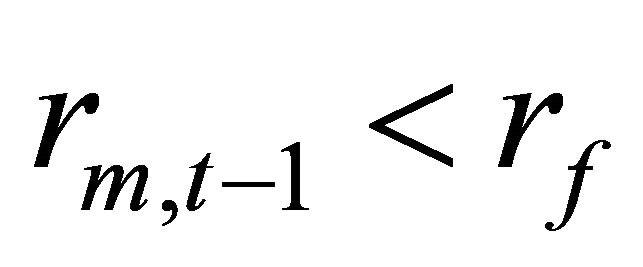 . Then, the time t return on P is:
. Then, the time t return on P is:
 (4)
(4)
Portfolio P is a public-information-based portfolio, since its time t strategy is only based on the information set at time t − 1. If Jensen’s alpha is a good performance measure, it should assign 0 to this portfolio.
Lemma: Suppose X follows the standard normal distribution. Then,
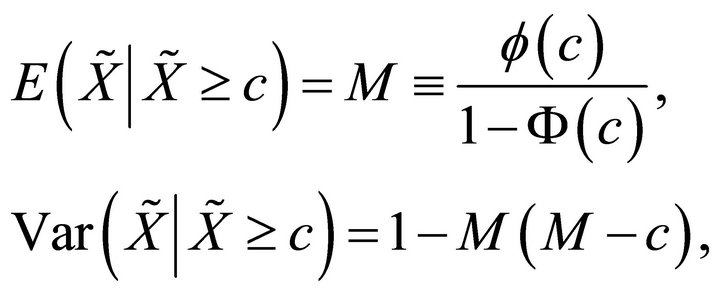 (5)
(5)
where ![]() and
and 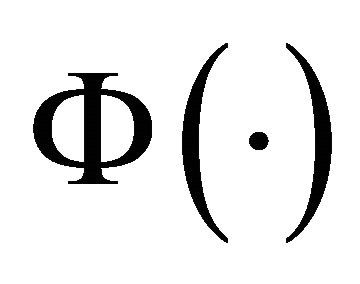 denote the standard normal probability density function and standard normal distribution function, respectively (proof: See p. 365 in [3].)
denote the standard normal probability density function and standard normal distribution function, respectively (proof: See p. 365 in [3].)
Theorem: Jensen’s alpha for the portfolio strategy P is:

where .
.
(proof) From the lemma, if we let 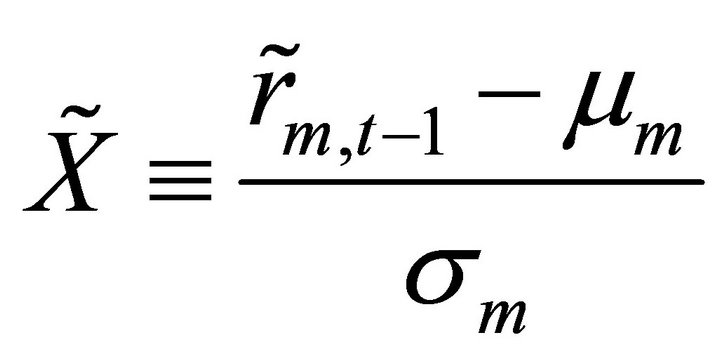
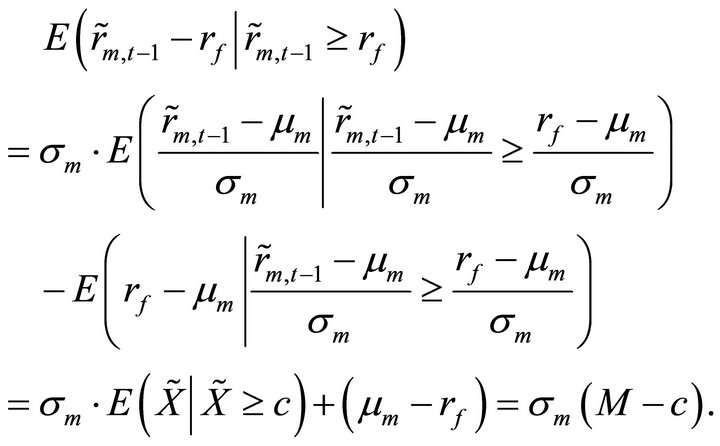 (6)
(6)
In addition,
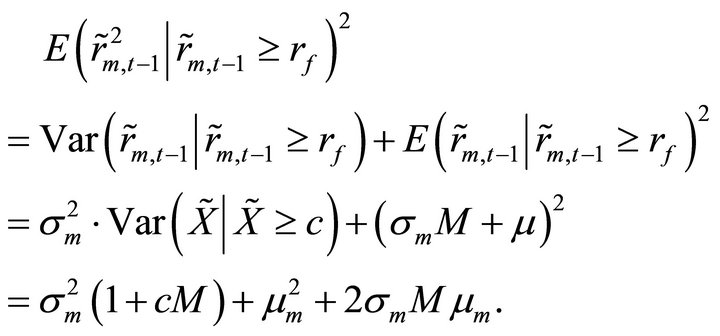 (7)
(7)
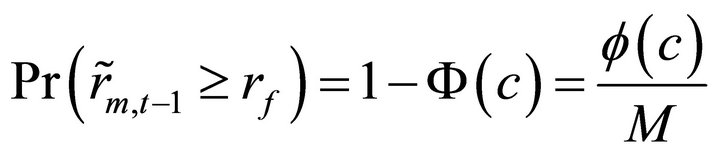 (8)
(8)
Hence,
 (9)
(9)
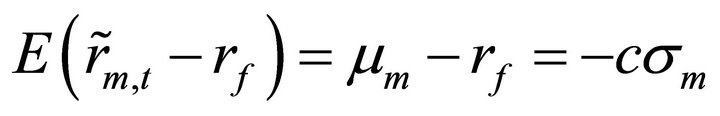 (10)
(10)
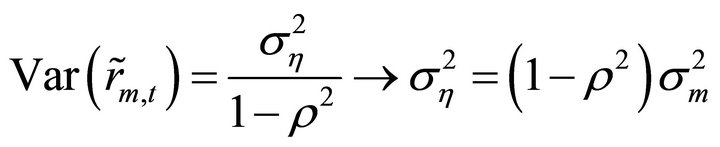 (11)
(11)
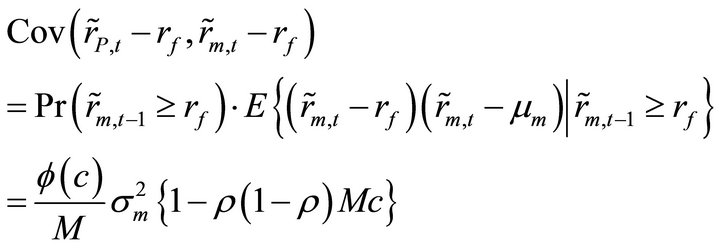 .(12)
.(12)
Therefore,
 (13)
(13)
 (14)
(14)
(end of proof)
The theorem shows that Jensen’s alpha is a biased performance measure even for some public-informationbased portfolios, unless the market return has no serial correlation , even when the underlying asset pricing model holds (as in the first assumption in this section). Extending the theorem, we can say that Jensen’s alpha may be a biased performance measure if the market return is predictable.
, even when the underlying asset pricing model holds (as in the first assumption in this section). Extending the theorem, we can say that Jensen’s alpha may be a biased performance measure if the market return is predictable.
The bias can be substantial in practice. Table 1 reports the bias when the CRSP value weighted portfolio or some bond portfolios are used as a benchmark portfolio. Bond portfolio returns are calculated using the CRSP Fama returns file. If a fund employs a portfolio strategy suggested in Section 2 during the period from January 1952 to December 2011, the bias can be 0.7% - 1.7%, which is substantial.
3. Conclusion
This paper shows that Jensen’s alpha may have a statistical size problem as well as a power problem known in the literature, if the benchmark return is serially correlated or predictable. The formula for the bias in this case is provided in the paper and the bias can be as large as 1.7% for the stock portfolio case and 1.0% for the bond portfolio case. This suggests that the conditional version of the CAPM such as Ferson and Schadt ([4]), Kang, et
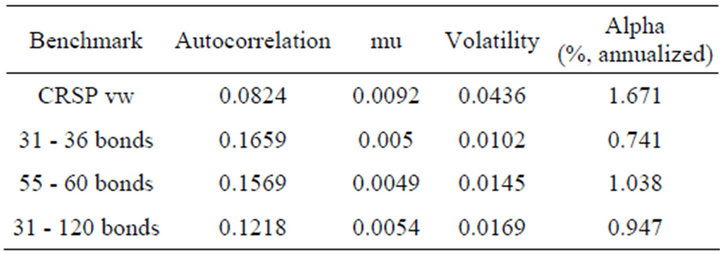
Table 1. A bias of Jensen’s alpha for the switching portfolio strategy.
al. ([5]) and Lettau and Ludvigson ([6]) should be used rather than the unconditional Jensen measure even when the CAPM holds.
REFERENCES
- M. C. Jensen, “The Performance of Mutual Funds in the Period 1945-1964,” Journal of Finance, Vol. 23, No. 2, 1968, pp. 389-416. doi:10.1111/j.1540-6261.1968.tb00815.x
- M. Grinblatt and S. Titman, “Portfolio Performance Evaluation: Old Issues and New Insights,” Review of Financial Studies, Vol. 2, No. 3, 1989, pp. 393-421. doi:10.1093/rfs/2.3.393
- G. S. Maddala, “Limited-Dependent and Qualitative Variables in Econometrics,” Econometric Society Monographs, Cambridge University Press, Cambridge, 1983.
- W. Ferson and R. Schadt, “Measuring Fund Strategy and Performance in Changing Economic Conditions,” Journal of Finance, Vol. 51, No. 2, 1966, pp. 425-461. doi:10.1111/j.1540-6261.1996.tb02690.x
- J. Kang, T. S. Kim, C. Lee and B. Min, “Macroeconomic Risk and the Cross-Section of Stock Returns,” Journal of Banking and Finance, Vol. 35, No. 12, 2011, pp. 3158- 3173. doi:10.1016/j.jbankfin.2011.04.012
- M. Lettau and S. C. Ludvigson, “Resurrecting the (C)CAPM: A Cross-Sectional Test When Risk Premia Are TimeVarying,” Journal of Political Economy, Vol. 109, No. 6, 2001, pp. 1238-1287. doi:10.1086/323282

