Theoretical Economics Letters
Vol.3 No.1(2013), Article ID:28170,9 pages DOI:10.4236/tel.2013.31011
Which Spouse First Decides in the Household? The Dynamics of Bargaining
1Departamento de Análisis Económico, Facultad de Economía y Empresa, Universidad de Zaragoza, Zaragoza, Spain
2Institute for the Study of Labour-IZA, Bonn, Germany
Email: jandaluz@unizar.es, mmarcen@unizar.es, jamolina@unizar.es
Received December 14, 2012; revised January 15, 2013; accepted February 16, 2013
Keywords: Family Bargaining; Stackelberg Game; Family Good
ABSTRACT
This paper examines the effects of which spouse first decides in the intrahousehold decision on the time that each spouse devotes to the provision of a family good. Specifically, we adopt a dynamic approach by developing a supergame, with the status quo being sequential, to study the influence of the discount factor, which measures the importance of the future, on the set of sustainable agreements in intrahousehold bargaining. We first show that cooperation is easily sustained. We then observe a positive relationship between the discount factor and the proportion of time that the follower devotes to housework, when focusing on sustainable agreements, with this finding being maintained even if the follower has higher wages than the spouse leader.
1. Introduction
Although the comparative advantage of women in household production may have explained specialization in the past, Becker [1], this traditional theory is unable to explain the current empirical evidence on the contribution to housework. Despite the increase in female labor force participation and female human capital, specialization within the household has remained relatively unchanged, Aguiar and Hurst [2]. Many women choose working arrangements that are compatible with caring for their children. Hersch [3], and indeed, women who work more hours than their husbands outside the home, or those who have higher earnings than their husbands do relatively more housework, Akerlof and Kranton [4].
Bargaining theories also fail to predict these findings. Under this approach, it would be expected a more egalitarian allocation of time within the household as female human capital increases. Even more recent works on bargaining models of family decision-making, which extend the one-period approach to a dynamic setting, predict a reduction in the incentives to specialize in household production, Lundberg and Pollak [5]. In this setting, a consumption-smoothing problem arises, which may lead to the inability of spouses to engage in inter-temporal agreements, and that could lead to an inefficient allocation of household resources. The problem here is that a credible promise to compensate family public good production with future consumption cannot be made. The sustainability of family bargaining agreements in a dynamic setting is also analyzed in Andaluz and Molina [6]. By considering the trigger strategy, Friedman [7], as a punishment scheme, they show that the spouse with the higher bargaining power has a greater incentive to reach an agreement.1 Since bargaining power is not the only relevant factor in a dynamic family decision-making process, we add to this work by analyzing the influence of the discount factor, which measures the importance of the future, on the set of sustainable agreements, and on the time that each spouse devotes to the provision of a family good.
Our paper builds on the work of Andaluz and Molina [6], with one important distinction: we extend the analysis of the dynamic aspects of the family bargaining process, developing a supergame in which the status quo is not only defined as non-cooperative, but also as sequential. We suppose that the spouses play a non-cooperative Stackelberg game, where the leader decides, first, contributions to a certain quantity of provision of family good, and thereby sets restrictions for the follower.
In our paper, we first solve the one-shot game, a Stackelberg game, and we then use this as the state game of an infinitely repeated game. To choose among the multiple equilibria of the repeated game, we focus on sustainable solutions and we determine the efficient allocation by way of the symmetric Nash bargaining solution. Using methodologies similar to ours, other studies such as Espinosa and Rhee, [8], have examined the relationship between a union and a firm by developing a supergame with a threat to return to a noncooperative Stackelberg equilibrium.
How does a spouse become a Stackelberg leader or a Stackelberg follower? In the literature of the economics of the family, we find several examples of marital relationships modeled as a Stackelberg game. Bolin [9,10] suggests that a wife may be a Stackelberg follower if she considers the decisions taken by her husband as a fait accompli. Bolin analyzes the division of family work as the outcome of a Stackelberg game, showing that not only comparative advantage but also dominance are important factors in time allocation. Another argument is proposed by Elul et al. [11], who consider that the age difference between spouses gives the husband a time advantage in the sequential decision game of time allocation, through an analysis of the gender wage gap. Beblo and Robledo [12] also study the wage gap, but jointly with the gender leisure gap, providing empirical evidence that husbands enjoy more leisure time, all other things being equal, than their wives. They explain this empirical finding as a result of the husband being the Stackelberg leader in a sequential private provision game. In our case, we could also consider a situation in which the household division of labor is affected by social norms. The prescription that women should do the work at home may alter the family decision-making process, since one spouse, normally the husband, can make a credible commitment to contribute no more than a possibly very small amount to the provision of a family good. Thus, this spouse, usually the husband, becomes a Stackelberg leader and the other spouse, the wife, becomes a Stackelberg follower.
As regards the main results, we observe an increase in the set of sustainable agreements derived from the bargaining, in a family setting, when the discount factor is higher. Thus, cooperation is more easily sustained. We also study the impact of the discount factor on the gains to well-being derived from cooperation, in order to analyze whether the leader or the follower has incentives to reach an agreement. Although, in this case, our results are ambiguous, we show that the time devoted by the leader to the production of the family good is a key element in determining the sign of the relationship between the welfare gains and the discount factor.
Focusing on the sustainable solutions, we examine the relationship between the discount factor and the time devoted to the provision of a family good. What is clearly observed is that the contribution of the follower to the family good is increasing with respect to the discount factor. Then, if the woman is the follower (for instance, she decides second because of the existence of social norms), we would expect her contribution to a family good to be greater when the discount factor increases (when women place more value on the future), even if there are no differences in the wages for men and women.2 This prediction appears to be confirmed by current empirical research that finds that wives undertake larger shares of the housework, regardless of their earnings.
2. Preferences
We suppose that the utility of each agent takes the following functional form (see Konrad and Lommerud [14]):
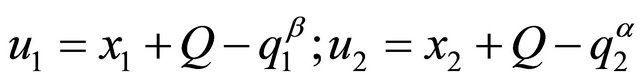 (1)
(1)
where 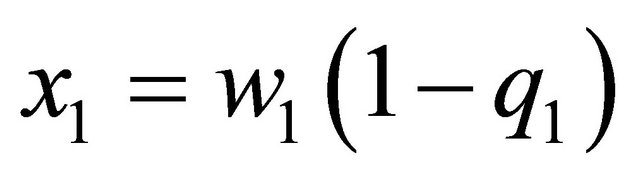 and
and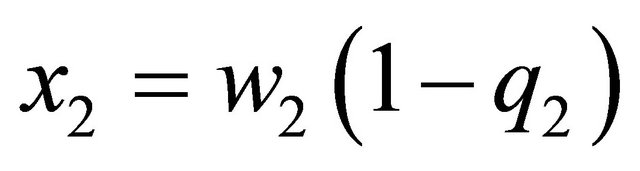 ,
,  represents the wage rate for agent
represents the wage rate for agent ,
, 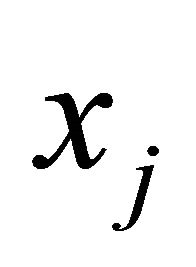 indicates the private consumption of agent
indicates the private consumption of agent ,
, 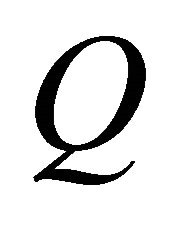
 represents the family good,
represents the family good,  with
with 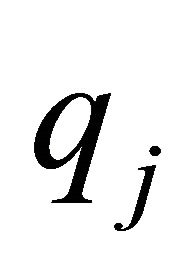 being the proportion of hours that agent
being the proportion of hours that agent  devotes to the provision of this good.
devotes to the provision of this good.
The maximum time available for each spouse is normalized to 1. In line with Konrad and Lommerud [14], we suppose that individuals increasingly dislike spending more time on the production of the family good. The contribution to the family good not only reduces the time available to the labor market, but also has a psychologycal cost, represented by an increasing and convex function in each of these arguments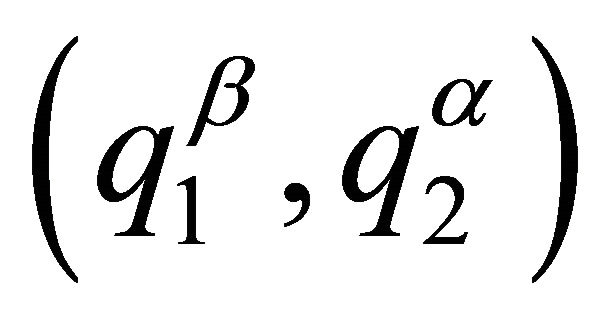 , with
, with  and
and  being greater than 1. The family good,
being greater than 1. The family good,  , can include any situation which requires the joint performance of the spouses, e.g., raising the children or the maintenance of the home, but it excludes the possibility that the provision of the family good would be obtained in the market. This assumption can be reasonable if it takes into consideration that, for some couples, the private provision of family goods is not a substitute for their own contribution to the family good. (Though it is not the aim of this paper, our model can be extended by considering both kinds of provision of family goods).
, can include any situation which requires the joint performance of the spouses, e.g., raising the children or the maintenance of the home, but it excludes the possibility that the provision of the family good would be obtained in the market. This assumption can be reasonable if it takes into consideration that, for some couples, the private provision of family goods is not a substitute for their own contribution to the family good. (Though it is not the aim of this paper, our model can be extended by considering both kinds of provision of family goods).
We choose this special functional form for simplicity, although we acknowledge that this form can be restrictive. When the spouses act non-cooperatively, the provision of the family good by both agents is strategically independent, even though their utilities are intertwined through the existence of a family good. Then, this specification establishes the non-cooperative outcome as a benchmark for understanding the family decision-making process.
3. The One-Shot Game
To analyze how the discount factor affects both the set of sustainable agreements and time that each individual devotes to the provision of a family good, we first solve the one-shot game, a Stackelberg game, and we then use this as the state game of an infinitely-repeated game, using reversion to this non-cooperative Stackelberg equilibrium as the punishment for deviators. To determine the optimum levels of consumption and the contribution to the family good among the multiple stationary paths of the repeated game, we focus on sustainable solutions and we determine the efficient allocation as a result of the symmetric Nash bargaining solution, (see De la Rica and Espinosa [15]).
In each period , the non-cooperative equilibrium is the outcome of a Stackelberg game, in which the leader (spouse 1) commits to a certain quantity of provision of family good, while anticipating the optimal contribution of the follower (spouse 2).
, the non-cooperative equilibrium is the outcome of a Stackelberg game, in which the leader (spouse 1) commits to a certain quantity of provision of family good, while anticipating the optimal contribution of the follower (spouse 2).
Applying the backward induction procedure, we begin by obtaining the equilibrium corresponding to spouse  (the follower). Formally:
(the follower). Formally:
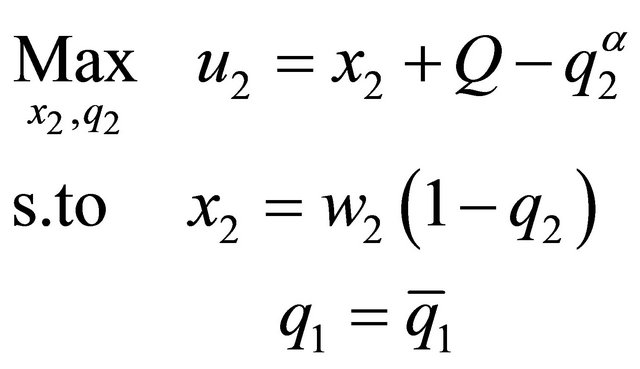 (2)
(2)
From here, we deduce the levels of consumption and the provision of the family good:
 (3)
(3)
and the utility level:
 (4)
(4)
For spouse 1 (the leader) we formulate the following maximization problem:
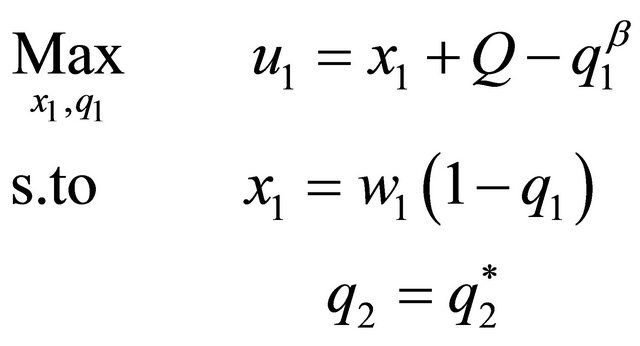 (5)
(5)
and we obtain the level of private consumption, and the provision of the household good made by spouse 1:
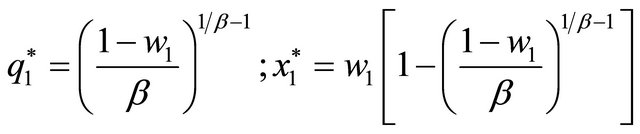 (6)
(6)
Therefore, the levels of utility in the non-cooperative solution for both spouses are:
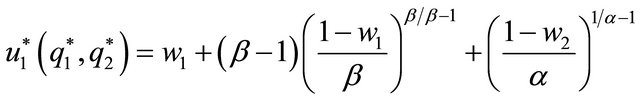 (7)
(7)
 (8)
(8)
The solution obtained in (3) and (6), is an interior solution.3 In addition, we may determine the situations in which only one of the spouses is the contributor to the family good, to see whether there is a dominant strategy (see Bucholz et al., [16]). We can distinguish two additional Stackelberg equilibria:
The leader is the only contributor.
In this case,  , the family good, is only supplied by spouse 1, from (5) and with
, the family good, is only supplied by spouse 1, from (5) and with 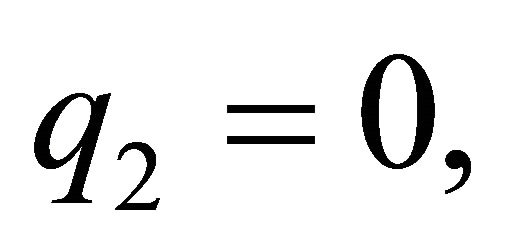 we can obtain the total family good:
we can obtain the total family good: 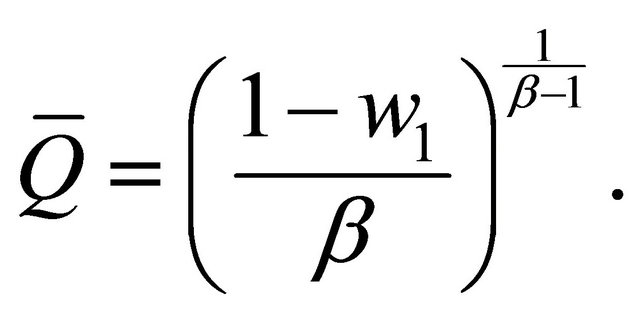 and the levels of utility of both spouses:
and the levels of utility of both spouses:
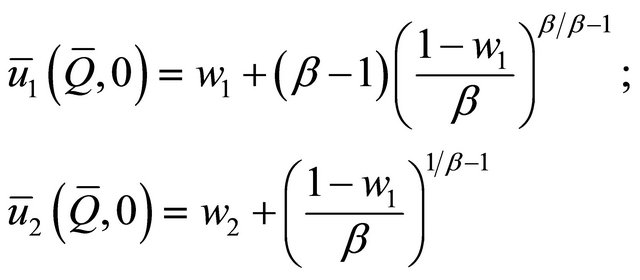
The follower is the only contributor.
From the maximization problem of spouse 2, (2), and with 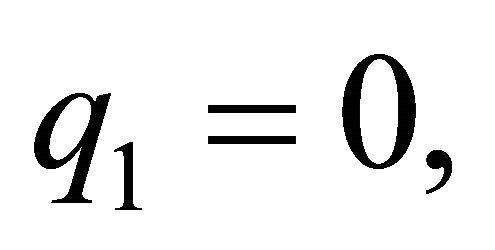 we may determine the levels of provision of family good which are only provided by spouse 2:
we may determine the levels of provision of family good which are only provided by spouse 2:
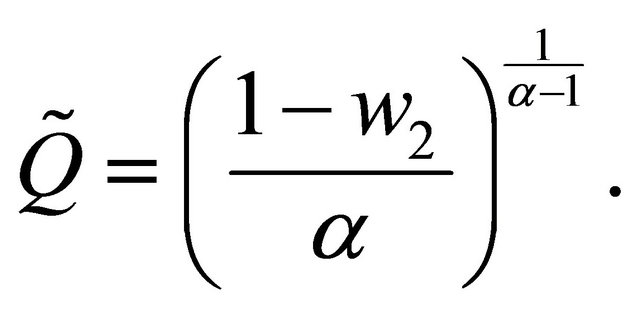
with the levels of utility for both spouses in this case being:
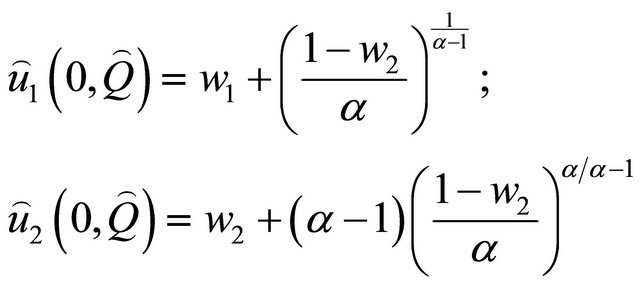
Under the structure of preferences defined above, for all values of the parameters, the interior solution constitutes a dominant strategy for both agents in the Stackelberg equilibrium.4 It is straightforward to deduce that
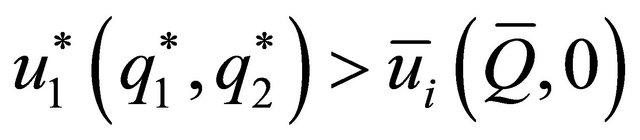
and that
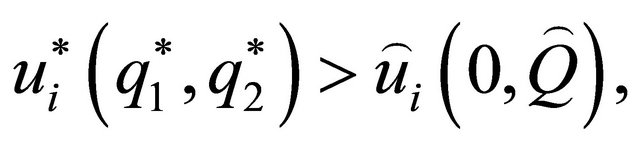
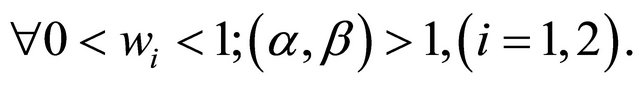 This is a reasonable result, since we do not consider the possibility that one spouse compensates the other.
This is a reasonable result, since we do not consider the possibility that one spouse compensates the other.
However, the interior solution, the dominant strategy, is clearly inefficient, as can be seen in Figure 1 where it is represented the curves of indifference of the spouses in the non-cooperative solution. For spouse , the slope of the curve of indifference in the non-cooperative equilibrium is zero in
, the slope of the curve of indifference in the non-cooperative equilibrium is zero in 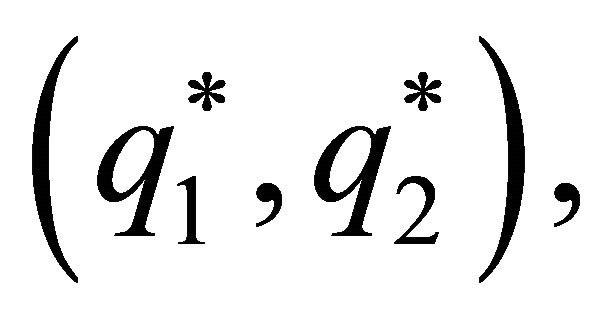 and is increasing and convex if
and is increasing and convex if 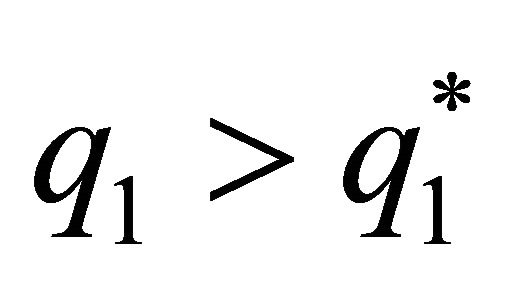 and
and
 ,
,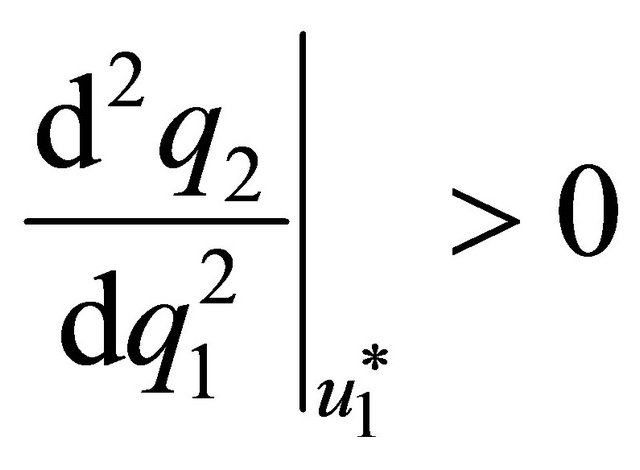 . Analogously, for spouse
. Analogously, for spouse , the slope of the curve of indifference that contains the solution of the one-shot game is equal to minus infinity in the combination
, the slope of the curve of indifference that contains the solution of the one-shot game is equal to minus infinity in the combination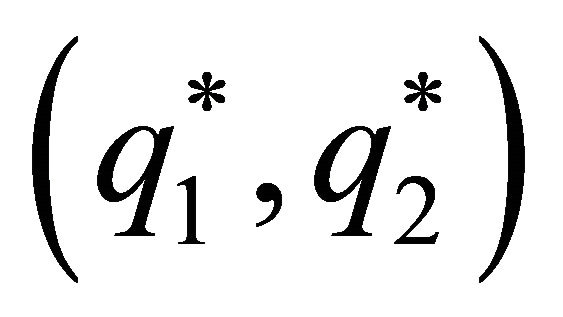 , and is increasing and concave when
, and is increasing and concave when 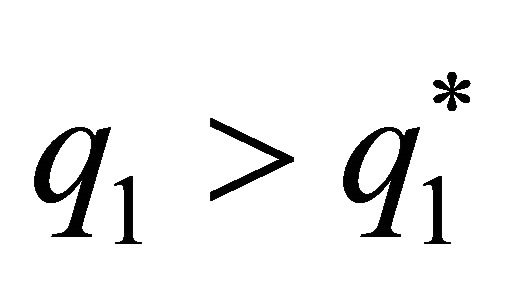 and
and 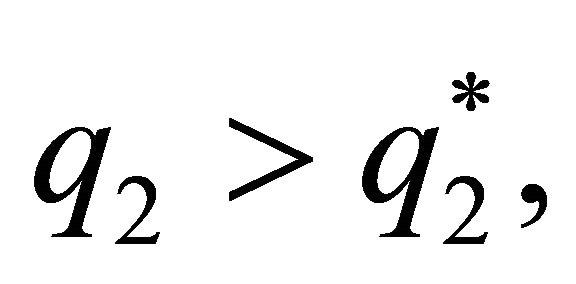
 All the points located inside the area formed by both curves of indifference are Pareto superior to the equilibrium of the one shot game, as Kapteyn and Kooreman [17] demonstrated. Those points located in the contract curve CC’ are efficient solutions.
All the points located inside the area formed by both curves of indifference are Pareto superior to the equilibrium of the one shot game, as Kapteyn and Kooreman [17] demonstrated. Those points located in the contract curve CC’ are efficient solutions.
4. Dynamic Setting
We consider an infinitely-repeated game, in which the two members of a family, spouse 1 and spouse 2, may contribute voluntarily to the provision of a family good whose consumption is non-rival, as in [3]. We suppose that the spouses do not know the moment of the dissolution of the marriage, and that the objective of each is to

Figure 1. Set of Pareto-Superior Solutions.
maximize the discounted value of their current utilities.5 Formally:
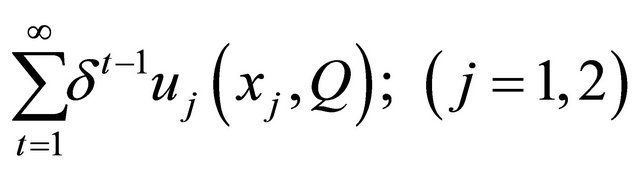
where  denotes the discount factor, common to both agents.
denotes the discount factor, common to both agents.
Is it possible to reach an efficient equilibrium in a dynamic setting? When the decisions are taken in a multi-period framework, the loss from non-cooperation accumulates, and strong incentives appear to reach a Pareto Superior agreement. However, repetition alone is not enough to eliminate the non-cooperative static equilibrium, and thus the one-shot Stackelberg equilibrium is another possible outcome of the repeated game. To arrive at a combination that is Pareto superior to the one-shot non-cooperative equilibrium, it is necessary that both spouses implicitly create a credible strategy that deters deviations from a cooperative solution. As in Andaluz and Molina [6], we consider the so-called trigger strategy (Friedman [7]). In this case, when there is a deviation from the cooperative solution, the levels of private consumption, and the provision of the family good revert to those of non-cooperative equilibrium. The threat of retaliation, through reversion to this punishment path, sustains Pareto Superior outcomes and is credible, since it is in the best interest of each agent not to deviate unilaterally from the cooperative equilibrium.
For the sake of simplicity, we focus on stationary paths for all . In a subgame perfect equilibrium, a stationary path is sustainable if it satisfies the following conditions:
. In a subgame perfect equilibrium, a stationary path is sustainable if it satisfies the following conditions:
 (9)
(9)
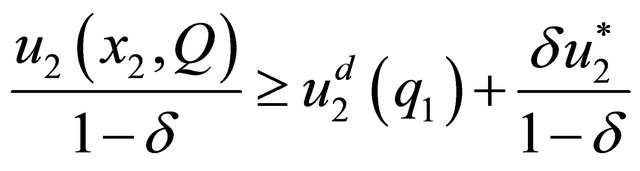 (10)
(10)
Condition (9) establishes that both spouses have incentives to cooperate, since the well-being these agents obtain in the cooperative solution is greater than, or equal to, the well-being obtained in the non-cooperative solution. Condition (10) determines that the spouse who decides second has no incentive to deviate from the efficient solution. Condition (9) is not enough to obtain stationary paths, since the follower, given  could react by deviation to maximize his/her own utility. To solve this problem, it is necessary to introduce inequality (10), which states that the discounted value of the well-being of the follower, conforming to the specified path, the left-hand side of the inequality, is greater than the well-being from the optimal one-shot deviation and the subsequent reversion from the following period, onwards to the punishment path, the right-hand side of the inequality.6
could react by deviation to maximize his/her own utility. To solve this problem, it is necessary to introduce inequality (10), which states that the discounted value of the well-being of the follower, conforming to the specified path, the left-hand side of the inequality, is greater than the well-being from the optimal one-shot deviation and the subsequent reversion from the following period, onwards to the punishment path, the right-hand side of the inequality.6
In this setting, the maintenance of the cooperative equilibrium depends on the agent who decides second. If spouse  deviates from a cooperative agreement, this is immediately observed by spouse
deviates from a cooperative agreement, this is immediately observed by spouse , thus eliminating any possible short-term well-being gains for spouse
, thus eliminating any possible short-term well-being gains for spouse . Moreover, the leader’s discount rate plays no role, since the one-shot game is sequential. However, the follower’s discount rate is a key element in the maintenance of the cooperative solution.
. Moreover, the leader’s discount rate plays no role, since the one-shot game is sequential. However, the follower’s discount rate is a key element in the maintenance of the cooperative solution.
Unless  is very high, constraint (10) is always binding in equilibrium, whereas (9) is not. Denote
is very high, constraint (10) is always binding in equilibrium, whereas (9) is not. Denote  the minimum value of discount factor for which (10) is not binding, and let the function
the minimum value of discount factor for which (10) is not binding, and let the function 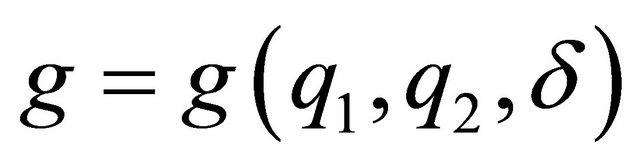 represent the long-term gain from the follower’s cooperation determined from (10). Formally:
represent the long-term gain from the follower’s cooperation determined from (10). Formally:
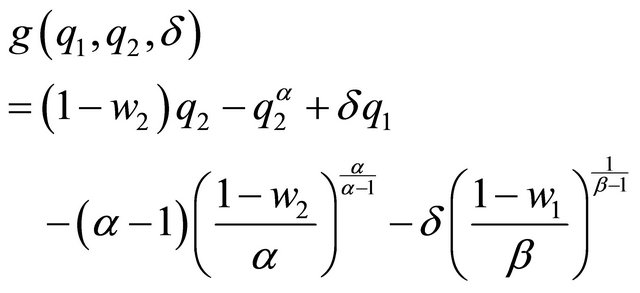 (11)
(11)
When 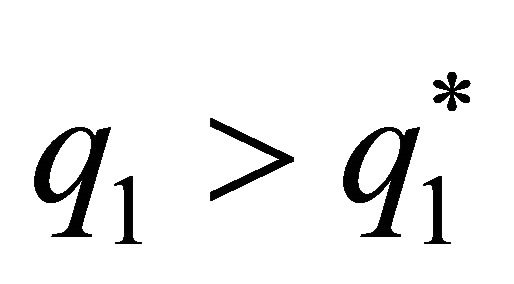 and
and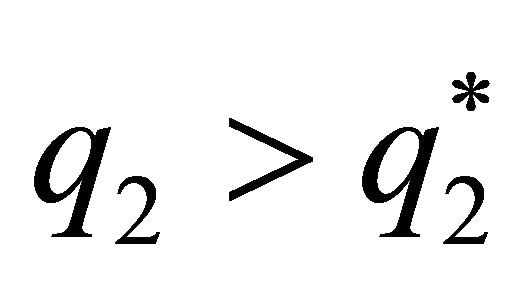 , the function
, the function 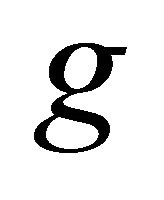 is increasing and concave, with the value of its slope being minus infinity in the non-cooperative solution
is increasing and concave, with the value of its slope being minus infinity in the non-cooperative solution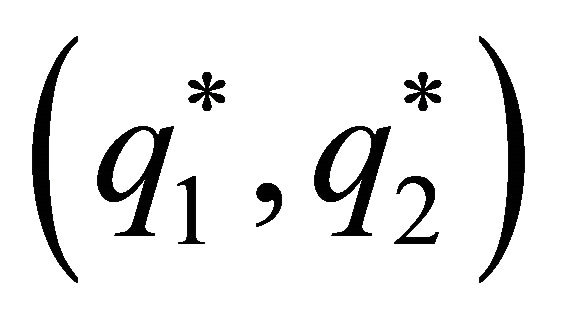 . The function
. The function 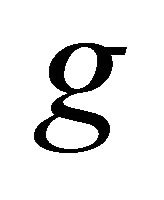 is represented by a broken line in Figure 1. Among the Pareto-superior combinations
is represented by a broken line in Figure 1. Among the Pareto-superior combinations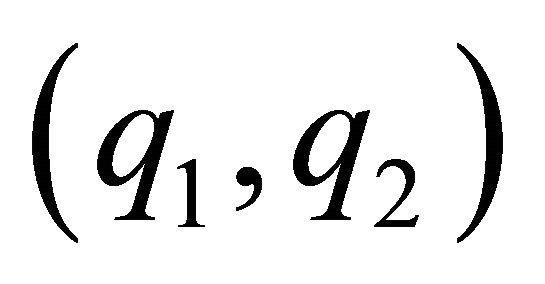 , which are those points located in the contract curve CC’, the function
, which are those points located in the contract curve CC’, the function  allows us to identify a subset of sustainable solutions, all the combinations of
allows us to identify a subset of sustainable solutions, all the combinations of 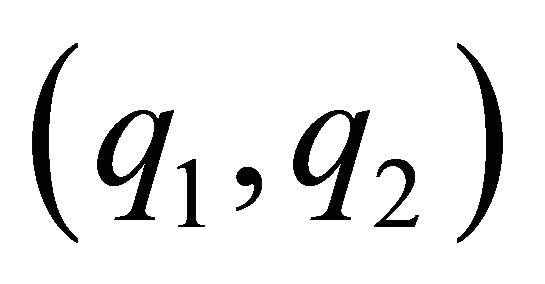 located to the right of the dashed line, which can be achieved by way of repeated interaction. This subset of Pareto-superior solutions to the equilibrium of the oneshot game is greater when the discount factor is higher, since the function
located to the right of the dashed line, which can be achieved by way of repeated interaction. This subset of Pareto-superior solutions to the equilibrium of the oneshot game is greater when the discount factor is higher, since the function 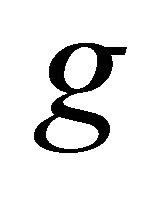 is increasing in
is increasing in  Thus, cooperation is more easily sustained as
Thus, cooperation is more easily sustained as  increases.
increases.
5. Bargaining Solution
In order to determine a single equilibrium among the multiple stationary paths, we suppose that there exists a bargaining process, not modeled explicitly here, and as a result, both spouses take their decisions by way of the symmetric Nash bargaining solution.7 Focusing on the sustainable solutions, spouses choose the stationary paths of private consumption and family good provision that maximize the product of the utilities, after being normalized by the utility levels of the non-cooperative solution. Formally, the problem becomes, for 
 (12)
(12)
When  takes value zero, the non-cooperative solution satisfies restrictions (9) and (10). Alternatively, if this factor takes value one, all the Pareto-superior solutions are indeed sustainable and, consequently, the bargaining agreement constitutes an efficient solution. Between these two extremes, the solution of the previous problem depends on the discount factor through constraint
takes value zero, the non-cooperative solution satisfies restrictions (9) and (10). Alternatively, if this factor takes value one, all the Pareto-superior solutions are indeed sustainable and, consequently, the bargaining agreement constitutes an efficient solution. Between these two extremes, the solution of the previous problem depends on the discount factor through constraint . The bargaining solution is determined by way of the tangency between an Iso-J line and an Iso-g line, as shown in Figure 2.8
. The bargaining solution is determined by way of the tangency between an Iso-J line and an Iso-g line, as shown in Figure 2.8
Under some regularity assumptions (see Appendix) we obtain the following proposition:
Proposition 1.
For 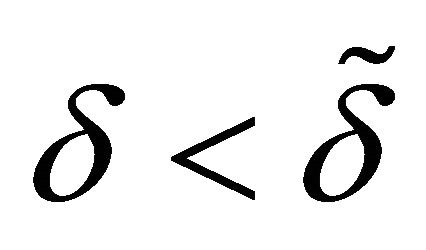
The contribution to the family good of the spouse who decides second (follower) is increasing with respect to the discount factor: 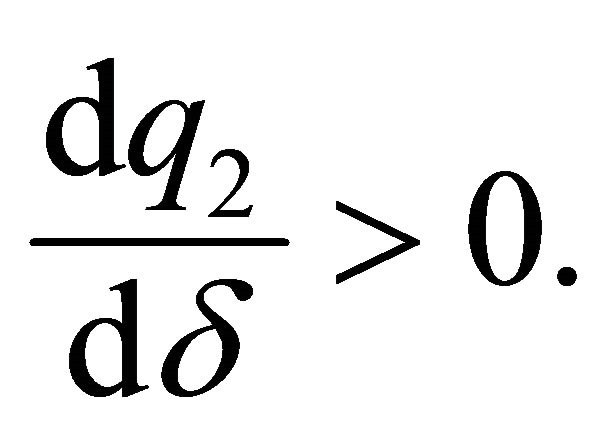
The influence of the discount factor on the contribution to the family good of the spouse who decides first
(leader) is ambiguous: 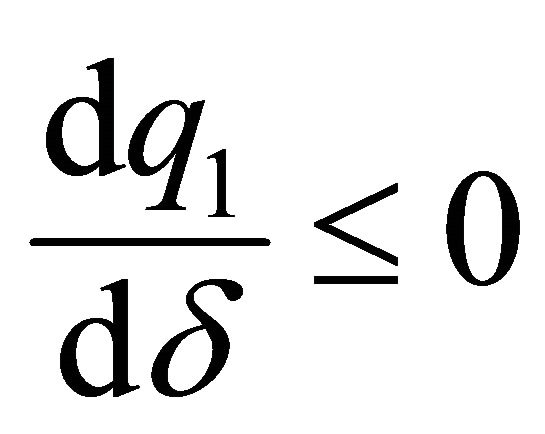 or
or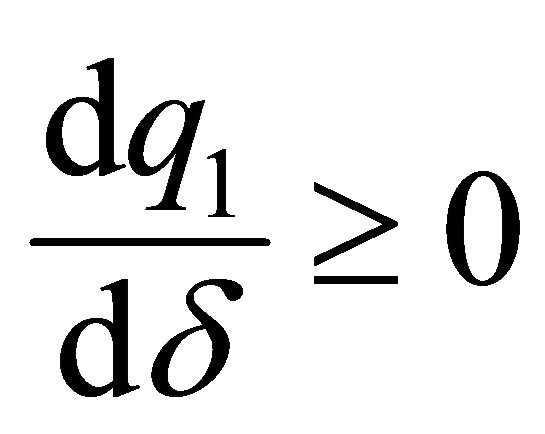 .
.
Proof. (See Appendix).
This proposition indicates that the agent who decides second will devote more time to the provision of the family good when he/she values the future heavily (a
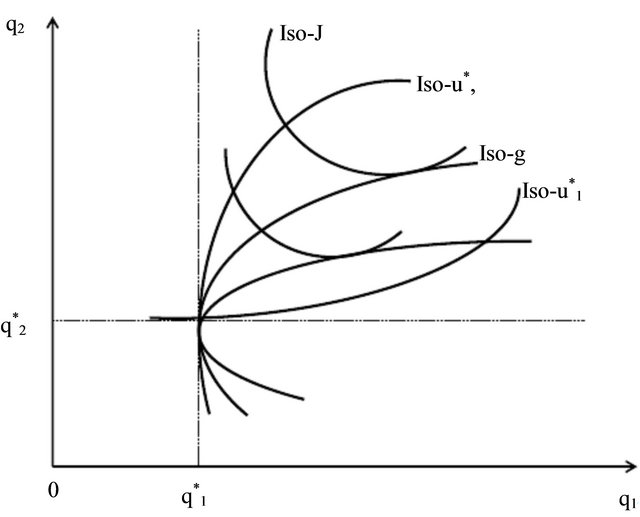
Figure 2. Set of possible sustainable bargaining solutions.
high discount factor). However, the path of the contribution to the family good made by the spouse who decides first can be increased or decreased. An increasing evolution would imply that the difference between the hours this agent devotes to the family good in the cooperative solution, and the hours determined in the noncooperative equilibrium, will not be significant.
Note that we have found that the discount factor can increase the provision of the family good without imposing any restriction on the follower’s relative earnings, or on the psychological cost produced by devoting time to the family good. Thus, if the woman is the follower, the higher the discount factor, the higher the provision of the family good, even with the wage rate being the same for both spouses.
For the leader, spouse 1, we find a subset of sustainable solutions where the spouse who decides first increases or decreases provision of the family good, depending on the discount factor. There exists a level of provision of the family good, 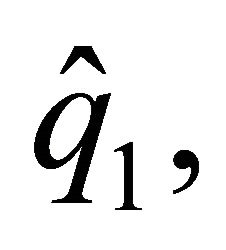 with
with 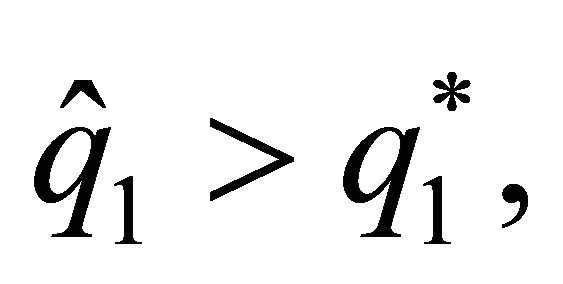 which represents the minimum value from which the relationship between the discount factor and the level of provision of the family good made by this agent becomes negative. By contrast, for
which represents the minimum value from which the relationship between the discount factor and the level of provision of the family good made by this agent becomes negative. By contrast, for  when the discount factor increases, the provision of the family good by the leader increases. Thus, situations in which the husband devotes much less time to the family good than does the wife can be possible sustainable agreements, even without differences in the salaries of the spouses, as a result of a high discount factor.
when the discount factor increases, the provision of the family good by the leader increases. Thus, situations in which the husband devotes much less time to the family good than does the wife can be possible sustainable agreements, even without differences in the salaries of the spouses, as a result of a high discount factor.
The discount factor also reflects the subjective probability that the game will end. The higher the discount factor, the lower the probability that the game will end in the near future. Even when there is a possibility that the game will end sometime in the future, as in the case of intertemporal agreements within the family subject to renegotiation, our optimum provision of the family good can support a near-efficient outcome, as long as each spouse believes, with a high enough probability, that the game will continue. Thus, although we have considered an infinitely repeated game, it is possible to make agreements in a dynamic setting with a finite horizon (see Espinosa and Rhee [8]).
Knowing the evolution of the paths of the provision of the family good, we can deduce the influence of the discount factor on the level of utility derived from the cooperation.
Corollary:
For 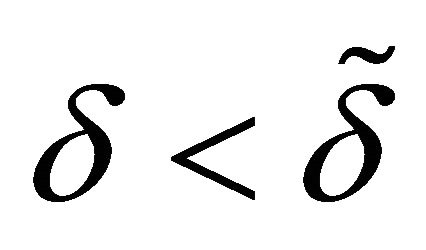
In the bargaining solution, a variation of the discount factor can increase or reduce the levels of utility for both spouses: 
Proof. (See Appendix).
Specifically, we observe that, for 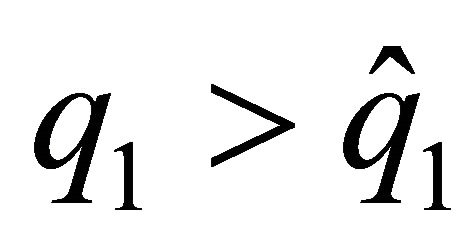 when the discount factor increases, the provision of the family good by the leader decreases, generating opposite effects on the level of utility of the spouses. The level of utility increases for the leader and decreases for the follower. By contrast, for
when the discount factor increases, the provision of the family good by the leader decreases, generating opposite effects on the level of utility of the spouses. The level of utility increases for the leader and decreases for the follower. By contrast, for 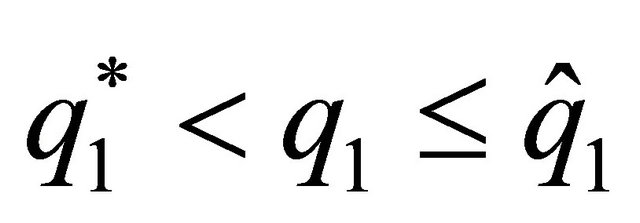 when the discount factor increases, the provision of the family good by the leader increases, and the levels of utility can increase or decrease for both spouses.
when the discount factor increases, the provision of the family good by the leader increases, and the levels of utility can increase or decrease for both spouses.
6. Conclusions
Family bargaining models have usually presented the household allocation problem in a static setting. However, households endure for more than a single period, which can potentially, and substantially, affect the family decision-making process and it is thus necessary to view bargaining in a multi-period context.
In this dynamic setting, we have set up a supergame in an intrahousehold framework, in which both spouses may contribute voluntarily to the provision of a family good. Assuming that the status quo is not only defined as non-cooperative, but also as sequential (equilibrium of Stackelberg), and that the efficient allocation is given by way of the symmetric Nash bargaining solution, we deduce the influence of the discount factor on the sustainability of agreements, and on the time that each individual devotes to the provision of the family good. We acknowledge that we have not included all the factors that affect the dynamics of intrahousehold bargaining, and some of our assumptions are potentially restrictive, but we view this work as a benchmark for understanding long-term marital relationships.
The following conclusions are obtained. First, the set of possible sustainable agreements derived from bargaining is greater when the discount factor of the spouse who decides second is higher; cooperation is more easily sustained. However, it is not clear whether a greater discount factor increases the incentives to make an agreement, since we show that the discount factor has an ambiguous impact on the gains of well-being derived from the bargaining. The effect of the discount factor will be positive or negative, depending on the increase in the time devoted by the leader to the production of the family good in the bargaining solution.
Second, the contribution of the follower to the family good is increasing with respect to the discount factor, whereas the relationship between the discount factor and the contribution made by the leader is ambiguous. Then, we would expect a greater contribution of the follower to the family good than that predicted in a static context. If the woman is the follower, it is likely that she will devote more time to a family good as her discount factor increases, despite the absence of differences in the wages for both spouses.
7. Acknowledgements
Support from the Spanish Ministry of Economics is gratefully acknowledged (grant reference number ECO2012- 34828).
REFERENCES
- G. S. Becker, “A Treatise on the Family,” Enlarged Edition, Harvard University Press, Cambridge, 1991.
- M. Aguiar and E. Hurst, “Measuring Trends in Leisure: The Allocation of Time over Five Decades,” The Quarterly Journal of Economics, Vol. 122, No. 3, 2007, pp. 969-1006. doi:10.1162/qjec.122.3.969
- J. Hersch, “The Impact of Nonmarket Work on Market Wages,” American Economic Review Papers and Proceedings, Vol. 81, 1991, pp. 157-160.
- G. Akerlof and R. Kranton, “Economics and Identity,” Quarterly Journal of Economics, Vol. 115, No. 3, 2000, pp. 715-753.
- S. Lundberg and R. A. Pollak, “Efficiency in Marriage,” Review of Economic of the Household, Vol. 1, No. 3, 2003, pp. 153-167. doi:10.1023/A:1025041316091
- J. Andaluz and J. A. Molina, “On the Sustainability of Bargaining Solutions in Family Decision Models,” Review of Economics of the Household, Vol. 5, No. 4, 2007, pp. 405-418.
- J. Friedman, “A Non-Cooperative Equilibrium for Supergames,” Review of Economic Studies, Vol. 38, No. 113, 1971, pp. 1-12.
- M. P. Espinosa and C. Rhee, “Efficient Wage Bargaining as a Repeated Game,” Quarterly Journal of Economics, Vol. 104, No. 3, 1989, pp. 565-588.
- K. Bolin, “An Economic Analysis of Marriage and Divorce,” Lund Economic Studies, University of Lund, Lund, 1996, p. 62.
- K. Bolin, “A Family with One Dominating Spouse,” In: I. Persson and C. Jonung, Eds., Economics of the Family and Family Policies, Routledge, New York, 1997, pp. 84-99. doi:10.4324/9780203441336.ch4
- R. Elul, J. Silva-Reus and O. Volij, “Will You Marry Me? A Perspective on the Gender Gap,” Journal of Economic Behaviour and Organization, Vol. 49, No. 4, 2002, pp. 549-572. doi:10.1016/S0167-2681(02)00006-9
- M. Beblo and J. R. Robledo, “The Wage Gap and the Leisure Gap for Double-Earner Couples,” Journal of Population Economics, Vol. 21, No. 2, 2008, pp. 281- 304.
- D. J. Benjamin, J. J. Choi and A. J. Strickland, “Social Identity and Preferences,” American Economic Review, Vol. 100, No. 4, 2010, pp. 1913-1928.
- K. A. Konrad and K. E. Lommerud, “The Bargaining Family Revisited,” Canadian Journal of Economics, Vol. 33, No. 2, 2000, pp. 471-487.
- S. De la Rica and M. P. Espinosa, “Testing Employement Determination in Unionised Economies as a Repeated Game,” Scottish Journal of Political Economy, Vol. 44, No. 2, 1997, pp. 134-152.
- W. Buchholz, K. A. Konrad and K. E. Lommerud, “Stackelberg Leadership and Transfers in Private Provision of Public Goods,” Review of Economic Design, Vol. 3, No. 1, 1997, pp. 29-43.
- A. Kapteyn and P. Kooreman, “On the Empirical Implementation of Some Game Theoretic Models of Household Labor Supply,” The Journal of Human Resources, Vol. 25, No. 4, 1990, pp. 584-598.
- K. Binmore, A. Rubinstein and A. Woolinsky, “The Nash Bargaining Solution in Economic Modeling,” Rand Journal of Economics, Vol. 17, No. 2, 1986, pp. 176-188.
- J. C. Harsanyi, “Rational Behaviour and Bargaining Equilibria in Games and Social Situations,” Cambridge University Press, Cambridge, 1977. doi:10.1017/CBO9780511571756
Appendix
Proof of Proposition To be able to characterize the solution of the maximization problem proposed in (12), we introduce the following assumptions:
We suppose that 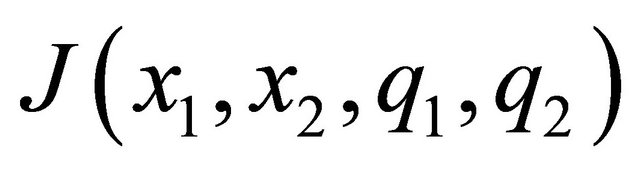 is strictly concave.
is strictly concave.
The level curves of 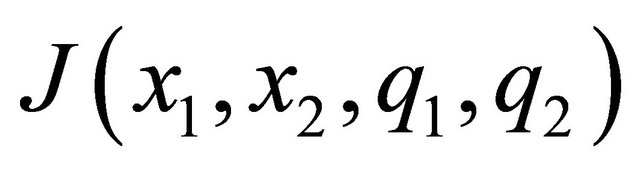 are monotone:
are monotone:
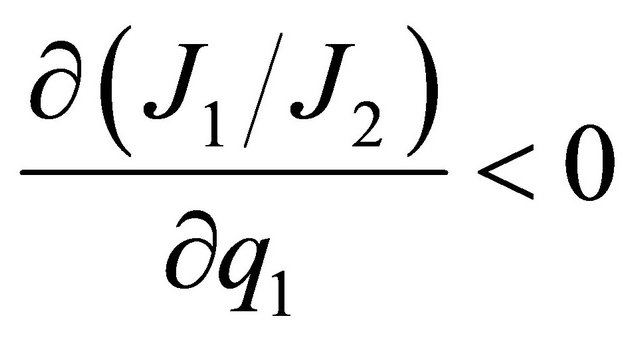 (13)
(13)
For  the first order conditions are:
the first order conditions are:
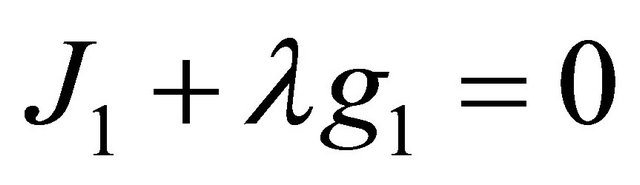

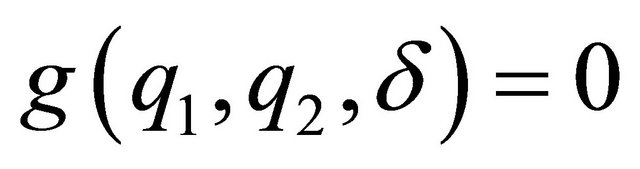
with 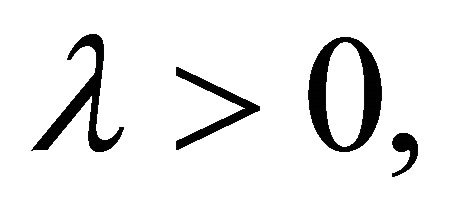 the multiplier of the problem of maximization. Thus, it is possible to deduce the following equation:
the multiplier of the problem of maximization. Thus, it is possible to deduce the following equation:
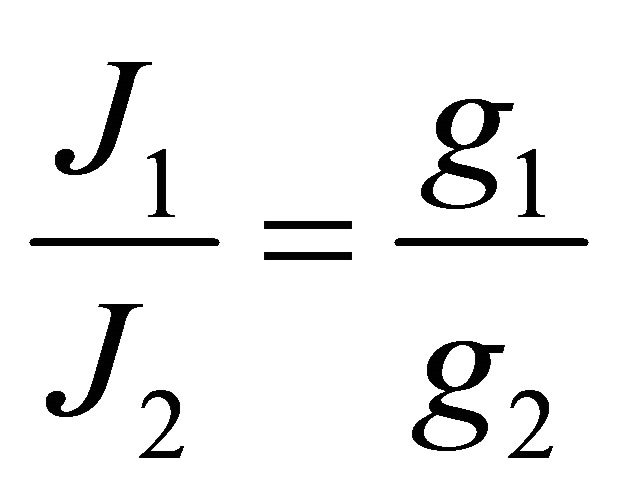 (14)
(14)
Differentiating with respect to , we obtain that:
, we obtain that:
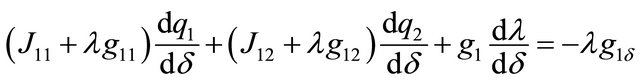
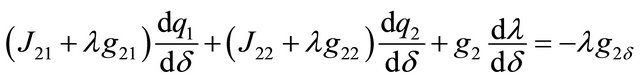
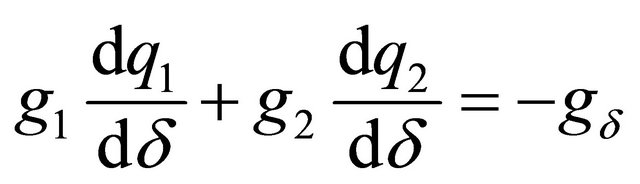
These equations can be written in matrix form as:

The matrix on the left hand side is the bordered Hessian. Applying Cramer’s rule it is possible to obtain the changes in 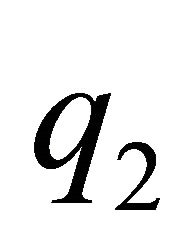 when
when  changes:
changes:
 (15)
(15)
where 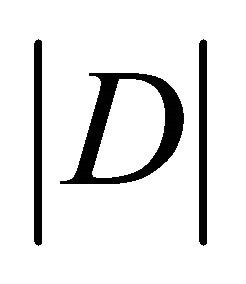 is the determinant of the bordered Hessian. The second order conditions of the maximization problem require that
is the determinant of the bordered Hessian. The second order conditions of the maximization problem require that  be positive.
be positive.
Therefore, the sign of 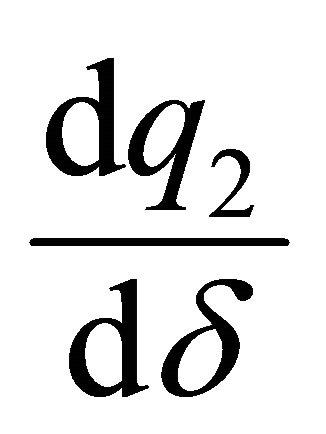 is determined by the sign of (15):
is determined by the sign of (15):
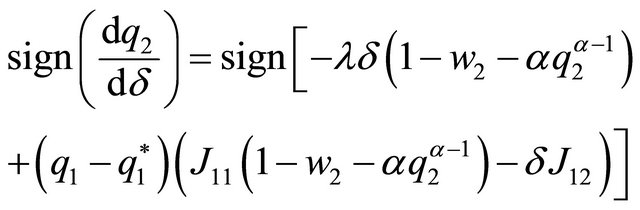 (16)
(16)
Given that 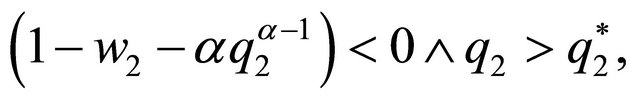 and under
and under
(13) and (14), we deduce that (16) is positive: 
Differentiating the restriction with respect to δ, we have:
 (17)
(17)
Thus, the sign of 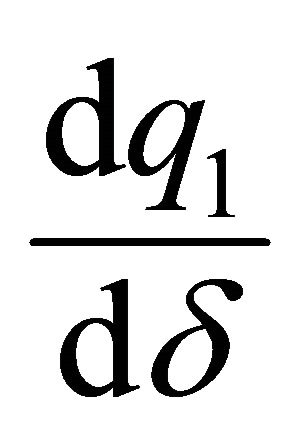 is the sign of the numerator:
is the sign of the numerator:
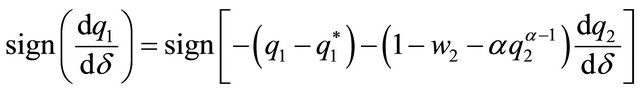
Given that
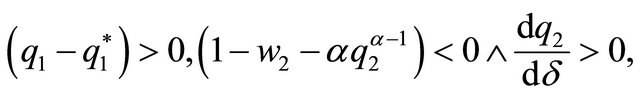
we deduce that
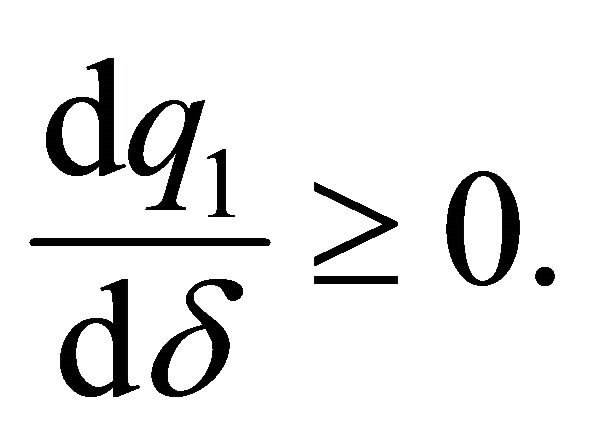 or
or 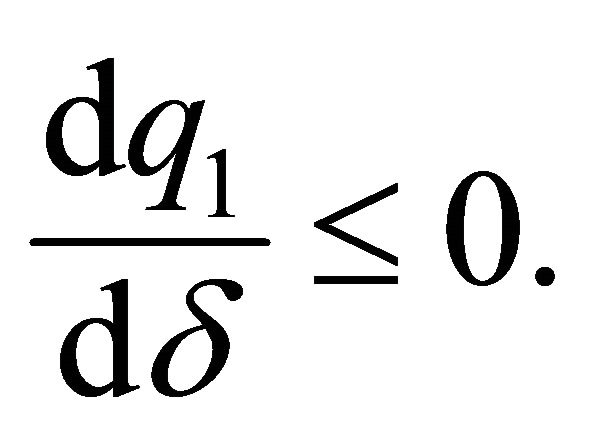
From (15) and (17), we can determine a value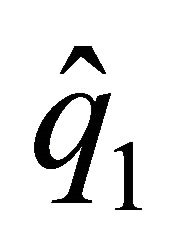 , with
, with 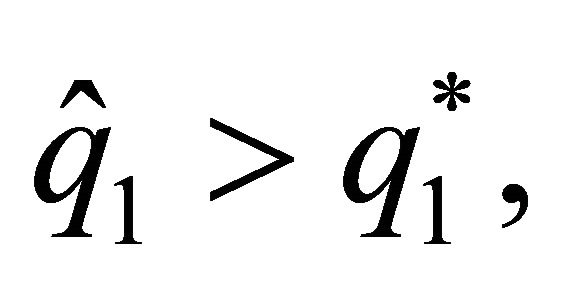 which represents the minimum value from which the relationship between the discount factor and the level of provision of the family good made by this agent becomes negative. So, when
which represents the minimum value from which the relationship between the discount factor and the level of provision of the family good made by this agent becomes negative. So, when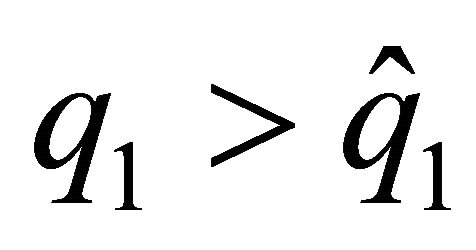 , we obtain that
, we obtain that 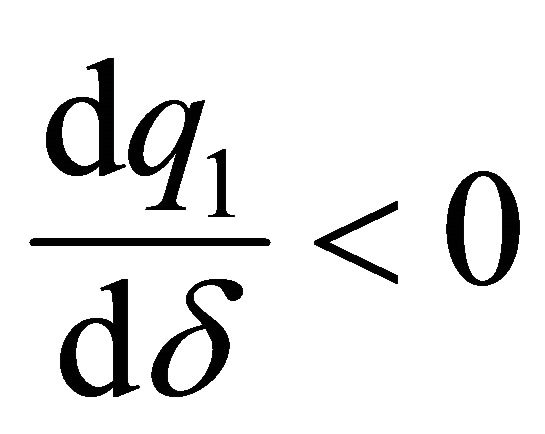 and when
and when 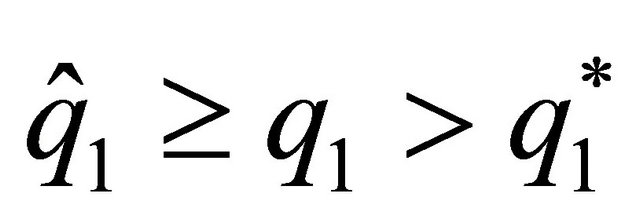 what we obtain is that
what we obtain is that 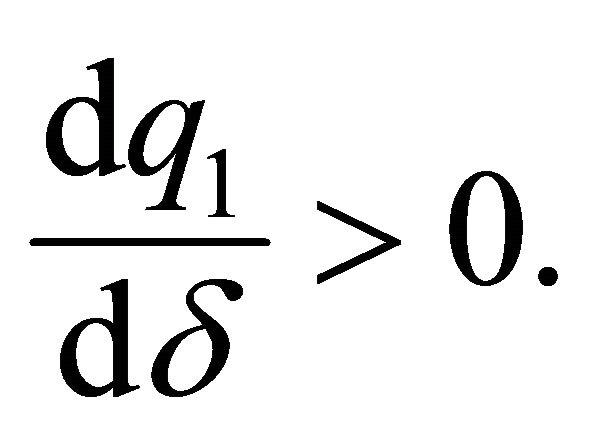
Proof of Corollary Applying the envelope theorem, we derive the utility function of both spouses with respect to 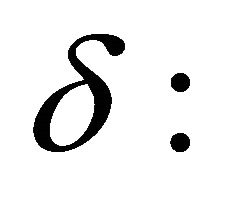
For spouse 1, we obtain:
 (18)
(18)
Taking into account (17), this expression takes the following form:
 (19)
(19)
Given that
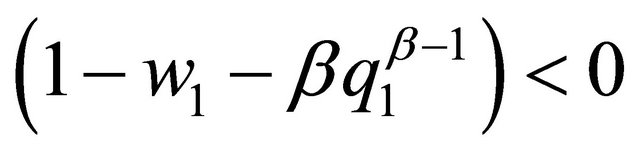 ,
, 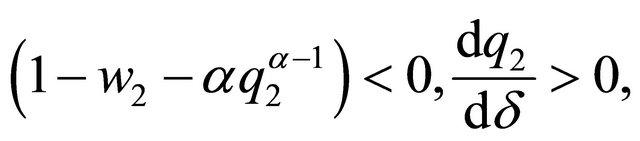
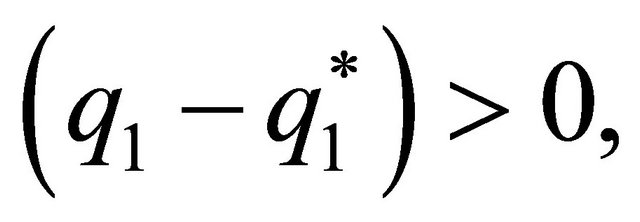
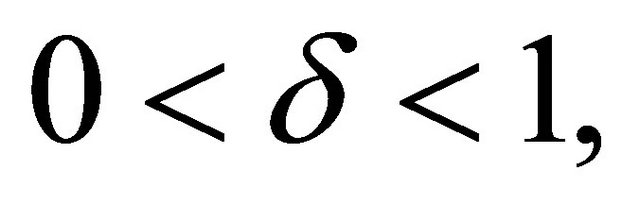

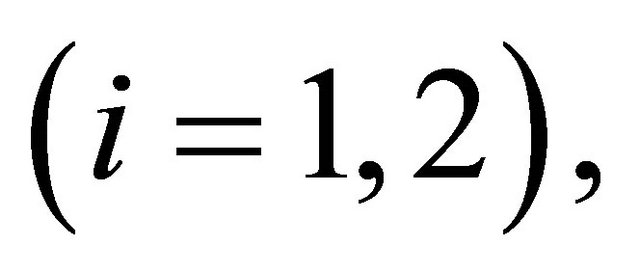 we deduce that:
we deduce that: 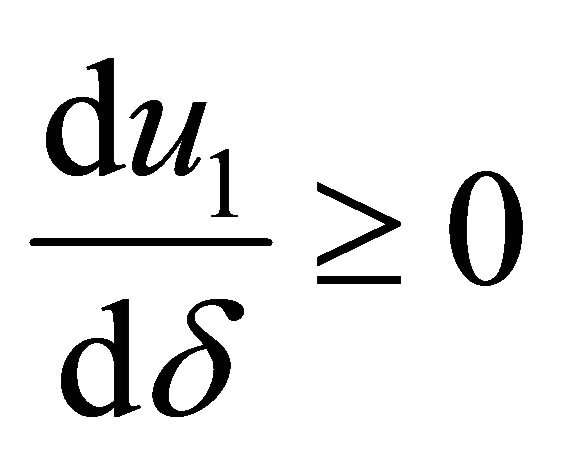 or
or 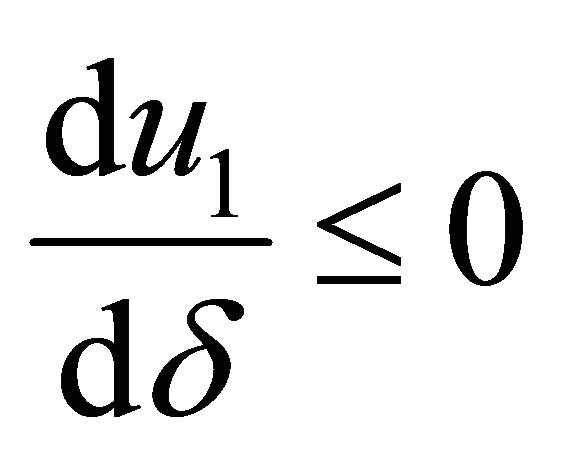
Analogously, given that 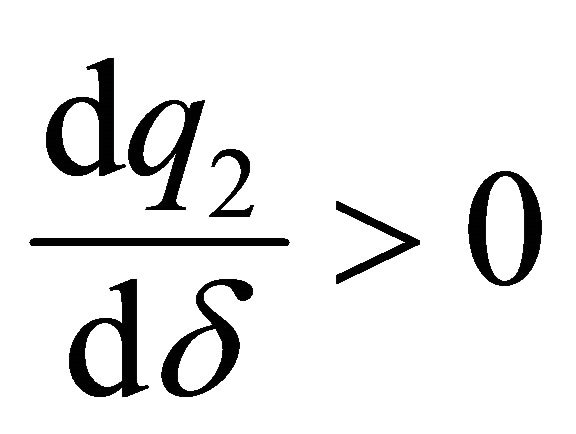 and with
and with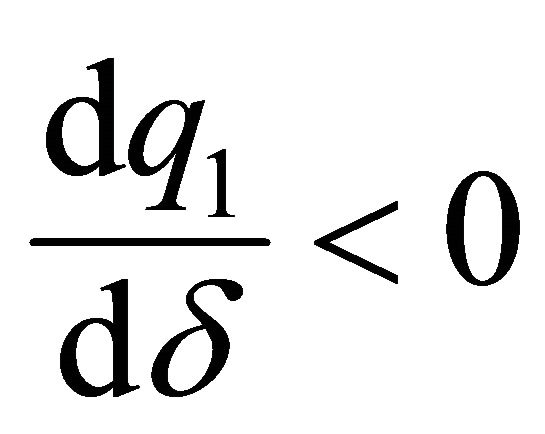 , we obtain that
, we obtain that  with
with . When
. When , we obtain that
, we obtain that 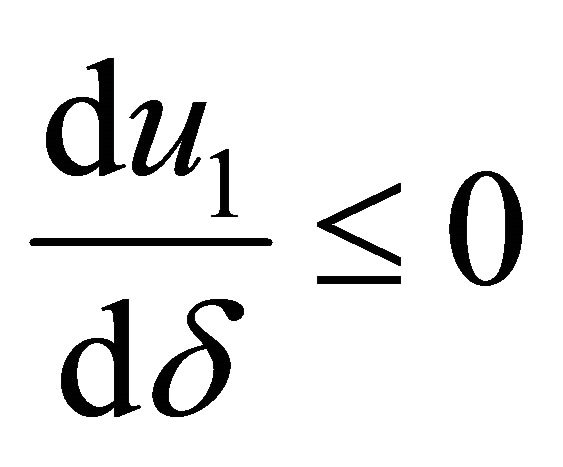 with
with  .
.
For spouse 2,
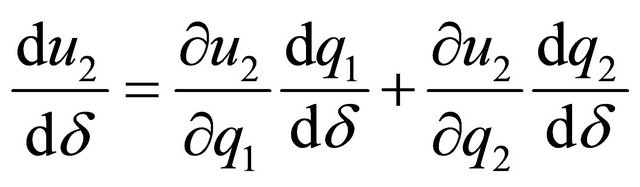
Introducing (17), we deduce that:
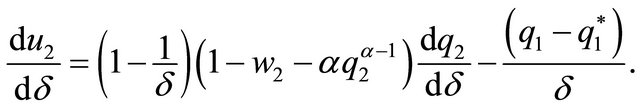
Analogously, we obtain that
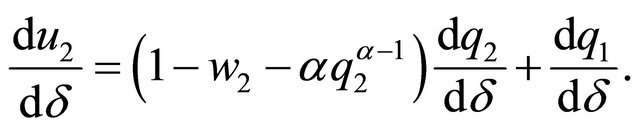
Given that 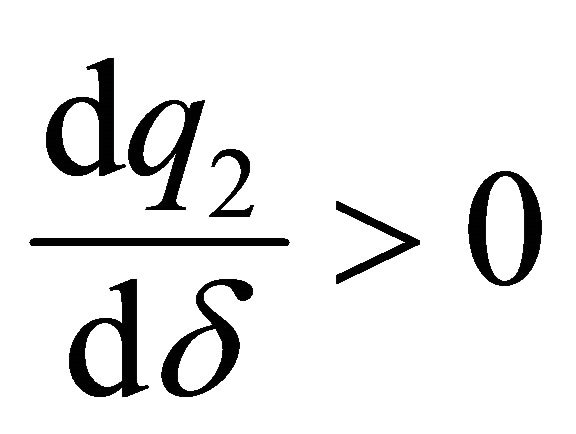 and with
and with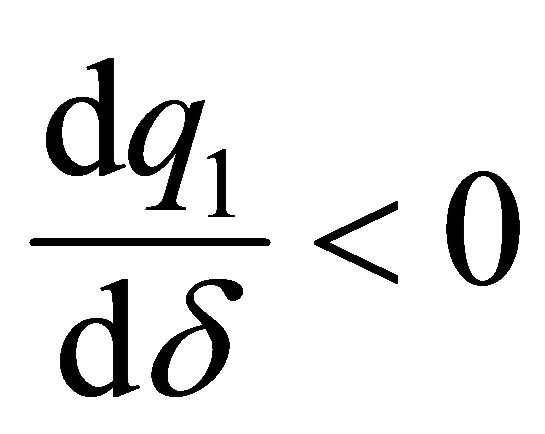 , we obtain that
, we obtain that  Remember that it is necessary that
Remember that it is necessary that 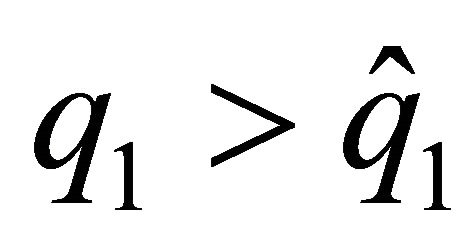
to obtain a negative relationship between the discount factor and the level of provision of the family good made by spouse 1. When , we obtain that
, we obtain that 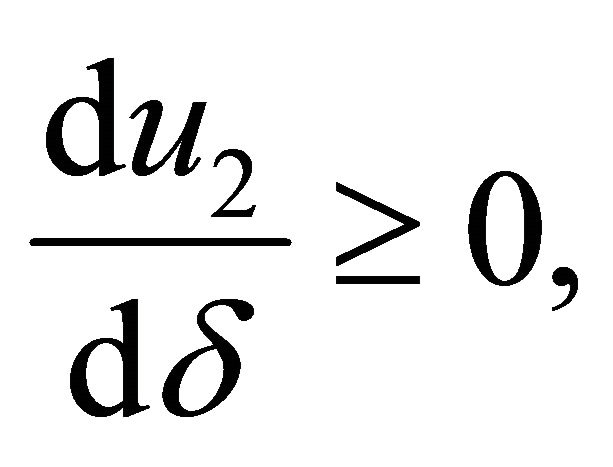 with
with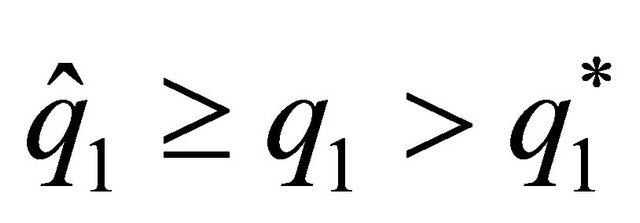 .
.
NOTES
1Note that sustainability here means the absence of incentives to deviate from the Nash bargaining solution.
2The discount factor of the leader is not a key element in this analysis, thus it is not necessary to observe gender differences in discounting (for a review of this literature see Benjamin et al. [13]).
3Note that, under the preferences specified above, the reaction functions for both spouses have null slope, and thus, the provision of the family good by both agents is strategically independent. As a consequence, the levels of consumption and the provision of the family good obtained in the Stackelberg equilibrium coincide with those obtained in a Nash equilibrium.
4This result differs from that obtained by Bucholz et al. [16]. However, note that, in our model, the type of Stackelberg equilibrium does not depend on the aggregate income of the spouses, or on the redistribution of income between spouses. This is due to the fact that the incomes of the agents are endogenously determined, and that one spouse cannot compensate the other spouse.
5Our approach is developed in an environment where marital partners have separate preferences, and are involved in a long-term relationship.
6This is not applicable to the situation of the standard case of Nash reversion, since, in this situation, decisions are taken simultaneously, and to obtain stationary paths it is necessary to include an additional inequality similar to that introduced for spouse 2, (10), but in this case it must also be established for spouse 1.
7This solution implicitly assumes a bargaining process resulting in the generalised bargaining solution (see Binmore et al. [18]; Harsanyi [19]).
8It is straightforward to deduce that under the structure of preferences used in this analysis, the provision of the family good is independent of the discount factor when we use the Cournot-Nash equilibrium as the threat point in the analysis.

