Journal of Mathematical Finance
Vol.05 No.02(2015), Article ID:56555,9 pages
10.4236/jmf.2015.52018
Duopolistic Competition and Capacity Choice with Jump-Diffusion Process
Danmei Chen1,2
1School of Finance, Shanghai University of Finance and Economics, Shanghai, China
2Basic Department, Shanghai Jianqiao University, Shanghai, China
Email: chenccc_008@163.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 April 2015; accepted 17 May 2015; published 22 May 2015
ABSTRACT
This paper studies the effects of sudden events on the optimal timing and capacity choice in a duopoly market. According to the characteristics of economic environment, we assume that the product demand follows geometric Brownian motion with a Poisson jump process. Under the settings, the firms face the risk of a sudden drop in demand which is caused by sudden events. We develop the real option game model to derive the investment equilibrium strategies. Moreover, the effects of sudden events on investment decisions are obtained by numerical analysis.
Keywords:
Investment Decisions, Competitive, Real Option Game, Jump-Diffusion Process

1. Introduction
We develop the real option game model to discuss the effects of sudden events on the optimal timing and capacity choice in a duopoly market. When sudden events occur, such as the financial crisis, economic policy from government, and the emergence of new products, discontinuous change in product demand appears. We use jump- diffusion process to capture the discontinuous changes of product demand.
Most real option game models suppose that the uncertainty variables such as asset price or product demand follow the geometric Brown motion (GBM) to describe the characteristics of continuous changes (e.g. Smets [1] ; Dixit and Pindyck [2] ; Grenadier [3] ; Weeds [4] ; Mason and Weeds [5] ).
However, the GBM cannot explain some important empirical features of asset price or product demand dynamics. Jorion [6] and Bates [7] discovered the presence of jumps in asset price through empirical research. Recent studies have pointed out the importance of allowing for jumps, or discontinuities of asset price or product demand due to the effects of random sudden events in the economic environment. Merton [8] assumed that the stock price follows a jump-diffusion process with Poisson jump to model sudden events. Kou [9] proposed a double exponential jump-diffusion model. Mason and Wilmot [10] investigated the potential presence of jumps in natural gas price. Ko et al. [11] established real option game model with jump process to investigate the effects of sudden events on investment timing. Pereira and Armada [12] assumed that the entrance of the hidden rivals follows a Poisson process. The project value of the positioned firm has a sudden drop as the hidden rivals enter the market. They presented a model suitable for investment decisions under a hidden competition environment. Pereira and Rodrigues [13] assumed that firms face the risk of demonopolization from government that can occur as a random or a certain event. They studied the optimal timing in finite-lived monopolies.
The large majority of real option game models focus on the investment timing without considering production capacity choice. However, in reality, production capacity decision is a key factor when one firm invests products. Few studies have considered the interaction between the investment timing and the production capacity in a real option framework. Besanko et al. [14] considered the investment decisions of the heterogeneous products under discrete time framework. Jou and Lee [15] assumed that all firms use the same investment strategy, obtaining the investment timing and the optimal capacity under imperfect competition. Huisman and Kort [16] provided a dynamic analysis of entry deterrence strategies, they discovered the leader overinvest in capacity in order to delay entry of the follower. The paper has close connection with these studies, which are extended by introducing the effects of sudden events and pre-emptive competition on the investment decisions. In this model, two firms are allowed to produce the homogeneous products; the product demand is assumed to obey the geometric Brown motion with a Poisson jump process. We discuss strategic investment decisions under duopolistic competition.
The remainder of the paper is organized as follows. Section 2 introduces the basic assumption of the real option game model. In Section 3, we derive the equilibrium strategies in a duopoly market. Section 4 exercises numerical analysis. Section 5 concludes the paper.
2. Basic Assumption of Real Option Game Model
In the section, we assume two firms have the chance to produce the homogeneous products in a duopoly market. Time is continuous and horizon is infinite. So every firm can defer the investment timing until the optimal moment to enter the market. The firm that enters first is known as the leader and the other as the follower. The product price at time t in market is given as follows:
 (1)
(1)
where 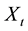 is the exogenous demand shock, Q is the total market output, unit production cost is c, so the total costs of production are cQ. Similar to Huisman and Kort [16] , every firm cannot adjust production capacity after entering the market and the two firms must make full use of production capacity. The exogenous demand shock is affected by sudden events of external market environment. Suppose that
is the exogenous demand shock, Q is the total market output, unit production cost is c, so the total costs of production are cQ. Similar to Huisman and Kort [16] , every firm cannot adjust production capacity after entering the market and the two firms must make full use of production capacity. The exogenous demand shock is affected by sudden events of external market environment. Suppose that 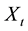 obey the geometric Brown motion with the Poisson jump process:
obey the geometric Brown motion with the Poisson jump process:
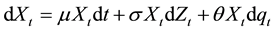
Among the above factors,  represents the drift rate,
represents the drift rate, 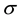 represents the volatility,
represents the volatility, 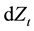 is the increment of a standard Brownian motion. We assume
is the increment of a standard Brownian motion. We assume 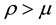 to ensure that the option is exercised within a finite period of time. We assume random sudden events follow the Poisson jump process of intensity
to ensure that the option is exercised within a finite period of time. We assume random sudden events follow the Poisson jump process of intensity . This means sudden events occur with probability
. This means sudden events occur with probability 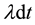 during the time interval dt. Sudden drop in product demand as the events occur.
during the time interval dt. Sudden drop in product demand as the events occur. 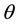 represents the deterministic amplitude of the downward jumps satisfying
represents the deterministic amplitude of the downward jumps satisfying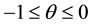 . Assume
. Assume 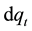 and
and 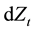 are independent, so
are independent, so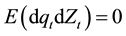 :
:
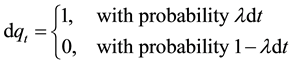
3. Investment Decisions in a Duopoly Market
In the section, we develop the model to determine the values and the investment decisions of two firms in a duopoly market, facing the risk of random sudden drop in product demand.
3.1. The Follower’s Value Function
We need to consider the game backwards. When the leader has invested the project, the follower can make his decisions optimally in response to capacity of the leader. Suppose that the leader has invested the project with capacity ql, the investment threshold and capacity of the follower are chosen as Xf and qf, so the investment costs are


According to Itô’s Lemma, the value of the follower 

The general solution of (1) is of the form:

Among them, 




Moreover, the value of the follower 



Condition (4) says that the value will be 0 if


Under these conditions, the value



where


We assume that the initial demand level is sufficiently low, the follower will not start production immediately. According to (7), the value of the follower

See from (10), 



Combining (8) and (11), we obtain the optimal threshold and the capacity of the follower:

Substitute (12) into (9) and (10), the value of the follower 

Let 



3.2. The Leader’s Value Function
When the follower is out of the market, the leader earns profits 
ters the market, the leader’s profits decreases to 
the leader is






The general solution of (15) is of the form:

The value of the leader 


If we apply (17), (18) to (16), 

where

Before the leader invests the project, the value of the leader 

The general solution of (21) is of the form:

In addition, the value of the leader 



Condition (24) says that:

If we apply (23), (24), (25) to (22), we obtain:

where


We assume that the initial demand level is sufficiently low, the leader will not start production immediately. To maximize the value, we apply (28), (29) to (27), and substitute (12) into (27), the value of the leader is calculated as:

3.3. Equilibrium
Here, in order to examine impacts of pre-emptive competition, we assume that the roles of the leader and the follower are designated exogenously. The follower enters the market only after the leader has entered. This means that one firm is designated as the leader beforehand. So, the risk of pre-emption is eliminated, two firms can delay their investment to maximize their values. When the initial demand is sufficiently low, we suppose the leader (follower) select the optimal capacity 



of the leader (follower) is denoted as 



Combining (28) and (31), we have:

So, by substituting (32) into (12), the optimal threshold and the capacity of the follower are given by:

Comparing (14) and (32), Proposition 1 is obtained.
Proposition 1. The investment threshold of the designated leader is the same as that of the monopolist.
The designated leader has valuable option to defer investment at the optimal threshold of the monopolist as he need not face the risk of being preempted.
However, two firms are allowed to invest first in reality. This means that firm roles are endogenous. So, the risk of pre-emption exists. We assume that the initial demand level is sufficiently low, two firms are induced to delay their investment. When firm roles are endogenous, according to Fudenberg and Tirole [17] , if one firm intends to invest at the threshold 






Proposition 2 describes the sequential equilibrium. For the proof of Proposition 2, see the Appendix.
Proposition 2. (sequential equilibrium). If the initial demand level is lower than








the optimal capacity

the optimal capacity 


Proposition 3, 4 describe the impacts of pre-emptive competition. The proofs are in Appendix.
Proposition 3. When the risk of pre-emption exists, the leader reduce its capacity to invest early, the follower increases its capacity to invest early. That is, 



Proposition 4. If the initial demand level is lower than


4. Numerical Results Analysis
4.1. The Impacts of Pre-Emptive Competition
The subsection describes the impacts of pre-emptive competition on the firms. The parameters are as follows:







Based on the given parameters, we calculate to obtain the optimal capacities and thresholds respectively as the roles of the firms are endogenous or exogenous:











Figure 1 further shows the relationship between the values of the two firms as the roles are endogenous or exogenous. The numerical analysis is based on the assumptions that the initial demand is less than

So, Figure 1 suggests the conclusions of Proposition 3, 4.
4.2. Sensitivity Analysis
In the subsection, we perform a comparative static analysis, focusing on the impacts of different parameter values such as the Poisson jump process of intensity λ, the deterministic amplitude of the jumps θ, the volatility
Table 1 illustrates the impacts of different values of λ. The parameters are as follows:






Figure 1. Values of the two firms.
λ. As we mentioned above, higher λ makes the investors reduce output to invest later. On the other hand, higher price which due to less output encourages the follower to invest earlier. As λ increases, the values of both the leader and the follower will decline.
Table 2 illustrates the impacts of different values of θ. The parameters are as follows:






Table 3 illustrates the impacts of different values of








5. Conclusions
In this paper, we examine the impact of sudden events on the investment timing and production capacity decisions of a firm that faces competition. We obtain the investment equilibrium strategies.
Table 1. Impacts of different values of λ.
Table 2. Impacts of different values of θ.
Table 3. Impacts of different values of σ.
We find that pre-emptive competition and sudden events have great influence on investment decisions; pre-emptive competition makes firms accelerate investment. Higher uncertainty for market demand increases the values of both the leader and the follower. When sudden events occur more frequently or product demand declines in greater magnitude, the values of both firms will decline.
This paper considers the case of two firms. Consequently, a natural idea is to consider the case of a number of firms. Future research can also be concerned with the application of a different random process, e.g., arithmetic Brownian motion.
Acknowledgements
This research is supported by NSFC (71271127, 10971127).
References
- Smets, F. (1991) Exporting versus FDI: The Effect of Uncertainty, Irreversibilities and Strategic Interactions. Working Paper, Yale University, New Haven.
- Dixit, A. K. and Pindyck, R.S. (1994) Investment under Uncertainty. Princeton University Press, Princeton.
- Grenadier, S.R. (1996) The Strategic Exercise of Options: Development Cascades and Overbuilding in Real Estate Markets. The Journal of Finance, 51, 1653-1679. http://dx.doi.org/10.1111/j.1540-6261.1996.tb05221.x
- Weeds, H. (2002) Strategic Delay in a Real Options Model of R&D Competition. The Review of Economic Studies, 69, 729-747. http://dx.doi.org/10.1111/1467-937X.t01-1-00029
- Mason, R. and Weeds, H. (2010) Investment, Uncertainty and Pre-Emption. International Journal of Industrial Organization, 28, 278-287. http://dx.doi.org/10.1016/j.ijindorg.2009.09.004
- Jorion, P. (1988) On Jump Processes in the Foreign Exchange and Stock Markets. Review of Financial Studies, 1, 427- 445. http://dx.doi.org/10.1093/rfs/1.4.427
- Bates, D.S. (1996) Jumps and Stochastic Volatility: Exchange Rate Processes Implicit in Deutsche Mark Options. Review of Financial Studies, 9, 69-107. http://dx.doi.org/10.1093/rfs/9.1.69
- Merton, R.C. (1976) Option Pricing When Underlying Stock Returns Are Discontinuous. Journal of Financial Economics, 3, 125-144. http://dx.doi.org/10.1016/0304-405X(76)90022-2
- Kou, S.G. (2002) A Jump-Diffusion Model for Option Pricing. Management Science, 48, 1086-1101. http://dx.doi.org/10.1287/mnsc.48.8.1086.166
- Mason, C.F. and Wilmot, N.A. (2014) Jump Processes in Natural Gas Markets. Energy Economics, 46, S69-S79. http://dx.doi.org/10.1016/j.eneco.2014.09.015
- Ko, C.-C., Lin, T.T. and Yang, C. (2011) The Venture Capital Entry Model on Game Options with Jump-Diffusion Process. International Journal of Production Economics, 134, 87-94. http://dx.doi.org/10.1016/j.ijpe.2011.02.016
- Pereira, P.J. and Armada, M.R. (2013) Investment Decisions under Hidden Competition. Economics Letters, 121, 228- 231. http://dx.doi.org/10.1016/j.econlet.2013.07.029
- Pereira, P.J. and Rodrigues, A. (2014) Investment Decisions in Finite-Lived Monopolies. Journal of Economic Dyna- mics and Control, 46, 219-236. http://dx.doi.org/10.1016/j.jedc.2014.07.003
- Besanko, D., Doraszelski, U., Lu, L.X. and Satterthwaite, M. (2010) Lumpy Capacity Investment and Disinvestment Dynamics. Operations Research, 58, 1178-1193. http://dx.doi.org/10.1287/opre.1100.0823
- Jou, J.B. and Lee, T. (2008) Irreversible Investment, Financing, and Bankruptcy Decisions in an Oligopoly. Journal of Financial and Quantitative Analysis, 43, 769-786. http://dx.doi.org/10.1017/S0022109000004282
- Huisman, K. and Kort, P.M. (2013) Strategic Capacity Investment under Uncertainty. Tilburg University, Tilburg.
- Fudenberg, D. and Tirole, J. (1985) Preemption and Rent Equalization in the Adoption of New Technology. The Review of Economic Studies, 52, 383-401. http://dx.doi.org/10.2307/2297660
Appendix
The proof for Proposition 2:
When pre-emptive competition exists, the follower makes his decisions reacting to the capacity of the leader. According to (28), we can obtain (36). According to (12), we can obtain (37).
The value is the same for both firms at the threshold

Simplifying the above equation, we conclude that (35) stands and 
The proof for Proposition 3:
We proof that when


Let









Substitute 


The proof for Proposition 4:
If



ing function of













