Journal of Mathematical Finance
Vol.3 No.1(2013), Article ID:28396,11 pages DOI:10.4236/jmf.2013.31011
Hedging with Stock Index Options: A Mean-Extended Gini Approach
1Department of Economics, Ben-Gurion University, Beer Sheva, Israel
2Department of Economics and Business Administration, Ariel University Center, Ariel, Israel
Email: shalit@bgu.ac.il, dorongre@Ariel.ac.il
Received October 16, 2012; revised November 21, 2012; accepted December 13, 2012
Keywords: Hedge Ratios; Systematic Risk; Basis Risk; Risk Aversion; Mean-Gini
ABSTRACT
One of the more efficient methods to hedge portfolios of securities whose put options are not traded is to use stock index options. We use the mean-extended Gini (MEG) model to derive the optimal hedge ratios for stock index options. We calculate the MEG ratios for some main stocks traded on the Tel Aviv Stock Exchange and compare them to the minimum-variance hedge ratios. Computed for specific values of risk aversion, MEG hedge ratios combine systematic risk with basis risk. Our results show that increasing the risk aversion used in the computation reduces the size of the hedge ratio, implying that less put options are needed to hedge away each and every security.
1. Introduction
In this paper we use the mean-extended Gini (MEG) model to derive optimal hedge ratios for portfolios with stock index options. Since their introduction in the earlier 1980’s, stock index futures and options have allowed investors to manage equity portfolios by hedging against systematic risk. The main practical issue is to determine the proper hedge ratios, i.e., the number of futures contracts or put options to be traded in order to insure the portfolio. Hedge ratios of stock index options are expected to reduce two types of risk: systematic risk of the portfolio and risk of futures hedging, for which reason it has become a major investment instrument.
The standard approach for reducing risk in futures hedging is to use minimum variance to maximize expected utility so as to determine the optimal hedge ratios. Another approach, which has been in practice for the past 15 years, is to use MEG hedge ratios. Contrary to minimum variance, MEG hedge ratios allow the incorporation of risk aversion intensity into the hedging coefficient. A comprehensive review of futures hedge ratios and, in particular, mean-Gini hedging can be found in Lien and Tse [1], and Chen, Lee and Shrestha [2]. MEG has also been used to investigate hedging effectiveness in futures commodities contracts by Shaffer [3], in FTSE contracts by Butterworth and Holmes [4], and in currency hedging by Shaffer and DeMaskey [5]. These papers confirm the superiority of the MEG model over the mean-variance model in futures hedging. Indeed, their results show that MEG hedge ratios achieve greater risk reduction for all classes of risk-averse investors.
There are several main reasons why the MEG model should be used to insure a portfolio. First, MEG allows the derivation of hedge ratios that comply with the necessary and sufficient conditions for stochastic dominance. As such, the MEG model ensures that the hedge ratio is included in the second degree stochastic dominance (SSD) efficient set (Cheung, Kwan, and Yip [6]). Second, MEG ratios remedy the failures incurred by the interdependence of the price index and the error terms. In particular, the Gauss-Markov conditions required by the ordinary-least-squares (OLS) regression model may be violated and the results will not be validated as optimal hedge ratios. Thus, MEG ratios are consistent estimators for minimum variance ratios (Shalit [7]). Third, if the probability distribution of the stock price index is not normal, as would be expected based on empirical investigations, the OLS coefficients will draw most of their statistical significance from the extreme observations whereas with MEG all observations contribute more evenly to the power of the estimates (Shalit and Yitzhaki [8]).
In the next section we derive the theoretical hedge ratios using a portfolio hedging model with stock index put options. Then in the third section, we present a primer on mean-Gini theory whose purpose is to show why the MEG model has been used in futures hedging. In the fourth section, we use the mean-Gini methodology to derive the MEG hedge ratios with stock index put options. In the fifth section, we apply this methodology to securities traded on the Tel-Aviv Stock Exchange and estimate the hedging ratios.
2. The Portfolio Insurance Model with Index Put Options
Consider a standard two-period model of portfolio insurance. An investor who holds a portfolio of n securities buys stock index put option contracts to limit the portfolio’s downside risk. We assume this is the only available strategy because, as it is the case in many financial markets, futures contracts and options on individual stocks are not readily traded or lack liquidity. The initial portfolio value is:
 (1)
(1)
where 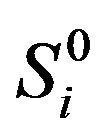 are the initial stocks prices and αi are their shares in the portfolio. To insure the portfolio against downside risk, the investor buys x index put options that expire at the end of the holding period at which time the hedged portfolio value is:
are the initial stocks prices and αi are their shares in the portfolio. To insure the portfolio against downside risk, the investor buys x index put options that expire at the end of the holding period at which time the hedged portfolio value is:
 (2)
(2)
where P0 and P1 are the initial and the final index put option prices and 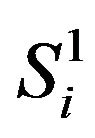 are the final stock prices.
are the final stock prices.
Our goal is to determine the hedge ratio that comprises the number of index contracts needed to insure the portfolio. When investors maximize expected utility of portfolio returns, the optimal hedge ratio can be obtained by using the mean-variance (MV) model since, as shown by Levy and Markowitz [9], MV approximates expected utility, regardless of the utility and the probability distribution. Furthermore, Benninga, Eldor and Zilcha [10,11] showed that the optimal hedge ratio is equal to the minimum-variance hedge ratio which is:
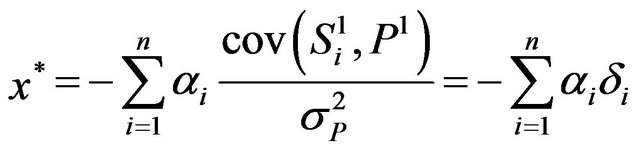 (3)
(3)
where δi is the regression coefficient of the share price on the index put option price as follows:
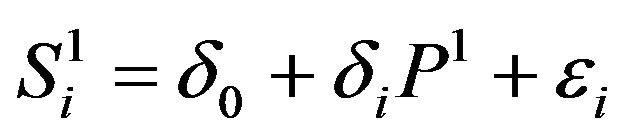 (4)
(4)
When the index put option is written on a wider market index, the hedge ratio can be decomposed into two elements. The first is the standard systematic risk βi and the second is the sensitivity of the index to changes in the put option prices, or the inverse of the put option delta. Indeed from Equation (4), the optimal hedge ratios δi are derived as:
 (5)
(5)
where I is the market index. The systematic risk βi is obtained by regressing the share price over the market index I. The index put option delta, Δ, is the rate of change of the put option with respect to the market index. Since the put option delta is identical for all assets in the portfolio, it does not affect the hedge ratio when the shares in the portfolio get changed.
The systematic risk βi used for the hedge ratio is slightly different from the usual definition of beta because it is obtained by regressing the stock prices on the index underlying the put option, which is done as follows:
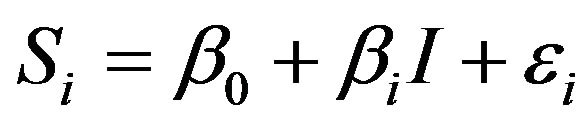 (6)
(6)
For the hedge ratio to be optimal the regression model must be valid, i.e., I and εi must be statistically independent. Since this condition may be violated, we propose to apply the MEG model to hedging in portfolio insurance. To understand the rationale of using this model, we begin with a brief review of the mean-Gini theory.
3. A Primer on Mean-Gini
Mean-Gini (MG) theory was originally developed by Yitzhaki [12,13]. Afterwards it was applied to finance by Shalit and Yitzhaki [14] as an alternative model to MV for evaluating systematic risk and constructing optimal portfolios that are consistent with expected utility maximization and stochastic dominance. MG presents robust results when MV is bound to fail, in particular, when assets are not normally distributed or when the regression used to estimate betas by ordinary least-squares provide biased estimators (Shalit and Yitzhaki [8]). Furthermore, MEG allows for the introduction of risk aversion differentiation into the estimation of systematic risk (GregoryAllen and Shalit [15]). For these reasons, the MEG model has been used to estimate optimal hedge ratios in futures markets (see Lien and Tse (2002) [1] and Chen, Lee, and Shrestha, [2]).
The Gini coefficient is a measure of dispersion used mainly in income inequality where the index is related to the Lorenz curve. In finance, it quantifies risk similarly to the role played by the variance as a measure of risk. Gini’s mean difference is defined as half the expected value of the distance between all pairs of returns. For portfolio returns w, it is written as:
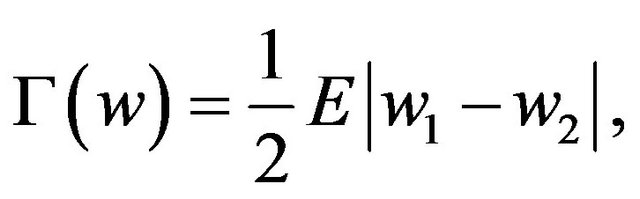 (7)
(7)
where w1 and w2 are independent realizations of the portfolio returns. This definition of the Gini can be developed into the following more practical representation that is commonly used in financial applications1:
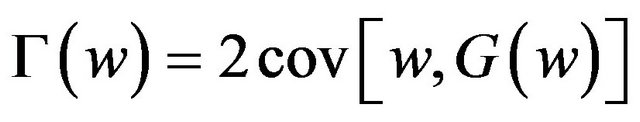 (8)
(8)
where G is the cumulative probability distribution of w. The Gini is a dispersion statistic that measures risk the same way the standard deviation evaluates risk. Even more advantageous to risk analysis is the extended Gini that allows specifying risk aversion intensity in the dispersion statistic. The extended Gini coefficient of portfolio w is defined as:
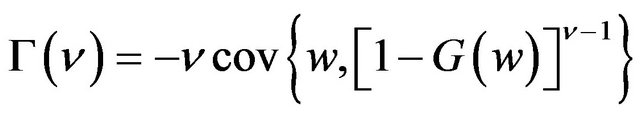 (9)
(9)
where ν is the extended Gini parameter associated with risk aversion. This parameter expresses the extent to which the lower realizations relative to the highest returns are weighted in order to evaluate risk. As investors become more averse to risk, they worry significantly more about lower returns, thus giving them comparatively more weight than that given to the higher returns when computing the measure of dispersion. The parameter of risk aversion ν ranges from 1 (representing a risk neutral investor) to infinity (for the most risk-averse investor exemplified by the max-min individual)2. In particular for n = 2, the standard Gini coefficient is obtained as in Equation (8).
The main advantage of MEG theory stems from the necessary and sufficient conditions for stochastic dominance which state that portfolio A is preferred to portfolio B for all risk-averse investors if
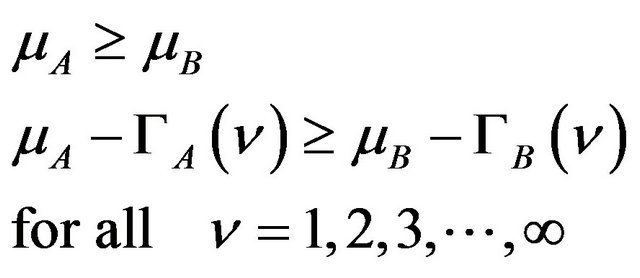 (10)
(10)
where mA, mB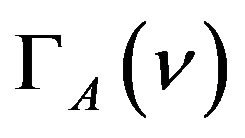 , and
, and 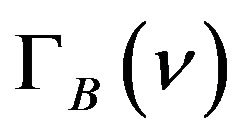 are the means and the extended Ginis of portfolio A and B, respectively. It follows from Equation that maximizing mα ‒ Gα for all portfolios a provide investors whose risk aversion parameter is n with their MEG efficient frontier. As an alternative, financial analysts sometimes minimize the extended Gini of the portfolio G(n) subject to a given mean return, as done in Shalit and Yitzhaki [17].
are the means and the extended Ginis of portfolio A and B, respectively. It follows from Equation that maximizing mα ‒ Gα for all portfolios a provide investors whose risk aversion parameter is n with their MEG efficient frontier. As an alternative, financial analysts sometimes minimize the extended Gini of the portfolio G(n) subject to a given mean return, as done in Shalit and Yitzhaki [17].
4. The Mean-Extended Gini Hedging Methodology
The MEG model in futures hedging is rooted in research papers that advocate the use of Gini methods in futures markets (Cheung, Kwan and Yip [6]; Hodgson and Okunev [18]; Kolb and Okunev [19] [20]; Lien and Luo [10]; and Shalit [7]). Some of the more comprehensive reviews of MEG in futures markets appear in Lien and Tse [1] and Chen, Lee, and Shrestha [2].
Many methods are used to estimate MEG hedging ratios, all of which are based on minimizing the extended Gini of the hedged portfolio subject to the mean return. The problem resides in calculating the extended Gini as the covariance of the portfolio return and its cumulative probability distribution. Kolb and Okunev [19,20] used the rank of the returns as an empirical distribution and derived the minimizing Gini hedge ratios by means of a search method. On the other hand, Lien and Luo [21] improved the estimation of the cumulative probability function using a smoothing kernel method while maintaining the numerical searching procedure. Shalit [7] provided an analytical solution to the MEG hedge ratios based on the instrumental variable (IV) regression. Later, Lien and Shaffer [22] showed that Shalit [7] had erred when he assumed identical rankings for the hedged portfolios returns and the futures prices in order to estimate the hedge ratio.
However, the portfolio insurance model is different from the futures hedging model because the index put option is written on market index in the same manner that the beta CAPM is obtained as the regression of the risky asset on the market portfolio. The portfolio hedging model is developed as follows. Consider investors with a risk-aversion coefficientn. The optimal mean-extended Gini hedge ratio for an index option is obtained by maximizing the mean minus the extended Gini of the hedged portfolio as follows:
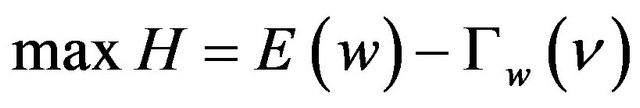 (11)
(11)
where 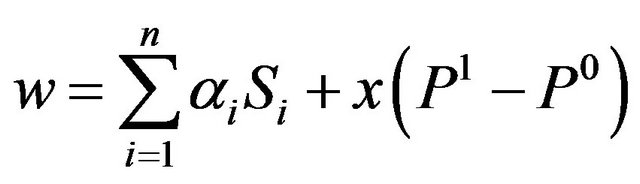 and
and
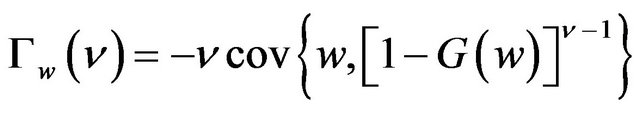 .
.
We then differentiate Equation with respect to αi and x. Since the extended Gini is homogenous of degree one in the αi and x we now apply Euler’s theorem to express the Gini as:
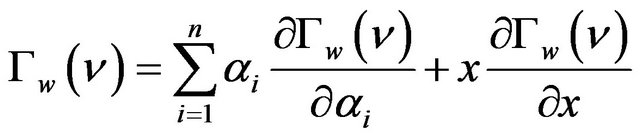 (12)
(12)
The result yields:
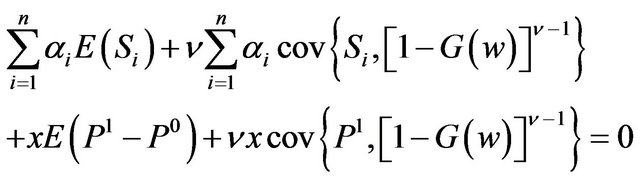 (13)
(13)
or
 (14)
(14)
As the covariance remains unchanged when subtracting a constant, we obtain the optimal hedge as that which brings the extended Gini of the portfolio to zero:
 (15)
(15)
or
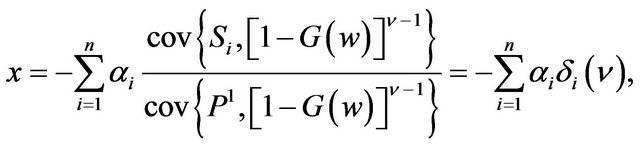 (16)
(16)
where δi(ν) is the optimal MEG hedge ratio that uses index options for an investor with risk aversion coefficient ν. The question now is how to evaluate the ratio using financial data. As w are returns of a well-diversified portfolio of many securities and P is a put option written on a wider market index, the assumption that w and P have the same probability distribution as the market index I is valid one. Hence, one can write Equation as
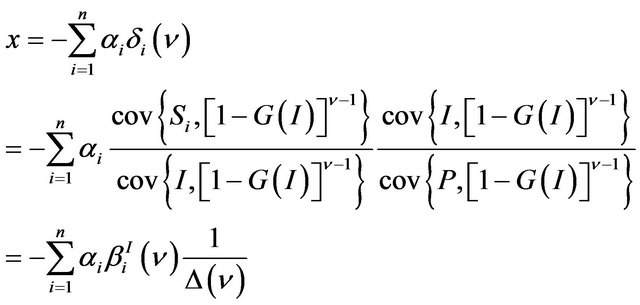
(17)
where the put option delta Δ(ν) is expressed in terms of MEG. We obtain the optimal MEG hedge ratio using index options in two steps. First, the 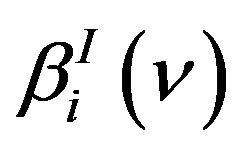 are found as the mean-extended Gini regression coefficients of the stock returns over the market index for a specific ν. These are basically IV regression coefficients where the instrument is
are found as the mean-extended Gini regression coefficients of the stock returns over the market index for a specific ν. These are basically IV regression coefficients where the instrument is 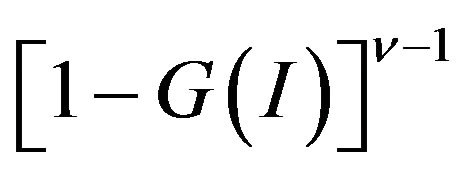 for each ν. The cumulative probability distribution G(I) is estimated by using the rank of the market index I. Second, the Δ(ν) are obtained from the IV regressions of the put option price over the market index with each one using the appropriate instrument
for each ν. The cumulative probability distribution G(I) is estimated by using the rank of the market index I. Second, the Δ(ν) are obtained from the IV regressions of the put option price over the market index with each one using the appropriate instrument  for the different ν.
for the different ν.
The main issue in using MEG hedge ratios is to check whether these ratios differ statistically from MV ratios. Indeed, if the ratios are basically the same there is no need to calculate MEG ratios and the MV hedging ratios will satisfy all risk-averse investors. A natural question that arises is how to assess whether MEG ratios differ from MV ratios? Two avenues may be pursued: The first is theoretical since, as shown by Shalit [7], MEG ratios subside to the MV ratio if stock returns are normally distributed. Then, the issue is to test the normality of the financial returns. The second is an econometric approach that consists of applying Hausman’s [23] specification error test to examine whether the MEG ratios differ from the MV ratio. The Hausman [23] test uses the statistic:
 , (18)
, (18)
where  is the variance of MV beta and
is the variance of MV beta and 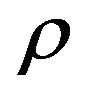 is the correlation between the stock return and the instrumental variable. The m(ν) statistic is distributed Chisquare with one degree of freedom.
is the correlation between the stock return and the instrumental variable. The m(ν) statistic is distributed Chisquare with one degree of freedom.
5. Data and Estimation Results
We conducted our research using data from the Tel-Aviv Stock Exchange (TASE) since no stock options on individual securities are traded there. The only way investors can hedge individual stocks is by holding positions in stock index options and futures although some firms whose shares are listed overseas have options traded on their stocks, (for example, Teva Pharmaceuticals, which is listed on the TASE and NASDAQ, has options traded on AMEX).
The sample consists of 1080 daily returns of 57 stocks traded on the TASE from August 1, 1993 until December 31, 1997, together with 14,340 observations of put options written on the TASE 25 stock index for the same time period. The Tel Aviv Stock Exchange began to officially trade stock index options on August 1, 1993, hence the sample period has some historical significance. The TASE 25 stock index is a capitalization-weighted index of the 25 stocks with the highest market values traded on the exchange. Options contracts on the TASE 25 stock index are traded daily from Sunday through Thursday. The contracts are quoted in New Israeli Shekels (NIS) at 100 NIS times the TASE 25 level.
Our goal is to estimate the 57 stocks hedge ratios for the TASE25 options contracts as expressed by Equation (5). First, we calculate the systematic risks for all 57 stocks using both the MV and the MEG approach for several coefficients or risk aversion ν ranging from 2 to 20. This is done by estimating Equation (6), and then regressing securities daily returns on the daily returns of the TASE 25 stock index using OLS and MEG (IV) regressions. Then, to test whether the MEG betas are statistically different from the MV beta we compute Hausman’s statistic to see whether this result depends on the normality distribution of the stock returns. We test for normality of stock returns by using the standard JarqueBera statistic.
The systematic risk coefficients for all the firms are presented in Table 1. For the major stocks traded on the TASE, the betas vary around 1 for the MV and the MEG models. To what extent the MEG betas differ from the MV beta depends upon the Hausman statistic reported below the coefficient for each MEG hedge. If the Hausman statistic is greater than 3.84 the MEG beta is statistically different (at 5%) from the MV hedge ratio. In geTable 1. MV and MEG betas on the TASE (Daily returns 1/08/1993-31/12/1997).

Continued

Continued
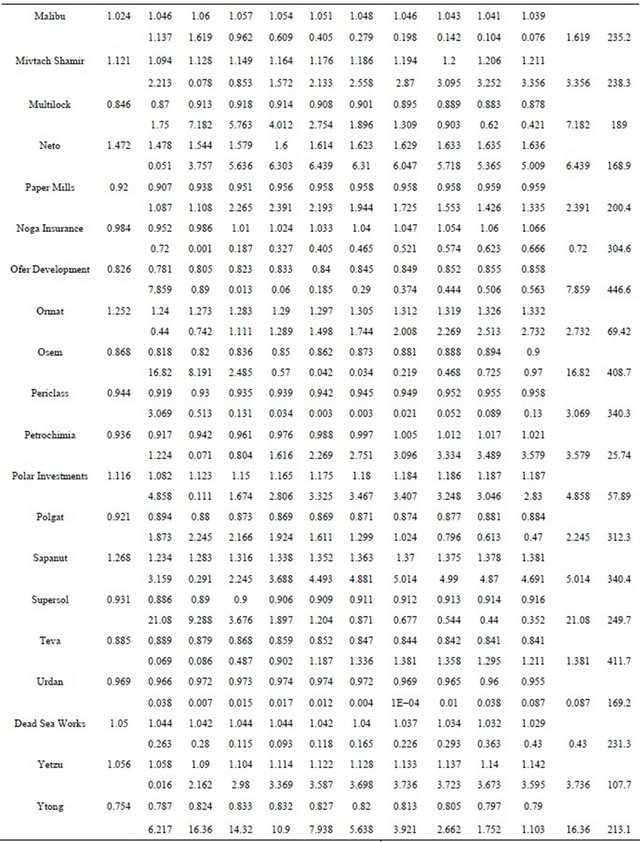
neral, the MEG systematic risk coefficients are greater than the MV beta and they increase as the risk aversion parameter increases from n = 2 to n = 20. This is commonly the case when the Hausman statistic shows that the MEG beta is statistically different from the MV beta. We can see from the maximum Hausman statistic, only 33 stocks from a total of 57 have at least one MEG beta that significantly differs from the MV hedge ratio. The Hausman statistic is not as large as one would expect for non-normally distributed stock returns. Indeed, as shown by the Jarque-Bera statistic being greater than 10, the hypothesis that all stock returns follow a normal distribution is rejected. Nevertheless, using MEG betas instead of the MV beta allows us to account for specific risk aversion.
The next step is to estimate delta Δ as the rate of change of the put option price with respect to the stock market index as shown in Equations (5) and (17). To account for changes in the exercise index price and the maturity date, we include these variables in the regression. The regression results are shown in the top three rows (Equation A) of Table 2. The index put option delta, Δ, estimated for the entire period, is −0.425. As shown in Equation (5), the hedge ratios are obtained by dividing the systematic risk by delta. In the MEG model, the hedge ratios as shown in Equation (17) must account for the differentiated risk aversion, ν. Hence, we estimate D(ν) as follows. First, we account for the changes in exercise price as well as in the exercise date by running a regression model of the put option price over these variables (see the bottom rows (Equation B) of Table 2). Then, we use the regression residuals of Equation B to calculate Δ(ν) as
 (19)
(19)
The results are shown in Table 3 for the various values of ν used in the research, together with the Δ calculated for the MV model. We can see that D(ν), the rates of change of the put option with respect to the market index, increase as the risk aversion parameter increases and that they all are greater than the D implied by MV. This is an expected result for the stock market index.
Now we can calculate the hedge coefficients for each security and for each coefficient of risk aversion n by dividing the betas with the appropriate D(ν) following Equation (17). The hedge ratios presented in Table 4 show how investors can evade the two types of risks incurred by holding a stock portfolio, namely the standard systematic risk and the basis risk of hedging the portfolio. By analyzing Table 4 we see why this approach is different from what we have ever seen in hedge ratios. For most securities, increasing risk aversion as expressed by n reduces the size of the ratio, implying that a smaller number of put options is needed to hedge each and every security. This is an unexpected result that can be attributed to the combination of the two risks factors (systematic risk and basis risk) and taking into account the risk aversion parameter.
6. Conclusion
As calculated in our paper, we have shown the advantages of using mean-extended Gini hedge ratios versus the standard mean-variance hedge ratios. Since these ratios combine systematic risk and the basis risk for a wide range of risk aversion coefficients, our results indicate that the hedge coefficients can accurately measure the number of stock index options needed to hedge securities in a diversified portfolio. The standard meanvariance hedge ratios consider only systematic risk and are insensitive to the investor risk aversion differentials. We have presented a procedure to obtain optimal MEG hedge
Table 2. The put option index regression equation.
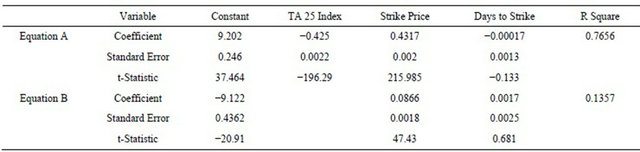
Dependent variable: Put price. Number of observations: 14,339.
Table 3. Estimates of Δ(ν) computed with the residuals of Equation B.

Table 4. MEG and MV hedge coefficients δ for each stock and for each risk aversion coefficient.
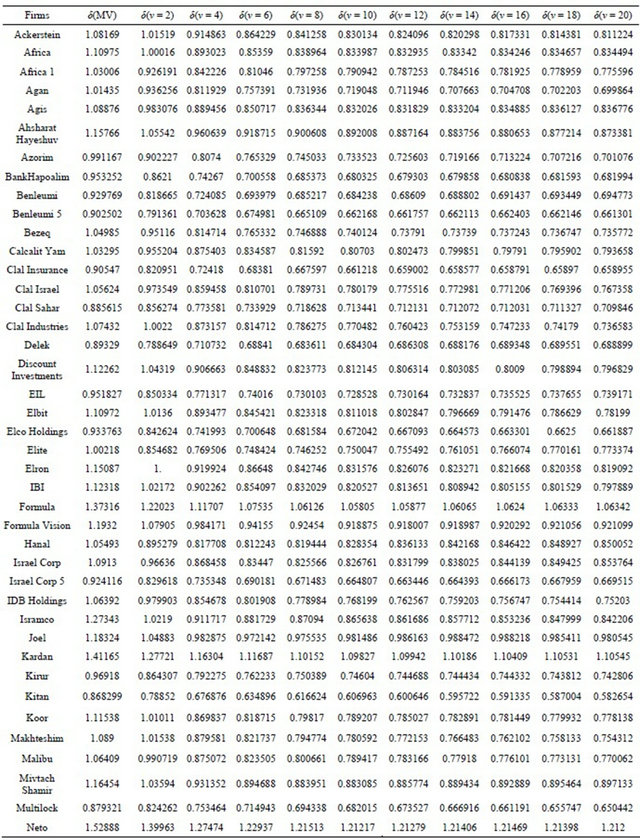
Continued
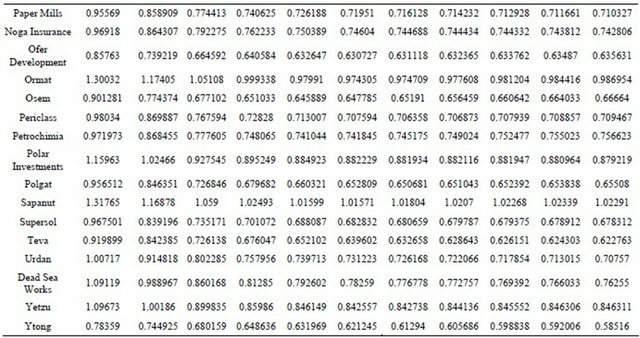
ratios. First, the analyst needs to establish the relevant risk aversion parameter for investors and portfolios managers to be used for the extended Gini. For a mild risk aversion, a parameter of n of about 2 can be used. For higher risk-averse investors, parameters of n greater than 4 is deemed appropriate and for extremely high riskaverse investors a parameter of n that are greater than 16 are necessary. Second, for each risk aversion n and for each stock the MEG systematic risk is to be estimated. Finally, for each risk aversion parameter n the delta option parameter Δ expressed as the rate of change of the put option price with respect to the stock market index is estimated. The MEG hedge ratios are thus individually tailored for each stock and for each type of investors. For most analyzed securities of the Tel Aviv Stock Exchange, increasing risk aversion reduces the hedge ratio entailing that less put options are needed to circumvent systematic risk and basis risk for a given the risk aversion.
REFERENCES
- D. Lien and Y. K. Tse, “Some Recent Developments in Futures Hedging,” Journal of Economic Surveys, Vol. 16, No. 3, 2002, pp. 357-396. doi:10.1111/1467-6419.00172
- S. S. Chen, C. F. Lee and K. Shrestha, “Futures Hedge Ratios: A Review,” The Quarterly Review of Economics and Finance, Vol. 43, No. 3, 2003, pp. 433-465. doi:10.1016/S1062-9769(02)00191-6
- D. Shaffer, “Estimating the Gini Hedge Ratio,” Managerial Finance, Vol. 29, No. 1, 2003, pp. 73-83. doi:10.1108/03074350310768256
- D. Butterworth and P. Holmes, “The Hedging Effectiveness of UK Stock Index Futures Contracts Using an Extended Mean Gini Approach: Evidence for the FTSE100 and FTSE Mid250 Contracts,” Multinational Finance Journal, Vol. 9, No. 3-4, 2005, pp. 131-160.
- D. Shaffer and A. DeMaskey, “Currency Hedging Using the Mean-Gini Framework,” Review of Quantitative Finance and Accounting, Vol. 25, No. 2, 2005, pp. 125-137. doi:10.1007/s11156-005-4245-9
- S. Cheung, C. Kwan and P. Yip, “The Hedging Effectiveness of Options and Futures: A Mean-Gini Approach,” Journal of Futures Markets, Vol. 10, No. 1, 1990, pp. 61-73. doi:10.1002/fut.3990100106
- H. Shalit, “Mean-Gini Hedging in Futures Markets,” Journal of Futures Markets, Vol. 15, No. 6, 1995, pp. 617- 635. doi:10.1002/fut.3990150603
- H. Shalit and S. Yitzhaki, “Estimating Beta,” Review of Quantitative Finance and Accounting, Vol. 18, No. 2, 2002, pp. 95-118. doi:10.1023/A:1014594617251
- H. Levy and H. M. Markowitz, “Approximating Expected Utility by a Function of Mean and Variance,” American Economic Review, Vol. 69, No. 3, 1979, pp. 308-317.
- S. Benninga, R. Eldor and I. Zilcha, “Optimal Hedging in the Futures Market under Price Uncertainty,” Economics Letters, Vol. 13, No. 2-3, 1983, pp. 155-159. doi:10.1016/0165-1765(83)90076-9
- S. Benninga, R. Eldor and I. Zilcha, “The Optimal Hedge Ratio in Unbiased Futures Markets,” Journal of Futures Markets, Vol. 4, No. 2, 1984, pp. 155-159. doi:10.1002/fut.3990040206
- S. Yitzhaki, “Stochastic Dominance, Mean-Variance, and Gini’s Mean Difference,” American Economic Review, Vol. 72, No. 1, 1982, pp. 178-185.
- S. Yitzhaki, “On an Extension of the Gini Inequality Index,” International Economic Review, Vol. 24, No. 3, 1983, pp. 617-628. doi:10.2307/2648789
- H. Shalit and S. Yitzhaki, “Mean-Gini, Portfolio Theory and the Pricing of Risky Assets,” Journal of Finance, Vol. 39, No. 5, 1984, pp. 1449-1468. doi:10.1111/j.1540-6261.1984.tb04917.x
- R. B. Gregory-Allen and H. Shalit, “The Estimation of Systematic Risk under Differentiated Risk Aversion,” Review of Quantitative Finance and Accounting, Vol. 12, No. 2, 1999, pp. 135-157. doi:10.1023/A:1008348104882
- S. Yitzhaki, “More than a Dozen Alternative Ways of Spelling Gini,” Research in Economic Inequality, Vol. 8, 1998, pp. 13-30.
- H. Shalit and S. Yitzhaki, “The Mean-Gini Efficient Frontier,” Journal of Financial Research, Vol. 28, No. 1, 2005, pp. 59-75. doi:10.1111/j.1475-6803.2005.00114.x
- A. Hodgson and J. Okunev, “An Alternative Approach for Determining Hedge Ratios for Futures Contracts,” Journal of Business Finance and Accounting, Vol. 19, No. 2, 1992, pp. 211-224. doi:10.1111/j.1468-5957.1992.tb00620.x
- R. W. Kolb and J. Okunev, “An Empirical Evaluation of the Extended Mean-Gini Coefficient for Futures Hedging,” Journal of Futures Markets, Vol. 12, No. 2, 1992, pp. 177-186. doi:10.1002/fut.3990120206
- R. W. Kolb and J. Okunev, “Utility Maximizing Hedge Ratios in the Extended Mean-Gini Framework,” Journal of Futures Markets, Vol. 13, No. 6, 1993, pp. 597-609. doi:10.1002/fut.3990130603
- D. Lien and X. Luo, “Estimating the Extended Mean-Gini Coefficient for Futures Hedging,” Journal of Futures Markets, Vol. 13, No. 6, 1993, pp. 665-676. doi:10.1002/fut.3990130607
- D. Lien and D. Shaffer, “A Note on Estimating the Minimum Extended Gini Hedge Ratio,” Journal of Futures Markets, Vol. 19, No. 1, 1999, pp. 101-113. doi:10.1002/(SICI)1096-9934(199902)19:1<101::AID-FUT5>3.0.CO;2-Z
- J. A. Hausman, “Specification Tests in Econometrics.” Econometrica, Vol. 46, No. 6, 1978, pp. 1251-1271. doi:10.2307/1913827
NOTES
1See Yitzhaki [16] for the numerous representations of the Gini.
2See Butterworth and Holmes [4] for an illustration of the risk aversion parameter used in the extended Gini.

