Open Journal of Statistics
Vol.06 No.06(2016), Article ID:72737,12 pages
10.4236/ojs.2016.66089
Some Group Runs Based Multivariate Control Charts for Monitoring the Process Mean Vector
Mukund Parasharam Gadre1, Vikas Chintaman Kakade2
1Department of Statistics, Savitribai Phule Pune University, Pune, India
2Department of Statistics, Tuljaram Chaturchand College, Baramati, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 10, 2016; Accepted: December 10, 2016; Published: December 14, 2016
ABSTRACT
In this article, we propose two control charts namely, the “Multivariate Group Runs’ (MV-GR-M)” and the “Multivariate Modified Group Runs’ (MV-MGR-M)” control charts, based on the multivariate normal processes, for monitoring the process mean vector. Methods to obtain the design parameters and operations of these control charts are discussed. Performances of the proposed charts are compared with some existing control charts. It is verified that, the proposed charts give a significant reduction in the out-of-control “Average Time to Signal” (ATS) in the zero state, as well in the steady state compared to the Hotelling’s T2 and the synthetic T2 control charts.
Keywords:
CRL Chart, Hotelling’s T2 Chart, Synthetic T2 Chart, Average Time to Signal (ATS), Zero State ATS, Average Run Length (ARL)

1. Introduction
In many industrial processes, quality of the product may depend on two or more quality characteristics (may be dependent), which need to be controlled and monitored simultaneously. In the last decade or two, various multivariate procedures have been developed for simultaneous monitoring of such characteristics. Most of these procedures are to detect shifts in the process mean vector. In such a case, data in terms of vectors follow p-variate normal distribution with mean vector µ and covariance matrix Σ. Hotelling, H. [1] introduced the Hotelling’s T2 control chart which is used to monitor the multivariate process and its operation is based only on the most recent observation, therefore it is insensitive to detect small and moderate shifts in the mean vector. To overcome this drawback during the last decade, improvement of the Hotelling’s T2 statistic has attracted for the research work.
Wu and Spedding [2] developed the synthetic 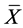 chart as a combination of the Shewhart
chart as a combination of the Shewhart 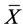 chart and the “Conforming Run Length” (CRL) chart for detecting shifts in the process mean. The CRL chart is an attribute control chart proposed by Bourke [3] for monitoring fraction nonconforming. It was shown that the synthetic
chart and the “Conforming Run Length” (CRL) chart for detecting shifts in the process mean. The CRL chart is an attribute control chart proposed by Bourke [3] for monitoring fraction nonconforming. It was shown that the synthetic  chart outperforms the Shewhart
chart outperforms the Shewhart 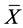 chart over the entire range of shifts in the process mean. The development of the synthetic control chart for a univariate process has been also documented by Calzadaand Scariano [4] , Davis and Woodall [5] , Scariano and Calzada [6] , Huang and Chen [7] , and Costa and Rahim [8] . The development of the Multivariate synthetic control chart for monitoring process Mean vector (MV-Syn-M) has been proposed by Ghute and Shirke [9] . This chart is developed as a combination of the Hotelling’s T2 chart and the CRL chart. The MV-Syn-M chart is an extension of the synthetic chart in multivariate normal data.
chart over the entire range of shifts in the process mean. The development of the synthetic control chart for a univariate process has been also documented by Calzadaand Scariano [4] , Davis and Woodall [5] , Scariano and Calzada [6] , Huang and Chen [7] , and Costa and Rahim [8] . The development of the Multivariate synthetic control chart for monitoring process Mean vector (MV-Syn-M) has been proposed by Ghute and Shirke [9] . This chart is developed as a combination of the Hotelling’s T2 chart and the CRL chart. The MV-Syn-M chart is an extension of the synthetic chart in multivariate normal data.
Purpose of this article is to improve the efficiency of the Hotelling’s T2 chart and the “Multivariate Synthetic control chart to detect shifts in the Mean vector” (MV-Syn-M) by using the recently developed concept of “Group Runs” (GR) and the “Modified Groups Runs” (MGR) control charts. The development of the GR control chart [10] and MGR control chart [11] for univariate process has been documented by Gadre and Rattihalli. We propose the “Multivariate Group Runs control chart for Mean vector” (MV-GR-M) and the “Multivariate Modified Group Runs control chart for Mean vector” (MV-MGR-M) charts, which detect process changes faster than the Hotelling’s T2 chart and the MV-Syn-M chart.
Description of the related multivariate control charts for the mean vector is given in Section 2. Section 3, includes the description and design of the GR and MGR charts. Description of the runs rule representation of the MV-GR-M and MV-MGR-M charts is given in Section 4. In the subsequent section, it is illustrated that in the zero state, MV-GR-M and MV-MGR-M charts outperform as compared to the Hotelling’s T2 chart and the MV-Syn-M chart. We also give one real life situation for the effectiveness of the MV-GR-M and the MV-MGR-M charts. In Section 6, the steady state performances of the MV-GR-M and the MV-MGR-M charts are studied. Concluding remarks are given in the last section.
2. Some Multivariate Control Charts for the Process Mean
This section briefly describes some multivariate control charts to monitor the mean vector of a multivariate normally distributed process namely, Hotelling’s T2 chart and the MV-Syn-M chart.
Let 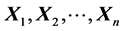 be a random sample from
be a random sample from 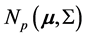 distribution. Here, m is the process mean vector and S is the process covariance matrix. These vectors represent measurements of p quality characteristics. Let
distribution. Here, m is the process mean vector and S is the process covariance matrix. These vectors represent measurements of p quality characteristics. Let 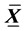 be the sample mean vector of the above sample and m0, S0 be the in control mean vector and covariance matrix respectively. The problem of interest is to detect the shift in the mean vector m. The hypothesis testing problem is equivalent to test the null hypothesis Ho: m = m0 against H1: m ≠ m0. The test statistic for testing Ho against H1 is given by
be the sample mean vector of the above sample and m0, S0 be the in control mean vector and covariance matrix respectively. The problem of interest is to detect the shift in the mean vector m. The hypothesis testing problem is equivalent to test the null hypothesis Ho: m = m0 against H1: m ≠ m0. The test statistic for testing Ho against H1 is given by
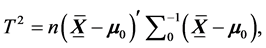 (1)
(1)
2.1. The Hotelling’s T2 Chart
This control chart is used to detect shift in mean vector for the multivariate normal data. The upper control limit is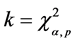 , where
, where 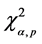 is upper 100α percentage point of chi-square distribution. If the process is in-control, a test statistic T2 is distributed as a chi-square variate with p degrees of freedom, otherwise it follows as a non-central chi-square distribution with a non-centrality parameter l2, where
is upper 100α percentage point of chi-square distribution. If the process is in-control, a test statistic T2 is distributed as a chi-square variate with p degrees of freedom, otherwise it follows as a non-central chi-square distribution with a non-centrality parameter l2, where
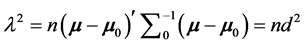
and d denotes a shift of magnitude in the mean vector. ATS for this control chart is
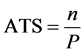 ,
,
where, . The on-target and off-target values of P are
. The on-target and off-target values of P are
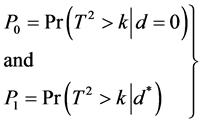 (2)
(2)
where,  is the magnitude considered large enough to seriously impair quality of the products.
is the magnitude considered large enough to seriously impair quality of the products.
Here, we find optimal choices of the two parameters (n, k) for given 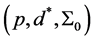 by using “Average Time to Signal” (ATS) model
by using “Average Time to Signal” (ATS) model
 (3)
(3)
2.2. The Multivariate Synthetic Control Chart for Mean Vector (MV-Syn-M)
In MV-Syn-M control chart, for the above problem, Ghute and Shirke [9] computed optimum design parameters (k, L) for given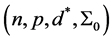 . They obtained optimal choices of the parameters by using ARL model. Further, they have not studied steady state performance for MV-Syn-M control chart. This chart consists of two sub-charts: T2 sub-chart and CRL sub-chart. The operation of this chart is similar to that of the synthetic control chart suggested by Wu and Spedding [2] . Here, we obtain optimal choices of all the three parameters (n, k, L) for given
. They obtained optimal choices of the parameters by using ARL model. Further, they have not studied steady state performance for MV-Syn-M control chart. This chart consists of two sub-charts: T2 sub-chart and CRL sub-chart. The operation of this chart is similar to that of the synthetic control chart suggested by Wu and Spedding [2] . Here, we obtain optimal choices of all the three parameters (n, k, L) for given 

3. Some Group Runs Based Control Charts for the Process Mean
This section briefly describes some group runs based control charts based on ATS criterion, namely the GR chart and the MGR chart. These charts give a significant reduction in out of control ATS as compared to the 
3.1. Group Run Control Chart for Detecting Shifts in the Process Mean
The “Group Runs” (GR) chart proposed by Gadre and Rattihalli [10] which is a combination of the Shewhart’s 

Some notations for the GR chart
1) δ: Design shift in the process mean.
2) ATS(δ): The average number of units required by the time the process has gone out of control.
3) δ1: Design shift in the mean, the magnitude of which is considered large enough to seriously impair the quality of the product.
4) Lg: Lower control limit of GR Chart.
5) τ: The minimum required value of ATS(0).
Operation of the GR chart
Stepwise procedure of operation of the GR chart is as follows.
Step-1: Inspect n units in a group.
Step-2: Declare the group as conforming or nonconforming using 
Step-3: A process is said to be out of control, if either 
Step-4: When the process goes out control, necessary corrective action should be taken to reset and to resume it. Once the process restarts, move to Step-1, before initializing CRL to 0.
Design of the GR Chart
In the synthetic control chart, for the same problem, Wu and Spedding computed optimal design parameters (k, Lg) for the given sample size (n). In case of the GR chart, optimum choices of the three parameters 
Let P be the probability of the group being nonconforming. It is given by,

Here 



3.2. Modified Group Runs Control Chart for Process Mean
“Modified Group Runs” (MGR) chart is proposed by Gadre and Rattihalli [11] . This chart outperforms the Shewhart’s 





Group runs based procedure: The group runs based procedure declares the process as out of control, if 



In case of MGR chart to detect shifts in the process mean, let ATS(δ) be the average number of units required by MGR chart to detect a shift in the process mean from 




4. Multivariate Group Runs Based Control Charts for the Process Mean
In this section, we propose two multivariate group runs based control charts for monitoring the process mean using the Hotelling’s T2 statistic, namely the MV-GR-M chart and the MV-MGR-M chart.
4.1. The MV-GR-M Chart
Some Notations for the MV-GR-M Chart
1) T2 = Hotelling’s T2 statistic
2) Lg = “Lower Control Limit” (LCL) of the MV-GR-M chart.
3) kg = “Upper Control Limit” (UCL) for the status of a group of the MV-GR-M chart.
Implementation of MV-GR-M Chart
Stepwise procedure for the implementation of the MV-GR-M chart is as follows:
Step-1 Inspect n units in succession.
Step-2 Declare the group as conforming or non-conforming through the Hotelling’s T2 statistic. The group is classified as non-conforming when T2 falls beyond kg.
Step-3 A process is said to be out of control, if either 

Step-4 When the process goes out-of-control, the corrective action be taken. Once the process restarts, return to Step-1 before initializing CRL to zero.
In Shewhart type control chart, the zero state and steady state ARL performances are exactly same. However, for the group runs based control charts, the zero state and the steady state ATS performance are not same. We carry out the steady state ATS performance by using the optimal design parameters from the zero state ATS model.
Gadre and Rattihalli [10] obtained the zero-state

4.2. The MV-MGR-M Chart
We applied the MGR technique suggested by Gadre and Rattihalli [11] to develop the MV-MGR-M control chart to detect shifts in the process mean vector. For MV-MGR-M chart, we obtain the design parameters (n, kmg, L1, L2) for given input parameters 
5. Numerical Examples and Comparison in the Zero State
To compare the ATS performance of the MV-GR-M chart and the MV-MGR-M chart with the Hotelling’s T2 chart, T2-syn chart, we consider the sets of input parameters (d, τ), in the zero state case. A macro in MAT-LAB is developed to obtain the design parameters of the MV-GR-M chart and MV-MGR-M chart for given input parameters.
Examples Related to the MV-GR-M and MV-MGR-M Charts and Its Performance in the Zero State
Example1: The input parameters 

τ: 2000 5000 10,000
Considering all possible 18 combination of the input parameters

For multivariate normal situation, since these 18 cases cover almost all the practical si- tuations, we conclude that 



In the zero state, computations indicate that the MV-MGR-M chart is superior in detecting shifts in the process mean vector as compared to the other two compatible MV-Syn-M chart and MV-GR-M chart.
This example shows that, not only 
Normalized ATS (normalized with respect to the MV-Syn-M chart) values are computed for 

It is observed that for d ≥ 0.285, we have ATS(d)mg < ATS(d)g < ATS(d)s< ATS(d)HOT. Thus, the MV-MGR-M chart detects a shift of any size in the multivariate normal processes, for monitoring the process mean vector earlier than the MV-HOT, MV-Syn-M
Table 1. Optimal design parameters and ATS(d) values of the three charts.
Table 2. Normalised ATS values for four control charts for various values of d.
Figure 1. A graph of normalised ATS against C2 values.
and MV-GR-M charts, though optimum values of the design parameters are calculated for a specific d value.
It is to be noted that the run length based charts are not having single initial state. Therefore, it is necessary to study their performance in steady state and should be compared with that of the compatible charts. In the following section we study such performance of the MV-GR-M and MV-MGR-M charts.
A real life example
This example is given to illustrate the use of the proposed chart and compare it to the available Hotelling’s T2 and MV-Syn-M control charts. The data set is collected by the students of M.Sc. Statistics for their project. The data are from most important part, caliper of the brake system that measured the Lug-hole CD which is distance from two bottom holes of the caliper (X1) with the specification 142.05 ± 0.75 mm and diameter which is the distance of center hole (X2) with the specification of 51.07 ± 0.15 mm for 20 samples each size 10. According to historical information about this type of Caliper, the in-control mean vector and covariance matrix were taken as:
Assuming that the in-control process has a 

We compute optimal design parameters for the three control charts for n = 10, p = 2 and α = 0.05, by choosing 
Here, MV-Syn-M, MV-GR-M and MV-MGR-M control charts give an out-of-con- trol signal at sample 10, 7 and 7 respectively. This example illustrates the effectiveness of the MV-GR-M chart and MV-MGR-M chart, compared with the MV-Syn-M chart, for detecting a change of the process mean vector.
Table 3. T2 values for the illustrative example.
Table 4. Optimal design parameters of various control charts.
6. Steady State Behavior of the Various Charts
Davis and Woodall [5] , proposed runs rule for the synthetic control chart for the steady state performance. Gadre and Rattihalli [10] considered the steady state performance of the group runs control chart for detecting shifts in the process mean. Also, Gadre and Rattihalli [11] considered the steady state performance of the MGR control charts to detect increases in fraction non-conforming and shifts in the process mean. Here, we use the same runs rule for the MV-GR-M and MV-MGR-M charts.
It is to be noted that for any run length based control chart, the steady state ATS is not smaller than the zero state ATS. If the signal depends on one point only, both ATSs are the same. The performances of any two charts should be compared by making the (SSATS)0 of the two charts the same. Hence, we compute the adjusted steady state ATS of chart II with respect to the chart I as

The Steady State Performance of MV-GR-M and MV-MGR-M Charts
Example-1 (Cont.): The following table gives the adjusted steady state ATS values corresponding to the values of din Example-1, for all three charts.
From Table 5, we observe the following:
For d ≥ 0.3, (Adj. SSATS)Hot-T2 > (Adj. SSATS)MV-Syn-M > (Adj. SSATS)MV-GR-M
The computations indicate that for shifts (d ≥ 0.3) in the process level, the MV-GR-M chart is superior in detecting the significant shifts compare to the other two compatible Hotelling’s T2 and MV-Syn-M charts in the steady state case.
From Table 6, we observe the following:
For d ≥ 0.4, (Adj. SSATS)MV-Syn-M > (Adj. SSATS)MV-GR-M > (Adj. SSATS)MV-MGR-M
Table 5. SSATS and Adj. SSATS for the hotelling’s T2, MV-Syn-M chart and MV-GR-M chart.
Table 6. SSATS and Adj. SSATS for the MV-Syn-M chart, MV-GR-M chart and MV-MGR-M.
The computations indicate that for shifts (d ≥ 0.4) in the process level, the MV-MGR-M chart is superior in detecting shifts compared to the other two compatible MV-Syn-M and MV-GR-M charts in the steady state case.
7. Conclusion
The MV-GR-M and MV-MGR-M control charts have been developed for the multivariate normal processes, for monitoring the process mean vector. The ATS comparison of the MV-Syn-M chart and the MV-GR-M and MV-MGR-M charts are carried out. The comparison indicates, in the zero state as well as in the steady state, the MV-GR-M and MV-MGR-M charts outperform the chart MV-Syn-M for all the shifts considered.
Acknowledgements
The authors would like to acknowledge Ms. Sanap S. S. and Ms. Sawant V. S., Students of M.Sc. (Statistics), SPPU, Pune for providing relevant data collected for their project.
Cite this paper
Gadre, M.P. and Kakade, V.C. (2016) Some Group Runs Based Multivariate Control Charts for Monitoring the Process Mean Vector. Open Journal of Statistics, 6, 1098-1109. http://dx.doi.org/10.4236/ojs.2016.66089
References
- 1. Hotelling, H. (1947) Multivariate Quality Control Illustrated by Air Testing of Sample Bombsights. In: Eisenhart, C., Hastay, M.W. and Wallis, W.A., Eds., Techniques of Statistical Analysis, McGraw Hill, New York, 111-184.
- 2. Wu, Z. and Spedding T.A. (2000) A Synthetic Control Chart for Detecting Small Shifts in the Process Mean. Journal of Quality Technology, 32, 32-38.
- 3. Bourke, P.D. (1991) Detecting a Shift in Fraction Nonconforming Using Run-Length Control Charts with 100% Inspection. Journal of Quality Technology, 23, 225-238.
- 4. Calzada, M.E. and Scariano, S.M. (2001) The Robustness of the Synthetic Control Chart to Non-Normality. Communication in Statistics-Simulation and Computation, 30, 311-326.
- 5. Davis, R.B. and Woodall, W.H. (2002) Evaluating and Improving the Synthetic Control Chart. Journal of Quality Technology, 34, 63-69.
- 6. Scariano, S.M. and Calzada, M.E. (2003) A Note on the Lower-Sided Synthetic Chart for Exponentials. Quality Engineering, 15, 677-680.
https://doi.org/10.1081/QEN-120018399 - 7. Chen, F.L. and Huang, H.J. (2005) A Synthetic Control Chart for Monitoring Process Dispersion with Sample Range. International Journal Advance Manufacturing Technology, 26, 842-851.
https://doi.org/10.1007/s00170-003-2010-6 - 8. Costa, A.F.B. and Rahim, M.A. (2006) A Synthetic Control Chart for Monitoring the Mean and Variance. Journal of Quality in Maintenance Engineering, 12, 81-88.
https://doi.org/10.1108/13552510610654556 - 9. Ghute, V.B. and Shirke, D.T. (2008) A Multivariate Synthetic Control Chart for Monitoring Process Mean Vector. Communication in Statistics-Theory and Methods, 37, 2136-2148.
- 10. Gadre, M.P. and Rattihalli, R.N. (2004) A Group Runs Control Chart for Detecting Shifts in the Process Mean. Economic Quality Control, 19, 29-43.
- 11. Gadre, M.P. and Rattihalli, R.N. (2006) Modified Group Runs Control Charts to Detect Increases in Fraction Non Conforming and Shifts in the Process Mean. Communication in Statistics-Simulation and Computation, 35, 240.




