Received 20 June 2016; accepted 22 August 2016; published 25 August 2016

ABSTRACT

In this article, to improve the doubly robust estimator, the nonlinear regression models with missing responses are studied. Based on the covariate balancing propensity score (CBPS), estimators for the regression coefficients and the population mean are obtained. It is proved that the proposed estimators are asymptotically normal. In simulation studies, the proposed estimators show improved performance relative to usual augmented inverse probability weighted estimators.

Keywords:

Nonlinear Regression Model, Missing at Random, Covariate Balancing Propensity Score, GMM, Augmented Inverse Probability Weighted

1. Introduction

Consider the nonlinear regression model:

(1)

where 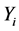is a scalar response variate, 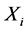is a 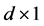vector of covariate, 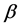is a 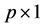vector of unknown regression parameter, 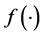is a known function, and it is nonlinear with respect to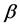, 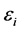is a random statistical error with. In general, d is different from p. The model has been studied by many authors, such as Jennrich [1] , Wu [2] , Crainceanu and Ruppert [3] and so on.

Missing data is frequently encountered in statistical studies, and ignoring it could lead to biased estimation and misleading conclusions. Inverse probability weighting (Horvitz and Thompson [4] ) and imputation are two main methods for dealing with missing data. Since Scharfstein et al. [5] noted that the augmented inverse probability weighted (AIPW) estimator in Robins et al. [6] was double-robust, authors have proposed many estimators with the double-robust property, see Tan [7] , Kang and Schafer [8] , Cao et al. [9] . The estimator is doubly robust in the sense that consistent estimation can be obtained if either the outcome regression model or the propensity score model is correctly specified. The AIPW estimators have been advocated for routine use (Bang and Robins [10] ). For model (1), in the absence of missing data, the weighted least squares estimator of

can be obtained by minimizing the objective function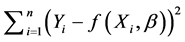. In the presence of missing

data, the above-mentioned method can not be used directly, so we make use of AIPW method to consider the model (1).

Throughout this paper, we assume that X’s are observed completely, Y is missing at random (Rubin [11] ). Thus, the data actually observed are independent and identically distributed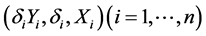, where 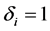indicates that 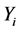is observed and indicates that is missing. The missing at random (MAR) assumption implies that and Y are conditionally independent given X, that is, . This probability is called the propensity score (Rosenbaum and Rubin [12] ).

If, model (1) is just the classical linear model. The linear models with missing data have been studied in existing papers, such as Wang and Rao ( [13] [14] ), Xue [15] , Qin and Lei [16] and so on. The inverse probability weighted imputation methods of Xue [15] and other papers are based on the nonparametric estimators of the propensity score model. However, it is difficult to obtain the nonparametric estimators because of the “curse of dimensionality”, and as mentioned in the Kang and Schafer [8] , the AIPW estimators can be severely biased when both models are misspecified. In addition, there is little work done for model (1) with missing responses.

In this paper, we construct estimators for and of model (1), based on the covariate balancing propensity score (CBPS) method proposed by Imai and Ratkovic [17] . As mentioned in Imai and Ratkovic [18] , the weights based on CBPS are robust in the sense that they improve covariate balance even when propensity score model is misspecified. Our estimator has the following merits: 1) it avoids the “curse of dimensionality”; 2) it avoids selecting the optimal bandwidth; 3) it improves performance of the AIPW estimators in terms of bias, standard deviation (SD) and mean-squared error (MSE), even when both outcome regression model and propensity score model are misspecified.

The rest of this paper is organized as follows. In Section 2, based on the CBPS and the AIPW methods, the estimators for the regression parameter and the population mean are proposed, and the asymptotic properties of the estimators are investigated. In Section 3, simulation studies are carried out to assess the performance of the proposed method. In Section 4, concluding remarks are made. In Appendix, the proofs of the main results are given.

2. Construction of Estimators

The most popular choice of is a logistic regression function (Qin and Zhang [19] ). We make the same choice and posit a logistic regression model for

(2)

where is d-dimensional unknown column vector parameter.

2.1. CBPS-Based Estimator for the Propensity Score

Based on, people can obtain the estimator by maximizing the log-likelihood function:

(3)

Assuming that is twice continuously differentiable with respect to, so maximizing the (3) implies the first-order condition

(4)

where. However, the main drawback of this standard method is that the propensity score model may be misspecified, yielding biased estimators for the interesting parameters, such as and. To overcome the drawback, we borrow the following ideas of Imai and Ratkovic [17] . Similar to arguments present by Imai and Ratkovic [17] , we operationalize the covariate balancing property by using inverse propensity score weighting

(5)

Equation (5) ensures that the first moment of each covariate is banlanced and the weights based on CBPS are robust even when propensity score model is misspecified. The key idea behind the CBPS is that propensity score model determines the missing mechanism and covariate balancing weights, see Imai and Ratkovic [17] . The sample analogue of the covariate balancing moment condition given in Equation (5) is

(6)

According to Imai and Ratkovic [17] , the CBPS is said to be just identified when the number of moment conditions equals that of parameters. If we use the covariate balancing conditions given in Equation (6) alone, the CBPS is just-identified. If we combine Equation (6) with the score condition given in Equation (4), then the CBPS is overidentified because the number of moment conditions exceeds that of parameters.

Combining Equation (6) with the score condition given in Equation (4), we obtain the following equation:

(7)

Let be the solution to the Equation (7). For the overidentified CBPS, the GMM (Hansen [20] ) estimator can be obtained by minimizing the following equation with respect to for some positive-semidefinite symmetric weight matrix W:

(8)

It is easy to show that, under some regularity conditions, is a consistent estimator of, the true value of. For the just-identified CBPS, we borrow the ideas of Imai and Ratkovic [17] and still minimize Equation (8) without the score condition to find.

Theorem 1. Suppose that be a set of independent and identically distributed random vectors, under the Assumptions (A1)-(A3) in the Appendix, then and, where minimizes Equation (8).

2.2. Estimator for the Regression Parameter

To make use of AIPW method, we borrow the idea of Seber and Wild [21] and define the least squares estimator of based on complete-case data by solving the following estimating equation:

(9)

where. There is no closed form of, but it can be obtained by the following iterative equation:

(10)

where and are eval-

uated at. If, where c is a prespecified tolerance and denotes the norm, then

we stop the above iterative algorithm and obtain the least squares estimator of, denoted by.

Although the implementation of the complete case method is simple, it may result in misleading conclusion by simply excluding the missing data. In this section, we introduce an AIPW method based on CBPS to deal with the problems of complete case method.

Denote, From Equation (1), we have

under the MAR condition. Hence

(11)

where’s satisfy. Formula (11) is a full data model without missing data. So similar to Equation (10), we can obtain an estimator of by iterative equation

where with

and is obtained by CBPS method.

The following Theorem 2 gives the asymptotic normality of.

Theorem 2. Suppose that Assumptions (A1)-(A4) in the Appendix hold. Then we have

where, and with.

To apply Theorem 2 to construct the confidence region of, we use to consistently estimate B. where and are defined by

Therefore, we have

(12)

and

(13)

We can construct the confidence interval of using (12) and (13).

2.3. Estimator for the Response Mean

It is of interest to estimate the mean of Y, say, when there are missing data in the responses. We here make use of the method of Xue [15] to construct the estimators of. Let

Under the MAR condition, we have if is the true parameter. Then the proposed estimator is

(14)

In the following theorem, we state the asymptotic properties of.

Theorem 3. Under the assumptions (A1)-(A4) in the Appendix, we have

where with.

Borrowing the method of Xue [15] , we can obtain the following consistent estimator of V:

where

By Theorem 3, the normal approximation based confidence interval of with confidence level is

.

3. Simulation Examples

We conducted simulation studies to examine the performance of the proposed estimation methods. The simulated data are generated from the model with. The components of are generated from the uniform distribution respectively and is generated from the standard normal distribution, is generated from Bernoulli with true propensity score model.

When both models are misspecified or either of them is misspecified, we adopt the same way as Kang and Schafer [8] to examine whether our method can improve the empirical performance of doubly robust estimators

or not. Similar to Kang and Schafer [8] , only the

are observed. If Y is expressed as or propensity score model is expressed as, the model is misspecified. As in the original study, we conduct simulations for population mean under four scenarios:

1) both outcome and propensity score models are correctly specified;

2) only the propensity score model is correct;

3) only the outcome model is correct;

4) both outcome and propensity score models are correctly misspecified.

Due to the regression parameter is in the outcome regression model, we only conduct simulations for under (1) and (3) scenarios. For each scenario, we conduct 1000 simulations and calculate the bias, standard deviation (SD) and mean-squared error (MSE) for and. The results of our simulations are presented in Tables 1-3. For a given scenario, we examine the performance of estimators on the basis of four different propensity score methods:

Remark: 1) Both models are correct; 2) Only propensity score model is correct; 3) Only outcome model is correct; 4) Both models are incorrect.

a) usual GLM method;

b) the just-identified CBPS estimation with the covariate balancing moment conditions and without the score condition (CBPS1);

c) the overidentified CBPS estimation with both the covariate balancing and score conditions (CBPS2);

d) The true propensity score model which we do not need to estimate (TRUE).

From Table 1 and Table 2, we can see that SD and MSE of our estimators for decrease as n increases. Whether the propensity score model is specified correctly or not, the proposed estimators based on CBPS have smaller SD and MSE than the usual GLM estimators mostly. The CBPS with or without the score condition can substantially improve the performance of usual estimator. Compared with estimators based on true propensity score model, our proposed estimators perform as well as them in the terms of SD and MSE. Table 3 shows that, under the four scenarios, the SD and MSE of our proposed estimators remain lower than the usual GLM estimators. Similar to Imai and Ratkovic [17] , the final scenario illustrates the most important point made by Kang and Schafer [8] that doubly robust estimator can deteriorate when both the outcome and the propensity models are misspecified. Under this scenario, the doubly robust estimators based on usual GLM have a significant amount of bias and variance. However, the CBPS can improve the performance of doubly robust estimators. In a word, we obtain the same conclusion as Imai and Ratkovic [17] that the CBPS can yield robust estimators of population mean, even when both the outcome and propensity score models are misspecified.

4. Concluding Remarks

We have proposed an improved estimation method for the parameters of interest in the nonlinear regression model with missing responses. The estimators based on CBPS and AIPW method have the following merits: 1) They avoid the “curse of dimensionality” and avoid selecting the optimal bandwidth; 2) When either the outcome regression model or the propensity score model is correctly specified, the proposed estimators perform as well as estimators based on true propensity model in the terms of SD and MSE; 3) When both outcome regression and propensity score models are misspecified, as mentioned in Section 1, the usual AIPW estimator can be severely biased, but our method improves the performance of them and obtains an improved estimator for population mean. The simulation shows that the proposed method is feasible. Furthermore, with appropriately modification, the proposed method can be extended to other models with missing responses. The exhaustive procedure will be presented in our future work.

Acknowledgements

We thank the Editor and the referee for their helpful comments that largely improve the presentation of the paper.

Cite this paper

Donglin Guo,Liugen Xue,Haiqing Chen, (2016) CBPS-Based Inference in Nonlinear Regression Models with Missing Data. Open Journal of Statistics,06,675-684. doi: 10.4236/ojs.2016.64057

References

Appendix: Proofs of the Main Results

Throughout, let be the true value of, and be the Euclidean norm for a matrix

. Firstly we make the following assumptions.

(A1) For all X’s, is a known, differentiable function from to (0,1) for all a’s in a neighborhood of.

(A2) and exist and the matrix is of full rank.

(A3) 1) W is positive semi-definite and only if. 2), which is compact.

3) and, where.

(A4) and.

To complete the proofs of Theorems 1-3, the following lemma is needed. If there is a function such that 1) is uniquely minimized at; 2) is compact; 3) is continuous; 4) con- verges uniformly in probability to, then, where minimizes subject to.

Lemma 1. is the fundamental consistency result for extremum estimators. Its proof can be found in Newey and McFadden [22] , and we omit it here.

Proof of Theorem 1. Similar to Theorem 2.6 in Newey and McFadden [22] , the proof of is proceed by verifying the conditions of Lemma 1. Under assumption (A2), (A3) and Lemma 2.3 in Newey and McFadden (1994), we know that conditions 1) and 2) hold in Lemma 1. Let

, Under assumption (A1) and by Lemma 2.4 in Newey and

McFadden (1994), we have and is continuous. Thus, condition 3 in

Lemma 1 holds by continuous. By is compact, is bounded on, and by the Cauchy-Schwartz inequalities, , and condition 4) in Lemma 1 holds. According to Theorem 3.2 in Newey and McFadden [22] , we can obtain that.

Proof of Theorem 2. Denote, where. By the definition of,

(15)

To prove Theorem 2, we will verify the asymptotically normality of. By direct calculation,

we have

(16)

where

(17)

Under MAR assumption, we have. This combines with Theorem 1

yields

(18)

From the Theorem 5 in Wu (1981), we know that. This together with (16) and (18) proves that

(19)

By Theorem 1,

According to the assumptions given in model (1), we have

Then, it follows from the central limit theorem that

Therefore, by using (19) and Slutsky theorem, the proof of Theorem 2 is completed.

Proof of Theorem 3. By direct calculation, we have we have

(20)

where

By the central theorem, we have. To prove the asymptotically normality of estimator, we need to prove that. For,

Similar to arguments of Qin and Lei [16] , we have.

For, Under MAR assumption, we have. Therefore,

. This combines with Theorem 1 and yields

. Then the Theorem 3 is proved.

NOTES

^*Corresponding author.