Received 10 March 2016; accepted 24 April 2016; published 27 April 2016

ABSTRACT

The extraction of various reserves is one of the most important measures that guarantee insurance companies’ solvency. Accurate assessment of non-life insurance claim reserves needs to consider the volatility risks of inflation. This paper presents a stochastic model of claim reserves including inflation factor and diagonal effects. By applying this model, we can predict the values of the claim reserves and evaluate predicting risks. Through analyzing actual data and using the bootstrap method, we can compare Bornhuetter-Ferguson method involving diagonal effects with chain ladder method. It is shown that the former is more efficient and robust than the latter.

Keywords:

Claim Reserves, Diagonal Effects, Bornhuetter-Ferguson Method, Chain Ladder Method, Inflation, Bootstrap

1. Introduction

In insurance industries, inflation can be divided into two categories: economic inflation and claim inflation. The latter’s impact on claim reserves estimations is more complicated than the former. In actuarial literature, there are few studies on the inflation’s impacts on claim reserves estimations. Economic inflation can be quantified by CPI, etc. However, it is difficult to estimate the fluctuations risk on prediction of claim reserves resulting from claims inflation.

It is pointed out in David [1] that in calculation of the loss reserve variance, inflation index should be extracted theoretically from insurance loss data itself, but actual insurance data are not stable enough to provide a credible evaluation; therefore, external factors should be applied to characterize the inflation index.

A model with diagonal effects depicting the effects of economic inflation was established in Rietdorf [2] of the form,

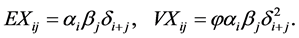
It should be noted that diagonal effects 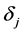come from two aspects: one is economic inflation expressed as a relevant price index which implies that claim payments are related to the calendar time; the other is the claims inflation. This factor, generally speaking, comes from legal issues and the compensation way.

In Kuang [3] [4] the claim inflation is assumed to satisfy,

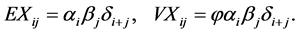
We cannot tell whether the economic inflations or the claims inflation lead to the changes along the diagonal, just from diagonal, just from the run-off triangle. To solve this problem, two different models are proposed in Jessen and Rietdorf [5] . Let 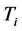take places of, where 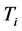is considered known; we can reduce the number of unknown parameters in above models and derive the unique solutions. Further, through the following models we can determine the value of parameter c. When c = 0 the change is caused by claim inflation; when c = 1 the change is caused by economic inflation; other cases are caused by both.

A Bornhuetter-Ferguson type method including diagonal effects is given by,

where the exposure parameters 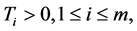and 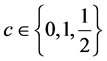are assumed to be known.

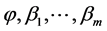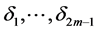and are positive unknown constants which satisfy

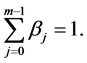
A credibility model including diagonal effects is given by,

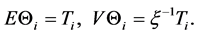
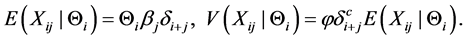
They choose 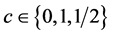for reasons: c = 0 corresponds to claims inflation; c = 1 corresponds to economic inflation; c = 1/2 is chosen in a situation where both effects have an impact on data.

However the specific choice of c is based on intuition as well as plots of residuals which contain so much randomness and the range of value c is not accurate enough.

This paper uses the model structure similar to the one in Jesson and Rietdorf [5] (a Bornhuetter-Ferguson method including diagonal effects). The differences lie in our model which expands the value of c on {0; 1/4; 1/2; 3/4; 1} and changes the method of choosing c. Instead of checking the residuals plots for each c, we take the c under which the coefficient of variation is minimum of yearly claims reserving.

The reason why we change the method of choosing c is actually the plotted points for each c are almost the same. All the residuals can be taken as independent identically distributed. What’s more, coefficient of variation and standard deviation of reserve estimators are important indicators to evaluate estimators’ accuracy.

This article uses VBA to analyze actual data and simulate estimators’ statistical characteristics. The results show that by applying bootstrap method, Bornhuetter-Ferguson method with diagonal effects is more effective and efficient than chain ladder method when predicting claim reserves.

2. Extended Bornhuetter-Ferguson Model including Diagonal Effects

Let be the observable incremental claims, which occurs in accident year i and development year j. Denote

where

Let be the set of natural numbers, be the set of positive integers and m the calendar year. Write

With data we can make predictions of which are unobservable random variables at time m. We can see the detail in Figure 1.

As a technical basis for prediction we consider a model for. The model requires are mutually independent and satisfy the condition:

(1)

(2)

where are row effects which will be represented by yearly exposure measures. are the exogenous indexes which related to inflation. and are positive unknown constants. Satisfy,

(3)

The value of c quantifies claims inflation and economic inflation’s effect on claims reserving estimation,

is assumed to be known.

c = 0 corresponds to claims inflation; c = 1 corresponds to economic inflation; c = 1/4, 1/2, 3/4 corresponds to the ratio of the effects of claims inflation and economic inflation on claims reserving estimation.

3. Solving Proportionality Value β_i and Estimating Exogenous Index δ_i+j

3.1. Separation Method

We can know from Taylor [6] that if we assume the conditions affecting individual claim sizes remained constant, then the ratios of average claim amount paid in development year k per claim with year of origin i would have an expected value which is independent of i. With further assumption if claims cost of a particular development year is proportional to some indexes which relate to the year of payment rather than the year of origin, the expected claims cost of development year j per claim with year of origin i is where is exogen-

ous index appropriate to year of payment k satisfy These expected values then form the following

run-off triangle.

The corresponding value in triangle denoted by observed values where = number of claims

settled in development year o + estimated number of claims outstanding at end of development year o (both in respect of year of origin i). From Figure 2 we can derive the following results.

Sum along the diagonal involving, obtain

Thus estimate of is. Sum along the next diagonal, the result is

is the sum of the column of the triangle involving. So

Now,

This procedure can be repeated, leading to the general solution:

where is the sum along the (h + 1)-th diagonal and is the sum down the (k + 1)-th column.

From (1) we have let replaces, replaces, replaces. We

can solve out and.

3.2. Total Marginal Principal

In classification system, it requires the sum of pure insurance cost is equal to the sum of the corresponding experience compensation cost under different level of classification variables, i.e., the marginal sum of estimations equals to the marginal sum of observations.

Make a transformation. Then is in the form of,

Based on total marginal principal we can derive that,

Put, then

Finally

(4)

(5)

3.3. Consistency of Parameters’ Estimation

In this section we will prove the consistency of. Give the proposition as following

Proposition 3.3. If for all then, for

Proof. Make a transformation of we attain,

Apply Chebyshev’s inequality, if we have,

Namely Use recursive schemes (3)-(5) with the continuous mapping theorem we acquire the desired result.

3.4. Prediction of Diagonal Effects

In this subsection we predict diagonal effects.

We assume obey an AR (1) process, that is,

By means of least-squares method we acquire the least square estimation of,

(6)

Then the predictors of are in the form of

(7)

As a result are predicted by

(8)

4. Solving Method of φ, c

In this section we try to estimate and determine parameter c by considering the residuals, Define variance structure

(9)

Apply the second moment method, can be estimated by Together with (2), we can derive.

Combined (8) with (1), we can yield estimation of

. (10)

The next step in the estimation procedure is to apply the bootstrap method similar to the one in England and Verrall [7] . It should be noticed the bootstrap method is based on the assumption that the residuals are Independent Identically Distributed. By random sampling with replacement we attain.

Finally, we generate Independent Identically Distributed versions of by

(11)

To determine parameter c, for each we plot points to check which

residual plots give the best fit to Independent Identically Distributed. Meanwhile, with all parameters being

solved we can use (8) and to estimate yearly reserve and calculate its standard

deviations, variance coefficient. Through above two points we could make the final choice of value c.

5. Empirical Analysis

Our data is from Jesson and Riedorf [5] which contains 13 years run-off for a portfolio of third-party liability for auto insurance. The data is shown in incremental form in Table 1.

In the model we assume that row effects are known and represented by yearly exposure measures given in Table 2.

The estimators of the parameters are shown in Table 3.

Now, we should predict

Firstly, take unit root/stationarity test to the result is given in Table 4.

Obviously we cannot refuse null hypothesis: z has a unit root.

Secondly, get 1^st differences of z and take unit root test. The result is given in Table 5.

^*MacKinnon (1996) one-sided p-values.

Then we can generate ACF and PACF plots for dz. Autocorrelation and Partial Correlation are shown in Figure 3.

Let be a mean zero white noise process. From Figure 3 we have

Finally we take Dicky-Fuller Test of given in Table 6.

Though R-squared < 0, the value of coefficient approximates to 1. What’s more, we need to take estimation error of into consideration and construct a simple easy-to-implement model. Above all we can assume

^*MacKinnon (1996) one-sided p-values.

obey an AR (1) process. Using Equations (6) and (7) in Section 3.4, we can get

.

Further, if we make the assumption that.

For each c = 0, 1/4, 1/2, 3/4, 1, we plot points and take runs test to verified stochastic feature by the SPSS. Whether c = 0, 1/4, 1/2, 3/4, 1, the p-value = 0.753 > 0.05, the residual error is mutual independent. What’s more, the residual plots seem little difference. Then we compared the statistical characteristic parameters of reserve estimators finding in the case c = 0 the standard deviations, variance coefficient of yearly reserve estimates is minimal.

Naturally apply, we can derive c = 0,.

Finally we generate identically distributed versions of as following:

For each k we can use (7) and the notation to predict yearly reserve estimators.

Let k = 50000, take the average of 50000 times’ claims reserve predictors as each year’s claims reserve estimates. We use excel VBA to realize the procedure.

Table 7 and Table 8 are reserve estimators and its distribution characteristics which are respectivelyacquired by B-F method including diagonal effects and chain ladder method.

Comparing above results, we could find that applying bootstrap method on extended Bornhuetter-Ferguson model including diagonal effects is more conservative than chain ladder method to predict claims reserve.

We produce a histogram for the total reserve by extended B-F model in Figure 4. In Figure 5 we give reserve estimator’s standard deviations with two methods.

We could find that Bornhuetter-Ferguson method including diagonal effects’ standard deviation is smaller in general than chain-ladder method except the total reserve estimation. This shows extended Bornhuetter-Fergu- son model including diagonal effect could improve the accuracy of the estimation of claims reserve.

6. Conclusion

This paper introduces extended Bornhuetter-Ferguson model which is more accurate on estimating claim reserves than Bornhuetter-Ferguson model when considering inflation. Having comparing with the traditional chain-ladder method, we could conclude that it prefers to the extended Bornhuetter-Ferguson model when the inflation is mainly caused by claims inflation. Lacking of insurance data we cannot verify conclusion by national data. It is necessary to further study the case that the fluctuations risk of claim reserves is caused by economic inflation or the mix of economic and claims inflation. We can also take the Bayes method into consideration in the case which claims that priori estimate is not dependability enough.

Cite this paper

Ting Yan, (2016) The Prediction of Non-Life Claim Reserves under Inflation
—An Analysis including Diagonal Effects. Open Journal of Statistics,06,320-330. doi: 10.4236/ojs.2016.62028

References