Open Journal of Statistics
Vol.06 No.03(2016), Article ID:67595,32 pages
10.4236/ojs.2016.63043
Spatial Modeling and Mapping of Tuberculosis Using Bayesian Hierarchical Approaches
Abdul-Karim Iddrisu1, Yaw Ampem Amoako2
1Department of Statistical Sciences, University of Cape Town, Cape Town, South Africa
2Department of Medicine, Komfo Anokye Teaching Hospital, Kumasi, Ghana
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 February 2016; accepted 19 June 2016; published 22 June 2016
ABSTRACT
Global spread of infectious disease threatens the well-being of human, domestic, and wildlife health. A proper understanding of global distribution of these diseases is an important part of disease management and policy making. However, data are subject to complexities by heterogeneity across host classes. The use of frequentist methods in biostatistics and epidemiology is common and is therefore extensively utilized in answering varied research questions. In this paper, we applied the hierarchical Bayesian approach to study the spatial distribution of tuberculosis in Kenya. The focus was to identify best fitting model for modeling TB relative risk in Kenya. The Markov Chain Monte Carlo (MCMC) method via WinBUGS and R packages was used for simulations. The Deviance Information Criterion (DIC) proposed by [1] was used for models comparison and selection. Among the models considered, unstructured heterogeneity model perfumes better in terms of modeling and mapping TB RR in Kenya. Variation in TB risk is observed among Kenya counties and clustering among counties with high TB Relative Risk (RR). HIV prevalence is identified as the dominant determinant of TB. We find clustering and heterogeneity of risk among high rate counties. Although the approaches are less than ideal, we hope that our formulations provide a useful stepping stone in the development of spatial methodology for the statistical analysis of risk from TB in Kenya.
Keywords:
Bayesian Hierarchical, Heterogeneity, Deviance Information Criterion (DIC), Markov Chain Monte Carlo (MCMC), Host Classes, Relative Risk

1. Introduction
The global spread of infectious diseases threatens the well-being of human population as well as that of domestic and wild animals. Therefore, a proper understanding of the pathways and global spread of communicable and infectious diseases is an important aspect of disease management and policy making. However, the data collected with the object of understanding these patterns are subjected to complications brought about by heterogeneity that can be of spatial or non-spatial in nature [2] [3] . Ignoring these complexities is likely to mislead inference which may results in erroneous conclusion [2] [3] . Disease data can be case-event or counts from non-over- lapping regions. Since the data provided for this study only have county level spatial resolution, the approach will be to analyses the data as regional or county specific count data.
There exists a vast amount of literature concerning the development and application of disease mapping approaches [4] - [8] . Spatial distribution of a disease is often understood through application of statistical methods to the data and creating maps that visually describes spatial variation of disease risk [3] . However, disease counts maps are subjected to numerous problems. One such problem is the Modifiable Areal Unit Problem (MAUP), which occurs when inference at the areal level differs from that which is observed at the basic observational unit. This is likely to change conclusions drawn from a study of a count data. The MAUP can be addressed by scaling up to ensure smoothing or averaging of data and making inference at high aggregate level than that used in the analysis. MAUP can also be addressed by scaling down to enable inference at lower level than that used in the analysis. Multi-scale Analysis can also be used to addressed MAUP. This analysis concerns spatial units that are completely matched when aggregated [9] . Also differences in population between regions result in differences in variance of regional estimates. This problem is addressed by employing a hierarchical Bayesian model that smooths the risk from neighboring regions and clearly accounts for population difference by using a Poisson distribution for outcomes.
Bayesian methods are widely used in disease mapping. [10] applied the the Empirical Bayes (EB) methods for smoothing a map of lip cancer rates. They assumed a multivariate normal for the log relative risks and allowed for spatial correlation via conditional autoregressive model. Their model could not be considered to be a “fully Bayesian”, since a quadratic approximation was used for the likelihood and this did not account for the uncertainty in the estimates of the hyper-parameters. [11] was the first example of fully Bayesian disease mapping. They used the convolution prior model described in Section 6.1 to model the log relative risk. They found that the model shrunk extreme disease rates towards the mean and detected spatial association that was apparent in the raw data. According to [11] , the fully Bayesian model produced more accurate estimates than that produced by Clayton and Kaldor approach.
[12] ecological study applied Bayesian hierarchical regression model to evaluate the urban spatial and spatio- temporal distribution of TB in Rilirão Preto, state of São Paulo, Southeast Brazil between 2006-2009 and to evaluate TB risk determinants. The study reveals that TB rates are correlated with measures of income, education and social vulnerability. They state that complex relationship may exist between TB incidence and a wide range of environmental and intrinsic factors, which need to be studied in future research. [13] applied both the Bayesian approach and the generalized mixed model to produce smooth relative risk maps of TB and to model relationship between TB new cases and national TB control program indicators. Their study discovered that high TB risk areas were clustered and TB distribution found to be associated with the number of patients lost to follow-up and the number house holds with more than one case. [14] study on assessing the prevalence of TB in New York from 1970-2000 using Bayesian analysis approach stated that decline in TB incidence could probably be as a result of good control programs and raised in TB prevalence could be attributed to social disruptions such as homelessness, drug abuse, poverty, and overcrowding. Their study confirmed that increase in TB is mainly due to HIV epidemic. [15] study of TB pattern in India, using the Bayesian conditional autore- gressive model revealed that north-eastern states have high risk of TB than other regions.
In this paper our focus is to propose best fitting Hierarchical Bayesian approaches for modeling and mapping relative risk tuberculosis in Kenya. Specifically, we determine suitable spatial and non-spatial models for modeling TB in Kenya.
In Section 2, we describe the data used followed by a Bayesian modeling framework in Section 3. In Section 4, we describe two relative risk detection methods. In Section 5, we described Bayesian non-spatial models and spatial models in Section 6 for disease mapping. We give discussion and conclusion in Section 7.
2. Data Description
The data used in this study is routine data from Kenya Demographic and Health Surveys (DHS). The data contain records of Kenya’s population size, tuberculosis cases, and some suspected determinants of tuberculosis for each period from 2002-2009 and for each 67 districts. To study the risk of TB infection in each county, the data from the 67 districts were aggregated to provide county level summaries. Some of the determinants of TB that were recorded are: HIV prevalence, poverty prevalence, illiteracy, population less then 5 km to health facility, firewood, altitude and mean house hold size. Summary Statistics for these determinants of TB are shown in Table 1.
3. Bayesian Modeling Framework
Bayesian methods define the posterior distribution which is the distribution of the parameter(s) given the observed data. This implies that we require a likelihood function for the observed data and a prior distribution for the unknown parameters. Let  be a random variable with probability density function
be a random variable with probability density function , where
, where 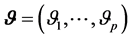 is a vector of relative risk parameters. The likelihood function of
is a vector of relative risk parameters. The likelihood function of  is defined as
is defined as
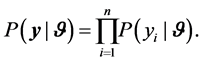 (1)
(1)
Equation (1) is based on the assumption that the sample values of 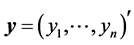 given the parameters
given the parameters 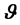 are independent [9] . Once the data model (likelihood function) is chosen, a Bayesian analysis requires the assertion of a prior distribution for the unknown model parameters. The prior distribution can be viewed as representing the current state of knowledge, or current description of uncertainty, about the model parameters prior to data being observed. A prior distribution is a distribution assigned to the parameter
are independent [9] . Once the data model (likelihood function) is chosen, a Bayesian analysis requires the assertion of a prior distribution for the unknown model parameters. The prior distribution can be viewed as representing the current state of knowledge, or current description of uncertainty, about the model parameters prior to data being observed. A prior distribution is a distribution assigned to the parameter 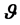 before the data
before the data 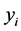 are observed [9] . All parameters within the Bayesian models are stochastic and assigned appropriate prior distribution [9] . Given a single parameter,
are observed [9] . All parameters within the Bayesian models are stochastic and assigned appropriate prior distribution [9] . Given a single parameter, 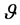 , the the prior distribution is denoted as
, the the prior distribution is denoted as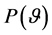 , while for a parameter vector,
, while for a parameter vector, 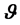 , the joint prior distribution is denoted as
, the joint prior distribution is denoted as .
.
The posterior distribution is a probability distribution of the parameters given the data. The posterior distribution which is proportional to the product of the likelihood function and the prior distribution is defined as
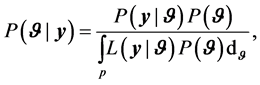 (2)
(2)
where  is called the normalizing constant. It have been shown that posterior distribution of
is called the normalizing constant. It have been shown that posterior distribution of
the parameters (2) can be written as

Table 1. Summary statistics for TB determinants.
from which parameter estimates are drawn using Markov Chain Monte Carlo (MCMC) vis Gibbs sampling [16] . True parameter estimates are obtained when the the Markov chain converges. Convergence diagnostics for each parameter estimate under each implementation is shown.
4. Cluster Detection
This section discusses methods used in disease mapping to detect elevated risk. One such methods is the use of the posterior 




from the posterior sample values 


In evaluating






These measures can be used to detect different forms of clustering [9] . However, the usefulness of the execeedence probability depends on the model that has been fitted to the data and that any poorly fitting model will not demonstrate exceedence relate to clustering [9] .
5. Bayesian Hierarchical Non-Spatial Models for Disease Mapping
This section presents two non-spatial models used in disease modeling and mapping. These are the Poisson- Gamma (PG) and the Poisson Log-Normal (LN) models. These models are often used to model small area count data and are appropriate when there is relatively low count of disease and the target population is relatively large in each small area. We present the PG model first followed by the LN model.
5.1. The Poisson-Gamma Model (PG)
The Poisson-Gamma model for relative risk estimation uses a gamma prior distribution for the relative risk combines with the Poisson likelihood function for the disease counts which gives a gamma posterior distribution for the relative risk. The Poisson-Gamma model is widely used in disease mapping to account for extra variability in the data through the prior distribution [18] .
5.2. Model Description
Suppose that the unknown risk of TB in region i is given as


region i can then be written as

Under the frequentist paradigm, we assume that


and

The maximum likelihood estimator 



This estimator, 






and prior distribution for 

5.3. Parameter Estimation
We used Bayesian hierarchical methods for parameters estimation in the Poisson-Gamma model. That is, if in addition, a and b are given prior distributions such that 





In this paper, we defined 


Parameters estimation of the Poisson-Gamma model was carried out using MCMC via Gibbs Sampling. Convergence of the Chain occurs at 40,000 iterations after a burnin period of 1000 sample and thinning of every 30th element of the sample. Figure 1 presents the MCMC convergence diagnostics plots.
5.4. Markov Chain Monte Carlo Diagnosis
Figure 1 presents Gelman and Rubin convergence diagnostics of the Poisson-Gamma model: Column-wise from the top left, Figures 1(a)-(j) are trace plots for a, b, the mean and variance respectively. Figures 1(b)-(k) are posterior marginal density plots for b, a, the mean and the variance respectively. Figures 1(c)-(l) are auto- correlation plots for b, a, the mean and the variance respectively. The Gelman and Rubin trace plots show the convergence of the two parallel chains (Chains with different initial values). “Vanishing” autocorrelation function (ACF) plots show that there is low correlation among parameters that constitute the chain. More satis- factory kernel density plots for parameters of interest would more bell-shaped or symmetric. The density plots for the parameters show that convergence of the chain has reached.
The posterior statistics of the Poisson-Gamma model are shown in Table 2. Table 2 shows that the mean of
Figure 1. Poisson-gamma model: convergence diagnosis of Markov Chain Monte Carlo.
Table 2. Posterior statistics of the poisson-gamma model.
the posterior relative risk is 0.93 (95% credible interval = 0.82 - 1.08). The posterior mean is approximately the same as the mean of the standardized mortality ratio 0.93 (95% credible interval = 0.62 - 1.05) (Equation (8)). The standard deviation of the relative risk, 0.42 (95% credible interval = 0.35 - 0.56), is lower than the standardized mortality ratio's standard deviation 0.49 (95% credible interval = 0.62 - 1.05). Thus their standard deviation has been reduced by 82% by the Poisson-Gamma model. The significance of the variance indicates variation in risk among counties. In a situation of rare cases, standard deviation of the Poisson-Gamma model is expected to be much lower than that of the standardized mortality ratio [18] .
Figure 2 shows standardized mortality ratio for TB prevalence in the counties of Kenya for 2002-2009. The
Figure 2. Kenya county level standardized mortality ratio’s maps: (a) The mean of the SMR and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
SMRs vary around their mean, 0.93 with standard deviation, 0.49 (as discussed in Table 2). There is some suggestion of high TB prevalence in the North, West, North-West and Central counties of Kenya and low TB prevalence in the South-East counties except Mombasa (SMR > 2.0).
From Figure 3, we observed high risk of TB prevalence in the North, West, North-West and Central counties of Kenya and low risk in the South-East counties except Mombasa. Nairobi and Mombasa have the highest relative risk (RR > 2.0) and Laikipia, Nandi, Narok, Nyamira, and Vihiga have the lowest risk (RR < 0.5). The mean of the posterior relative risk and the SMR are the same. The range of the posterior relative risk of the Poisson-Gamma remains the same as the SMR, each having lowest relative risk estimated at 0.40 and the highest risk at 2.38. Variability in risk remains the same due to abundant of information or data.
The map of the exceedence probability in Figure 4 revealed 13 counties that exhibit high risk of TB above the national risk (RR > 1). These counties are: Nairobi, Mombasa, Kisumu, Turkan, Migori, Homa bay, Uasin
Figure 3. Kenya county level poisson-gamma posterior mean relative risk maps: (a) The mean of the posterior relative risk and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
Gishu, Isiolo, Marsabit, Siaya, Tharaka-Nithi, Mandera, and Embu. This map confirms with Figure 3 concern- ing high and low TB prevalence areas.
Despite the fact that assigning a gamma prior distribution for 
5.4.1. Poisson-Log-Normal Model
We now present a model which allows for flexibility of covariates adjustments or incorporation. [18] noted that in disease mapping, the log-normal model is important as it provides a specification that allows for incorporation of covariates. In section we consider LN model without incorporating random effects and covariates and LN model which takes into account random effects and covariates. The random effect term captures or explains
Figure 4. Poisson-Gamma posterior relative risk exceedence probability map: Row-wise from the top left figure: (a) the posterior mean relative risk exceedence probability and (b) its 3 2.5% quantile for relative risk, (c) median for the relative risk and (d) 97.5% quantile for the relative risk.
heterogeneity in relative risks of TB among counties. The LN mode with the random effect is often refer to as the unstructured heterogeneity (UH) model.
5.4.2 Model Description
Let 











Chain Monte Carlo via Gibbs Sampling. Convergence of the MCMC was reached at 11,000 iteration after a burnin period of 10,000 sample and thinning of every 30th element of the chain. Convergence diagnosis plots are presented in Figure 5 and posterior statistics of parameters are presented in Table 3.
We now consider a Poisson LN model with area-specific random effect or uncorrelated heterogeneity (UH) effect 



where 

residual unexplained log relative risk in region i and 

From Equation (13), we can write the relative risk as
Figure 5. Poisson log-normal model: convergence diagnosis of Markov Chain Monte Carlo.
Table 3. Posterior statistics of Poisson log-normal model without covariate and random effect.

where 


or the overall risk effect. Here, the mean 


5.4.3. Parameter Estimation
Since


We would need the prior distributions for 





We now show that the posterior distribution of 
5.5. The Likelihood Function of a Regression with Gaussian Random Effect
Consider a response random variable

regression function of 


regression density or likelihood function for 

where 

where



standard model:



where 



uation (19), we have

Finding the derivative of Equation (21), it follows that

Solving Equation (22), we have

Now finding the second derivative of Equation (25), we have:

Hence, we can rewrite Equation (22) as

From the Taylor’s expansion in Equation (20), and by the Maximum Likelihood Principle (MLP) that
it follows that

Taking exponent on both side of Equation (26), we have

or

where

5.6. Posterior Function of Gaussian Process Regression
Assuming that the prior distribution of 

Then writing only the terms from the likelihood and prior which depend on the weights, and “completing the squares” for Multiple parameters model, the posterior function is defined as

Simplifying Equation (31), it follows that

where 





Comparing Equation (32) with Equation (33), we have

That is




In fact the MAP is similar to the maximum likelihood value

It follows that the posterior distribution for 

Therefore, the prior distribution of 

and the prior distribution for the area-specific random effect defined by

Therefore, the posterior distribution is defined as

Hence,

The prior distribution for the linear regression coefficients is given by


The Equation (42) is the hyperprior distribution for 




We first consider the LN without covariates. Parameter estimation was carried out using Bayesian Markov Chain Monte Carlo via Gibbs Sampling. MCMC convergence was reached at 100,000 iterations after a burnin period of 10,000 sample and thinning of every 30th element in the sample. Figure 5 presents convergence diagnostics plots of this model. Table 3 presents the Posterior statistics of the LN model.
Table 3, revealed that the overall mean of the posterior relative risk is −0.17 (95% credible interval = (−0.31, −0.046). This indicates that the overall TB risk effect in Kenya estimated by the Poisson Log-Normal model decreases keeping all other determinants of TB constants. The standard deviation of the relative risk is 0.46 (95% credible interval = 0.37 - 0.56) with precision variation 
Figure 6, revealed that TB risk is expected to be high in the North,West, North-West and central counties of
Figure 6. Kenya County level TB prevalence counts: Poisson log-normal model without covariate and random effect. (a) the posterior relative risk map and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
Kenya and low risk in the South-West counties. According to this model, Nairobi and Mombasa are expected to have the highest TB risk (RR > 2.0) and Nandi, Narok, Nyamira, Vihiga, and laikipia are expected to have the lowest TB risk (RR < 0.5). Counties with relative risk above the national risk (RR = 1) are apparent from Figure 7. Again, due to abundant of data or information, the range of the posterior relative risk of the Poisson Log- Normal remains the same to that of the SMR. The lowest estimated risk is 0.40 and highest estimated risk is 2.38. There is no reduction of relative risk range compare to SMR's risk as would be expected in a case of rare information or data.
The exceedence probability map Figure 7 confirmed with the Poisson-Gamma model that 13 counties have their TB risk above the national risk. These counties are: Nairobi, Mombasa, Kisumu, Turkan, Migori, Homa bay, Uasin Gishu, Isiolo, Marsabit, Siaya, Tharaka-Nithi, Mandera, and Embu. Figure 7 confirms with Figure 6 that high risk of TB prevalence is observed in the North, West, North-West and central counties and low risk in the South-East counties except Mombasa.
Figure 7. Kenya County level TB prevalence counts: poisson log-normal model without covariate and random effect. (a) the posterior relative risk exceedence probability map and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
We now present the results of the Poisson log-normal model with with UH and covariates effects. Figure 8 presents the Rubin and Gelman convergence diagnostics plots of this mode. Table 4 revealed that the overall level of relative risk effect estimated is 




Figure 9 also confirmed that out of the 47 counties in Kenya, 13 exhibit TB relative risk higher than the national risk (RR = 1). Table 5 presents counties in groups according to their relative risk level. High TB risk can again be observed that in the North, West, North-West and central counties of Kenya and low TB risk in the South-East counties except Mombasa.
Table 5 presents the results of the UH model with counties categorised according to their range of relative risk. The results showed that 14 counties have their relative risk above 1 and the lowest risk counties are 5. The exceedence probability map in Figure 10 visually presents counties with risk above 1. Figure 10 shows 14 counties having elevated risk of TB. These maps again confirmed high TB risk in the North, West, North-West and central counties of Kenya and low risk in South-East counties of Kenya except Mombasa.
Figure 11 is the maps of the area-specific random effect
Table 4. Posterior statistics of the poisson log-normal model with UH effect.
Table 5. UH results indicating counties with high and low TB risk.
Figure 8. Poisson log-normal model with UH and covariates effects: convergence diagnostics of Markov Chain Monte Carlo.
5.7. Summary of the Non-Spatial Models
Though the Poisson-Gamma model provides good information about the TB prevalence in Kenya, one of its shortcomings is that it is unable to handle problem of spatial correlation and incorporation of covariates [18] . The Poisson Log-Normal model provides specifications that allow for incorporation of covariates. The Poisson Log-Normal model also enable us to capture the area random effect and to explain the extend of risk variability among counties through the unstructured random effect term
Though thinning reduces the speed of the MC but it significantly reduces the number of iterations and solves the issue of autocorrelation among parameters that form the chain. Thinning reduces storage demand while preserving the integrity of the MC process [19] . [19] noted that the value of every 
The slower the chain to converge, the more careful one should be about the burn-in period. However, it should be noted that there is no standard, systematic or guaranteed way of determining the length of the burn-in period [19] . Nevertheless, considerable work on convergence diagnostics has been done to make specific recommendations and identify tests [19] .
HIV is identified as significant among the covariates considered. Reason being that HIV patients have their immune system weakened or destroyed by the HIV rendering the body natural defence incapable of carrying out its function of protecting the body against other diseases. Since HIV has this capacity to weaken the immune system, it also implies that it has the effect of re-activating latent TB to active TB in individuals who are latently infected. Models that allow for handling spatial correlation are discussed in Chapter 6.
Figure 9. Kenya county level TB prevalence counts: UH smooth relative risk map (a) and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
6. Bayesian Hierarchical Spatial Model for Disease Mapping
This section presents spatial models used to identify and detect clustering of disease risk in the study area of interest. Spatial data are directly or indirectly referenced to a location on the surface of the earth. These models would allow for borrowing of strength between neighbouring counties such that neighbouring counties shall have similar risk whiles distant counties are expected to show variation in risk. The idea of spatial auto- correlation in spatial data analysis is that values of variables in near-by locations are more similar or related than those far apart. Waldo Tobler’s first law of spatial analysis states that “everything is related to everything else but near-by things are more related than distant things” [20] . In particular, we investigate the statistical pro- perties of the Conditional Autoregressive (CAR) model and the [11] models.
Figure 10. Kenya county level TB prevalence counts: UH smooth relative risk exceedence probability map (a) and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
6.1. Conditional Autoregressive (CAR) Model
Though conditional autoregressive models where introduced decades ago by [11] , they were not widely used until the 1990s. Since they are defined conditionally, they are particularly suited for use with the Gibbs sampler [21] . The Conditional Autoregressive (CAR) models have been used extensively to identify and detect clustering in diseases risk. In these models, risks of disease at any given area is affected by the risk in the neighbouring areas. These models have been referred to as the structured model or the Correlated Heterogeneity (CH) models. That is, estimation of risk in any given area depends on risk at neighbouring areas [18] . The distances or boundaries between the regions are often used in determine neighbourhood properties within CAR models [22] .
Generally, the CAR model is a continuous Markov random field with a conditional probability density function characterization and designed to model spatial phenomena that are highly related to a specific local context [23] [24] . Application of CAR models can found in [23] [15] [25] . Let 
Figure 11. Area-specific random effect: the posterior map (a) and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
area to be studied. Let 



In the Gaussian CAR model, we often assume that each observation of the outcome variable 

These are full conditionals where 












neighbours and 

expectation of a state's observation is the mean of all neighbours observations [25] . The Gaussian processes are specified by their mean and covariance function [26] . Assuming that each conditional distribution is Gaussian, we will need the mean and the variance-covariance to define the CAR model. The mean and the variance- covariance are respectively defined as

Therefore, conditional probability density function of a CAR random variable 

where



where









symmetric such that

bability density function defined as

and the joint probability density function in (46) becomes

The necessary and sufficient condition for (49) to be a valid joint probability density function is that its covariance matrix should not only be symmetric, but also positive definite (that is, its eigenvalues


To show that 


where 







Suppose

then we define a matrix of interaction, 

Suppose again that the matrix 

It follows that the conditional joint probability density function can be rewritten as

where 



and the Equation (49) can be alternatively defined as

The 



The row stochasticity of 







the bounds, we replace 


If



the minimum eigenvalue of

Autoregressive model which add parametric flexibility and 



6.2. Parameter Estimation
In this study, we estimate parameters in the CAR model using Bayesian hierarchical methods. In disease mapping, we assumed that disease counts

The relative risk is defined as

Fitting the generalized linear model with a log-link function, we have


the prior distribution for 

and the prior distribution for the CAR random effect is defined by

The posterior distribution is defined as

Therefore,

The hyperperprior distribution for the precision parameters 




6.3. The Besag, York and Mollié (BYM) Model
Among the models proposed for performing risk smoothing which have appeared in literature, the [11] model has found most extensive application. The BMY model is divided into two components; the CAR model component


As noted earlier, we assume

The linear link function

Figure 12. Poisson log-normal model with CAR model: convergence diagnosis of Markov Chain Monte Carlo.
Table 6. Posterior statistics of the CAR and BYM models.
the i area is defined by

The log log-link function is defined as

where 




Parameter Estimation
We defined the likelihood function as

The prior distribution for 

prior distribution for the area-specific random effect 

and prior distribution for the CAR structure 

Therefore the posterior distribution for the parameters of interest is defined as

Therefore,

The hyperprior disribution for the precision parameters











Posterior statistics of the CAR and the BYM model are presented in Table 6. Table 6 revealed that the estimated overall relative risk effect of the CAR model is 

As noted previously, the smaller the precision variance





Although the CAR model and BYM model each provides important information about TB relative risk behaviour, we recommend the CAR model as the best fitting spatial model to Kenya TB data since it yields lower DIC (627.21) and lower pD (49.19) than the BYM model with DIC (630.76) and pD (50.97). The BYM model, though robust, its robustness as a spatial model is lost a in situation where there is over-fitting [28] . That is, adding spatially structured extra-variability to the data when such variability doe not actually exit, con- ditionally on the covariates included in the model, leads to over-fitting, and may bias the estimations of the medical association between covariates and relative risk towards the hypothesis that it has no significant effect. In other words, not accounting for an actual spatial variability may lead to major biases but if spatially, variability of health indicators is completely explained by that of the socio-economic and environmental factors taken into consideration, regression residuals could results to a biased estimate of the medical association. We therefore presents detailed results of the CAR model (43). Figure 12 shows the convergence diagnostics plots of the CAR model. The convergence diagnostics of the BYM model can be found in Figure 13 and Figure 14.
Figure 15 also shows that out of the 47 counties in Kenya, 13 exhibit TB relative risk higher than the national risk (RR = 1). Table 7 grouped counties according to their respective relative risk ranges. The pattern of risk behaviour is similar to that reported in the previous models. High TB risk occurs in the North, West, North-West and central counties of Kenya and low risk in the South-East counties except Mombasa.
Table 7 shows 4 counties (Nairobi, Mombasa, Isiolo, and Marsabit) having highest relative risk (RR > 2.0). Out of the 47 counties, 13 counties show high relative risk above 1. Counties with high TB relative risk are visually shown by the exceedence probability map Figure 16.
Figure 16 confirms with the UH model’s results that there are 13 counties elevated risk (RR > 1). These counties exhibiting high relative risk are: Nairobi, Mombasa, Kisumu, Turkan, Migori, Homa bay, Uasin Gishu, Isiolo, Marsabit, Siaya, Tharaka-Nithi, Mandera, and Embu. Again, it can be observed that North, West, North- West and central counties of Kenya exhibit high TB prevalence and low prevalence in the South-West counties except Mombasa. Figure 17 captures areas with potential clusters of disease risk. Clusters of TB risk are suspected in Marsabit, Embu, Migori and Kisumu.
6.4. Summary of the Spatial Models
The CAR and the BYM models are used to capture clustering or clusters information about disease risk. Each model identified HIV as a major cause of high TB prevalence in Kenya. Each model revealed significance of risk similarities between neighbouring counties. Local clusters of TB risk occurs in neighbouring counties with high TB relative risk. Though each of the CAR model and the BYM provides interesting information about Kenya’s TB data, CAR model appears to provide best fit since it yields lower DIC (49.19) and lower pD (627.21) than the BYM model with DIC (50.97) and pD (630.76).
7. Discussion and Conclusion
This thesis provides a framework for application of non-spatial and spatial models for modeling and mapping TB in Kenya. We discuss the non-spatial and spatial models methodology as well as illustrate application of the non-spatial and spatial methods to TB in Kenya. We have also evaluated models performance using the DIC approach proposed by [1] . Our findings reveal that the CAR and the unstructured heterogeneity models may be suitable for modeling and mapping relative risk of TB in Kenya. Table 8 presents comparison of the non-spatial models (PG, LN and UH), spatial model (CAR) and BYM model (combination of CAR and UH models) used in this study. Though the Poisson-Gamma (PG) model yields the lowest DIC, it does not allow for incorporation of spatial structure. The overall relative risk estimated by the PG is 0.94 (95% credible interval = 0.82 - 1.10). The Log-Normal (LN) provides specifications that can be extended to include spatial structures. The UH, CAR, and BYM models confirm that with all determinants of TB kept constant, overall relative risk of TB will be decreasing. Also, the UH, CAR, and BYM confirm HIV as a major TB determinant and that TB prevalence in
Figure 13. BYM model: Rubin and gelman convergence diagnostics.
Figure 14. BYM model: Rubin and gelman convergence diagnostics cont.
Figure 15. Kenya county level TB prevalence counts: The CAR model’s posterior mean of the relative risk map (a) and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
Kenya increases with increasing HIV. Generally clustering of risk and elevated risk are observed in the North, West, North-West and the central counties of Kenya and low clustering and elevated risk in the South-West counties.
The UH model captures and displays variability of relative in the study area through the area-specific random effect whiles the CAR model and the BYM model provide evidence of risk similarities between neighboring counties. Among the LN, the UH, the CAR and the BYM models, the UH model yielded the lowest DIC (622.75), hence considered as the best fitting model when fitted to Kenya TB data for 2002-2009. However, using the acceptable criteria that a DIC difference between two models greater than 10 implied significant difference while a DIC less than 5 implied a negligible difference [29] , one could use any of the non-spatial and spatial models for fitting Kenya TB data for 2002-2009 depending on the issue at hand. Although these approaches are less than ideal, we hope that our results provide a useful starting point into the development of
Table 7. Poisson log-normal model with CAR model results indicating counties with high and low TB risk.
Figure 16. Kenya county level TB prevalence counts: The CAR model posterior mean of the relative risk exceedence probability map (a) and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
Figure 17. The correlated heterogeneity effect’s posterior map (a) and its 2.5% quantile (b), median (c) and 97.5% quantile (d).
spatial methodology for modeling and mapping RR of TB in Kenya.
Modeling of risk in space and time is important but is quite a challenging task. Further research is required determined suitable spatio-temporal models for modeling and mapping relative risk of TB in Kenya. This will allow to explain evolution of the relative risk of TB in space and time.
Limitation of the study is that the specification of the adjacency matrix 



Table 8. Posterior statistics of non-spatial and spatial models.
convergence of the parameters draw, due to potentially improper distributional assumptions. Conceptually, not including 
Cite this paper
Abdul-Karim Iddrisu,Yaw Ampem Amoako, (2016) Spatial Modeling and Mapping of Tuberculosis Using Bayesian Hierarchical Approaches. Open Journal of Statistics,06,482-513. doi: 10.4236/ojs.2016.63043
References
- 1. Spiegelhalter, D.J., Best, N.G., Carlin, B.P. and Van Der Linde, A. (2002) Bayesian Measures of Model Complexity and Fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64, 583-639.
- 2. López-Quilez, A. and Munoz, F. (2009) Review of Spatio-Temporal Models for Disease Mapping.
- 3. Currie, C.S.M., Williams, B.G., Cheng, R.C.H. and Dye, C. (2003) Tuberculosis Epidemics Driven by Hiv: Is Prevention Better than Cure? Aids, 17, 2501-2508.
http://dx.doi.org/10.1097/00002030-200311210-00013 - 4. Bernardinelli, L., Clayton, D., Pascutto, C., Montomoli, C., Ghislandi, M. and Songini, M. (1995) Bayesian Analysis of Space-Time Variation in Disease Risk. Statistics in Medicine, 14, 2433-2443.
- 5. Waller, L.A., Carlin, B.P., Xia, H. and Gelfand, A.E. (1997) Hierarchical Spatio-Temporal Mapping of Disease Rates. Journal of the American Statistical Association, 92, 607-617.
http://dx.doi.org/10.1080/01621459.1997.10474012 - 6. Elliott, P., Wakefield, J., Best, N., Briggs, D., et al. (2000) Spatial Epidemiology: Methods and Applications. Oxford University Press.
- 7. Lawson, A.B. and Lawson, A.B. (2001) Statistical Methods in Spatial Epidemiology. John Wiley, Hoboken.
- 8. Knorr-Held, L. (1999) Bayesian Modelling of Inseparable Space-Time Variation in Disease Risk. Statistics in Medicine, 19, 2555-2567.
- 9. Lawson, A.B. (2008) Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology. CRC Press..
- 10. Clayton, D. and Kaldor, J. (1987) Empirical Bayes Estimates of Age-Standardized Relative Risks for Use in Disease Mapping. Biometrics, 671-681.
- 11. Besag, J., York, J. and Mollié, A. (1991) Bayesian Image Restoration, with Two Applications in Spatial Statistics. Journal of Applied Statistics, 5-6, 21-59.
- 12. da Roza, D.L., do Carmo Gullaci Caccia-Bava, M., Martinez, E.Z., et al. (2012) Spatiotemporal Patterns of Tuberculosis Incidence in Ribeirao Preto, State of Sao Paulo, Southeast Brazil, and Their Relationship with Social Vulnerability: A Bayesian Analysis. Revista da Sociedade Brasileira de Medicina Tropical, 45, 607-615.
http://dx.doi.org/10.1590/S0037-86822012000500013 - 13. Randremanana, R., Richard, V., Rakotomanana, F., Sabatier, P. and Bicout, D. (2010) Bayesian Mapping of Pulmonary Tuberculosis in Antananarivo, Madagascar. BMC Infectious Diseases, 10, 21.
http://dx.doi.org/10.1186/1471-2334-10-21 - 14. Achcar, E.Z., Martinez, A., Ruffino-Netto, J.A., Paulino, C.D. and Soares, P. (2008) A Statistical Model Investigating the Prevalence of Tuberculosis in New York City Using Counting Processes with Two Change-Points. Epidemiology and Infection, 136, 1599.
http://dx.doi.org/10.1017/S0950268808000526 - 15. Srinivasan, R., Venkatesan, P. and Dharuman, C. (2012) Bayesian Conditional Auto Regressive Model for Mapping Tuberculosis Prevalence in India. International Journal of Pharmaceutical Studies and Research.
- 16. Ntzoufras, I. (2011) Bayesian Modeling Using WinBUGS. Vol. 698, Wiley, Hoboken.
- 17. Wakefield, N.G., Best, J.C. and Waller, L. (2000) Bayesian Approaches to Disease Mapping. Spatial Epidemiology: Methods and Applications, 104-107.
- 18. Lawson, A.B., Browne, W.J. and Vidal Rodeiro, C.L. (2003) Disease Mapping with WinBUGS and MLwiN. Vol. 11. Wiley, Hoboken.
- 19. Gill, J. (2002) Bayesian Methods: A Social and Behavioral Sciences Approach. Vol. 20, CRC Press.
- 20. Miller, H.J. (2004) Tobler’s First Law and Spatial Analysis. Annals of the Association of American Geographers, 94, 284-289.
http://dx.doi.org/10.1111/j.1467-8306.2004.09402005.x - 21. Geman, S. and Geman, D. (1984) Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 6, 721-741.
- 22. Kyung, M. and Ghosh, S.K. (2009) Bayesian Inference for Directional Conditionally Autoregressive Models. Bayesian Analysis, 4, 675-706.
- 23. Besag, J. (1974) Spatial Interaction and the Statistical Analysis of Lattice Systems (with Discussion). Journal of the Royal Statistical Society: Series B, 36, 192-236.
- 24. Cressie, N.A.C. (1993) Statistics for Spatial Data. Revised Edition, Vol. 928, Wiley, New York.
- 25. Mariella, L. and Tarantino, M. (2010) Spatial Temporal Conditional Auto-Regressive Model: A New Autoregressive Matrix. Australian Journal of Statistics, 39, 223.
- 26. Waller, L.A. and Gotway, C.A. (2004) Applied Spatial Statistics for Public Health Data. Vol. 368, Wiley-Interscience.
- 27. Banerjee, S. (2009) Spatial Autoregressive Models.
- 28. Latouche, A., Guihenneuc-Jouyaux, C., Girard, C. and Hemon, D. (2007) Robustness of the Bym Model in Absence of Spatial Variation in the Residuals. International Journal of Health Geographics, 6, 1.
- 29. Best, N. (2011) Bayesian Hierarchical Modelling Using Winbugs.
- 30. Wang, Y.Y. and Kockelman, K.M. (2013) A Poisson-Lognormal Conditional-Autoregressive Model for Multivariate Spatial Analysis of Pedestrian Crash Counts across Neighborhoods. Accident Analysis & Prevention, 60, 71-84.
http://dx.doi.org/10.1016/j.aap.2013.07.030





















