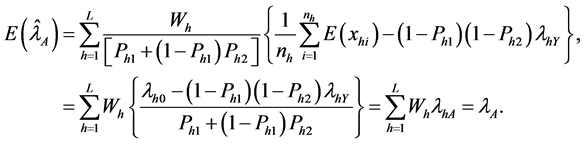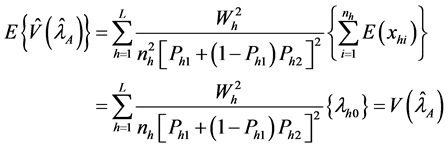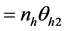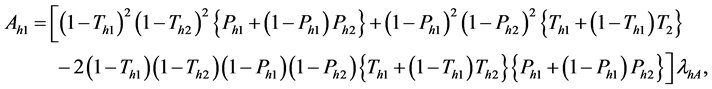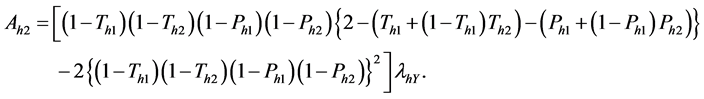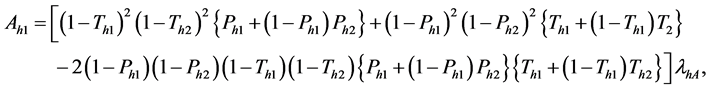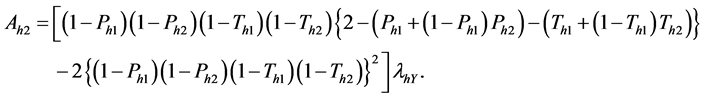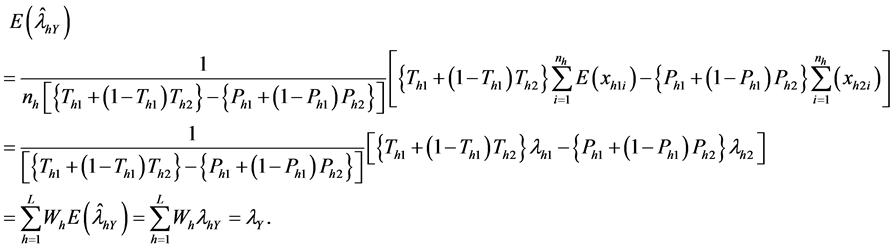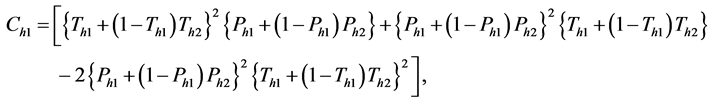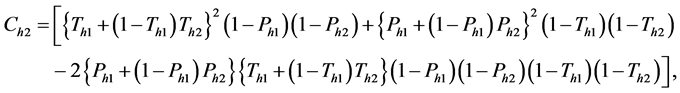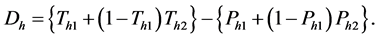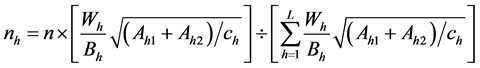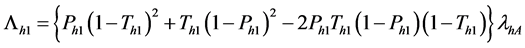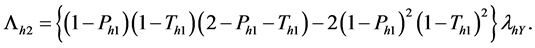Open Journal of Statistics
Vol.06 No.01(2016), Article ID:63653,11 pages
10.4236/ojs.2016.61011
Improved Estimation of Rare Sensitive Attribute in a Stratified Sampling Using Poisson Distribution
Abdul Wakeel, Masood Anwar
Department of Mathematics, COMSATS Institute of Information Technology, Islamabad, Pakistan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 December 2015; accepted 20 February 2016; published 23 February 2016
ABSTRACT
In this study, we propose a two stage randomized response model. Improved unbiased estimators of the mean number of persons possessing a rare sensitive attribute under two different situations are proposed. The proposed estimators are evaluated using a relative efficiency comparison. It is shown that our estimators are efficient as compared to existing estimators when the parameter of rare unrelated attribute is known and in unknown case, depending on the probability of selecting a question.
Keywords:
Poisson Distribution, Rare Sensitive Attribute, Rare Unrelated Attribute, Stratified Sampling

1. Introduction
The collection of data through direct questioning on rare sensitive issues such as extramarital affairs, family disturbances and declaring religious affiliation in extremism condition is far-reaching issue. Warner [1] introduced the randomized response procedure to procure trustworthy data for estimating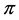 , the proportion of respondents in the population belonging to the sensitive group. Greenberg et al. [2] suggested an unrelated question randomized response model in which each individual selected in the samples was asked to reply “yes” or “no” to one of two statements: (a) Do you belong to Group A? (b) Do you belong to Group Y? with respective probabilities P and
, the proportion of respondents in the population belonging to the sensitive group. Greenberg et al. [2] suggested an unrelated question randomized response model in which each individual selected in the samples was asked to reply “yes” or “no” to one of two statements: (a) Do you belong to Group A? (b) Do you belong to Group Y? with respective probabilities P and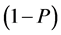 . Second question asked in the sampling does not have any effect on the first question. Greenberg et al. [2] considered
. Second question asked in the sampling does not have any effect on the first question. Greenberg et al. [2] considered 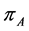 and
and 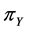 the proportion of persons possessing sensitive and unrelated characteristic respectively and discussed both the cases when
the proportion of persons possessing sensitive and unrelated characteristic respectively and discussed both the cases when 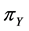 was known and unknown. The probability of yes responses
was known and unknown. The probability of yes responses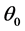 , defined by them is
, defined by them is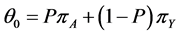 . Mangat and Singh [3] proposed a two stage randomized response procedure which required the use of two randomization devices. The random device
. Mangat and Singh [3] proposed a two stage randomized response procedure which required the use of two randomization devices. The random device 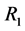 consists of two statements namely (a) I belong to the sensitive group, and (b) Go to random device
consists of two statements namely (a) I belong to the sensitive group, and (b) Go to random device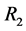 , with probabilities T and
, with probabilities T and 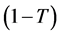 respectively. The random device
respectively. The random device 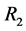 which uses two statements (a) I belong to the sensitive group, and (b) I do not belong to the sensitive group with known probabilities P and
which uses two statements (a) I belong to the sensitive group, and (b) I do not belong to the sensitive group with known probabilities P and 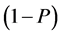 respectively. Then
respectively. Then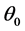 , the probability of yes responses is
, the probability of yes responses is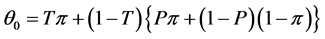 .
.
Later on, different modifications have been made to improve the methodology for collection of information. Some of them are Lee et al. [4] , Chaudhuri and Mukerjee [5] , Mahmood et al. [6] , Land et al. [7] , Bhargava and Singh [8] .
Land et al. [7] proposed the estimators for the mean number of persons possessing the rare sensitive attribute using the unrelated question randomized response model by utilizing a Poisson distribution. Recently, Lee et al. [4] extended the Land et al.’s [7] study to stratify sampling and propose the estimators when the parameter of rare unrelated attribute is known and unknown.
In this study, we propose improved estimators for the mean and its variance of the number of persons possessing a rare sensitive attribute based on stratified sampling by using Poisson distribution. The estimators are proposed when the parameter of the rare unrelated attribute is known and unknown. The proposed estimators are evaluated using a relative efficiency comparing the variances of the estimators reported in Lee et al. [4] .
2. Improved Estimation of a Rare Sensitive Attribute in Stratified Sampling-Known Rare Unrelated Attributes
Consider the population of size N individuals which is divided into L subpopulations (strata) of sizes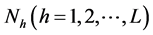 . All the subpopulations are disjoint and together comprise the whole population. In stratum h,
. All the subpopulations are disjoint and together comprise the whole population. In stratum h, 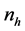
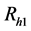
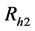
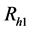
(i) “I possessrare sensitive attribute A”
(ii) “Go to randomization device Rh2”
with respective probabilities 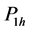
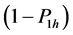
The randomization device 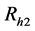
(i) “I possess rare sensitive attribute A”
(ii) “I possess rare unrelated attribute Y”
with probabilities 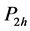
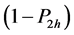
By this randomized device, the probability of a yes response in stratum h is given by
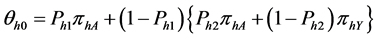
where 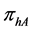
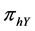
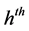
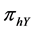
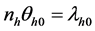
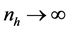
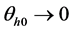
Let 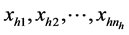
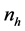
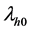
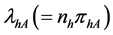
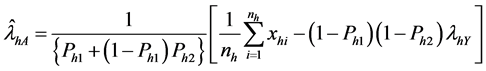
where 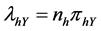
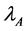
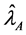
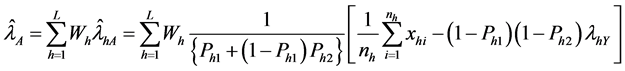
where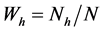
The variance of the estimator 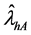
where
Thus, the variance expression of the estimator 
THEOREM 1. 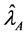
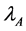
Proof. From (3), we have
THEOREM 2. The unbiased estimator for 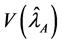
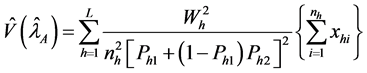
Proof.
Now, we consider the proportional and optimal allocations of the total sample size n into different strata. The method of proportional allocation is used to define sample sizes in each stratum depending on each stratum size. Since the sample size in each stratum is defined as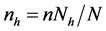
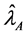
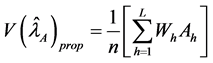
However, the optimal allocation is a technique to define sample size to minimize variance for a given cost or to minimize the cost for a specified variance. The 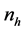
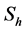
riable. In stratified sampling, let cost function is defined as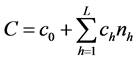
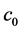
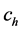
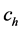
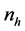
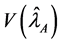
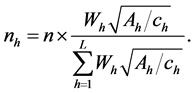
So the minimum variance of the estimator for the specified cost C under the optimum allocation of sample size is given by
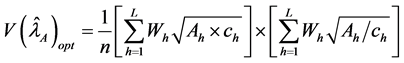
3. Improved Estimation of a Rare Sensitive Attribute in Stratified Sampling-Unknown Rare Unrelated Attributes
In this section, the estimators for the mean number of rare sensitive attribute are proposed under the assumptions that the sizes of stratum are known; however, 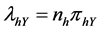
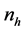
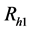
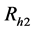
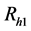
(i) “I possess a sensitive group A”
(ii) “Go to randomization device Rh2”
The statements occur with respective probabilities 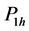
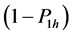
The two statements of the randomization device 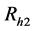
(i) “I possess a sensitive attribute A”
(ii) “I possess unrelated attribute Y”
represented with respective probabilities 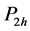
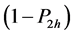
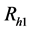
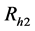
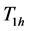
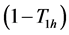
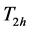
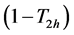
The probabilities of the yes responses for the first and second use of pair of randomization devices are respectively given by
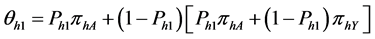
and
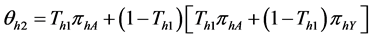
where 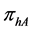
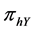
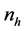
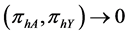
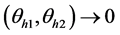
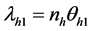
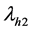
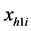
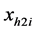
Following the expression given in Equations (12) and (13), we have the sample means for both set of responses as
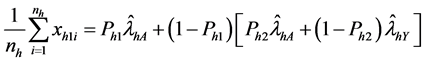
and
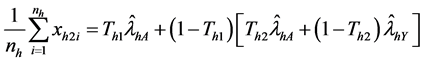
By solving (15) and (16), we get estimators of 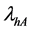
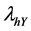
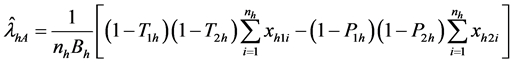
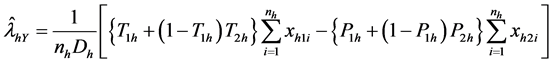
where
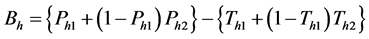
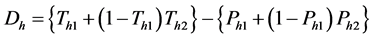
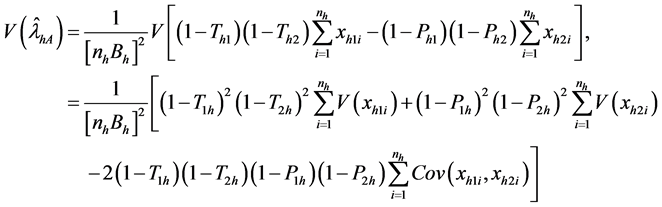
Puttinng (12), (13) and (14) in (19) we get
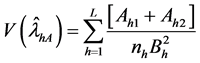
where
The stratified estimators of 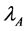
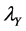
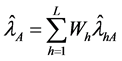
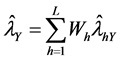
THEOREM 3. 
Proof.
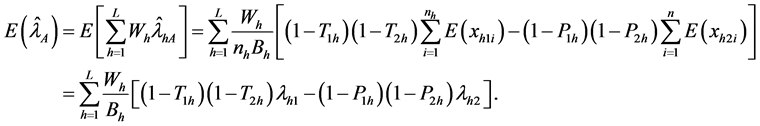
Putting the values of 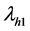
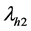
THEOREM 4. The variance of 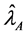
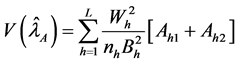
where
Proof. Since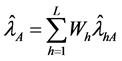
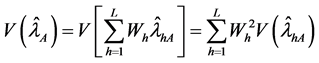
On putting (20) in (24) we have the theorem.
Corollary 1: An unbiased estimator for the variance of rare sensitive attribute is given by
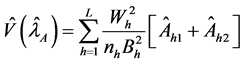
It can be proved easily.
THEOREM 5. 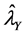
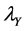
Proof. From (18), we have
Corollary 2: An unbiased estimator for 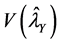
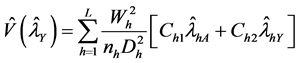
where
Now under proportional allocation of sample size, the variance of 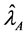
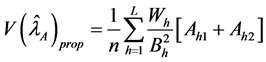
However, in optimum allocation, the sample size in stratum h is
and the variance of 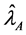
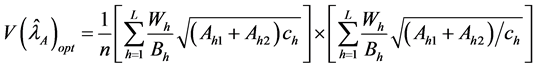
4. Relative Efficiency
Lee et al. [4] proposed variance of 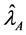
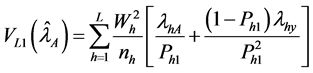
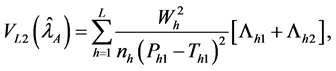
where
For comparison of the proposed estimator with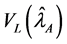
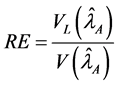
Large samples are required to estimate the means of rare sensitive attribute. So we consider a large hypothetical population, in order to study the relative efficiency, setting 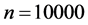
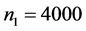
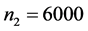
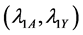
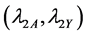
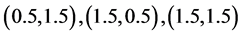
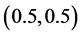
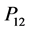
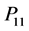
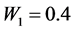
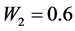
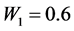
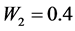
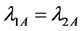
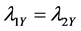
4.1. Relative Efficiency When Rare Unrelated Attribute Is Known
Let 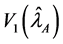
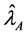
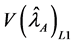
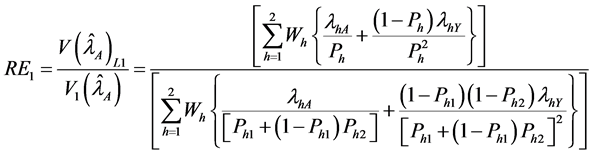
From Equation (29) it evident that the relative efficiency of proposed estimator is free from the sample size n. We set the design probabilities as 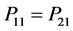
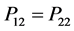
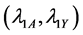
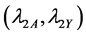
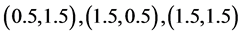
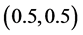
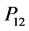
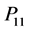
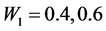
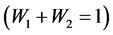
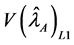
4.2. Relative Efficiency When Rare Unrelated Attribute Is Unknown
Let 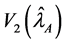
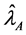
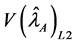
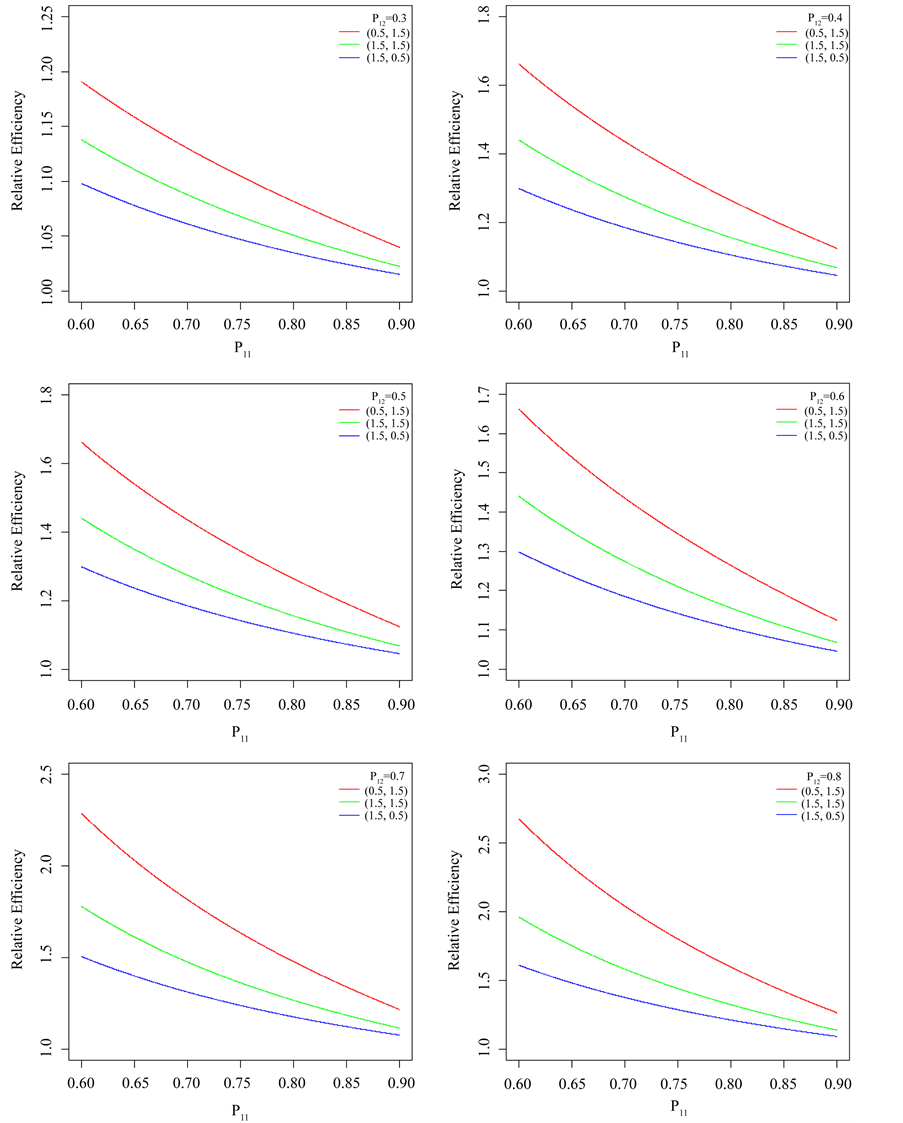
Figure 1. Relative Efficiency (RE) of the proposed model with respect to Lee et al. [4] for W1 = 0.4 and P12 = 0.3 to 0.8.
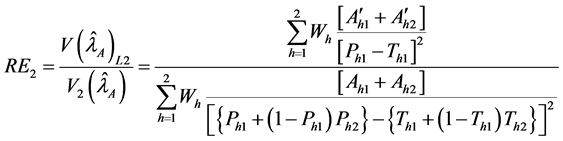
The relative efficiency of proposed estimator is free from the sample size n. For the analysis, the design probabilities are fixed as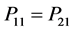
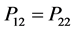
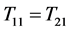
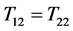
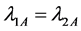
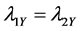
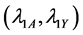
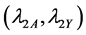
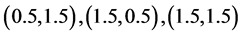
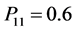
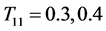
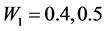
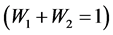
estimator outer perform than 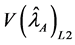
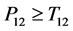
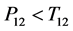
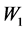
Table 1. Relative efficiency of the proposed estimator with Lee et al. (2013).
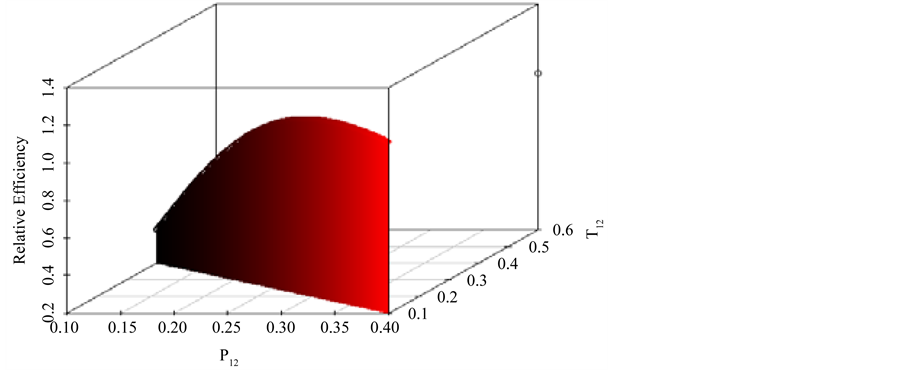
Figure 2. Relative Efficiency (RE) of the proposed model with respect to Lee et al. [4] for indicated values.
Table 2. Relative efficiency of the proposed estimator with Lee et al. (2013), W1 = 0.4, and W1 = 0.5.
5. Conclusion
In this study, a two stage randomized response model is proposed with improved estimators for the mean and its variance of the number of persons possessing a rare sensitive attribute based on stratified sampling by using Poisson distribution. It is shown that our proposed method have better efficiencies than the existing randomized response model, when the parameter of rare unrelated attribute is known and in unknown case, depending on the probability of selecting a question. For future work, we can obtain more sensitive information from respondents by using stratified double sampling with the proposed model.
Cite this paper
AbdulWakeel,MasoodAnwar, (2016) Improved Estimation of Rare Sensitive Attribute in a Stratified Sampling Using Poisson Distribution. Open Journal of Statistics,06,85-95. doi: 10.4236/ojs.2016.61011
References
- 1. Bhargava, M. and Singh, R. (2000) A Modified Randomization Device for Warner’s Model. Statistica, 60, 315-321.
- 2. Land, M., Singh, S. and Sedory, S.A. (2012) Estimation of a Rare Sensitive Attribute Using Poisson Distribution. Statistics, 46, 351-360.
http://dx.doi.org/10.1080/02331888.2010.524300 - 3. Mahmood, M., Singh, S. and Horn, S. (1998) On the Confidentiality Guaranteed under Randomized Response Sampling: A Comparison with Several New Techniques. Biometrical Journal, 40, 237-242.
http://dx.doi.org/10.1002/(SICI)1521-4036(199806)40:2<237::AID-BIMJ237>3.0.CO;2-N - 4. Chaudhuri, A. and Mukerjee, R. (1988) Randomized Response: Theory and Techniques. Marcel Dekker, New York.
- 5. Lee, G.S., Uhm, D. and Kim, J.M. (2013) Estimation of a Rare Sensitive Attribute in a Stratified Sample Using Poisson Distribution. Statistics, 47, 685-709.
http://dx.doi.org/10.1080/02331888.2011.625503 - 6. Mangat, N.S. and Singh, R. (1990) On the Confidentiality Guaranteed under Randomized Response Sampling: A Comparison with Several New Techniques. Biometrical Journal, 40, 237-242.
- 7. Greenberg, B.G., Abul-Ela, A.L.A., Simmons, W.R. and Horvitz, D.G. (1969) The Unrelated Question Randomized Response Model: Theoretical Framework. Journal of the American Statistical Association, 64, 520-539.
http://dx.doi.org/10.1080/01621459.1969.10500991 - 8. Warner, S.L. (1965) Randomized Response: A Survey Technique for Eliminating Evasive Answer Bias. Journal of Computational and Graphical Statistics, 60, 63-66.
http://dx.doi.org/10.1080/01621459.1965.10480775