Open Journal of Statistics
Vol.05 No.06(2015), Article ID:60682,14 pages
10.4236/ojs.2015.56060
Bayesian Prediction of Future Generalized Order Statistics from a Class of Finite Mixture Distributions
Abd EL-Baset A. Ahmad1, Areej M. Al-Zaydi2
1Department of Mathematics, Assiut University, Assiut, Egypt
2Department of Mathematics, Taif University, Taif, Saudi Arabia
Email: abahmad2002@yahoo.com, aree.m.z@hotmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 August 2015; accepted 25 October 2015; published 28 October 2015
ABSTRACT
This article is concerned with the problem of prediction for the future generalized order statistics from a mixture of two general components based on doubly type II censored sample. We consider the one sample prediction and two sample prediction techniques. Bayesian prediction intervals for the median of future sample of generalized order statistics having odd and even sizes are obtained. Our results are specialized to ordinary order statistics and ordinary upper record values. A mixture of two Gompertz components model is given as an application. Numerical computations are given to illustrate the procedures.
Keywords:
Generalized Order Statistics, Bayesian Prediction, Heterogeneous Population, Doubly Type II Censored Samples, One- and Two-Sample Schemes

1. Introduction
Let the random variable (rv) T follows a class including some known lifetime models; its cumulative distribution function (CDF) is given by
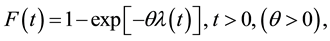 (1)
(1)
and its probability density function (PDF) is given by
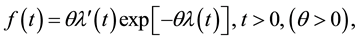 (2)
(2)
where  is the derivative of
is the derivative of 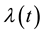 with respect to t and
with respect to t and 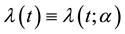 is a nonnegative continuous function of t and α may be a vector of parameters, such that
is a nonnegative continuous function of t and α may be a vector of parameters, such that
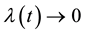 as
as  and
and 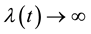 as
as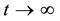 .
.
The reliability function (RF) and hazard rate function (HRF) are given, respectively, by
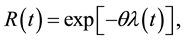 (3)
(3)
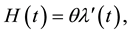 (4)
(4)
where 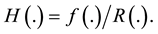
The general problem of statistical prediction may be described as that of inferring the value of unknown observable that belongs to a future sample from current available information, known as the informative sample. As in estimation, a predictor can be either a point or an interval predictor. The problem of prediction can be solved fully within Bayesian framework [1] .
Prediction has been applied in medicine, engineering, business and other areas as well. For details on the history of statistical prediction, analysis, application and examples see for example [1] [2] .
Bayesian prediction of future order statistics and records from different populations has been dealt with by many authors. Among others, [3] predicted observables from a general class of distributions. [4] obtained Bayesian prediction bounds under a mixture of two exponential components model based on type I censoring. [5] obtained Bayesian predictive survival function of the median of a set of future observations. Bayesian prediction bounds based on type I censoring from a finite mixture of Lomax components were obtained by [6] . [7] obtained Bayesian predictive density of order statistics based on finite mixture models. [8] obtained Bayesian interval prediction of future records. Based on type I censored samples, Bayesian prediction bounds for the sth future observable from a finite mixture of two component Gompertz life time model were obtained by [9] . [10] considered Bayes inference under a finite mixture of two compound Gompertz components model. Bayesian prediction of future median has been studied by, among others, they were [5] [11] [12] .
Recently, [13] introduced the generalized order statistics (GOS’S). Ordinary order statistics, ordinary record values and sequential order statistics were, among others, special cases of GOS’S. For various distributional properties of GOS’S, see [13] . The GOS’S have been considered extensively by many authors, among others, they were [14] -[33] .
Mixtures of distributions arise frequently in life testing, reliability, biological and physical sciences. Some of the most important references that discuss different types of mixtures of distributions are a monograph by [34] -[36] .
The PDF, CDF, RF and HRF of a finite mixture of two components of the class under study are given, respectively, by
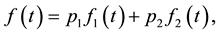 (5)
(5)
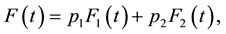 (6)
(6)
 (7)
(7)
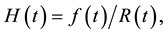 (8)
(8)
where, for







The property of identifiability is an important consideration on estimating the parameters in a mixture of distributions. Also, testing hypothesis, classification of random variables, can be meaning fully discussed only if the class of all finite mixtures is identifiable. Idenifiability of mixtures has been discussed by several authors, including [37] -[39] .
This article is concerned with the problem of obtaining Bayesian prediction intervals (BPI) for the future GOS’S from a mixture of two general components based on doubly type II censored sample. One- and two-sam- ple prediction cases are treated in Sections 2 and 3, respectively. Bayesian prediction intervals for the median of future sample of GOS’S having odd and even sizes are obtained in Sections 4. A mixture of two Gompertz components is given as an application in Section 5. Finally, numerical computations are given in Section 6.
2. One Sample Prediction
Let 

ponents of the class (2). Based on this doubly censored sample, the likelihood function can be written (see [27] ) as

where


For definition and various distributional properties of GOS’S, see [13] .
By substituting Equations (1) and (5) in Equation (9), we get
for

And for

We shall use the conjugate prior density, that was suggested by [3] , in the following form

where 
Then the posterior PDF of


Substituting from Equations (10) and (12) in Equation (13), for


where
For

Now, suppose that the first 

we wish to predict the future GOS’S 


conditional PDF of the 


where
When

In the case when

The predictive PDF of 


where for

where
Also, for

It then follows that the predictive survival function is given, for the 

A 

where 



3. Two Sample Prediction
Suppose that
Be a doubly type II censored random sample drawn from a population whose CDF, 


Be a second independent generalized ordered random sample (of size N) of future observations from the same distribution. Based on such a doubly type II censored sample, we wish to predict the future GOS 
It was shown by [32] that the PDF of GOS 

where 
Substituting from Equations (1) and (5) in (25), we have

The predictive PDF of 

where for

where
Also for

Bayesian prediction bounds for


A 

where 



4. Bayesian Prediction for the Future Median
The median of N observations, denoted by

where 

4.1. The Case of Odd Future Sample Size
The PDF of future median 


Substituting 

observations.
A 

where 



where, for 


4.2. The Case of Even Future Sample Size
The joint density function of two consecutive GOS 


where
And

Expanding 



By substituting Equations (2), (4) and (5) in Equation (36) and integrating out z, yields the density function of


In the case

The predictive density function of the future median of 

where 

that the predictive survival function is given, for

The lower and upper bound of 

5. Example
Gompertz Components
Suppose that, for 


In this case, the 








where 

5.1.1. One Sample Prediction
For 


And Equation (41) in Equation (22) and solving, numerically, Equations (23) and (24) we can obtain the lower and upper bounds of BPI.
Special Cases
1) Upper order statistics
The predictive PDF (19), when 


where
Substituting from Equation (42) in Equation (22) and solving Equations (23) and (24), numerically, we can obtain the bounds of BPI.
2) Upper record values
When

where
Substituting from Equation (43) in Equation (22) and solving Equations (23) and (24), numerically, we can obtain the bounds of BPI.
5.1.2. Two Sample Prediction
For 




Special Cases
1) Upper order statistics
Substituting 


where
To obtain 

2) Upper record values
In Equation (27), by putting


where
Substituting from Equation (45) in Equation (30) and solving Equations (31) and (32), numerically, we can obtain the bounds of BPI.
5.1.3. Prediction for the Future Median (the Case of Odd N)
Special Cases
1) Upper order statistics
Substituting








where
To obtain 

2) Upper record values
The predictive PDF (27), when

where
To obtain 

5.1.4. Prediction for the Future Median (the Case of Even N)
Special Cases
1) Upper order statistics
The predictive PDF and survival function of 


2) Upper record values
The predictive PDF and survival function of 

To obtain 
We solve Equations (33) and (34), numerically.
6. Numerical Computations
In this section, 95% BPI for future observations from a mixture of two
6.1. One Sample Prediction
In this subsection, we compute 95% BPI for
1) For a given values of the prior parameters 

2) For a given values of the prior parameters



3) Using the generated values of 



・ generate two observations 

・ if


・ repeat above steps n times to get a sample of size n;
・ the sample obtained in above steps is ordered.
4) Using the generated values of 



5) The 95% BPI for the future observations are obtained by solving numerically, Equations (23) and (24) with
6.2. Two Sample Prediction
In this subsection, we compute 95% BPI for two sample prediction in the two cases ordinary order statistics and ordinary upper record values according to the following steps:
1) For a given values of the prior parameters 

2) For a given values of the prior parameters for 


3) Using the generated values of 


4) The 95% BPI for the observations from a future independent sample of size N are obtained by solving numerically, Equations (31) and (32) with
5) Generate 10,000 samples each of size N from a mixture of two 

6) Different sample sizes n and N are considered.
6.3. Prediction for the Future Median
In this subsection, 95% BPI for the median of N future observations are obtained when the underlying population distribution is a mixture of two Gompertz components in the two cases ordinary order statistics and ordinary upper record values according to the following steps:
1) For a given values of the prior parameters 

2) For a given values of the prior parameters



3) Using the generated values of 


4) The 95% BPI for the median of N of future observations are obtained by solving numerically, Equations (33) and (34) with 


5) Generate 10,000 samples each of size N from a mixture of two 

6) The prediction are conducted on the basis of a doubly type II censored samples and type II censored samples.
The computational (our) results were computed by using Mathematica 6.0. When the prior parameters chosen as b1 = 1.5, b2 = 2, d1 = 1, d2 = 2 which yield the generated values of 
Table 1. 95% BPI for future order statistics


Table 2. 95% BPI for the future upper record values

Table 3. 95% BPI and PC for the future order statistics

sample predictions, respectively. In Table 5 and Table 6, 95% BPI for the medians of future samples with odd or even sizes are computed. Our results are specialized to ordinary order statistics and ordinary upper record values.
Table 4. 95% BPI and PC for future ordinary upper record values

Table 5. (Ordinary order statistics) 95% BPI and PC for future median 



Table 6. (Ordinary upper record values) 95% BPI and PC for future median 



6.4. Conclusions
1) Bayes prediction intervals for future observations are obtained using a one-sample and two-sample schemes based on a finite mixture of two Gompertz components model. Our results are specialized to ordinary order statistics and ordinary upper record values.
2) Bayesian prediction intervals for the medians of future samples with odd or even sizes are obtained based on a finite mixture of two Gompertz components model. Our results are specialized to ordinary order statistics and ordinary upper record values.
3) It is evident from all tables that the lengths of the BPI decrease as the sample size increase.
4) In general, if the sample size n and censored size r are fixed the lengths of the BPI increase by increasing s.
5) For fixed sample size n, censored size r and s, the lengths of the BPI increase by increasing a or b.
6) The percentage coverage improves by the use of a large number of observed values.
Cite this paper
Abd EL-BasetA. Ahmad,Areej M.Al-Zaydi, (2015) Bayesian Prediction of Future Generalized Order Statistics from a Class of Finite Mixture Distributions. Open Journal of Statistics,05,585-599. doi: 10.4236/ojs.2015.56060
References
- 1. Geisser, S. (1993) Predictive Inference: An Introduction. Chapman and Hall, London.
http://dx.doi.org/10.1007/978-1-4899-4467-2 - 2. Aitchison, J. and Dunsmore, I.R. (1975) Statistical Prediction Analysis. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511569647 - 3. AL-Hussaini, E.K. (1999) Prediction, Observables from a General Class of Distributions. Journal of Statistical Planning and Inference, 79, 79-91.
http://dx.doi.org/10.1016/S0378-3758(98)00228-6 - 4. AL-Hussaini, E.K. (1999) Bayesian Prediction under a Mixture of Two Exponential Components Model Based on Type I Censoring. Journal of Applied Statistical Science, 8, 173-185.
- 5. AL-Hussaini, E.K. (2001) On Bayesian Prediction of Future Median. Communications in Statistics—Theory and Methods, 30, 1395-1410.
http://dx.doi.org/10.1081/STA-100104752 - 6. AL-Hussaini, E.K., Nigm, A.M. and Jaheen, Z.F. (2001) Bayesian Prediction Based on Finite Mixtures of Lomax Components Model and Type I Censoring. Statistics, 35, 259-268.
http://dx.doi.org/10.1080/02331880108802735 - 7. AL-Hussaini, E.K. (2003) Bayesian Predictive Density of Order Statistics Based on Finite Mixture Models. Journal of Statistical Planning and Inference, 113, 15-24.
http://dx.doi.org/10.1016/S0378-3758(01)00297-X - 8. AL-Hussaini, E.K. and Ahmad, A.A. (2003) On Bayesian Interval Prediction of Future Records. Test, 12, 79-99.
http://dx.doi.org/10.1007/BF02595812 - 9. Jaheen, Z.F. (2003) Bayesian Prediction under a Mixture of Two-Component Gompertz Lifetime Model. Test, 12, 413-426. http://dx.doi.org/10.1007/BF02595722
- 10. AL-Hussaini, E.K. and AL-Jarallah, R.A. (2006) Bayes Inference under a Finite Mixture of Two Compound Gompertz Components Model. Cairo University, Giza.
- 11. AL-Hussaini, E.K. and Osman, M.I. (1997) On the Median of a Finite Mixture. Journal of Statistical Computation and Simulation, 58, 121-144.
http://dx.doi.org/10.1080/00949659708811826 - 12. AL-Hussaini, E.K. and Jaheen, Z.F. (1999) Parametric Prediction Bounds for the Future Median of the Exponential Distribution. Statistics: A Journal of Theoretical and Applied Statistics, 32, 267-275.
http://dx.doi.org/10.1080/02331889908802667 - 13. Kamps, U. (1995) A Concept of Generalized Order Statistics. Journal of Statistical Planning and Inference, 48, 1-23.
http://dx.doi.org/10.1016/0378-3758(94)00147-N - 14. Ahsanullah, M. (1996) Generalized Order Statistics from Two Parameter Uniform Distribution. Communications in Statistics: Theory and Methods, 25, 2311-2318.
http://dx.doi.org/10.1080/03610929608831840 - 15. Ahsanullah, M. (2000) Generalized Order Statistics from Exponential Distribution. Journal of Statistical Planning and Inference, 85, 85-91.
http://dx.doi.org/10.1016/S0378-3758(99)00068-3 - 16. Kamps, U. and Gather, U. (1997) Characteristic Property of Generalized Order Statistics for Exponential Distributions. Applicationes Mathematicae, 24, 383-391.
- 17. Cramer, E. and Kamps, U. (2000) Relations for Expectations of Functions of Generalized Order Statistics. Journal of Statistical Planning and Inference, 89, 79-89.
http://dx.doi.org/10.1016/S0378-3758(00)00074-4 - 18. Cramer, E. and Kamps, U. (2001) On Distributions of Generalized Order Statistics. Statistics: A Journal of Theoretical and Applied Statistics, 35, 269-280.
http://dx.doi.org/10.1080/02331880108802736 - 19. Habibullah, M. and Ahsanullah, M. (2000) Estimation of Parameters of a Pareto Distribution by Generalized Order Statistics. Communications in Statistics: Theory and Methods, 29, 1597-1609.
http://dx.doi.org/10.1080/03610920008832567 - 20. AL-Hussaini, E.K. and Ahmad, A.A. (2003) On Bayesian Interval Prediction of Future Records. Test, 12, 79-99.
http://dx.doi.org/10.1007/BF02595812 - 21. AL-Hussaini, E.K. and Ahmad, A.A. (2003) On Bayesian Predictive Distributions of Generalized Order Statistics. Metrika, 57, 165-176.
http://dx.doi.org/10.1007/s001840200207 - 22. AL-Hussaini, E.K. (2004) Generalized Order Statistics: Prospective and Applications. Journal of Applied Statistical Science, 13, 59-85.
- 23. Jaheen, Z.F. (2002) On Bayesian Prediction of Generalized Order Statistics. Journal of Statistical Theory and Applications, 1, 191-204.
- 24. Jaheen, Z.F. (2005) Estimation Based on Generalized Order Statistics from the Burr Model. Communications in Statistics: Theory and Methods, 34, 785-794.
http://dx.doi.org/10.1081/STA-200054408 - 25. Ahmad, A.A. (2007) Relations for Single and Product Moments of Generalized Order Statistics from Doubly Truncated Burr Type XII Distribution. Journal of the Egyptian Mathematical Society, 15, 117-128.
- 26. Ahmad, A.A. (2008) Single and Product Moments of Generalized Order Statistics from Linear Exponential Distribution. Communications in Statistics: Theory and Methods, 37, 1162-1172.
http://dx.doi.org/10.1080/03610920701713344 - 27. Ahmad, A.A. (2011) On Bayesian Interval Prediction of Future Generalized Order Statistics Using Doubly Censoring. Statistics: A Journal of Theoretical and Applied Statistics, 45, 413-425.
http://dx.doi.org/10.1080/02331881003650123 - 28. Ateya, S.F. and Ahmad, A.A. (2011) Inferences Based on Generalized Order Statistics under Truncated Type I Generalized Logistic Distribution. Statistics: A Journal of Theoretical and Applied Statistics, 45, 389-402.
http://dx.doi.org/10.1080/02331881003650149 - 29. Abu-Shal, T.A. and AL-Zaydi, A.M. (2012) Estimation Based on Generalized Order Statistics from a Mixture of Two Rayleigh Distributions. International Journal of Statistics and Probability, 1, 79-90.
- 30. Abu-Shal, T.A. and AL-Zaydi, A.M. (2012) Bayesian Prediction Based on Generalized Order Statistics from a Mixture of Two Exponentiated Weibull Distribution via MCMC Simulation. International Journal of Statistics and Probability, 1, 20-34.
- 31. Abu-Shal, T.A. and AL-Zaydi, A.M. (2012) Prediction Based on Generalized Order Statistics from a Mixture of Rayleigh Distributions Using MCMC Algorithm. Open Journal of Statistics, 2, 356-367.
http://dx.doi.org/10.4236/ojs.2012.23044 - 32. Abu-Shal, T.A. (2013) On Bayesian Prediction of Future Median Generalized Order Statistics Using Doubly Censored Data from Type-I Generalized Logistic Model. Journal of Statistical and Econometric Methods, 2, 61-79.
- 33. Ahmad, A.A. and AL-Zaydi, A.M. (2013) Inferences under a Class of Finite Mixture Distributions Based on Generalized Order Statistics. Open Journal of Statistics, 3, 231-244.
http://dx.doi.org/10.4236/ojs.2013.34027 - 34. Everitt, B.S. and Hand, D.J. (1981) Finite Mixture Distributions. Springer Netherlands, Dordrecht.
http://dx.doi.org/10.1007/978-94-009-5897-5 - 35. Titterington, D.M., Smith, A.F.M. and Makov, U.E. (1985) Statistical Analysis of Finite Mixture Distributions. John Wiley and Sons, New York.
- 36. McLachlan, G.J. and Basford, K.E. (1988) Mixture Models: Inferences and Applications to Clustering. Marcel Dekker, New York.
- 37. Teicher, H. (1963) Identifiability of Finite Mixtures. The Annals of Mathematical Statistics, 34, 1265-1269.
http://dx.doi.org/10.1214/aoms/1177703862 - 38. AL-Hussaini, E.K. and Ahmad, K.E. (1981) On the Identifiability of Finite Mixtures of Distributions. IEEE Transactions on Information Theory, 27, 664-668.
http://dx.doi.org/10.1109/TIT.1981.1056389 - 39. Ahmad, K.E. (1988) Identifiability of Finite Mixtures Using a New Transform. Annals of the Institute of Statistical Mathematics, 40, 261-265.
http://dx.doi.org/10.1007/BF00052342 - 40. AL-Hussaini, E.K., Al-Dayian, G.R. and Adham, S.A. (2000) On Finite Mixture of Two-Component Gompertz Lifetime Model. Journal of Statistical Computation and Simulation, 67, 1-20.




























