Open Journal of Statistics
Vol.05 No.04(2015), Article ID:57504,9 pages
10.4236/ojs.2015.54035
More on the Preliminary Test Stochastic Restricted Liu Estimator in Linear Regression Model
Sivarajah Arumairajan1,2, Pushpakanthie Wijekoon3
1Postgraduate Institute of Science, University of Peradeniya, Peradeniya, Sri Lanka
2Department of Mathematics and Statistics, Faculty of Science, University of Jaffna, Jaffna, Sri Lanka
3Department of Statistics & Computer Science, Faculty of Science, University of Peradeniya, Peradeniya, Sri Lanka
Email: arumais@gmail.com, pushpaw@pdn.ac.lk
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 May 2015; accepted 23 June 2015; published 29 June 2015
ABSTRACT
In this paper we compare recently developed preliminary test estimator called Preliminary Test Stochastic Restricted Liu Estimator (PTSRLE) with Ordinary Least Square Estimator (OLSE) and Mixed Estimator (ME) in the Mean Square Error Matrix (MSEM) sense for the two cases in which the stochastic restrictions are correct and not correct. Finally a numerical example and a Monte Carlo simulation study are done to illustrate the theoretical findings.
Keywords:
Multicollinearity, Stochastic Restrictions, Ordinary Least Square Estimator, Mixed Estimator, Preliminary Test Estimator, Mean Square Error Matrix

1. Introduction
To overcome the multicollinearity problem arises in the Ordinary Least Squares Estimation (OLSE) procedure, different methods have been proposed in the literature. One of the most important estimation methods is to consider biased estimators, such as the Ridge Estimator (RE) by Hoerl and Kennard [1] , the Liu Estimator (LE) by Liu [2] , and the Almost Unbiased Liu Estimator (AULE) by Akdeniz and Kaçiranlar [3] . Alternative method to solve the multicollinearity problem is to consider parameter estimation with some restrictions on the unknown parameters, which may be exact or stochastic. When the stochastic restrictions are available in addition to sample model, Theil and Goldberger [4] introduced the Mixed Estimator (ME). Replacing OLSE by ME in the Liu Estimator, the Stochastic Restricted Liu Estimator (SRLE) has been proposed by Hubert and Wijekoon [5] . When different estimators are available, the preliminary test estimation procedure is adopted to select a suitable estimator, and it can also be used as another estimator with combining properties of both estimators. The preliminary test approach was first proposed by Bancroft [6] , and then has been studied by many researchers, such as Judge and Bock [7] , Wijekoon [8] and Arumairajan and Wijekoon [9] . By combining OLSE and ME, the Ordinary Stochastic Preliminary Test Estimator (OSPE) was proposed by Wijekoon [8] . Recently, Arumairajan and Wijekoon [9] introduced the Preliminary Test Stochastic Restricted Liu Estimator (PTSRLE) by combining the Stochastic Restricted Liu Estimator and Liu Estimator. In their study, they compared PTSRLE with SRLE by using the Mean Square Error Matrix (MSEM) and Scalar Mean Square Error (SMSE) criterions.
In this research we further compare the mean square error matrix of PTSRLE with OLSE and ME. The rest of the paper is organized as follows. The model specification and estimation are given in section 2. In section 3, the mean square error matrix comparisons between PTSRLE with OLSE and ME are performed. A numerical example and a Monte Carlo simulation are used to illustrate the theoretical findings in section 4, and in section 5 we state the conclusions.
2. Model Specification and Estimation
First we consider the multiple linear regression model
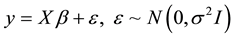 , (1)
, (1)
where y is an n × 1 observable random vector, X is an n × p known design matrix of rank p, β is a p × 1 vector of unknown parameters and ε is an n × 1 vector of disturbances.
In addition to sample model (1), let us be given some prior information about β in the form of a set of m independent stochastic linear restrictions as follows;
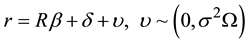 (2)
(2)
where r is an m × 1 stochastic known vector R is a m × p of full row rank  with known elements,
with known elements, 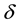 is non zero m × 1 unknown vector and υ is an m × 1 random vector of disturbances and
is non zero m × 1 unknown vector and υ is an m × 1 random vector of disturbances and 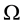 is assumed to be known and positive definite. Further it is assumed that υ is stochastically independent of ε. i.e.
is assumed to be known and positive definite. Further it is assumed that υ is stochastically independent of ε. i.e. .
.
The Ordinary Least Squares Estimator (OLSE) for model (1) and the Mixed Estimator (ME) (Theil and Goldberger [4] ) due to a stochastic prior restriction (2) are given by
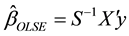 (3)
(3)
and
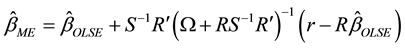 (4)
(4)
respectively, where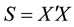 .
.
The expectation vector, and the mean square error matrix of  are given as
are given as
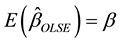 (5)
(5)
and
 (6)
(6)
respectively.
The expectation vector, dispersion matrix, and the mean square error matrix of 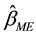 are given as
are given as
 , (7)
, (7)
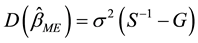 (8)
(8)
and
 (9)
(9)
respectively, where, 



The Liu Estimator (Liu, [2] ) is given as

Replacing OLSE by ME in the Liu Estimator, Hubert and Wijekoon [5] introduced the Stochastic Restricted Liu Estimator (SRLE), and is given by

when different estimators are available for the same parameter vector 


where 

Mean Square Error of 

For two given estimators 




Let us now turn to the question of the statistical evaluation of the compatibility of sample and stochastic information. The classical procedures is to test the hypothesis

under linear model (1) and stochastic prior information (2).
The Ordinary Stochastic Preliminary Test Estimator (OSPE) of 

Further, we can write (15) as

where,

which has a non-central 


and 


scripted interval, and zero otherwise. 

The expectation vector, dispersion matrix, and the mean square error matrix of 


an

respectively, where,
Recently, Arumairajan and Wijekoon [9] proposed the Preliminary Test Stochastic Restricted Liu Estimator (PTSRLE) by combining the Liu Estimator and Stochastic Restricted Liu Estimator, and is given by

Note that the PTSRLE can be rewritten as follows:

By using Equations (19), (20) and (21), Arumairajan and Wijekoon [9] derived the expectation vector, bias vector, dispersion matrix and mean square error matrix of PTSRLE as follows:



and

respectively, where
3. Mean Square Error Matrix Comparisons
In this section we compare the PTSRLE with OLSE and ME in the mean square error matrix sense for the two cases in which the stochastic restrictions are correct and not correct.
3.1. Comparison between the PTSRLE and OLSE
The mean square error matrix difference between OLSE and PTSRLE can be written as

where,
with


Now the following theorem can be stated
Theorem 1:
1) When the stochastic restrictions are true (i.e.






2) When the stochastic restrictions are not true (i.e.


Proof:
1) If stochastic restrictions are correct then

To apply lemma 2 (Appendix), we have to show that

Since 

Hence 







2) If stochastic restrictions are not correct then





We have already proved that







mum eigenvalue of


3.2. Comparison between the PTSRLE and ME
The mean square error matrix difference between ME and PTSRLE is

where 




Now we can give the following theorem.
Theorem 2:
1) When the stochastic restrictions are true (i.e.





2) When the stochastic restrictions are not true (i.e.


Proof:
1) When stochastic restrictions are true then






2) When stochastic restrictions are not true (i.e.






According to theorem 1 and 2 it is clear that PTSRLE is superior to OLSE and ME under certain conditions.
4. Numerical Illustrations
In this section the comparison of PTSRLE with OLSE and ME are demonstrated using a numerical example, and a simulation study.
4.1. Numerical Example
To illustrate our theoretical result, we consider the data set on Total National Research and Development Expenditures as a percent of Gross National product due to Gruber [10] . This data set is used by Akdeniz and Erol [11] , Li and Yang [12] and Wu and Yang [13] to verify the theoretical results. Data shows Total National Research and Development Expenditures as a Percent of Gross National Product by Country: 1972-1986. It represents the relationship between the dependent variable y the percentage spent by the United States and the four other independent variables 





The four column of the 10 × 4 matrix X comprise the data on 

1) The eigen values of
2) The OLS estimator of
3) The OLS estimator of
4) The condition number of
The condition number implies the existence of multicollinearity in the data set. We consider the following stochastic restrictions (Li and Yang, [12] )

Further the significance level is taken as α = 0.05. Figure 1 is drawn by using the SMSE obtained by using Equations (6), (9) and (27).
Based on Figure 1, we can say that the SMSE of PTSRLE is larger than the SMSE of both ME and OLSE when d is small. But the PTSRLE has the smallest SMSE than both ME and OLSE for
4.2. Monte Carlo Simulation
To illustrate the behavior of our proposed estimators, we perform the Monte Carlo Simulation study by considering different levels of multicollinearity. Following McDonald and Galarneau [14] we generate explanatory variables as follows:
where 


where 






According to Figure 2, the PTSRLE has the smallest SMSE than ME except d is small. However the OLSE has the smallest SMSE than ME and PTSRLE. From Figure 3, the SMSE of PTSRLE is larger than the SMSE of both OLSE and ME when d is small. From Figure 4 and Figure 5, we can notice that most of the cases, the PTSRLE has the smallest SMSE than ME and OLSE.
5. Conclusion
In this paper we have shown that the Preliminary Test Stochastic Restricted Liu Estimator is superior to Mixed Estimator and Ordinary Least Square Estimator in the mean square error matrix sense under certain conditions.
Figure 1. Estimated SMSE for PTSRLE, ME and OLSE.
Figure 2. Estimated SMSE for PTSRLE, ME and OLSE when γ = 0.9.
Figure 3. Estimated SMSE for PTSRLE, ME and OLSE when γ = 0.99.
Figure 4. Estimated SMSE for PTSRLE, ME and OLSE when γ = 0.999.
Figure 5. Estimated SMSE for PTSRLE, ME and OLSE when γ = 0.9999.
From the simulation study and the numerical illustration we notice that the PTSRLE has the smallest SMSE than ME and OLSE when multicollinearity among the predictor variables is large.
Acknowledgements
We thank the Postgraduate Institute of Science, University of Peradeniya, Sri Lanka for providing all facilities to do this research.
Cite this paper
SivarajahArumairajan,PushpakanthieWijekoon,11, (2015) More on the Preliminary Test Stochastic Restricted Liu Estimator in Linear Regression Model. Open Journal of Statistics,05,340-349. doi: 10.4236/ojs.2015.54035
References
- 1. Hoerl, E. and Kennard, W. (1970) Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics, 12, 55-67.
http://dx.doi.org/10.1080/00401706.1970.10488634 - 2. Liu, K. (1993) A New Class of Biased Estimate in Linear Regression. Communications in Statistics—Theory and Methods, 22, 393-402.
http://dx.doi.org/10.1080/03610929308831027 - 3. Akdeniz, F. and Kaçiranlar, S. (1995) On the almost Unbiased Generalized Liu Estimator and Unbiased Estimation of the Bias and MSE. Communications in Statistics—Theory and Methods, 34, 1789-1797.
http://dx.doi.org/10.1080/03610929508831585 - 4. Theil, H. and Goldberger. A.S. (1961) On Pure and Mixed Estimation in Economics. International Economic Review, 2, 65-77.
http://dx.doi.org/10.2307/2525589 - 5. Hubert, M.H. and Wijekoon, P. (2006) Improvement of the Liu Estimator in Linear Regression Model. Statistical Papers, 47, 471-479.
http://dx.doi.org/10.1007/s00362-006-0300-4 - 6. Bancroft, A. (1944) On Biases in Estimation Due to Use of Preliminary Tests of Significance. Annals of Mathematical Statistics, 15, 190-204.
http://dx.doi.org/10.1214/aoms/1177731284 - 7. Judge, G. and Bock, E. (1978) The Statistical Implications of Pre-Test and Stein-Rule Estimators in Econometrics. North Holland, New York.
- 8. Wijekoon, P. (1990) Mixed Estimation and Preliminary Test Estimation in the Linear Regression Model. Ph.D. Thesis, University of Dortmund, Dortmund.
- 9. Arumairajan, S. and Wijekoon, P. (2013) Improvement of the Preliminary Test Estimator When Stochastic Restrictions are Available in Linear Regression Model. Open Journal of Statistics, 3, 283-292.
http://dx.doi.org/10.4236/ojs.2013.34033 - 10. Gruber. M.H.J. (1998) Improving Efficiency by Shrinkage: The James-Stein and Ridge Regression Estimators. Dekker, Inc., New York.
- 11. Akdeniz, F. and Erol, H. (2003) Mean Squared Error Matrix Comparisons of Some Biased Estimators in Linear Regression. Communications in Statistics—Theory and Methods, 32, 2389-2413.
http://dx.doi.org/10.1081/STA-120025385 - 12. Li, Y. and Yang, H. (2010) A New Stochastic Mixed Ridge Estimator in Linear Regression. Statistical Papers, 51, 315-323.
http://dx.doi.org/10.1007/s00362-008-0169-5 - 13. Wu, J. and Yang, H. (2013) Two Stochastic Restricted Principal Components Regression Estimator in Linear Regression. Communications in Statistics—Theory and Methods, 42, 3793-3804.
http://dx.doi.org/10.1080/03610926.2011.639004 - 14. McDonald, C. and Galarneau, A. (1975) A Monte Carlo Evaluation of some Ridge-Type Estimators. Journal of American Statistical Association, 70, 407-416.
http://dx.doi.org/10.1080/01621459.1975.10479882 - 15. Newhouse, J.P. and Oman, S.D. (1971) An Evaluation of Ridge Estimators. Rand Report, No. R-716-Pr, 1-28.
- 16. Rao, C.R. and Touterburg, H. (1995) Linear Models, Least Squares and Alternatives. Springer Verlag, Berlin.
http://dx.doi.org/10.1007/978-1-4899-0024-1 - 17. Farebrother, R.W. (1976) Further Results on the Mean Square Error of Ridge Regression. Journal of the Royal Statistical Society, 38, 248-250.
- 18. Wang, S.G., Wu, M.X. and Jia, Z.Z. (2006) Matrix Inequalities. 2nd Edition, Chinese Science Press, Beijing.
- 19. Trenkler, G. and Toutenburg, H. (1990) Mean Square Error Matrix Comparisons between Biased Estimators—An Overview of Recent Results. Statistical Papers, 31, 165-179.
http://dx.doi.org/10.1007/BF02924687
Appendix
Lemma 1: (Rao and Touterburg, [16] )
Let A and B be (n × n) matrices such that A > 0 and

Lemma 2: (Farebrother, [17] )
Let A > 0 be an (n × n) matrix, b an (n × 1) vector. Then 

Lemma 3: (Wang et al., [18] )
Let n × n matrices M > 0, N > 0 (or



Lemma 4: (Trenkler and Toutenburg, [19] )
Let 


















