Open Journal of Statistics
Vol.04 No.09(2014), Article ID:50921,10 pages
10.4236/ojs.2014.49072
A Co-Evolution Model for Dynamic Social Network and Behavior
Liping Tong*, David Shoham, Richard S. Cooper
Department of Public Health Sciences, Loyola University Medical School, Maywood, USA
Email: *ltong@luc.edu, dshoham@luc.edu, rcooper@luc.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 August 2014; revised 15 September 2014; accepted 28 September 2014
ABSTRACT
Individual behaviors, such as drinking, smoking, screen time, and physical activity, can be strongly influenced by the behavior of friends. At the same time, the choice of friends can be influenced by shared behavioral preferences. The actor-based stochastic models (ABSM) are developed to study the interdependence of social networks and behavior. These methods are efficient and useful for analysis of discrete behaviors, such as drinking and smoking; however, since the behavior evolution function is in an exponential format, the ABSM can generate inconsistent and unrealistic results when the behavior variable is continuous or has a large range, such as hours of television watched or body mass index. To more realistically model continuous behavior variables, we propose a co-evolution process based on a linear model which is consistent over time and has an intuitive interpretation. In the simulation study, we applied the expectation maximization (EM) and Markov chain Monte Carlo (MCMC) algorithms to find the maximum likelihood estimate (MLE) of parameter values. Additionally, we show that our assumptions are reasonable using data from the National Longitudinal Study of Adolescent Health (Add Health).
Keywords:
Social Network, Social Behavior, Co-Evolution, Markov Chain, Stationary Distribution

1. Introduction
Numerous studies have examined the role friends play in influencing behavior. Researchers have made exten- sive use of data from the Framingham Heart Study-Network Study (FHS-Net) [1] -[3] , the National Longi- tudinal Study of Adolescent Health (Add Health) [4] [5] , and other datasets [6] - [9] to examine whether health behaviors such as smoking and becoming obese can spread between friends. However, the validity of analyses based on observational studies has been called into question by several authors [10] [11] . The main concern is the impossibility of identification of peer influence from peer selection using regression-based approaches [11] .
In response to these concerns, the actor-based stochastic model (ABSM) was proposed by [12] [13] . This model employs Markov chain simulation and method-of-moments (MOM) to adjust estimates of peer influence and peer selection parameters using longitudinal data. The underlying model is a random utility function, where the utilities are not observed. This type of model is the most appropriate for scenarios where an actor must make a single choice from a given set of choices [14] , although several researchers have applied the ABSM model to continuous behaviors [7] [8] .
In ABSM, a continuous time finite-state-space Markov process was used to model the dynamic relationship between social network and behaviors. Three steps describe this process. The first step determines when the chance for the next change will occur. Let 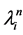 be the rate of change for actor
be the rate of change for actor ’s network and
’s network and  be the rate of change for actor
be the rate of change for actor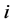 ’s behavior. Then the waiting time for the next chance of change is exponentially distri-
’s behavior. Then the waiting time for the next chance of change is exponentially distri-
buted with parameter 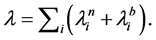 Note that the chance of change does not necessarily results in success-
Note that the chance of change does not necessarily results in success-
ful change. The second step defines which actor has the opportunity to make a change (either a network change or a behavior change). The probability of a network change taken by a particular actor 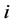 is given by
is given by 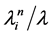 and the probability that this is a behavior change taken by actor
and the probability that this is a behavior change taken by actor 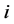 is
is  At the third step there is an opportunity to make a change in network or behavior. If actor i is making a network change, there are n possible outcomes, where
At the third step there is an opportunity to make a change in network or behavior. If actor i is making a network change, there are n possible outcomes, where 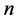 is the number of actors in the network. This condition holds because for network changes, at most one tie difference from the current network is allowed; no network change is also allowed. Say,
is the number of actors in the network. This condition holds because for network changes, at most one tie difference from the current network is allowed; no network change is also allowed. Say,  is the current network. The next network
is the current network. The next network 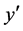 must be either equal to
must be either equal to 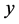 or deviate from
or deviate from 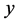 exactly one element in row
exactly one element in row . To simplify notation, for adjacent matrix
. To simplify notation, for adjacent matrix 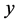 and indicators
and indicators 


























from data (in a analysis), and 



If actor 

















evolution. Then the behavior objective function of actor i is 
actor 


In summary, the probability to change to a new set of value 

To use ABSM, the behavior variable must be bounded and discretized. For continuous behavior variables, such as body mass index (BMI), time spent watching television, etc., the process of discretizing can be arbitrary and tricky. In Section 3 (Results), we show that the effect of average BMI similarity can be very different for integer and categorical BMI.
Based on the above considerations, we were motivated to develop a linear-based behavior evolution model. In our model, the network evolution is similar to ABSM. However, the behavior evolution is defined by a continuous Markov process, which is completely different from [12] [13] . To simplify computation, we consider only a real network change as an “event” (instead of the opportunity of change). In addition, for behavior evolution, we assume normal residuals for values of change.
2. Methods
2.1. Complete and Observed Data
For illustration purpose, consider two waves of data that are collected at time 0 and T. The complete data during time period 



write as






Here the observed data are represented in black ovals, missing behavior data in blue ovals, and missing network data in red ovals. The network evolution process is represented by red arrows and behavior variable by blue arrows.
2.2. Occurrence of Events
The number of events 





For now, we assume the chance of making a network change is the same for each actor. This assumption can be extended to be actor-specific if the data are informative enough.
2.3. Network Evolution
Let 





that the edge


before the next event is


2.4. Behavior Evolution
Define


where 





from each other or any other random variable, and 




Note that when




Since behavior variables are accumulated over time, we would expect that when modeling behaviors, the distribution of change from time 





where 





2.5. An Example Choice of W
As an example, assume that the 


where 

where

havior variables 


2.6. Complete Data Log-Likelihood Function
Exponential random graph models (ERGMs) are commonly employed to test whether the presence of network ties (edges) differs from what would be expected in a random graph, given some set of network statistics [15] . In the ERGM, the parameters are 



where
2.7. EM Algorithm to Find MLE of Parameters
Parameter 







function using simulated samples and obtain

MLE of parameters 



2.8. Normal Distribution to Simulate Behavior Variable Zu
In the general multi-dimensional situation, assume that






with mean 


and
Here 











according to the normal distribution with mean 

2.9. Sample Hidden Variables Conditional on Observed Data
Remember that the observed data are 













· Sample k: let d be the number of edges 


¾ If d is even,
¾ If d is odd,
· Sample 


· Sample 
1) Sample 






and evaluate the density function of the above normal distribution at the realized value

2) Sample 



a) Define the important list to be


b) If



¾ If




¾ If






c) If







d) Denote the probability from the situlation of 


3) Likewise, sequentially sample




4) Use the Metropolis Hastings algorithm to decide whether to accept the generated sample 
where 
3. Results
We used the Add Health “saturation sample” data to check the reasonableness of our assumptions and to per- form simulation studies. First, we show results based on the ABSM model; next we compare these results with our co-evolution model.
The Add Health saturation sample data are based on adolescents in 16 high schools where all students in a given school were asked to participate. There are two waves (1 year apart) of friendship network data, including environmental variables and self-reported height/weight. We focus on one school called “Jefferson High” as in [16] [17] , where over 99% students are white. In this data set, the sample size with complete data over two waves is 624, among which 52.7% are males. The grade levels range from 9 to 11, the average BMI is 23.1 with SD being 4.4 and the average outdegree (number of friends named) of the network is 4.0 with SD being 2.1.
3.1. Results for ABSM Models
The results based on ABSM are in Table 1. The parameter of waiting time for the opportunity of change is

The estimated network objective function is
where 


For example, consider the behavior evolution for individuals who have no friends. The estimated behavior objective function becomes
The probabilities for BMI evolution are shown in Table 2. The results indicate that for individuals whose BMI is greater than 17.5 there is a higher probability of an increase in BMI, which is consistent with the ob- served propensity for BMI to “track” over time [18] [19] . However, for individuals whose BMI is less than 17.5, the results indicate a higher probability of decrease in BMI; this may not be reasonable.
3.2. Validation of Assumptions in the Joint Evolution Model
Using the Add Health data for the school of Jefferson High, we can draw the histogram of BMI change and
Table 1. Estimated ABSM for the school of Jefferson High.
Table 2. BMI evolution probabilities for individuals with no friends.
screen time change between these two waves (Figure 1). From Figure 1, we see that the normality assumption is not perfectly satisfied due to larger amount of observations around zero. However, the distributions are approximately symmetric, which is usually sufficient in a linear model if sample size is moderately large (for example, greater than 30).
We also draw the scatter plot of individual’s BMI change versus average friends’ BMI change to check lin- earity assumption. The plot in Figure 2 suggest weak linear relationship between these two variables. Note that to draw this plot, we consider only friends who were nominated at both waves so that the BMI change com- parison is valid. Therefore, the relationship shown reflect only part of the data, which contributes to the weak- ened linear relationship. These findings suggest that our assumptions are approximately satisfied.
3.3. Simulation Study
To simulate a realistic network with reasonable BMI values assigned to each individual, we randomly sampled 30 individuals (from the same school) in the Add Health data. The average BMI of selected individuals is
We specified that network and BMI would evolve for 60 days using the following parameters values:




Apply the EM procedure described in Methods section, we obtained the following parameter estimations (Table 3). From the table, we see that some of the parameter estimates, such as event rate



The explanation of the above parameters are mostly straight forward. For example, the rate of events 


3.4. Application to Real Data
Since our model cannot deal with a network as large as 624 individuals, we include only students in grade 11 in this application. The sample size here is 110. We first run the ABSM model using RSiena (Table 4). Then we fit in our joint co-evolution model (Table 5).
Compare results from Table 4 and Table 5. We found out that the results for network evolution are similar from both models. This is because we are using the same network evolution models. The different behavior models have only limited effect on the network evolution process. Both model suggest that there is no effect of selection or influence. That is, similarity in BMI does not affect the process of making friends; an individual’s friends’ BMI change does not affect his/her own BMI. Note that when we use the complete data of 624 indivi-
Figure 1. The histogram of BMI change for the school of Jeffer- son High in Add Health data.
Figure 2. The scatter plot of individuals’ BMI change versus average friends’ BMI change for the school of Jefferson High in Add Health data.
Table 3. MLE parameter estimations using simulated data.
duals, we got significant effect of selection 

4. Discussion
We have developed a joint social network and behavior evolution model. In our model, behavior changes are
Table 4. Estimated ABSM using Jefferson High grade 11 data.
Table 5. MLE parameter estimations using Jefferson High grade 11 data.
consistent over time. That is, 

The field of social network analysis is a relatively young field. However, useful contributions are being made today. The range of applications is vast, from the contagion of health behaviors described in this paper [20] , to the study of group formations in human societies [21] . Further advances will require improved statistical methods (to deal with different types of behaviors departing from the discrete choice model), as well as more extensive empirical data sets incorporating social networks. Many future studies will use continuous outcome measures; we hope the method presented here will be valuable in extending the ABSM to such outcomes.
Our model does require intensive computation. However, we are confident that more efficient algorithms can be developed. Though our model requires specific assumptions, we have demonstrated that these assumptions are reasonably easy to satisfy using real data. Sensitivity analysis will ultimately be required to determine if our model works well when some of the assumptions are violated.
References
- Christakis, N.A. and Fowler, J.H. (2007) The Spread of Obesity in a Large Social Network over 32 Years. New England Journal of Medicine, 357, 370-379. http://dx.doi.org/10.1056/NEJMsa066082
- Fowler, J.H. and Christakis, N.A. (2008) Dynamic Spread of Happiness in a Large Social Network: Longitudinal Analysis over 20 Years in the Framingham Heart Study. British Medical Journal, 337, 1-9. http://dx.doi.org/10.1136/bmj.a2338
- Fowler, J.H. and Christakis, N.A. (2008) Estimating Peer Effects on Health in Social Networks: A Response to Cohen-Cole and Fletcher; and Trogdon, Nonnemaker, and Pais. Journal of Health Economics, 27, 1400-1405. http://dx.doi.org/10.1016/j.jhealeco.2008.07.001
- Alexander, C., Piazza, M., Mekos, D. and Valente, T. (2001) Peers Schools and Adolescent Cigarette Smoking. Journal of Adolescent Health, 29, 22-30. http://dx.doi.org/10.1016/S1054-139X(01)00210-5
- Trogdon, J.G., Finkelstein, E.A., Hylands, T., Dellea, P.S. and Kamal-Bahl, S.J. (2008) Indirect Costs of Obesity: A Review of the Current Literature. Obesity Reviews, 9, 489-500. http://dx.doi.org/10.1111/j.1467-789X.2008.00472.x
- De La Haye, K., Robins, G., Mohr, P. and Wilson, C. (2010) Obesity-Related Behaviors in Adolescent Friendship Networks. Social Networks, 32, 161-167. http://dx.doi.org/10.1016/j.socnet.2009.09.001
- De La Haye, K., Robins, G., Mohr, P. and Wilson, C. (2011) How Physical Activity Shapes, and Is Shaped by, Adolescent Friendships. Social Science & Medicine, 73, 719-728. http://dx.doi.org/10.1016/j.socscimed.2011.06.023
- De La Haye, K., Robins, G., Mohr, P. and Wilson, C. (2011) Homophily and Contagion as Explanations for Weight Similarities among Adolescent Friends. Journal of Adolescent Health, 49, 421-427. http://dx.doi.org/10.1016/j.jadohealth.2011.02.008
- Salvy, S.J., De La Haye, K., Bowker, J.C. and Hermans, R.C.J. (2012) Influence of Peers and Friends on Children’s and Adolescents’ Eating and Activity Behaviors. Physiology & Behavior, 106, 369-378. http://dx.doi.org/10.1016/j.physbeh.2012.03.022
- Cohen-Cole, E. and Fletcher, J.M. (2008) Is Obesity Contagious? Social Network vs. Environmental Factors in the Obesity Epidemic. Journal of Health Economics, 27, 1382-1387. http://dx.doi.org/10.1016/j.jhealeco.2008.04.005
- Shalizi, C. and Thomas, A. (2011) Homophily and Contagion Are Generically Confounded in Observational Social Network Studies. Sociological Methods and Research, 40, 211-239. http://dx.doi.org/10.1177/0049124111404820
- Snijders, T.A.B., Pattison, P.E., Robins, G.L. and Handcock, M.S. (2006) New Specifications for Exponential Random Graph Models. Sociological Methodology, 36, 99-153. http://dx.doi.org/10.1111/j.1467-9531.2006.00176.x
- Snijders, T.A.B., van de Bunt, G.G. and Steglich, C.E.G. (2010) Introduction to Actor-Based Models for Network Dynamics. Social Networks, 32, 44-60. http://dx.doi.org/10.1016/j.socnet.2009.02.004
- Train, K. (2009) Discrete Choice Methods with Simulation. Cambridge University Press, New York. http://dx.doi.org/10.1017/CBO9780511805271
- Robins, G., Pattison, P., Kalish, Y. and Lusher, D. (2007) An Introduction to Exponential Random Graph (p*) Models for Social Networks. Social Networks, 29, 173-191. http://dx.doi.org/10.1016/j.socnet.2006.08.002
- Bearman, P.S. and Moody, J. (2004) Suicide and Friendships among American Adolescents. American Journal of Public Health, 94, 89-95. http://dx.doi.org/10.2105/AJPH.94.1.89
- Bearman, P.S., Moody, J. and Stovel, K. (2004) Chains of Affection: The Structure of Adolescent Romantic and Sexual Networks. American Journal of Sociology, 110, 44-91. http://dx.doi.org/10.1086/386272
- Gordon-Larsen, P., The, N.S. and Adair, L.S. (2010) Longitudinal Trends in Obesity in the United States from Adolescence to the Third Decade of Life. Obesity, 18, 1801-1804. http://dx.doi.org/10.1038/oby.2009.451
- Wright, C.M., Emmett, P.M., Ness, A.R., et al. (2010) Tracking of Obesity and Body Fatness through Mid-Childhood. Archives of Disease in Childhood, 95, 612-617. http://dx.doi.org/10.1136/adc.2009.164491
- Smith, K.P. and Christakis, N.A. (2008) Social Networks and Health. Annual Review of Sociology, 34, 405-429. http://dx.doi.org/10.1146/annurev.soc.34.040507.134601
- Apicella, C.L., Marlowe, F.W., et al. (2012) Social Networks and Cooperation in Hunter-Gatherers. Nature, 481, 497- 501. http://dx.doi.org/10.1038/nature10736
NOTES
*Corresponding author.





















