Open Journal of Statistics
Vol.05 No.01(2015), Article ID:54307,5 pages
10.4236/ojs.2015.51011
Comparison of Uniform and Kernel Gaussian Weight Matrix in Generalized Spatial Panel Data Model
Tuti Purwaningsih, Erfiani, Anik Djuraidah
Departement of Statistics, Graduate School of Bogor Agricultural University, Bogor, Indonesia
Email: purwaningsiht@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 February 2015; accepted 25 February 2015; published 28 February 2015
ABSTRACT
Panel data combine cross-section data and time series data. If the cross-section is locations, there is a need to check the correlation among locations. ρ and λ are parameters in generalized spatial model to cover effect of correlation between locations. Value of ρ or λ will influence the goodness of fit model, so it is important to make parameter estimation. The effect of another location is covered by making contiguity matrix until it gets spatial weighted matrix (W). There are some types of W―uniform W, binary W, kernel Gaussian W and some W from real case of economics condition or transportation condition from locations. This study is aimed to compare uniform W and kernel Gaussian W in spatial panel data model using RMSE value. The result of analysis showed that uniform weight had RMSE value less than kernel Gaussian model. Uniform W had stabil value for all the combinations.
Keywords:
Component, Uniform Weight, Kernel Gaussian Weight, Generalized Spatial Panel Data Model

1. Introduction
Panel data analysis combines cross-section data and time series data, in sampling when the data are taken from different locations. It’s commonly found that the observation value at one location depends on observation value in another location. In the other name, there is spatial correlation between the observations, which is spatial dependence. Spatial dependence in this study is covered by generalized spatial model which is focussed on dependence between locations and errors [1] . If there is spatial influence but not involved in model so error assumption that between observations must be independent will not fulfilled. So the model will be in bad condition, for that need, a model that involves spatial influence in the analysis panel data will be mentioned as Spatial Panel Data Model.
Some recent literature of spatial cross-section data is Spatial Ordinal Logistic Regression by Aidi and Purwaningsih [2] , and Geographically Weighted Regression [3] . Some of the recent literature of Spatial Panel Data is forecasting with spatial panel data [3] and spatial panel models [4] . For accomodating spatial dependence in the model, there is spatial weighted matrix 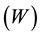 that is an important component to calculate the spatial correlation between locations. Spatial parameter in generalized spatial panel data model, is known as
that is an important component to calculate the spatial correlation between locations. Spatial parameter in generalized spatial panel data model, is known as 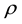 or
or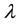 . There are some types of
. There are some types of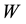 ―uniform
―uniform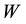 , binary
, binary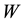 , inverse distance
, inverse distance 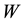 and some
and some 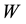 from real cases of economics condition or transportation condition from the area. This research is aimed to compare uniform
from real cases of economics condition or transportation condition from the area. This research is aimed to compare uniform 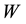 and kernel Gaussian
and kernel Gaussian 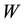 in generalized spatial panel data model using RMSE value which is obtained from simulation.
in generalized spatial panel data model using RMSE value which is obtained from simulation.
2. Literature Review
2.1. Data Panel Analysis
Data used in the panel data modelisa combination of cross section and time-series data. Crossection data is data collected at one time of many units of observation, then time-series data is data collected over time to an observation. If each unit has a number of observations a cross individuals in the same period of time series, it is calleda balanced panel data. Conversely, if each individual unit has a number of observations a cross different period of time series, it is called an unbalanced panel data (unbalanced panel data).
In general, panel data regression model is expressed as follows:
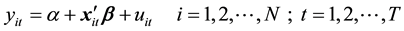 (1)
(1)
with 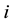 is an index for crossection data and t is index of time series.
is an index for crossection data and t is index of time series. 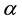 is a constant value,
is a constant value,  is a vector of size
is a vector of size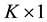 , with
, with 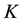 specifies the number of explanatory variables. Then
specifies the number of explanatory variables. Then 



Residual components of the direction of the regression model in Equation (1) can be defined as follows:

where 

2.2. Spatial Weighted Matrix (W)
Spatial weighted matrix is basically a matrix that describes the relationship between regions and obtained by distance or neighbourhood information. Diagonal of the matrix is generally filled with zero value. Since the weighting matrix shows the relationship between the overall observation, the dimension of this matrix is N × N [6] . There are several approaches that can be done to show the spatial relationship between the location, including the concept of intersection (contiguity). There are three types of intersection, namely Rook Contiguity, Bishinop Contiguity and Queen Contiguity [6] .
After determining the spatial weighting matrix to be used, further normalization in the spatial weighting matrix. In general, the matrix used for normalization normalization row (row-normalize). This means that the matrix is transformed so that the sum of each row of the matrix becomes equal to one. There are other alternatives in the normalization of this matrix is to normalize the columns of the matrix so that the sum of each column in the weighting matrix be equal to one. Also, it can also perform normalization by dividing the elements of the weighting matrix with the largest characteristic root of the matrix ( [6] [7] ).
There are several types of Spatial Weight










with 



2.3. Generalized Spatial Panel Data Model
Generalized spatial model expressed in the following equation:

where 



3. Methodology
Data used in this study was gotten from simulation using generalized spatial panel data model as Equation (5) with initiation of some parameter. Simulation was done use R program. The following step is used to generate the spatial data panel which is consist of index n and t. In dexnindicates the number of locations and indextindicates the number of period in each locations. Here is the proccess:
1) Determining the number of locations to be simulated is


2) Makes 3 types of map location on step 1.
3) Creating a binary spatial weighted matrix based on the concept of queen contiguity of each type of map locations. In this step, to map the 3 locations it will form a 3 × 3 matrix, 9 locations will form a 9 × 9 matrix and 25 locations form a 25 × 25 matrix.
4) Creating spatial uniform weighted matrix based on the concept of queen contiguity of each type of map locations.
5) Making weighted matrix kernel Gaussian based on the concept of distance. To make this matrix, previously researchers randomize the centroid points of each location. After setting centroid points, then measure the distance between centroids and used it as a reference to build kernel Gaussian W. Gaussian kernel W as follows:

6) Specifies the number of time periods to be simulated is



7) Generating the data 

8) Cronecker multiplication between matrix identtity of time periods and W, then get new matrix named IW.
9) Multiply matrix IW and 

10) Build a spatial panel data models and get the value of RMSE.
11) Repeat steps 7)-9) until 1000 replications for each combination on types of




Types of W: W binary, W uniform and Gaussian kernel W;
Types of
Types of
Types of

12) Get the RMSE value for all of 1000 replicationsoh each combination between W, 


13) Determine the best W based on the smallest RMSE for all combinations.
4. Results and Discussions
Simulation generate data for vector Y as dependent variable and X matrix as independent variable. Y and X is generate with parameter initiation. After doing simulation, we can get RMSE for each combinations and proccessing it, then we can calculate RMSE for each W, N, T, 

Table 1. Value of RMSE resulted from simulation for all the combinations (W, N, T, ρ and λ).
Figure 1. Comparison of RMSE between uniform W and kernel Gaussian W for all combinations.
Figure 2. Comparison RMSE each W for each parameter.
Based on Figure 1 can be said that uniform W has smaller RMSE than kernel Gaussian W for T = 12, T = 36 on location N = 3, then for T = 6, 12, 36 on location N = 25 and the remaining combinations, kernel Gaussian is higher. If we look the level of stabilization, uniform W is better than kernel Gaussian W. We can look ats the graph in blue line as uniform W, it has value only in range 1, 4 until 2 then kernel Gaussian W has range from 1 - 3. So can be concluded that uniform W is better than kernel Gaussian W.
Based on Figure 2, we can look that average RMSE of uniform W is smaller in





5. Conclusion
After looking at the result, it can be concluded that uniform W is better than kernel Gaussian W almost for all combinations of N and T. Then uniform W is better in 

Acknowledgements
The first, authors would like to thankful to Allah SWT, my parents, lecturer and all of friends. This research was supported by private funds.
References
- Anselin, L., Gallo, J. and Jayet, H. (2008) The Econometrics of Panel Data. Springer, Berlin.
- Aidi, M.N. and Purwaningsih, T. (2012) Modelling Spatial Ordinal Logistic Regression and the Principal Component to Predict Poverty Status of Districts in Java Island. International Journal of Statistics and Application, 3, 1-8.
- Fotheringham, A.S., Brunsdon, C. and Chartlon, M. (2002) Geographically Weighted Regression, the Analysis of Spatially Varying Relationships. John Wiley and Sons, Ltd., Hoboken.
- Elhorst, J.P. (2011) Spatial Panel Models. Regional Science and Urban Econometric.
- Baltagi, B.H. (2005) Econometrics Analysis of Panel Data. 3rd Edition, John Wiley and Sons, Ltd., England.
- Dubin, R. (2009) Spatial Weights. In: Fotheringham, A.S. and Rogerson, P.A., Eds., Handbook of Spatial Analysis, Sage Publications, London. http://dx.doi.org/10.4135/9780857020130.n8
- Elhorst, J.P. (2010) Spatial Panel Data Models. In: Fischer, M.M. and Getis, A., Eds., Handbook of Applied Spatial Analysis, Springer, New York. http://dx.doi.org/10.1007/978-3-642-03647-7_19




