Open Journal of Discrete Mathematics
Vol.3 No.3(2013), Article ID:34518,7 pages DOI:10.4236/ojdm.2013.33030
On Some Numbers Related to the Erdös-Szekeres Theorem
1Department of Mathematics, University of Idaho, Moscow City, Moscow
2Department of Mathematics, Washington State University, Pullman, USA
Email: markn@uidaho.edu
Copyright © 2013 Mark J. Nielsen, William Webb. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 15, 2013; revised February 16, 2013; accepted April 15, 2013
Keywords: Erdos-Szekeres Theorem; Combinatorial Geometry
ABSTRACT
A crossing family of segments is a collection of segments each pair of which crosses. Given positive integers  and
and , a
, a 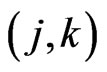 grid is the union of two pairwise-disjoint collections of segments (with
grid is the union of two pairwise-disjoint collections of segments (with 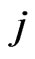 and
and 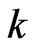 members, respectively) such that each segment in the first collection crosses all members of the other. Let
members, respectively) such that each segment in the first collection crosses all members of the other. Let 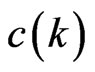 be the least integer such that any planar set of
be the least integer such that any planar set of  points in general position generates a crossing family of
points in general position generates a crossing family of  segments. Also let
segments. Also let 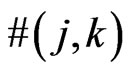 be the least integer such that any planar set of
be the least integer such that any planar set of 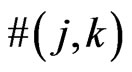 points in general position generates a
points in general position generates a 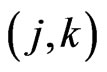 -grid. We establish here the facts
-grid. We establish here the facts 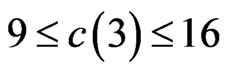 and
and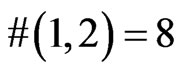 .
.
1. Introduction
For each positive integer  let
let 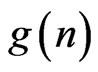 be the least integer such that every planar set of
be the least integer such that every planar set of 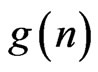 points in general position contains the vertices of some convex n-gon. This number was introduced by Erdös and Szekeres in 1935 (see [1] and [2]) who established the bounds
points in general position contains the vertices of some convex n-gon. This number was introduced by Erdös and Szekeres in 1935 (see [1] and [2]) who established the bounds 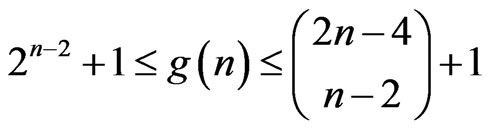 and conjectured that the lower bound is in fact an equality. The values
and conjectured that the lower bound is in fact an equality. The values 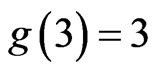 and
and 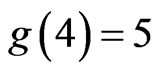 are easy, and several proofs of the fact
are easy, and several proofs of the fact 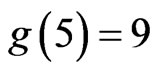 have been given. However, no other values have been computed exactly and the upper bound given by Erdös and Szekeres stood until recently as the best known. A seqence of 1998 papers by Chung and Graham [3], Kleitman and Pachter [4], and finally Tóth and Valtr [5] improved the above-mentioned bound to
have been given. However, no other values have been computed exactly and the upper bound given by Erdös and Szekeres stood until recently as the best known. A seqence of 1998 papers by Chung and Graham [3], Kleitman and Pachter [4], and finally Tóth and Valtr [5] improved the above-mentioned bound to
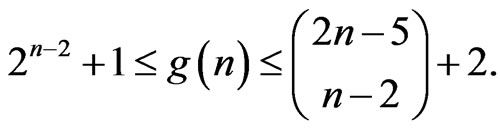 (0.1)
(0.1)
Morris and Soltan [6] provide an excellent survey of related results.
Given the apparent difficulty of determining values of 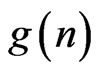 we might well seek weakened notions of these numbers. For example, let
we might well seek weakened notions of these numbers. For example, let 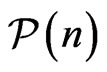 be a combinatorial property satisfied by the vertex set of a convex
be a combinatorial property satisfied by the vertex set of a convex 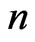 -gon. It might be interesting to ask how large a set
-gon. It might be interesting to ask how large a set 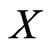 must be to guarantee the existence of a subset of
must be to guarantee the existence of a subset of 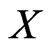 having property
having property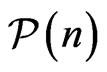 . We will consider such generalizations where the property
. We will consider such generalizations where the property 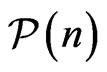 is a specified intersection behavior of some subset of the diagonals to a convex
is a specified intersection behavior of some subset of the diagonals to a convex  -gon.
-gon.
We will say that a set 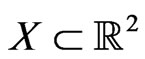 generates a collection
generates a collection 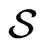 of segments if each segment in
of segments if each segment in  has its endpoints in
has its endpoints in . Also, we will say that a collection
. Also, we will say that a collection 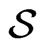 of segments is a crossing family if each pair of segments in
of segments is a crossing family if each pair of segments in 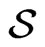 crosses (intersects at a point that is not endpoint to either segment). Now if
crosses (intersects at a point that is not endpoint to either segment). Now if 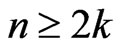 then the vertex set of a convex
then the vertex set of a convex 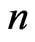 -gon clearly generates a crossing family of size
-gon clearly generates a crossing family of size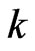 . Define
. Define 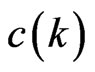 to be the least integer such that any planar set of
to be the least integer such that any planar set of 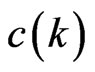 points in general position generates a crossing family of
points in general position generates a crossing family of 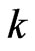 segments. Then as we have noted,
segments. Then as we have noted, 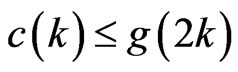 , but we might expect
, but we might expect 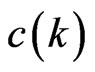 to be much less. Indeed, the main result in the paper by Aronov et al. [7] implies the much stronger bound
to be much less. Indeed, the main result in the paper by Aronov et al. [7] implies the much stronger bound
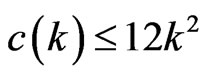 (0.2)
(0.2)
for these numbers. The authors of that paper ask whether this bound might be improved to a linear bound—a question that remains open at present.
Now let  and
and 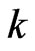 be positive integers. Define a
be positive integers. Define a 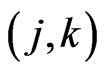 -grid to be a collection of segments
-grid to be a collection of segments
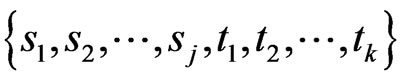 such that each segment si crosses each segment
such that each segment si crosses each segment  but such that segments
but such that segments 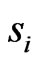 and
and  are disjoint if
are disjoint if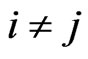 , as are
, as are 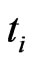 and
and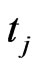 . If
. If 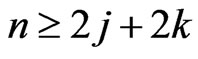 then the vertex set of a convex
then the vertex set of a convex 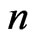 -gon clearly generates a
-gon clearly generates a 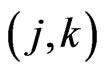 -grid. Define
-grid. Define 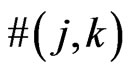 be the least integer such that any planar set of
be the least integer such that any planar set of  points in general position generates a
points in general position generates a 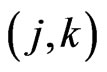 -grid. We again have the easy inequality
-grid. We again have the easy inequality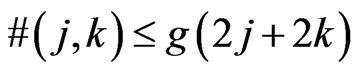 , but a result of Nielsen and Sabo [8] implies the linear upper bound
, but a result of Nielsen and Sabo [8] implies the linear upper bound
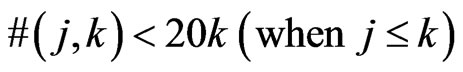 (0.3)
(0.3)
for these numbers.
It appears at least superficially, then, that grids are easier to find than are crossing families, and that both are easier to find than are convex polygons. But while the progression from 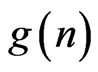 to
to 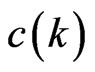 to
to  represents a geometric and computational simplification, none of these can be said to be simple. A look at the six-point cases illustrates the situation well.
represents a geometric and computational simplification, none of these can be said to be simple. A look at the six-point cases illustrates the situation well.
(A) The value of 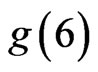 is not known. It is conjectured that
is not known. It is conjectured that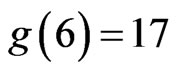 , but (0.1) gives only
, but (0.1) gives only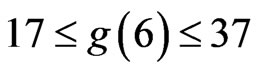 .
.
(B) The value of 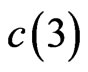 is not known, but we will prove in this paper that
is not known, but we will prove in this paper that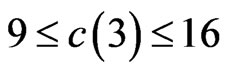 .
.
(C) We will show below that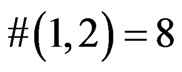 . However, this is the largest case for which the exact value of
. However, this is the largest case for which the exact value of  is known.
is known.
The purpose of this paper is to establish the facts mentioned in items (B) (see Section 1) and (C) (see Section 2). Bounds for some of the larger cases of these numbers will be given in a subsequent paper. The methods we use are not complicated, but some imagination is required to find an approach that reduces the number of cases to a manageable level.
2. An Improved Bound for c(3)
The bound (0.2) gives only —of course
—of course 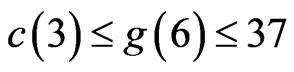 (from (0.1)) is better. We are able here to improve this substantially to
(from (0.1)) is better. We are able here to improve this substantially to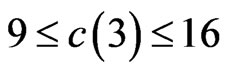 . We would be quite surprised if the actual value of
. We would be quite surprised if the actual value of 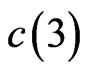 is not closer to the lower bound, but reducing the upper bound appears to be very difficult.
is not closer to the lower bound, but reducing the upper bound appears to be very difficult.
We begin by developing some notation that will be useful in the main proof. Let X be a finite planar set in general position. Now let A and B be vertices of the convex hull of X admitting parallel supporting lines. We may assume these supporting lines touch the convex hull of X only at points A and B so that the points of  lie in the strip between them. One of the half-strips bounded by these lines and the segment AB contains at least half the points of
lie in the strip between them. One of the half-strips bounded by these lines and the segment AB contains at least half the points of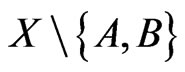 . Let this half-strip be called
. Let this half-strip be called , and let
, and let 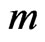 be the number of points of
be the number of points of 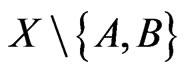 in
in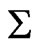 . We define sequences of sets
. We define sequences of sets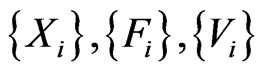 , and
, and 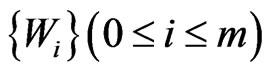 as follows (see Figure 1).
as follows (see Figure 1).
• Let .
.
• For each 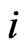 such that
such that 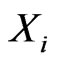 is defined let
is defined let  be the set consisting of those points in
be the set consisting of those points in  lying on the boundary of the convex hull of
lying on the boundary of the convex hull of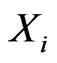 , together with the points
, together with the points 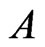 and
and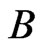 . Furthermore, set
. Furthermore, set  and
and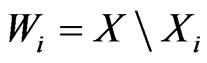 .
.
• Finally, for  let
let 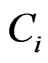 be a point of
be a point of 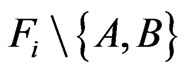 and define
and define 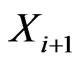 to be
to be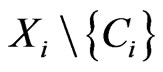 .
.
Note then that 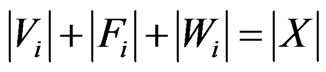 and that
and that
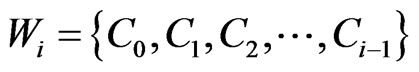 , so
, so . We think of
. We think of 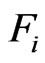 as being a “convex fence” separating
as being a “convex fence” separating 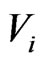 and
and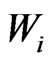 .
.
More generally, we will say that a sequence of points 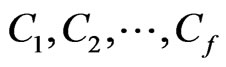 from
from 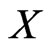 is a
is a 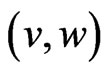 -fence for
-fence for 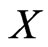 if
if
• 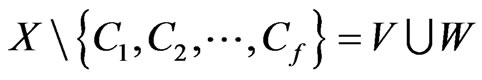 where
where  and
and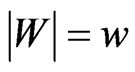 •
•  are consecutive vertices on the convex hull of
are consecutive vertices on the convex hull of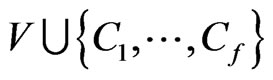 , and
, and
• every segment joining a point of V to a point of W crosses one of the f − 1 segments 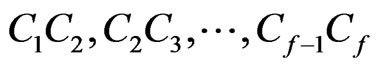 .
.
In this case we say that  is the set of points of
is the set of points of 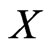 inside the fence
inside the fence  and
and 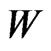 is the of points of
is the of points of 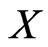 outside that fence.
outside that fence.
Given positive integers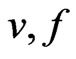 , and
, and  we will say that
we will say that 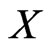 has property
has property  if
if 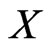 has a
has a 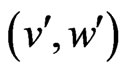 - fence consisting of
- fence consisting of 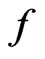 points for some
points for some 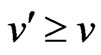 and
and . The sets described above yield a sequence of properties
. The sets described above yield a sequence of properties  , for X (where, of course,
, for X (where, of course,  and fm = 2).
and fm = 2).
Lemma 1.1. Let 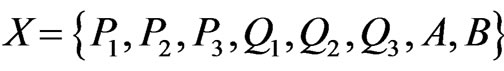 where
where

Figure 1. A convex fence.
for each i and j the segment 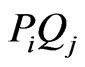 crosses AB. Then X generates a crossing family of three segments including
crosses AB. Then X generates a crossing family of three segments including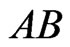 .
.
Clearly it is enough to show that 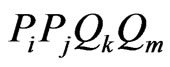 is a convex quadrilateral for some
is a convex quadrilateral for some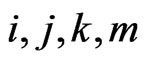 , and to do this it is enough to show that line
, and to do this it is enough to show that line 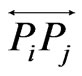 misses segment
misses segment  and line
and line 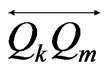 misses segment
misses segment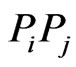 .
.
Note that the halfplane determined by 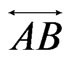 and containing
and containing 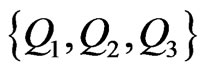 is divided into four (or fewer) regions by the lines
is divided into four (or fewer) regions by the lines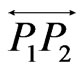 ,
,  , and
, and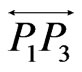 . Suppose first that one of these regions contains both
. Suppose first that one of these regions contains both 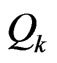 and
and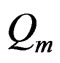 . Now
. Now 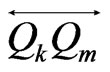 cannot intersect all three sides of the triangle
cannot intersect all three sides of the triangle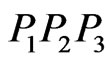 , so it misses some segment
, so it misses some segment . From our observation above the points generate a crossing family of six segments.
. From our observation above the points generate a crossing family of six segments.
If none of these regions contains two of the points of  then it must be the case that there is a segment
then it must be the case that there is a segment 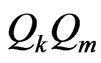 meeting exactly two of the lines
meeting exactly two of the lines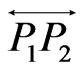 ,
,  ,
,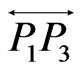 . But then
. But then 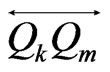 cannot meet any of the sides of the triangle
cannot meet any of the sides of the triangle 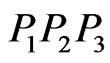 (since it cannot meet only one side of the triangle and there are two triangle sides that it clearly cannot meet, having crossed the lines determined by these sides at points outside of the triangle). But now
(since it cannot meet only one side of the triangle and there are two triangle sides that it clearly cannot meet, having crossed the lines determined by these sides at points outside of the triangle). But now 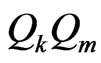 misses one of the lines
misses one of the lines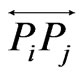 , so we once again have the situation described above.
, so we once again have the situation described above.
Lemma 1.2. If a set X has property 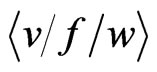 (with
(with 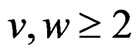 and
and ) and generates no crossing family of three segments then
) and generates no crossing family of three segments then 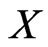 also has property
also has property  .
.
Proof. Let 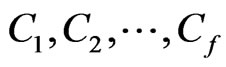 be a
be a 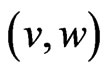 -fence for X with related components V and W. Order the points of
-fence for X with related components V and W. Order the points of 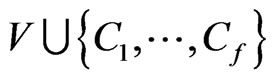 radially from
radially from 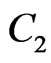 as
as
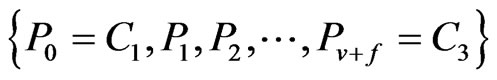 (see Figure 2).
(see Figure 2).
Now X generates no crossing family of three segments by assumption, so by Lemma 1.1 there cannot be three points of 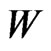 on the same side
on the same side 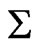 of line
of line  as point
as point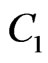 . (Again see Figure 2—the segment
. (Again see Figure 2—the segment 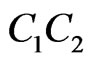 is crossed by every segment joining such a point of
is crossed by every segment joining such a point of  to any one of
to any one of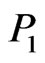 ,
, 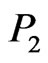 , or
, or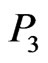 .) But then
.) But then 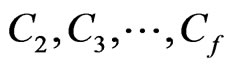 is a fence with related components
is a fence with related components  and
and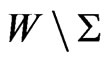 .
.
Lemma 1.3. Any set having property  for some
for some 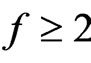 generates a crossing family of three segments.
generates a crossing family of three segments.
Proof. Assume to reach a contradiction that a set 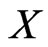
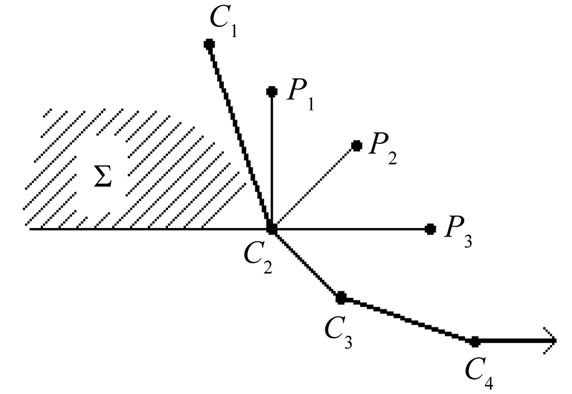
Figure 2. Illustrating the proof of Lemma 1.2.
has property 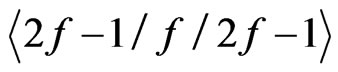 for some
for some 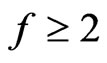 but generates no crossing family of three segments. Then by Lemma 1.2 X also has property
but generates no crossing family of three segments. Then by Lemma 1.2 X also has property . But by Lemma 1.1 any set with property
. But by Lemma 1.1 any set with property 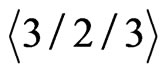 will generate a crossing family of three segments—a contradiction.
will generate a crossing family of three segments—a contradiction.
These lemmas establish that a set generates a crossing family of three segments if it contains a subset with a  -fence of two points or a
-fence of two points or a 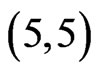 -fence of three points. This fact will be used repeatedly in our next proof.
-fence of three points. This fact will be used repeatedly in our next proof.
Theorem 1.4.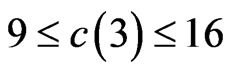 .
.
Proof. The lower bound is established by considering the set of eight points depicted in Figure 3. (A few lines are shown to indicate relative positioning of the points.) We leave it to the reader to verify that this set fails to generate any crossing family of three segments.
Now let X be any set of 16 points in general position. We will show that X generates a crossing family of three segments. The construction given at the outset of this section established a sequence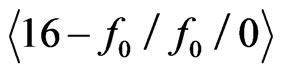 ,
,
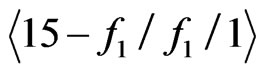 ,
, 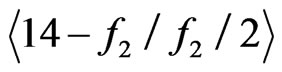 ,
,  ,
,
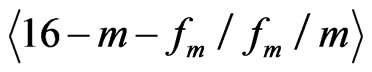 of properties for
of properties for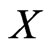 . Consider the property
. Consider the property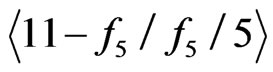 .
.
We may clearly assume 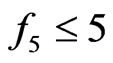 else
else  contains the vertices of a convex hexagon and thus clearly generates the desired crossing family. If
contains the vertices of a convex hexagon and thus clearly generates the desired crossing family. If  then we have either
then we have either  or
or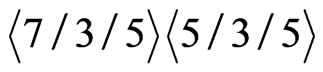 , either of which guarantees the crossing family by our preliminary lemmas. It remains, then, to examine the cases
, either of which guarantees the crossing family by our preliminary lemmas. It remains, then, to examine the cases 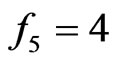 and
and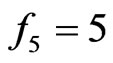 .
.
Case 1: 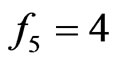
In this case, 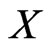 has property
has property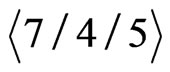 . As in Figure 4, let the fence be
. As in Figure 4, let the fence be 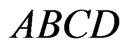 and consider the four regions
and consider the four regions ,
, 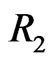 ,
, 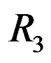 , and
, and 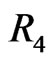 as shown. Let
as shown. Let  denote the number of points of
denote the number of points of 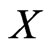 in region
in region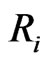 , so that
, so that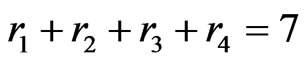 .
.
If r1 > 0 and r3 > 0 (or similarly if r2 > 0 and r4 > 0) it is easy to see that X then generates a crossing family of three segments (two of which are AC and BD). So, if r1 > 0 then we may assume either  or
or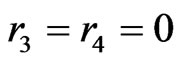 . This means either ACD or ABD is a
. This means either ACD or ABD is a 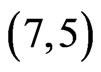 -fence, so our
-fence, so our
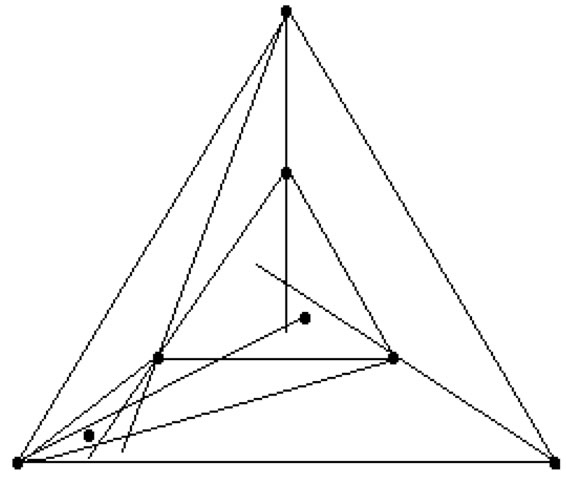
Figure 3. Example showing c(3) ≥ 9.
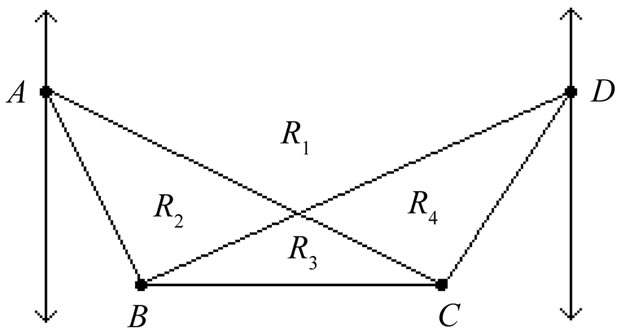
Figure 4. The general situation for Case 1.
preliminary lemmas would guarantee the desired crossing family for X. Thus, we may assume 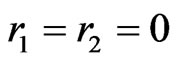 and
and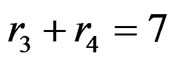 .
.
If 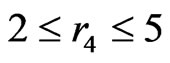 then (using the points in
then (using the points in  and
and 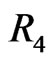 along with points B and D) AC is a
along with points B and D) AC is a 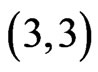 -fence. On the other hand, if
-fence. On the other hand, if 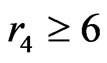 then ACD is a
then ACD is a 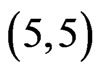 -fence. So (again using our lemmas) we may assume
-fence. So (again using our lemmas) we may assume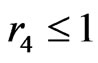 .
.
Subcase 1A: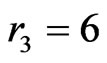 ,
, 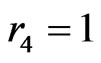
Order the points of 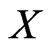 in regions
in regions 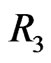 and
and 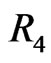 as
as 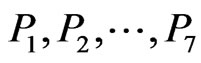 radially from
radially from 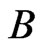 as in Figure 5. We may assume that the region
as in Figure 5. We may assume that the region  in that figure (bounded by
in that figure (bounded by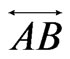 ,
, 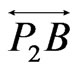 , and the supporting line through
, and the supporting line through 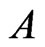 to the convex hull of
to the convex hull of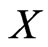 ) contains at most two points of
) contains at most two points of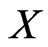 , else
, else 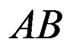 is a
is a 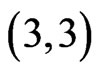 -fence (with the latter set of three points being
-fence (with the latter set of three points being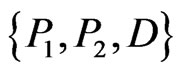 ). But then
). But then  is a
is a 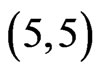 - fence where the points inside consist of the points in region
- fence where the points inside consist of the points in region 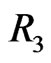 less
less 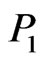 (if
(if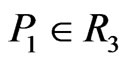 ) and the points outside consist of the (at least three) points outside ABCD not lying in
) and the points outside consist of the (at least three) points outside ABCD not lying in  together with D and the point of X in region
together with D and the point of X in region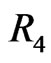 . By our preliminary lemmas, X then generates a crossing family of three segments.
. By our preliminary lemmas, X then generates a crossing family of three segments.
Subcase 1B: ,
, 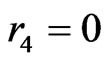
Consider now the region 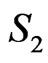 in Figure 6 (bounded by
in Figure 6 (bounded by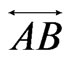 ,
, 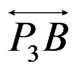 , and the supporting line). If this region contains two points of X then BD is a
, and the supporting line). If this region contains two points of X then BD is a  -fence where one set of three points is
-fence where one set of three points is  and the other consists of the two points in
and the other consists of the two points in 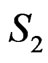 together with point A. Thus, we may assume
together with point A. Thus, we may assume 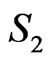 contains no more than one point of X.
contains no more than one point of X.
This shows that by discarding up to two points (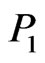 and
and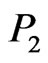 ) inside and one point (in
) inside and one point (in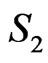 ) outside the fence
) outside the fence 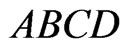 we can eliminate all segments (joining an inside point to an outside point) that cross AB. A mirror image of this same argument can be done for eliminating segments that cross CD. In this way we conclude that we can discard four points inside ABCD and two points outside ABCD and eliminate all segments except those that cross BC. So, BC is a
we can eliminate all segments (joining an inside point to an outside point) that cross AB. A mirror image of this same argument can be done for eliminating segments that cross CD. In this way we conclude that we can discard four points inside ABCD and two points outside ABCD and eliminate all segments except those that cross BC. So, BC is a  -fence for the remaining subset of X. As before, this is sufficient to guarantee that X generates the desired crossing family.
-fence for the remaining subset of X. As before, this is sufficient to guarantee that X generates the desired crossing family.
Case 2: 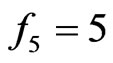
In this case, X has property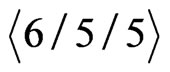 . Consider the convex hull of the five points making up the fence
. Consider the convex hull of the five points making up the fence . The diagonals of this pentagon determine eleven interior regions. If a point of X lies in any of the
. The diagonals of this pentagon determine eleven interior regions. If a point of X lies in any of the
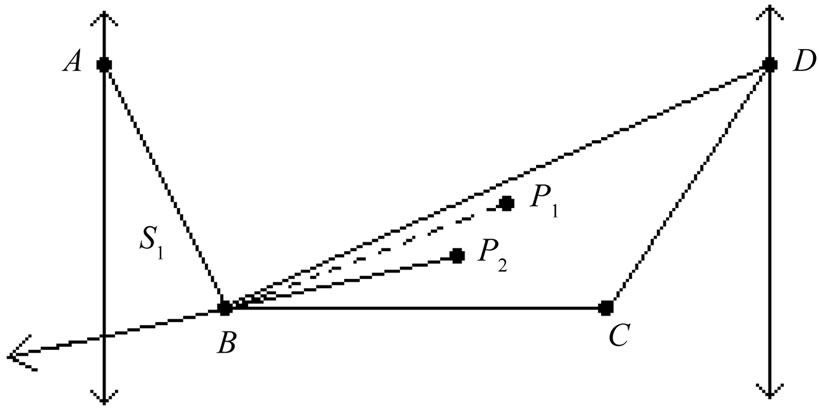
Figure 5. The arrangement for Subcase 1A.
Figure 6. The arrangement for Subcase 1B.
five regions bounded by segments of the pentagon or in the central region bounded by all the diagonals, then 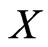 generates a crossing family of three segments as shown in Figure 7.
generates a crossing family of three segments as shown in Figure 7.
Thus, we may assume that the six points of 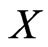 inside the fence
inside the fence 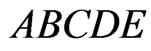 lie in the five regions labeled
lie in the five regions labeled 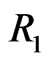 through
through 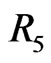 in Figure 8. As before, let
in Figure 8. As before, let 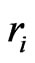 denote the number of points of
denote the number of points of 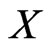 in region
in region .
.
• If points of X lie in each of two adjacent regions from among R1 through R5 then it is easy to construct a crossing family of three segments (two are diagonals of ABCDE and the other joins the points in question).
• If 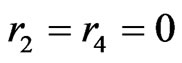 then ACE is a
then ACE is a 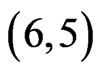 -fence—more than enough to guarantee the desired crossing family.
-fence—more than enough to guarantee the desired crossing family.
Putting together these two observations, we may now assume that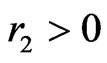 ,
, 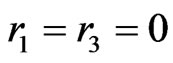 , either
, either 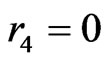 or
or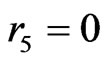 , and (of course)
, and (of course)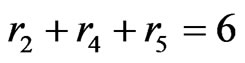 .
.
• If 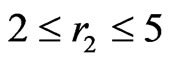 then AC is a
then AC is a 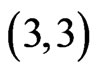 -fence where on one side we include two of the points from region
-fence where on one side we include two of the points from region  along with B and on the other side we include a point from
along with B and on the other side we include a point from  along with D and E.
along with D and E.
• If 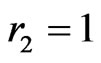 then either R4 or R5 contains 5 points of X. If R4 contains these points then CE is a
then either R4 or R5 contains 5 points of X. If R4 contains these points then CE is a 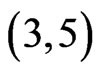 -fence where the three points on one side consist of the point in R2 together with A and B. If the points lie in R5 then similarly AD is a
-fence where the three points on one side consist of the point in R2 together with A and B. If the points lie in R5 then similarly AD is a 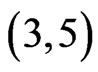 -fence.
-fence.
Both of the above cases, then, lead to a crossing family of three segments generated by X. The only remaining case to consider is 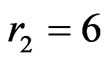 (and
(and ). Here, ABDE is a
). Here, ABDE is a 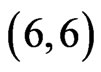 -fence for X (where we include C with the points outside the fence). Note that Lemma 1.2 would allow us to conclude that either X generates a crossing family of three segments or else its property
-fence for X (where we include C with the points outside the fence). Note that Lemma 1.2 would allow us to conclude that either X generates a crossing family of three segments or else its property
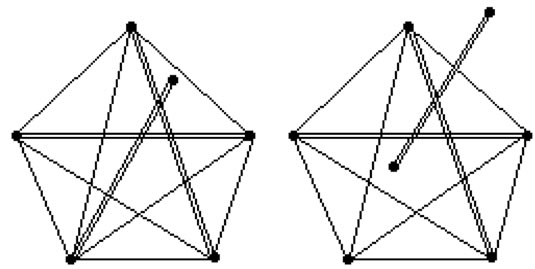
Figure 7. Crossing families in easy instances of Case 2.
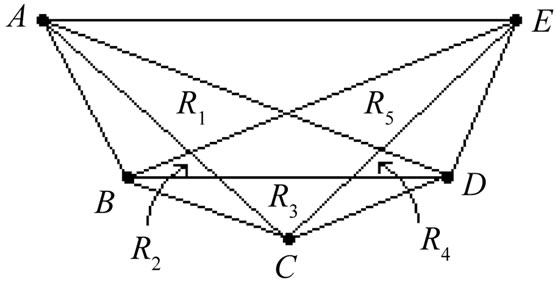
Figure 8. The arrangement for the remaining parts of Case 2.
 must imply property
must imply property 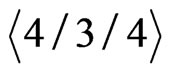 (and
(and
 ). Unfortunately, that is not sufficient under our lemmas to give the desired conclusion. Instead, we will need to be more careful in reducing the fence.
). Unfortunately, that is not sufficient under our lemmas to give the desired conclusion. Instead, we will need to be more careful in reducing the fence.
For our first step in the reduction, order the points of X in region  as
as  through
through 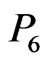 radially from B as in Figure 9. We may assume the region
radially from B as in Figure 9. We may assume the region 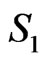 in that figure contains no more than one point of X, since otherwise BE is a
in that figure contains no more than one point of X, since otherwise BE is a  -fence (with two points from
-fence (with two points from 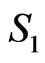 and A on one side and
and A on one side and 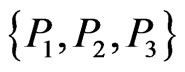 on the other). Then discarding any point in
on the other). Then discarding any point in 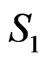 along with
along with 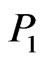 and
and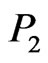 , we may eliminate all segments (joining a point inside
, we may eliminate all segments (joining a point inside  to a point outside) that cross
to a point outside) that cross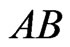 ; all this while leaving at least four inside points and at least five outside points.
; all this while leaving at least four inside points and at least five outside points.
The second part of the reduction is accomplished by ordering the remaining points of X in R2 as Q1 through Q4 radially from D as in Figure 10. We may assume the region labeled as S2 in that figure contains no more than 2 points of X, else 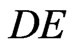 is a
is a 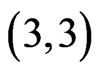 -fence (with three points from S2 on one side and
-fence (with three points from S2 on one side and 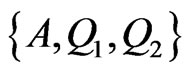 on the other). Thus, discarding points in
on the other). Thus, discarding points in 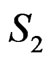 along with Q1, BD is now a
along with Q1, BD is now a  -fence for the remaining set, and our reduction is complete.
-fence for the remaining set, and our reduction is complete.
We have demonstrated that in every possible case the set X must generate a crossing family of three segments, so the theorem is proved.
3. An Exact Value for #(1,2)
Here we prove the only exact value known for any of the six-point configuration numbers mentioned in the introduction. The following well-known fact will prove useful in the analysis.
Lemma 2.1: Suppose that
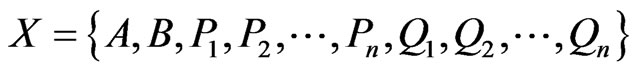 where for each
where for each 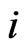 and j the segment
and j the segment 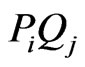 crosses AB. Then X generates a
crosses AB. Then X generates a 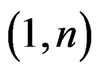 -grid consisting of n pairwise disjoint segments
-grid consisting of n pairwise disjoint segments
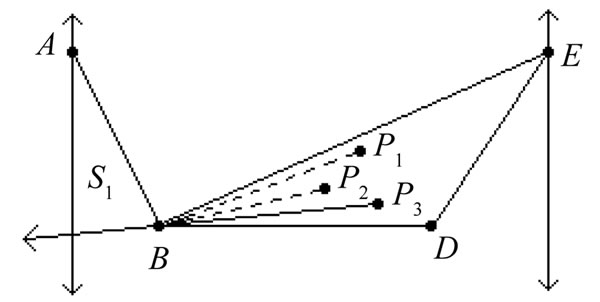
Figure 9. The first step in reducing the fence for Case 2.
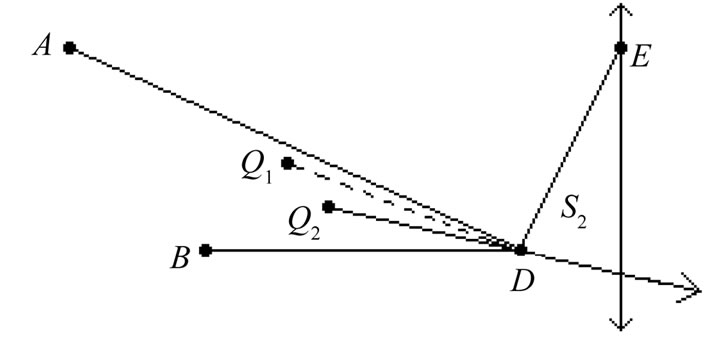
Figure 10. The second step in reducing the fence for Case 2.
each of which crosses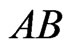 .
.
Proof. Let π be the permutation of  such that the sum of the lengths of the segments
such that the sum of the lengths of the segments 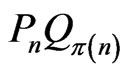 is minimized. Then the segments
is minimized. Then the segments
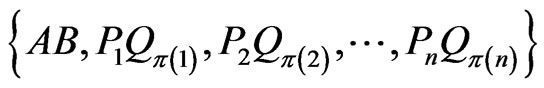 form a
form a  -grid.
-grid.
Theorem 2.2: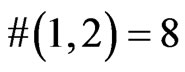 .
.
Proof. Figure 11 shows a set of seven points that generates no  -grids. (This is easily checked by hand.)
-grids. (This is easily checked by hand.)
It remains to prove that any set of eight points in general position will generate a 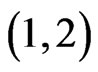 -grid. Let
-grid. Let 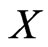 be any such set, let
be any such set, let 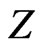 be a vertex of the convex hull of
be a vertex of the convex hull of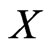 , and let
, and let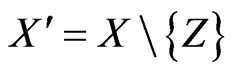 . We consider several cases depending on the shape of the convex hull of
. We consider several cases depending on the shape of the convex hull of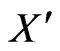 .
.
Case 1. If the convex hull of 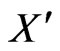 is a 6-gon or 7-gon then
is a 6-gon or 7-gon then 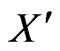 clearly generates a
clearly generates a 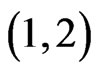 -grid.
-grid.
Case 2. Suppose the convex hull of 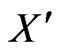 is a 5-gon
is a 5-gon  with the remaining points of
with the remaining points of 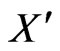 being P and Q. If P and Q lie on opposite sides of any diagonal to ABCDE then
being P and Q. If P and Q lie on opposite sides of any diagonal to ABCDE then 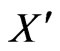 generates a (1,2)-grid by Lemma 2.1. Consequently, we may assume that P and Q lie in the “inner pentagon” determined by the diagonals. We may also assume that Q is interior to the triangle PAB. But then QD crosses both the diagonal CE and either PA or PB, giving us a (1,2)-grid (see Figure 12).
generates a (1,2)-grid by Lemma 2.1. Consequently, we may assume that P and Q lie in the “inner pentagon” determined by the diagonals. We may also assume that Q is interior to the triangle PAB. But then QD crosses both the diagonal CE and either PA or PB, giving us a (1,2)-grid (see Figure 12).
Case 3. If the convex hull of 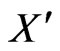 is a quadrilateral ABCD then the three points
is a quadrilateral ABCD then the three points 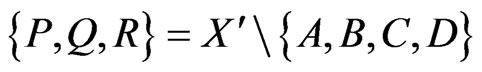 must be distributed between the four regions determined by the diagonals of
must be distributed between the four regions determined by the diagonals of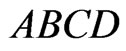 . By Lemma 2.1 we may assume that these points are not separated by either diagonal—thus all lie in the same region.
. By Lemma 2.1 we may assume that these points are not separated by either diagonal—thus all lie in the same region.
Assume then that P, Q, and R are each interior to both triangles ABC and BCD. If points 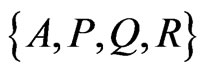 form the vertices of a convex quadrilateral then its diagonals together with segment BD form a
form the vertices of a convex quadrilateral then its diagonals together with segment BD form a  -grid (see the left
-grid (see the left
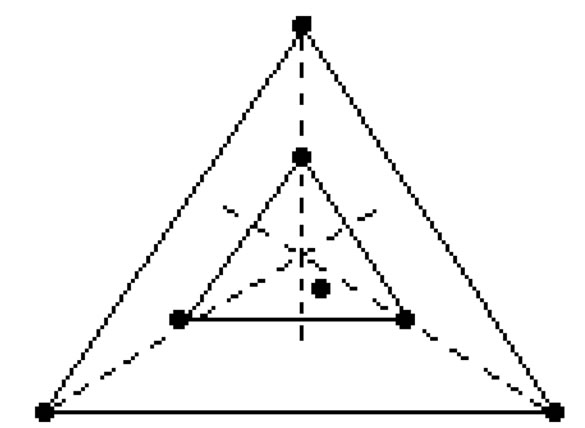
Figure 11. A set of seven points with no (1,2)-grid.
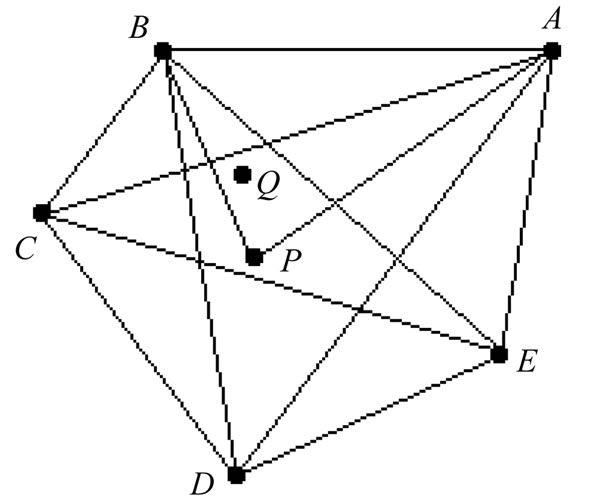
Figure 12. A (1,2)-grid for Case 2.
half of Figure 13). Thus, we may also assume that R is interior to the triangle APQ as in the right half of Figure 13. We now consider some subcases. Recall that there is a point Z of set X lying outside of the convex hull of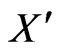 . The segment RZ must meet either BC or one or both of the diagonals of ABCD.
. The segment RZ must meet either BC or one or both of the diagonals of ABCD.
Subcase 3A. Suppose first that RZ meets BC. Note that it must also meet one of the sides of triangle APQ, and that this side is disjoint from BC. Thus X generates a (1,2)-grid in this case.
Subcase 3B. Next suppose that RZ meets exactly one of the diagonals of ABCD. Then these diagonals together with RZ form a (1,2)-grid.
Subcase 3C. Finally, suppose that RZ meets both diagonals of ABCD. In particular, then, RZ meets BD. But BD meets both AP and AQ, and RZ must miss one of these. So, this case also yields a generated (1,2)-grid.
Case 4. The only remaining case is to assume that the convex hull of 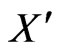 is a triangle, say ABC, with the four remaining points of
is a triangle, say ABC, with the four remaining points of 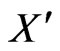 interior to this triangle. If ZABC is a convex quadrilateral then by separating B from the remaining seven points we reduce to one of the earlier cases (see Figure 14).
interior to this triangle. If ZABC is a convex quadrilateral then by separating B from the remaining seven points we reduce to one of the earlier cases (see Figure 14).
Thus we may assume that C is interior to triangle ZAB (so that the convex hull of X is a triangle). We may clearly assume that a similar configuration results if any of the three vertices of this triangle are separated from the other seven points. In this case the set X must be as pictured in Figure 15: the convex hull of X is a triangle  and the convex hull of
and the convex hull of 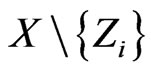 is a triangle with
is a triangle with 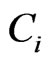 as the third vertex. Two points of X, say P and Q, must lie in the region common to the interiors of triangles
as the third vertex. Two points of X, say P and Q, must lie in the region common to the interiors of triangles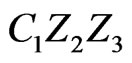 ,
, 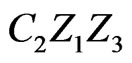 , and
, and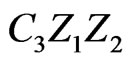 . We consider two subcases for the placement of these points.
. We consider two subcases for the placement of these points.
Subcase 4A. First it is possible that either P or Q is not interior to triangle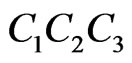 . Assume, for instance, that segment
. Assume, for instance, that segment 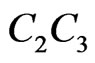 separates P from
separates P from 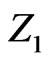 as in Figure 16. In this case
as in Figure 16. In this case  meets both
meets both  and one of
and one of 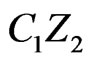 or
or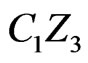 , yielding a (1,2)-grid.
, yielding a (1,2)-grid.
Subcase 4B. Finally, assume both P and Q lie interior to triangle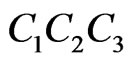 . The ray PQ must meet one of the sides of this triangle, say
. The ray PQ must meet one of the sides of this triangle, say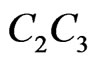 . Then Q is interior to triangle
. Then Q is interior to triangle 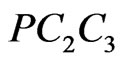 so we have the configuration depicted in Figure 17. The segment
so we have the configuration depicted in Figure 17. The segment 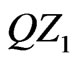 must now meet a side
must now meet a side
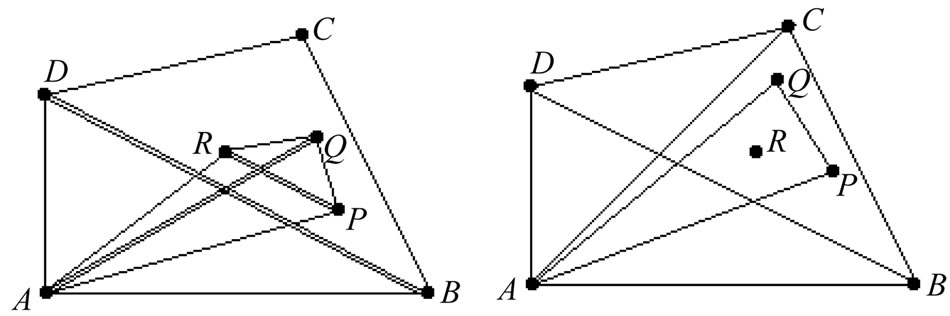
Figure 13. Possibilites for Case 3.

Figure 14. Reducing an instance of Case 4 to a previous case.
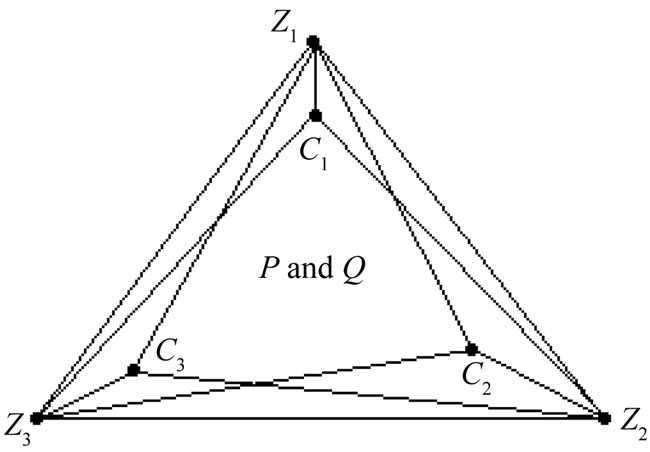
Figure 15. The difficult part of Case 4.
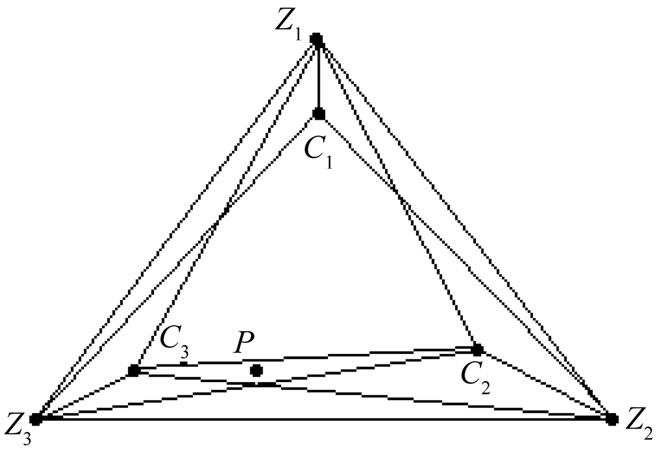
Figure 16. The arrangement for Subcase 4A.
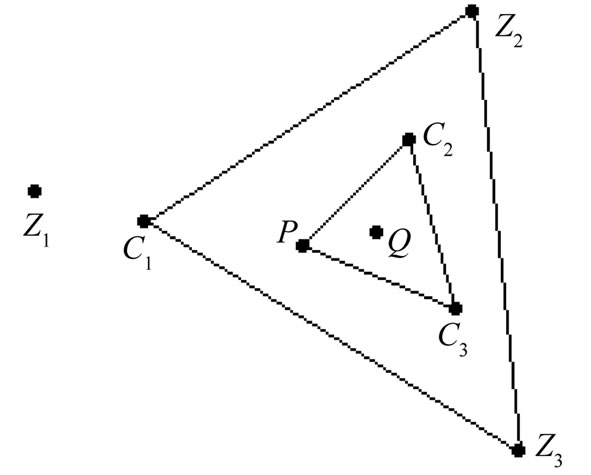
Figure 17. The arrangement for Subcase 4B.
of each of the triangles  and
and , again yielding a (1,2)-grid.
, again yielding a (1,2)-grid.
All cases have now been considered and the proof is complete.
REFERENCES
- P. Erdös and G. Szekeres, “A Combinatorial Problem in Geometry,” Compositio Mathematica, Vol. 2, 1935, pp. 463-470. (Reprinted in: J. Spenceer, Ed., Paul Erdös: Selected Writings, MIT Press, Cambridge, 1973, pp. 3-12. Also Reprinted in: I. Gessel and G.-C. Rota, Eds., Classic Papers in Combinatorics, Birkhäuser, Basel, 1987, pp. 49-56.)
- P. Erdös and G. Szekeres, “On Some Extremum Problems in Elementary Geometry,” Annales Universitatis Scientarium Budapestinensis de Rolando Eötvös Nominatae Sectio Mathematica, Vol. 3-4, No. 1, 1961, pp. 53-62. (Reprinted in: J. Spencer, Ed., Paul Erdös: The Art of Counting. Selected Writings, MIT Press, Cambridge, 1973, pp. 680-689.)
- F. R. L. Chung and R. L. Graham, “Forced Convex nGons in the Plane,” Discrete & Computational Geometry, Vol. 19, No. 3, 1998, pp. 367-371. doi:10.1007/PL00009353
- D. Kleitman and L. Pachter, “Finding Convex Sets among Points in the Plane,” Discrete & Computational Geometry, Vol. 19, No. 3, 1998, pp. 405-410. doi:10.1007/PL00009358
- G. Tóth and P. Valtr, “Note on the Erdös-Szekeres Theorem,” Discrete & Computational Geometry, Vol. 19, No. 3, 1998, pp. 457-459. doi:10.1007/PL00009363
- W. Morris and V. Soltan, “The Erdös-Szekeres Problem on Points in Convex Position—A Survey,” Bulletin of the American Mathematical Society, Vol. 37, No. 4, 2000, pp. 437-458.
- B. Aronov, P. Erdös, W. Goddard, D. J. Kleitman, M. Klugerman, J. Pach and L. J. Schulman, “Crossing Families,” Combinatorica, Vol. 14, No. 2, 1994, pp. 127-134. doi:10.1007/BF01215345
- M. J. Nielsen and D. E. Sabo, “Transverse Families of Matchings in the Plane,” ARS Combinatoria, Vol. 55, No. 55, 2000, pp. 193-199.

