Open Journal of Discrete Mathematics
Vol.3 No.1(2013), Article ID:27391,3 pages DOI:10.4236/ojdm.2013.31011
Reverse Total Signed Vertex Domination in Graphs
Department of Mathematics and Information Sciences, Langfang Teachers College, Langfang, China
Email: wsli@live.cn
Received November 20, 2012; revised December 20, 2012; accepted December 27, 2012
Keywords: Reverse Total Signed Vertex Domination; Upper Bounds; Complete Bipartite Graph
ABSTRACT
Let 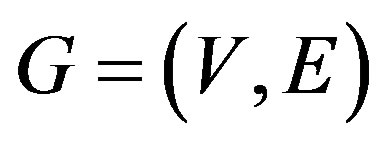 be a simple graph with vertex set V and edge set E. A function
be a simple graph with vertex set V and edge set E. A function 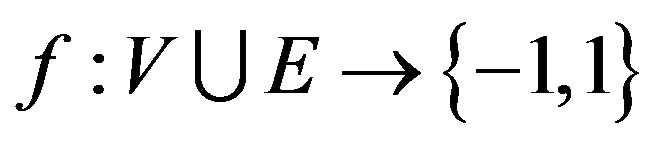 is said to be a reverse total signed vertex dominating function if for every
is said to be a reverse total signed vertex dominating function if for every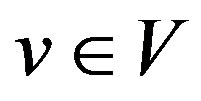 , the sum of function values over
, the sum of function values over 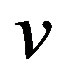 and the elements incident to
and the elements incident to  is less than zero. In this paper, we present some upper bounds of reverse total signed vertex domination number of a graph and the exact values of reverse total signed vertex domination number of circles, paths and stars are given.
is less than zero. In this paper, we present some upper bounds of reverse total signed vertex domination number of a graph and the exact values of reverse total signed vertex domination number of circles, paths and stars are given.
1. Introduction
In this paper we shall use the terminology of [1]. Let 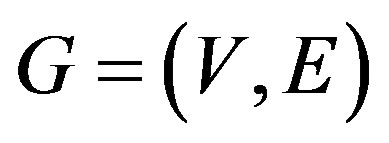 be a simple graph with vertex set
be a simple graph with vertex set 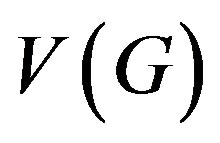 and edge set
and edge set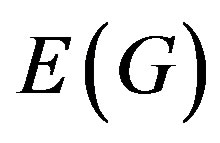 . Let
. Let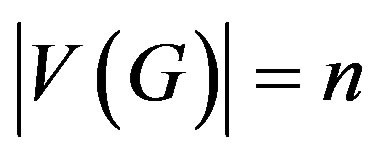 ,
,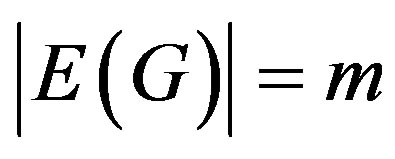 . For every
. For every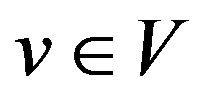 , the open neighborhood of
, the open neighborhood of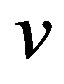 , denoted by
, denoted by , is a set
, is a set 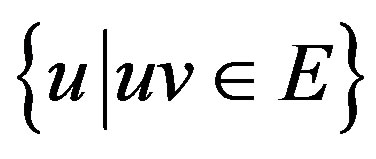 and the closed neighborhood of
and the closed neighborhood of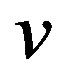 , denoted by
, denoted by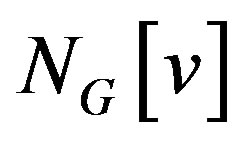 , is a set
, is a set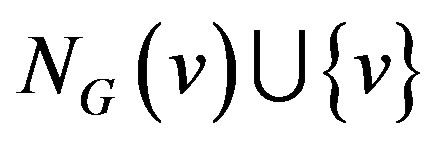 . We write
. We write 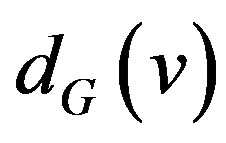 for the degree of a vertex
for the degree of a vertex 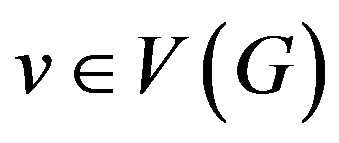 and the maximum and minimum degree of
and the maximum and minimum degree of 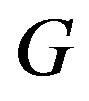 are denoted by
are denoted by  and
and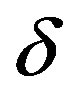 , respectively. For every
, respectively. For every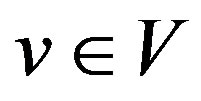 , the edge-closed neighborhood of
, the edge-closed neighborhood of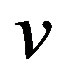 , denoted by
, denoted by , is
, is
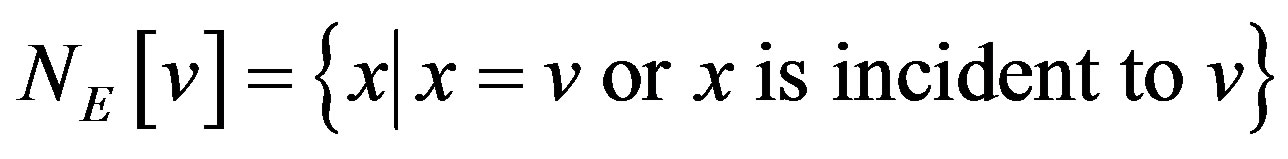 .
.
Many domination parameters in graphs has been studied richly [2-4] A function 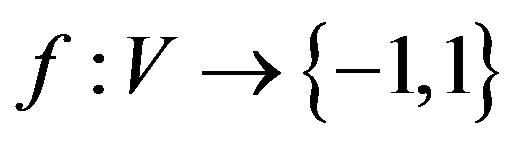 is a signed dominating function if for every vertex
is a signed dominating function if for every vertex
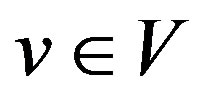 ,
,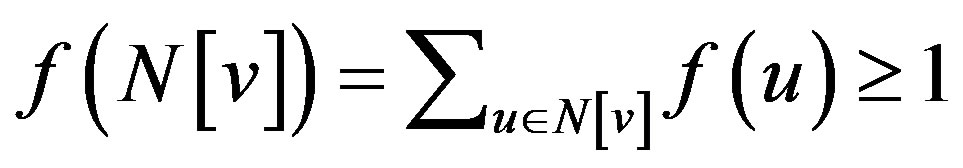 .
.
The weight 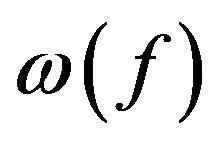 of
of 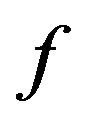 is the sum of the function values of all vertices in
is the sum of the function values of all vertices in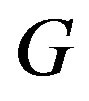 . The signed domination number
. The signed domination number 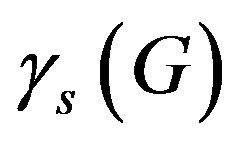 of
of 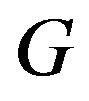 is the minimum weight of signed dominating functions on
is the minimum weight of signed dominating functions on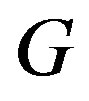 . This concept was introduced by Dunbar et al. [5] and has been studied by several authors [6-9]. As an extension of the signed domination, we give the definition of the reverse total signed vertex domination in a graph.
. This concept was introduced by Dunbar et al. [5] and has been studied by several authors [6-9]. As an extension of the signed domination, we give the definition of the reverse total signed vertex domination in a graph.
Definition 1. Let 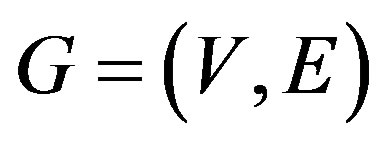 be a simple graph. A reverse total signed vertex dominating function of
be a simple graph. A reverse total signed vertex dominating function of 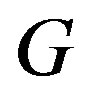 is a function
is a function 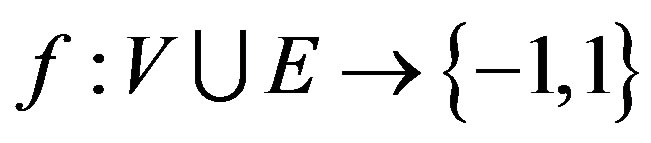 such that
such that 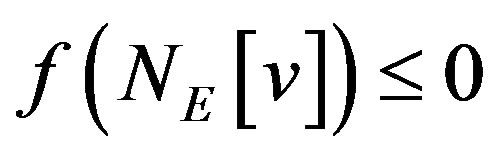
for all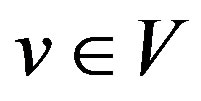 . The reverse total signed vertex domination number of
. The reverse total signed vertex domination number of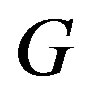 , denoted by
, denoted by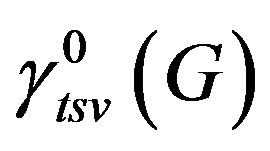 , is the maximum weight of a reverse total signed vertex dominating function of
, is the maximum weight of a reverse total signed vertex dominating function of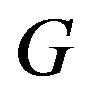 . A reverse total signed vertex dominating function
. A reverse total signed vertex dominating function 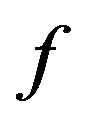 is called a
is called a  -function of
-function of 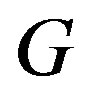 if
if 
 .
.
2. Properties of Reverse Total Signed Vertex Domination
Proposition 1 For any graph ,
,
 .
.
Proof. Let  be a
be a  -function of
-function of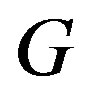 . Then
. Then
 .
.
Let
 ,
,
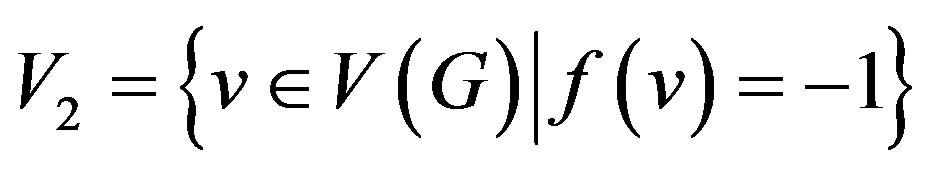 ,
,
 ,
,
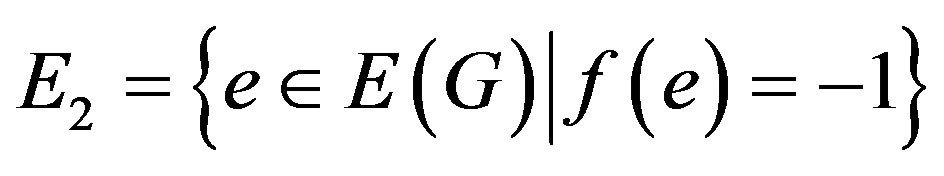 .
.
Then
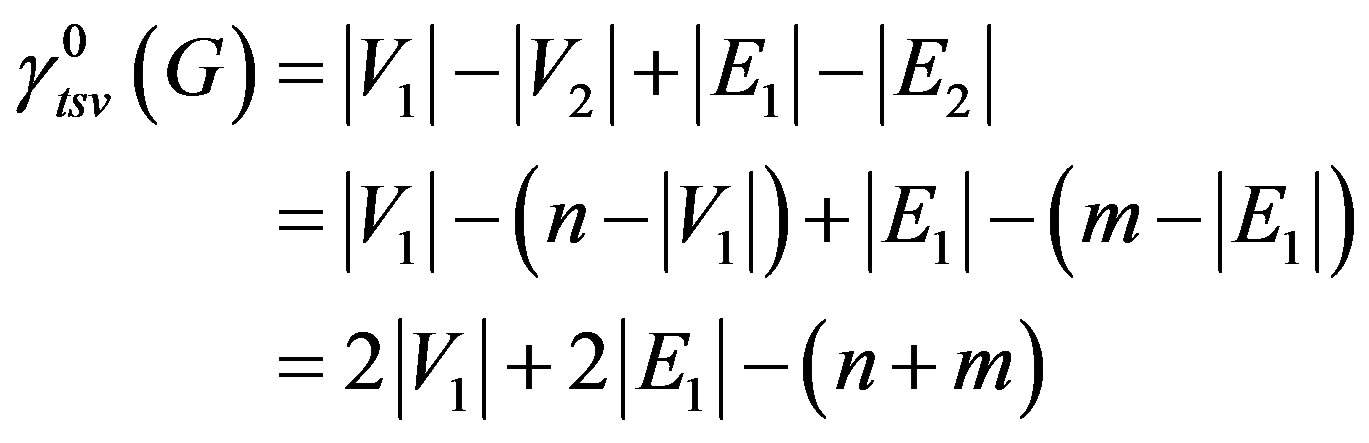 .
.
Therefore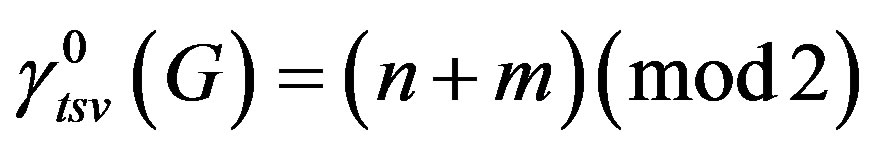 .
.
Propositon 2 For any graph ,
, .
.
Proof. Let 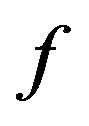 be a
be a  -function of
-function of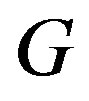 . Then for every
. Then for every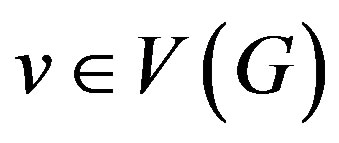 ,
, 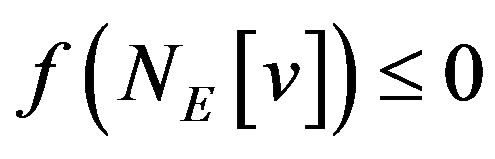 and we have
and we have
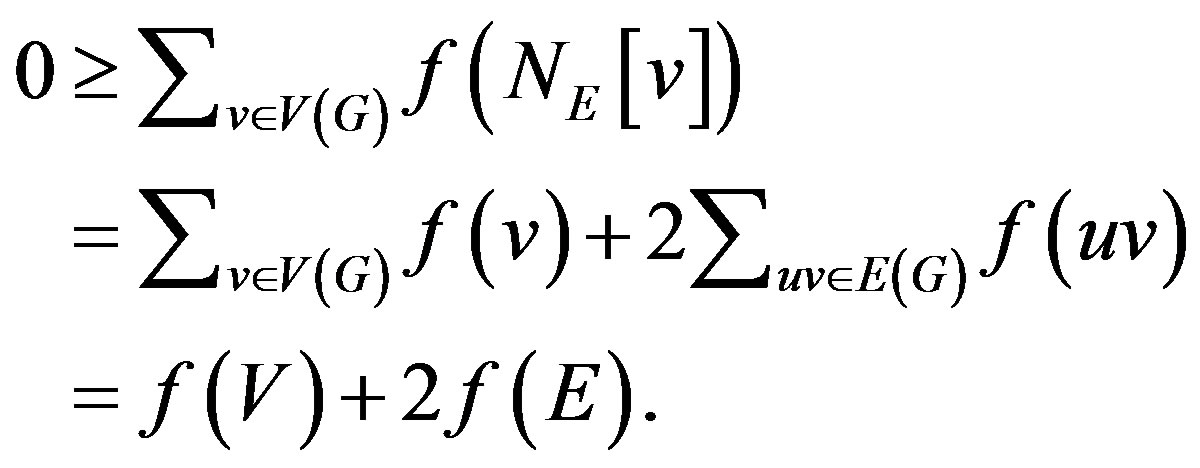
Thus .
.
Propositon 3 For any graph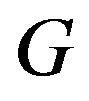 ,
,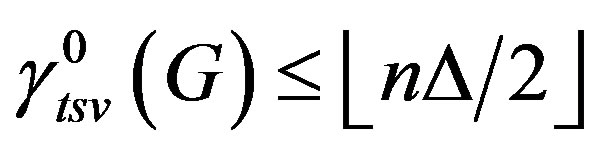 .
.
Proof. Let 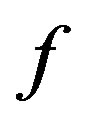 be a
be a 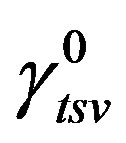 -function of
-function of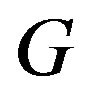 .
.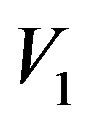 ,
,  ,
, 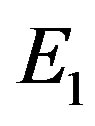 and
and  are defined as Proposition 2. Then
are defined as Proposition 2. Then
 .
.
We define two induced graphs  and
and 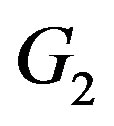 of
of 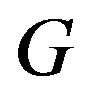 as follows:
as follows:
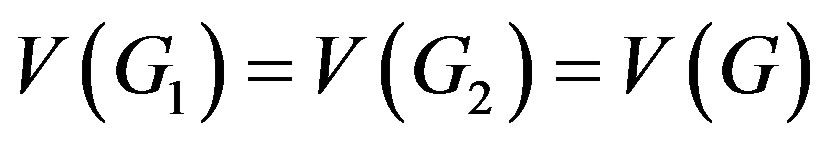 ,
, 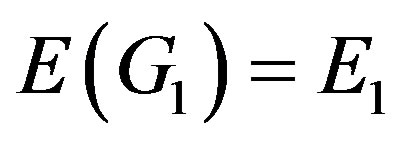 ,
, .
.
Then for every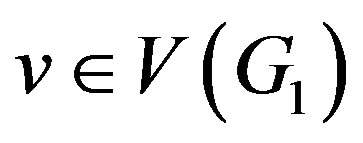 ,
,
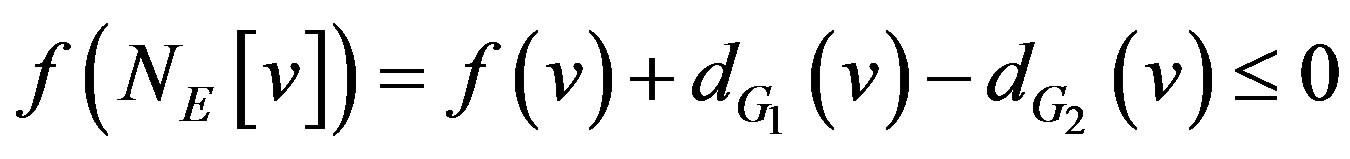
and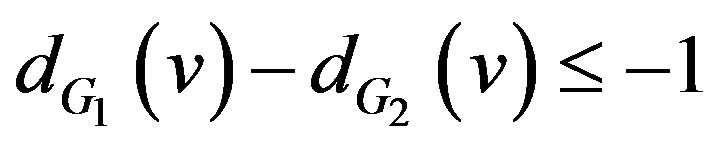 . For every
. For every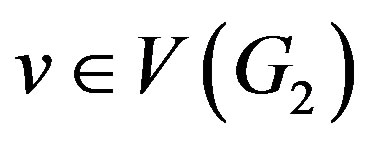 , we have
, we have
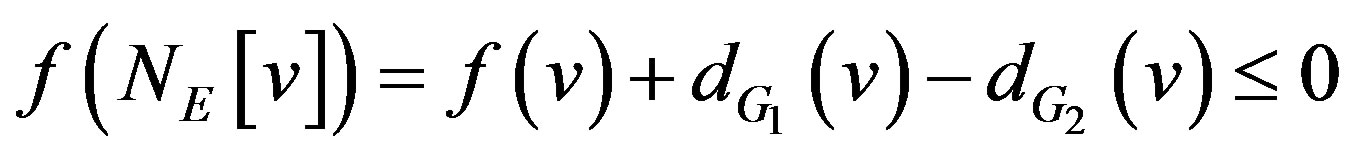
and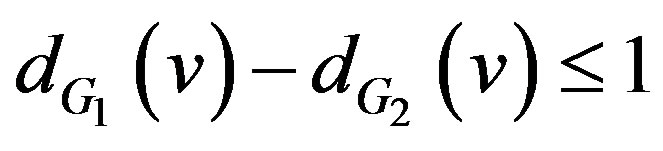 . Thus
. Thus
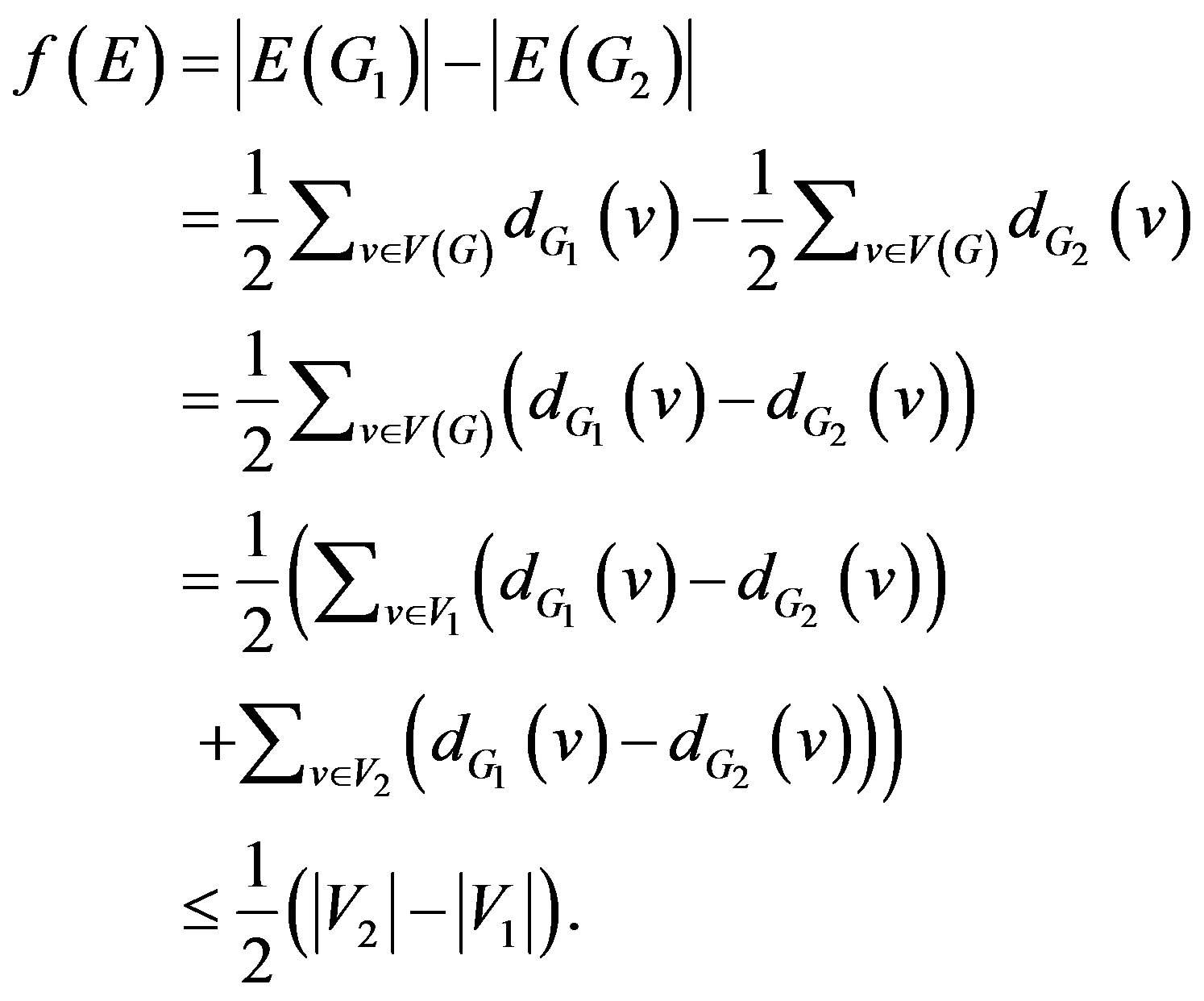
Therefore
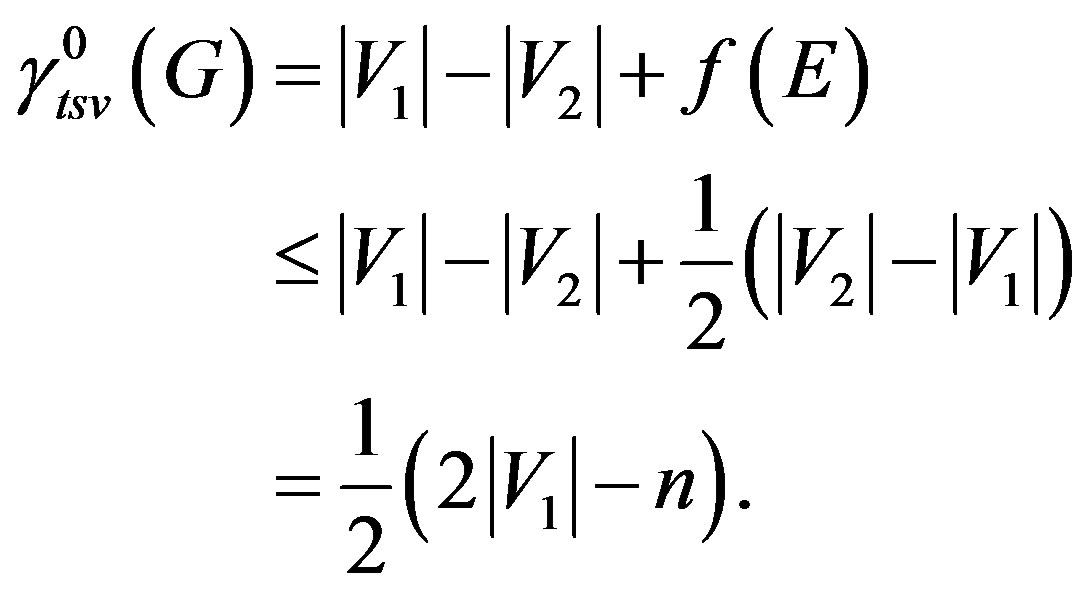
Since
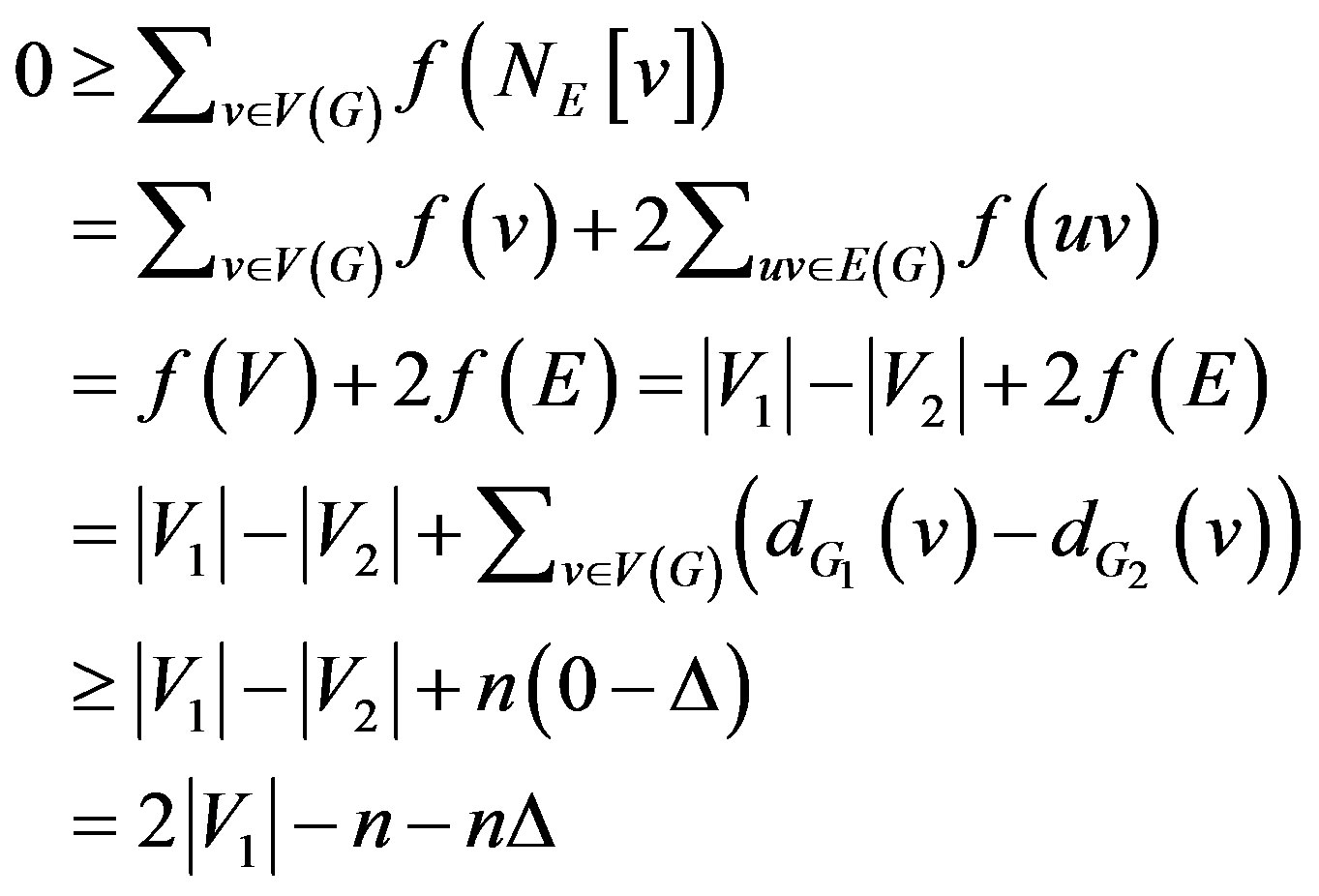 we have
we have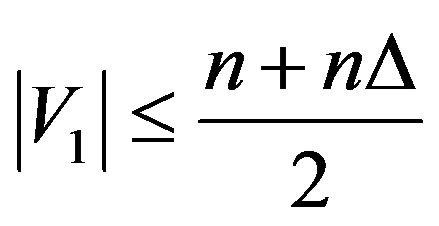 . Therefore
. Therefore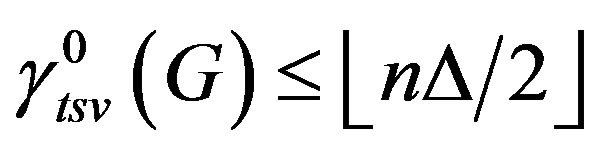 .
.
Propositon 4 For any star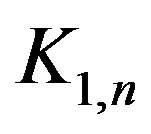 ,
, .
.
Proof. Let  be a
be a 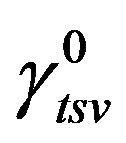 -function. Let
-function. Let
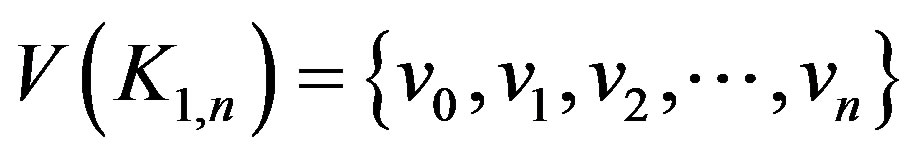 ,
,
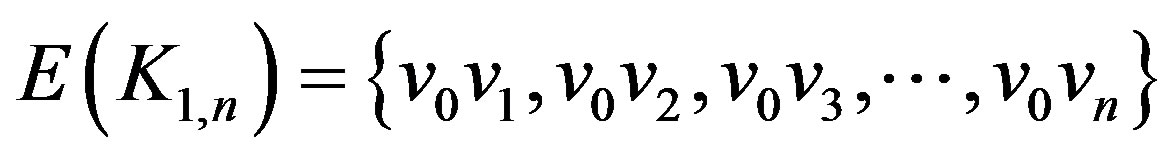 ,
,
where 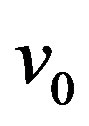 is the center of
is the center of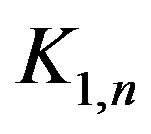 . Since for every
. Since for every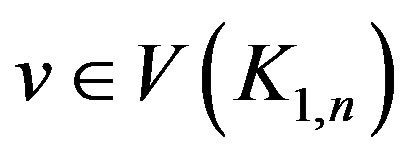 ,
, 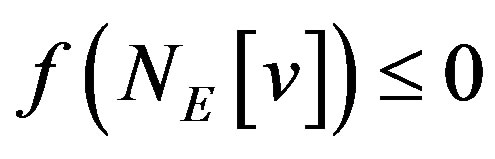 , we have
, we have
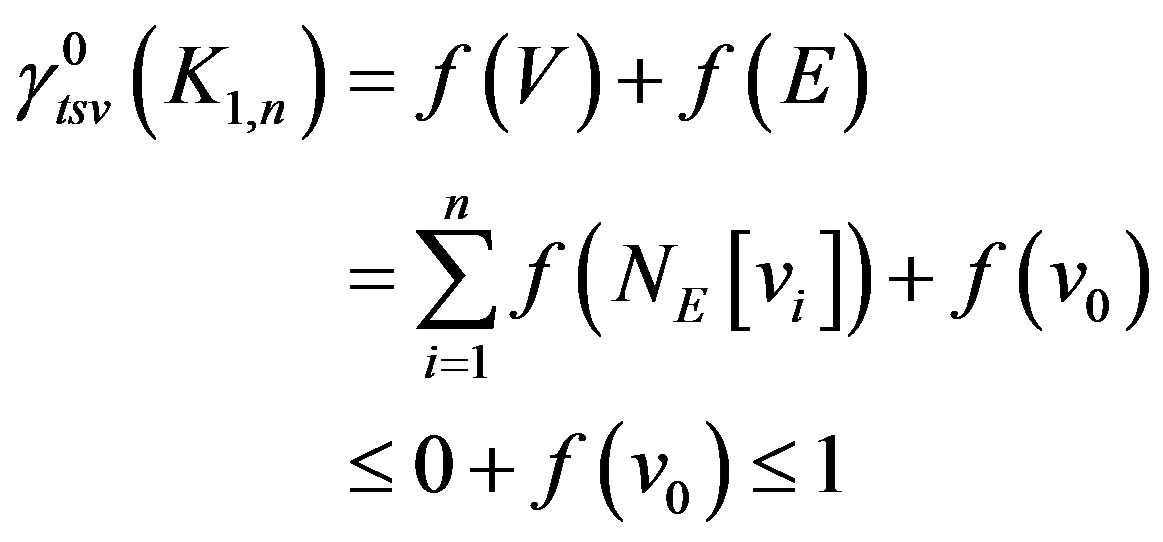 .
.
On the other hand, consider the function
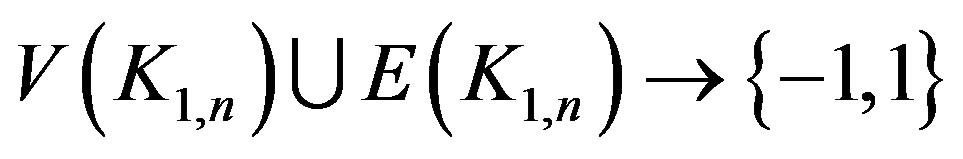
 such that
such that
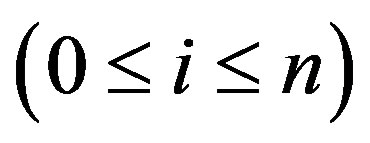
 ,
,
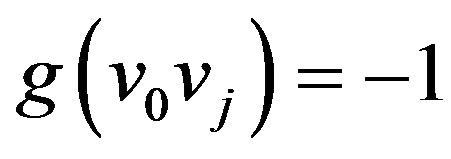 .
.
Then 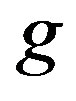 is a reverse total signed vertex dominating function on
is a reverse total signed vertex dominating function on  and
and
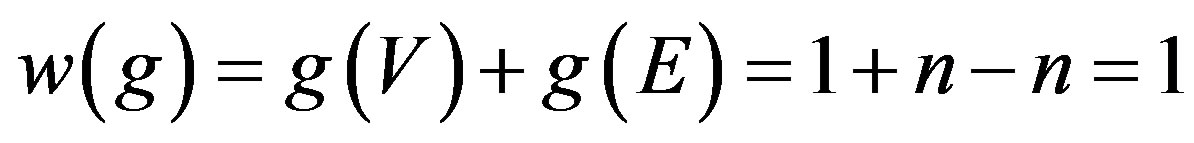 .
.
Thus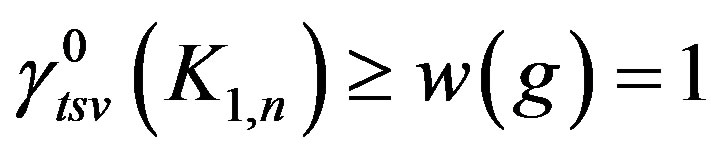 , which implies that
, which implies that 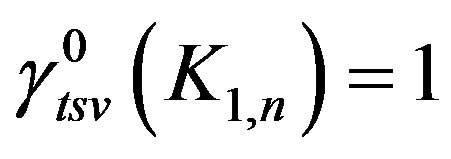 .
.
Propositon 5 For any circle ,
,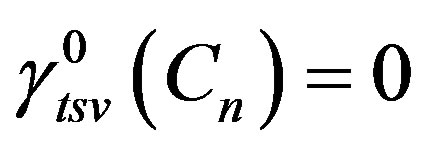 .
.
Proof. Let 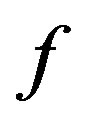 be a
be a 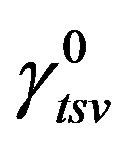 -function of
-function of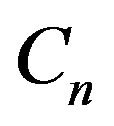 . Let
. Let
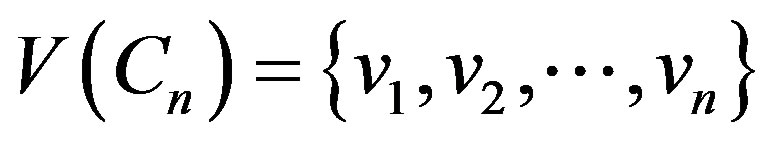 ,
,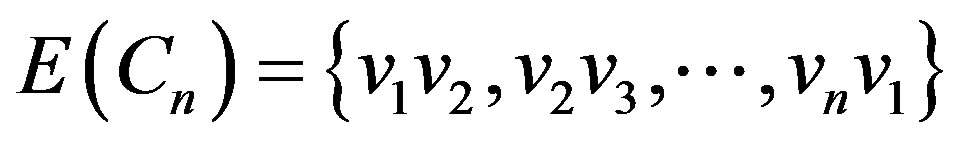 .
.
Since for every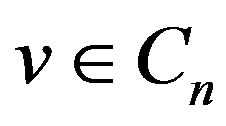 ,
,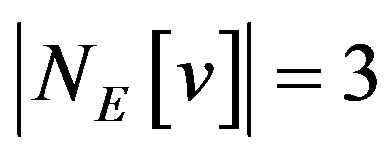 , we have
, we have
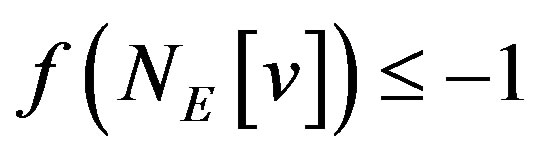 .
.
Thus
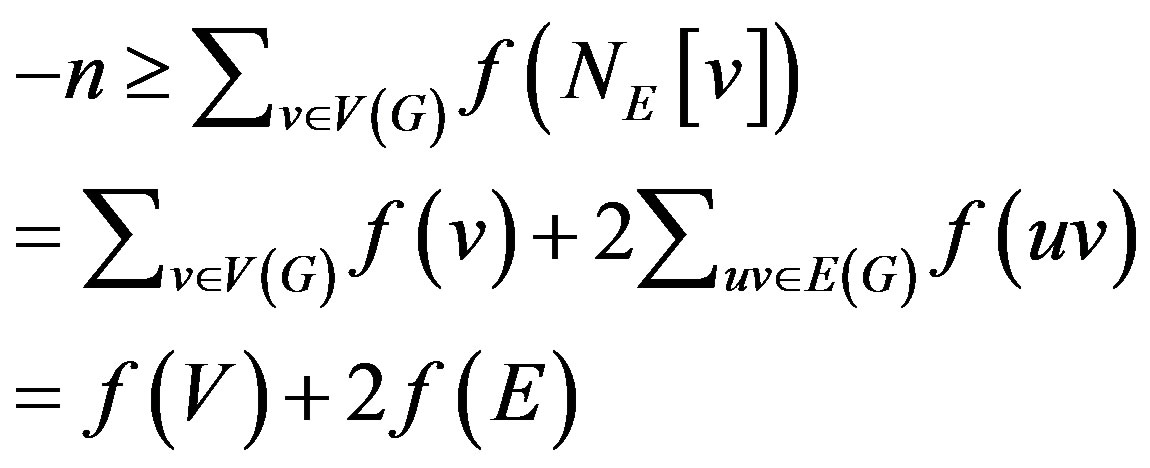 .
.
Therefore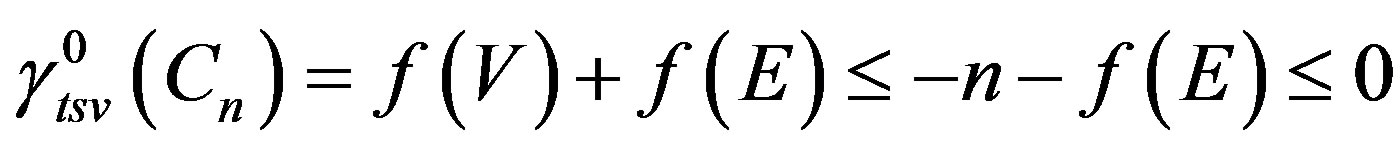 .
.
On the other hand, consider the mapping

 such that
such that
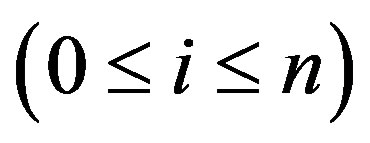
 ,
,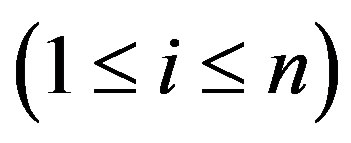
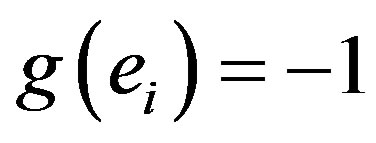 .
.
Then 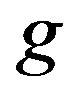 is a reverse total signed vertex dominating function on
is a reverse total signed vertex dominating function on 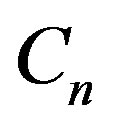 and
and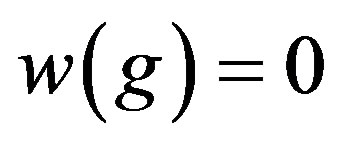 . Therefore
. Therefore
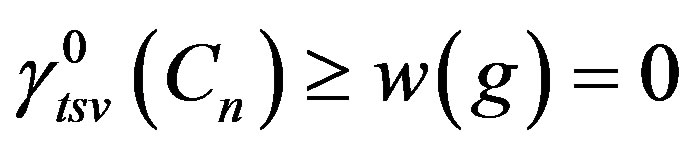 which implies
which implies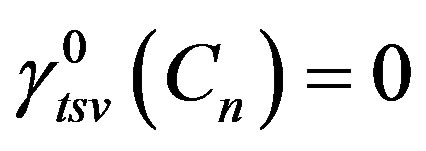 .
.
Propositon 6 For any complete bipartite graph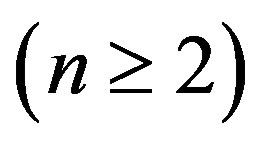
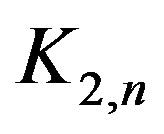 ,
,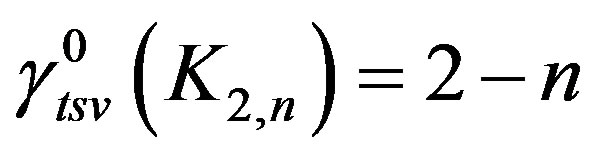 .
.
Proof. Let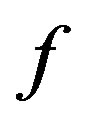 be a
be a 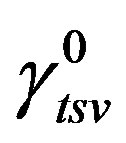 -function. Let
-function. Let
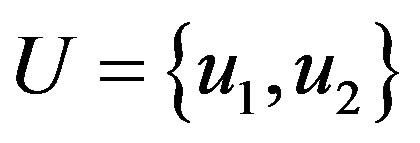 ,
, 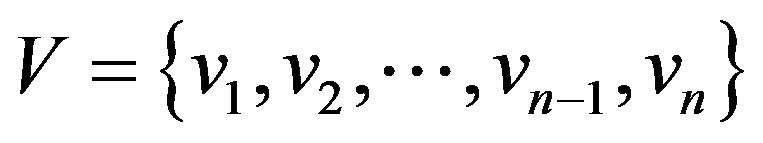 ,
,
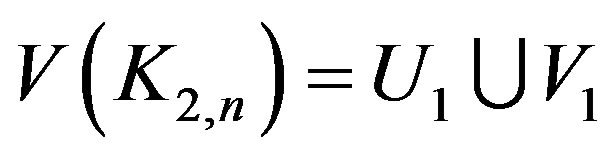
and
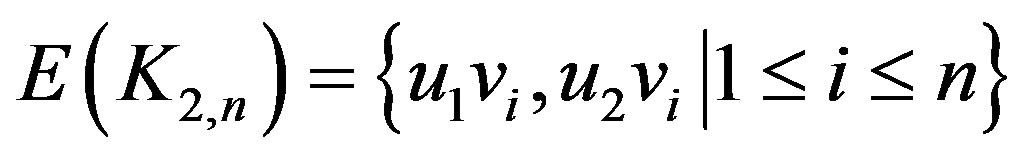 .
.
Since for every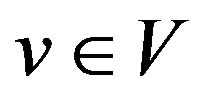 ,
, , we have
, we have 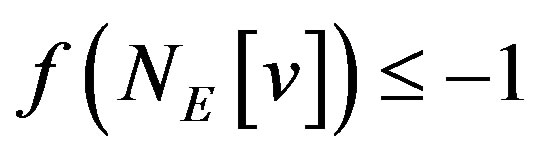 . Therefore
. Therefore
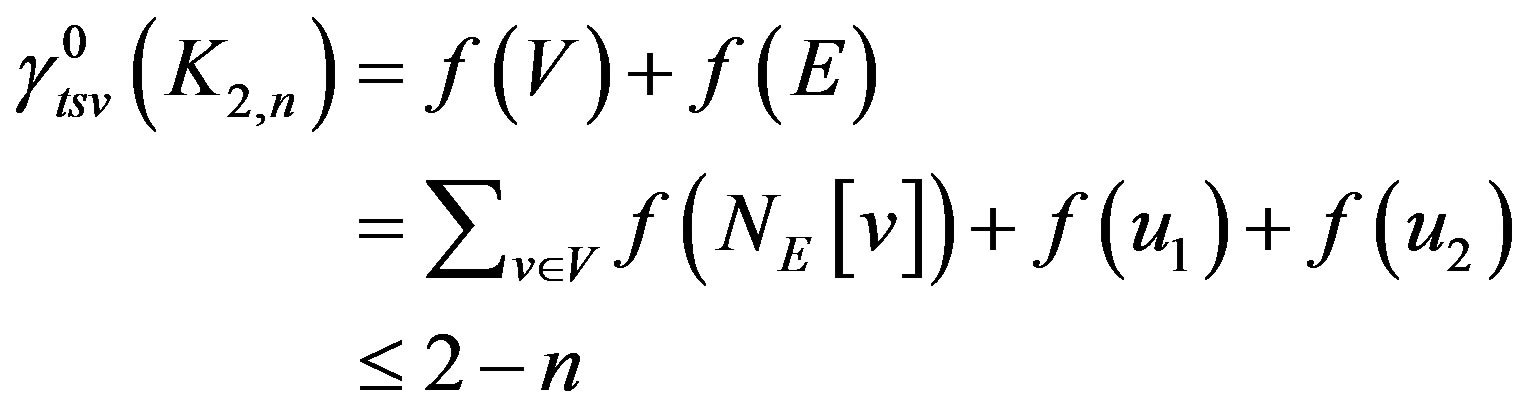 .
.
On the other hand, consider the mapping
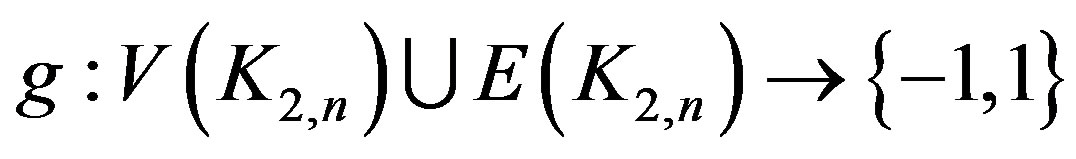
such that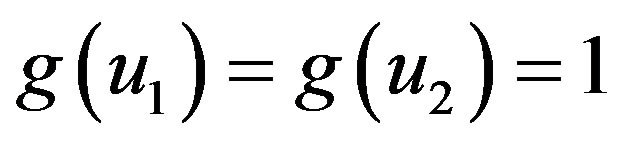 ,
, 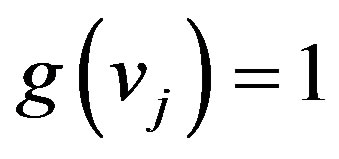 for
for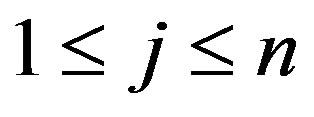 ,
,
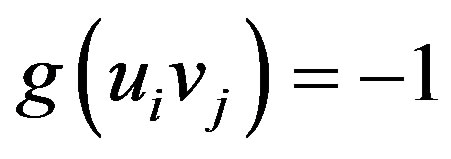 for
for 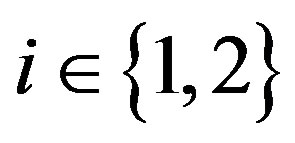 and
and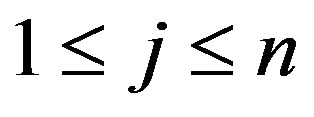 . Then
. Then 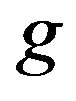 is a reverse total signed vertex dominating function on
is a reverse total signed vertex dominating function on 
and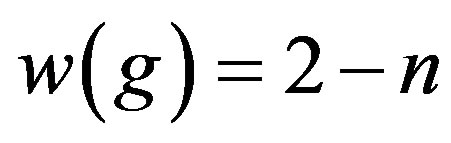 . Therefore
. Therefore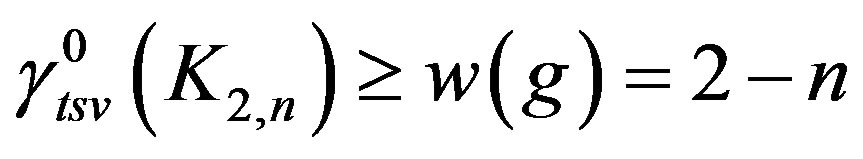 which implies
which implies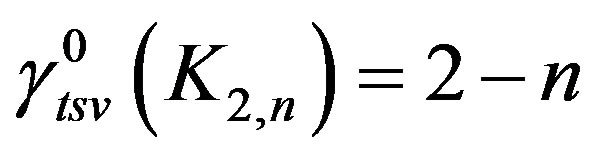 .
.
3. Acknowledgements
This work was supported by the Natural Science Foundation of Hebei Province (A2012408002), the Educational Commission of Hebei Province (ZH2011122, Z2011157) and Langfang Teachers College (LSZQ201106).
REFERENCES
- J. A. Bondy and V. S. R. Murty, “Graph Theory with Application,” Elsevier, Amsterdam, 1976.
- T. T. Chelvam and G. Kalaimurugan, “Bounds for Domination Parameters in Cayley Graphs on Dihedral Group,” Open Journal of Discrete Mathematics, Vol. 2, No. 1, 2012, pp. 5-10. doi:10.4236/ojdm.2012.21002
- T. W. Haynes, S. T. Hedetniemi and P. J. Slater, “Fundamentals of Domination in Graphs,” Marcel Dekker, New York, 1998.
- G. T. Wang and G. Z. Liu, “Rainbow Matchings in Properly Colored Bipartite Graphs,” Open Journal of Discrete Mathematics, Vol. 2, No. 2, 2012, pp. 62-64. doi:10.4236/ojdm.2012.22011
- J. E. Dunbar, S. T. Hedetniemi, M. A. Henning and P. J. Slater, “Signed Domination in Graphs,” Combinatorics, Graph Theory, Applications, Vol. 1, 1995, pp. 311-322.
- O. Favaron, “Signed Domination in Regular Graphs,” Discrete Mathematics, Vol. 158, No. 1, 1996, pp. 287- 293. doi:10.1016/0012-365X(96)00026-X
- Z. Zhang, B. Xu, Y. Li and L. Liu, “A Note on the Lower Bounds of Signed Domination Number of a Graph,” Discrete Mathematics, Vol. 195, No. 1, 1999, pp. 295-298. doi:10.1016/S0012-365X(98)00189-7
- X. Z. Lv, “Total Signed Domination Numbers of Graphs,” Science in China A: Mathematics, Vol. 37, 2007, pp. 573- 578.
- X. Z. Lv, “A Lower Bound on the Total Signed Domination Numbers of Graphs,” Science in China Series A: Mathematics, Vol. 50, 2007, pp. 1157-1162.

