Received 16 April 2016; accepted 26 June 2016; published 29 June 2016

ABSTRACT

In this paper, we discussed the problem of nonlocal value for nonlinear fractional q-difference equation. The classical tools of fixed point theorems such as Krasnoselskii’s theorem and Banach’s contraction principle are used. At the end of the manuscript, we have an example that illustrates the key findings.

Keywords:

Cauchy Problem, Fractional q-Difference Equation, Nonlocal Conditions, Fixed Point, Krasnoselskii’s Theorem

1. Introduction

Importance of fractional differential equations appears in many of the physical and engineering phenomena in the last two decades [1] - [3] . Problems with nonlocal conditions and related topics were studied in, for example [4] , and the nonlocal Cauchy problem [5] . The attention of researchers subject of q-difference equations appeared in recent years [6] [7] . Initially, it was developed by Jackson [8] [9] . Noted recently the attention of many researchers is in the field of fractional q-calculus [10] [11] . Recently nonlocal fractional q-difference problems have aroused considerable attention [12] [13] .

In this paper, we obtain the results of the existence and uniqueness of solutions for the Cauchy problem with nonlocal conditions for some fractional q-difference equations given by

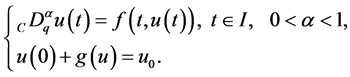(1)

Here, 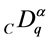is the Caputo fractional q-derivative of order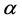, 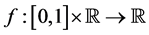and

are given continuous functions. It is worth mentioning that the nonlocal condition which can be applied effectively in physics is better than the classical Cauchy problem condition, see [14] .

Several authors have studied the semi-linear differential equations with nonlocal conditions in Banach space, [15] [16] . In [17] , Dong et al. studied the existence and uniqueness of the solutions to the nonlocal problem for the fractional differential equation in Banach space. Motivated by these studied, we explore the Cauchy problem for nonlinear fractional q-difference equations according to the following hypotheses.

(H₁) 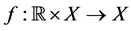is jointly continuous.

(H₂)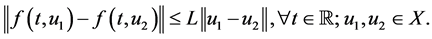

(H₃) 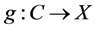is continuous and

(H₄) where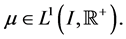

The problem (1) is then devolved to the following formula

(2)

See reference [18] for more details.

2. Preliminaries on Fractional q-Calculus

Let 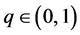and define

The q-analogue of the Pochhammer symbol was presented as follows

In general, if thereafter

The q-gamma function is defined by

and satisfies

The q-derivative of a function is here defined by

and

The q-integral of a function f defined in the interval is provided by

Now, it can be defined an operator, as follows

and

We can point to the basic formula which will be used at a later time,

where denotes the q-derivative with respect to variable s.

See reference [7] - [10] for more details.

Definition 2.1. [19] Let and f be a function defined on. The fractional q-integral of the Riemann-Liouville type is and

Definition 2.3. [19] The fractional q-derivative of the Caputo type of order is defined by

where is the smallest integer greater than or equal to.

Theorem 2.1. [20] Let and.Then, the following equality holds

Theorem 2.2. [18] [19] (Krasnoselskii)

Let M be a closed convex non-empty subset of a Banach space. Suppose that A and B maps M into X, such that the following hypotheses are fulfilled:

1) for all;

2) A is continuous and AM is contained in a compact set;

3) B is a contraction mapping.

Then there exists such that

3. Main Results

Now, the obtained results are presented.

Theorem 3.1.

Let (H₁)- (H₃) hold, if and, the problem (1) has a unique solution.

Proof. Define by

Choose and let. So, we can prove that, where

. For it, let and. Consequently, we find that

This shows that therefore,.

Now, for, we obtain

Thus

,

where

Thus, by the Banach’s contraction mapping principle, we find that the problem (1) has a unique solution.

Our next results are based on Krasnoselskii’s fixed-point theorem.

Theorem 3.2.

Let (H₁), (H₂), (H₃) with and (H₄) hold, then the problem (1) has at least one solution on I.

Proof. Take, and consider

Let A and B the two operators defined on P by

and

respectively. Note that if then

Thus

By (H₂), it is also clear that B is a contraction mapping.

Produced from Continuity of u, the operator is continuous in accordance with (H₁). Also we observe that

Then A is uniformly bounded on P.

Now, let and That’s where f is bounded on the compact set it means

We will get

which is autonomous of u and head for zero as Consequently, A is equicontinuous. Thus, A is relatively compact on P. Therefore, according to the Arzela-Ascoli Theorem, A is compact on P. Thus, the problem (1) has at least one solution on I.

Example 4.1 Consider the following nonlocal problem

(3)

where

Set

and

Let and Then we have

and

It is obviously that our assumptions in Theorem 3.1 holds with and for appropriate values of with and Indeed

(4)

Therefore the problem (3) has a unique solution on for values of and q sufficient stipulation (4). For illustration

・ If and then and

・ If and then and

Cite this paper

Maryam Al-Yami, (2016) A Cauchy Problem for Some Fractional q-Difference Equations with Nonlocal Conditions. American Journal of Computational Mathematics,06,159-165. doi: 10.4236/ajcm.2016.62017

References