American Journal of Computational Mathematics
Vol.05 No.02(2015), Article ID:57323,10 pages
10.4236/ajcm.2015.52014
Block Unification Scheme for Elliptic, Telegraph, and Sine-Gordon Partial Differential Equations
Samuel Jator
Department of Mathematics and Statistics, Austin Peay State University, Clarksville, TN, USA
Email: Jators@apsu.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 May 2015; accepted 19 June 2015; published 23 June 2015
ABSTRACT
In this paper, we use the method of lines to convert elliptic and hyperbolic partial differential equations (PDEs) into systems of boundary value problems and initial value problems in ordinary differential equations (ODEs) by replacing the appropriate derivatives with central difference methods. The resulting system of ODEs is then solved using an extended block Numerov-type method (EBNUM) via a block unification technique. The accuracy and speed advantages of the EBNUM over the finite difference method (FDM) are established numerically.
Keywords:
Extended Block Method, Elliptic and Hyperbolic PDEs, Method of Lines

1. Introduction
The method of lines approach which involves replacing the spatial derivatives with finite difference approximations is commonly used for solving PDEs; whereby, the PDE is transformed into systems of ODEs and solved by reliable ODE solvers (see Lambert [1] , Ramos and Vigo-Aguiar [2] , Brugnano and Trigiante [3] , D’Ambrosio and Paternoster [4] , and). Our objective is to convert the elliptic and hyperbolic PDEs into systems of ODEs by replacing the appropriate derivatives with central difference methods. The resulting systems of ODEs are then solved using an EBNUM via a block unification technique. We consider the two-dimensional PDE
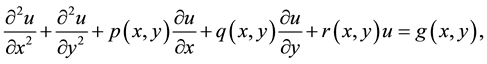 (1)
(1)
subject to Dirichlet or Neumann boundary conditions, where
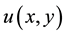 denotes the dependent variable, x and y are spatial variables,
denotes the dependent variable, x and y are spatial variables,
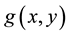 is a distributed source, and when
is a distributed source, and when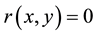 , (1) becomes the two-dimensional convection diffusion equation given in Sun and Zhang [5] . We note that for
, (1) becomes the two-dimensional convection diffusion equation given in Sun and Zhang [5] . We note that for
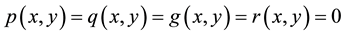 (1) is the Laplace equation, for
(1) is the Laplace equation, for
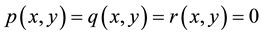 (1) is the Poisson equation, and for
(1) is the Poisson equation, and for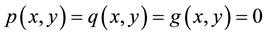 , (1) becomes the Helmoltz equation. The Sine- Gordon and telegraph equations can also be obtained from (1) by obvious notational modifications.
, (1) becomes the Helmoltz equation. The Sine- Gordon and telegraph equations can also be obtained from (1) by obvious notational modifications.
We invoke the method of lines approach in which for real numbers , we seek a solution in the strip
, we seek a solution in the strip
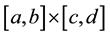 by first fixing the grid in the spatial variable x; then, approximating this spatial derivative using central difference methods, and finally solving the resulting system of second order time independent ODEs in the spatial variable y. Specifically, we discretize the x variable such that with mesh spacings
by first fixing the grid in the spatial variable x; then, approximating this spatial derivative using central difference methods, and finally solving the resulting system of second order time independent ODEs in the spatial variable y. Specifically, we discretize the x variable such that with mesh spacings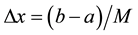 ,
,
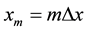 ,
,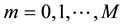 .
.
We then define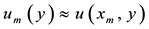 ,
,
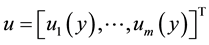 ,
,
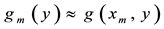 ,
,
 , and replace the partial derivatives
, and replace the partial derivatives
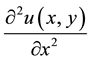 and
and


The problem (1) then leads to the resulting semi-discrete problem

which can be written in the form

subject to the boundary conditions

where


The paper is organized as follows. In Section 2, we derive a continuous linear multistep method (LMM) which is used to formulate the EBNUM. The computational aspects of the method are given in Section 3. Numerical examples are given in Section 4 to show the accuracy of the method. Finally, the conclusion of the paper is discussed in Section 5.
2. Continuous LMM and EBNUM
In this section, we derive a continuous representation of a LMM which is used to generate the EBNUM. On the interval


where








If the function (4) satisfies the scalar form of the differential Equation (3) at the points

Thus, Equations (5) and (6) lead to a system involving the following five equations

which is solved with the aid of Mathematica to obtain


where




The EBNUM is then obtained by evaluating (7) at



Remark 1 We note that the first two members of (9) were given in [7] and used for solving the special second order initial value problem.
The order of each method in (9) is given by the vector


The method (9) can be expressed in block form as

where the positive integer










given by the coefficients of (9).
Let the local truncation error be defined by

where




Theorem 2 Let









Proof. See Jator [8] .
Stability
The linear-stability of (11) is discussed by applying the method to the test equation



where the matrix

Definition 3 Let










Remark 4 We found that



which is twice the stability interval of the standard Numerov method. In this case, the interval of stability is the same as the interval of periodicity.
3. Computational Aspects via Block Unification
Recall that the semi-discretization of (1) is initially performed on the partition



Next, we summarize the block unification algorithm. Let



Step 1: Use the block extension of (11) for










Step 2: The blocks are unified to form a system given by

Step 3: The solution of (1) is approximated by the solutions in step 2 as

We emphasize that the block unification technique leads to a single matrix of finite difference equations, which is solved to provide all the solutions of (1) on the entire grid given by the rectangle
4. Numerical Examples
4.1. Elliptic PDEs
In this subsection, the performance of the EBNUM is tested on five problems, which include the Poisson equation, Laplace equation subject to Neumann boundary conditions, Laplace equation subject to Dirichlet boundary conditions, Helmoltz equation, and the two-dimensional convection diffusion equation. In all the figures, the EBNUM is represented by uapprox and the exact solution is represented by uexact.
Example 5 As our first test example, we solve the given Poisson equation (see Burden and Faires [11] ).



The exact solution is given by
This example was chosen to demonstrate that the EBNUM can be used to solve the Poisson equation with Dirichlet boundary conditions. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 1.
Example 6 As our second test example, we solve the given Laplace equation subject to Neumann boundary conditions (see Zill and Cullen [12] ).



The exact solution is given by
This example was chosen to illustrate that the EBNUM is cable of solving the Laplace equation with Neumann boundary conditions. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 2.
Example 7 As our third test example, we solve the given Laplace equation subject to Dirichlet boundary conditions (see Zill and Cullen [12] ).


Figure 1. Approximate and exact solutions for example 4.1, h = 1/64; Δx = 1/64.

Figure 2. Approximate and exact solutions for example 4.2, h = 1/128; Δx = 1/128.


The exact solution is given by

This example was chosen to demonstrate the performance of the EBNUM on the Laplace equation with Dirichlet boundary conditions. We truncated the exact solution at 50, since the exact solution is an infinite series. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 3.
Example 8 We consider the given two-dimensional Helmoltz equation (see Cheney [13] ).

The exact solution is given by
The Dirichlet boundary conditions are chosen accordingly. This example was chosen to demonstrate that the EBNUM can be used to solve the Helmoltz equation. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 4.
Example 9 We consider the given two-dimensional convection diffusion equation (see Sun and Zhang [5] ).


Figure 3. Approximate and exact solutions for example 4.3, h = 1/128; Δx = 1/128.
The exact solution is given by



The Dirichlet boundary conditions and


Figure 4. Approximate and exact solutions for example 4.4, h = 1/128; Δx = 1/128.

Figure 5. Approximate and exact solutions for example 4.5, h = 1/128; Δx = 1/128.
4.2. Hyperbolic PDEs
Example 10 We consider the following one-dimensional nonlinear undamped Sine-Gordon equation given in Dehghan and Shokri [14] )



The exact solution is given by
C is the velocity of the solitary wave, and the boundary conditions are given according. The problem is solved for


Example 11 We consider the given Telegraph equation (see Ding et al. [15] ).


Figure 6. Approximate and exact solutions for example 4.6, h = 1/50; Δx = 1/150.
The exact solution is given by
The boundary conditions are chosen accordingly. This example was chosen to demonstrate that the EBNUM can be used to solve the telegraph equation. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 7.
4.3. Comparison of EBNUM and FDM
In this subsection, we compare the errors


5. Conclusion
A block unification method based on the EBNUM is proposed and applied to elliptic and hyperbplic PDEs via the method of lines technique. It is shown that the method is very flexible as it can be applied to solve a variety of elliptic and hyperbolic PDEs with either Dirichlet or Neumann boundary conditions. The method is also shown to have both accuracy and speed advantages when compared with the FDM (see Table 1). Our future re-

Figure 7. Approximate and exact solutions for example 4.7, h = 1/16; Δx = 1/16.
Table 1. Comparison of errors and CPU time in seconds.
search will be to search for higher order LMMs that can solve the general forms of elliptic and hyperbolic PDEs.
References
- Lambert, J.D. (1973) Computational Methods in Ordinary Differential Equations. John Wiley, New York.
- Vigo-Aguiar, J. and Ramos, H. (2007) A Family of A-Stable Collocation Methods of Higher Order for Initial-Value Problems. IMA Journal of Numerical Analysis, 27, 798-817. http://dx.doi.org/10.1093/imanum/drl040
- Brugnano, L. and Trigiante, D. (1998) Solving Differential Problems by Multistep Initial and Boundary Value Methods. Gordon and Breach Science Publishers, Amsterdam.
- D’Ambrosio, R. and Paternoster, B. (2014) Numerical Solution of a Diffusion Problem by Exponentially Fitted Finite Difference Methods. Springer Plus, 3, 425-431. http://dx.doi.org/10.1186/2193-1801-3-425
- Sun, H. and Zhang, J. (2004) A High Order Finite Difference Discretization Strategy Based on Extrapolation for Convection Diffusion Equations. Numerical Methods for Partial Differential Equations, 20, 18-32. http://dx.doi.org/10.1002/num.10075
- Jator, S.N. (2008) A Class of Initial Value Methods for the Direct Solution of Second Order Initial Value Problems. International Journal of Pure and Applied Mathematics, 46, 225-230.
- Adee, S.O., Onumanyi, P., Sirisena, U.W. and Yahaya, Y.A. (2005) Note on Starting the Numerov Method More Accurately by a Hybrid Formula of Order Four for an Initial Value Problem. Journal of Computational and Applied Mathematics, 175, 369-373. http://dx.doi.org/10.1016/j.cam.2004.06.016
- Jator, S.N. and Li, J. (2012) An Algorithm for Second Order Initial and Boundary Value Problems with an Automatic Error Estimate Based on a Third Derivative Method. Numerical Algorithms, 59, 333-346. http://dx.doi.org/10.1007/s11075-011-9492-3
- Coleman, J.P. and Ixaru, L.G.R. (1996) P-Stability and Exponential-Fitting Methods for . IMA Journal of Numerical Analysis, 16, 179-199. http://dx.doi.org/10.1093/imanum/16.2.179
- Coleman, J.P. and Duxbury, S.C. (2000) Mixed Collocation Methods for . Journal of Computational and Applied Mathematics, 126, 47-75. http://dx.doi.org/10.1016/S0377-0427(99)00340-4]
- Burden, R.L. and Faires, J.D. (1985) Numerical Analysis. 3rd Edition, Prindle, Weber and Schmidt, Boston.
- Zill, D.G. and Cullen, M.R. (2001) Differential Equations with Boundary-Value Problems. 5th Edition, Brooks/Cole, California.
- Cheney, W. and Kincaid, D. (1985) Numerical Mathematics and Computing. Brooks/Cole, California.
- Dehghan, M. and Shokri, A. (2008) A Numerical Method for One-Dimensional Nonlinear Sine-Gordon Equation Using Collocation and Radial Basis Functions. Numerical Methods for Partial Differential Equations, 24, 687-698. http://dx.doi.org/10.1002/num.20289
- Ding, H., Zhang, Y., Cao, J. and Tian, J. (2012) A Class of Difference Scheme for Solving Telegraph Equation by New Non-Polynomial Spline Methods. Applied Mathematics and Computation, 218, 4671-4683. http://dx.doi.org/10.1016/j.amc.2011.10.078


