American Journal of Computational Mathematics
Vol.3 No.4(2013), Article ID:41062,6 pages DOI:10.4236/ajcm.2013.34046
Analysis and Characterization of Flow-Generated Sound
An-Institut Fluidund Pumpentechnik Merseburg, Geusaer Straße, Merseburg, Germany
Email: dominik.surek@hs-merseburg.de
Copyright © 2013 Dominik Surek. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 19, 2013; revised September 21, 2013; accepted October 1, 2013
Keywords: Fluid Flow; Fluids; Akustics; Spectrum; Wavelets
ABSTRACT
Flow-generated sound and velocity distributions of free flows are characterized by frequency spectra (FFT and several spectra from the octave spectrum over the one-third octave spectrum till the narrow band spectrum), by the PSD (power spectrum density) and wavelets. Whereas previously, flow processes are characterized by the average velocity, by the local velocity, if needed also by the three-dimensional velocity distribution and the degree of turbulence, also the flows and particular velocity distributions could be described by the acoustic pressure and level, by the power spectrum density and by wavelets, especially by the Gabor-Wavelet, as shown below.
1. Introduction
Velocities of air and gas flows and their frequency of the sound pressure oscillation are coupled together by the Strouhal number Sr = fd/c. The range of the Strouhal number, in dependence of the Reynolds number Re = cd/ν, can be divided into a subcritical section Sr = 0.10 to 0.18, in the Reynolds number range Re = 60 to 3 × 105 into a critical range from Re = 2 × 105 bis 5 × 106 and into a supercritical range with values of Sr = 0.28 at Reynolds numbers of Re = 5 × 106. This context is successfully used in the manufacture of musical instruments and plucked instruments industry. It can be used successfully in other technical areas, in particular in the field of flow measurement as described below. In a gas and liquid flow, nothing is constant except for the postulated mean values of the velocity and pressure. The sound pressure and the sound pressure level as well as the velocity change with high frequency from f = 10 Hz to 100 kHz, but also into lower ultrasonic range. The frequencies are caused by the turbulence of the flow, which is characterized by the degree of turbulence. The degree of turbulence of a flow is defined by the speed of variations in the three coordinate directions of a Cartesian coordinate system.
2. Flow Velocity and Frequency of the Sound Pressure Oscillation
So far, flows and leakage flows as shown in Figure 1
and velocity distributions by the local velocities are described by the average values and the turbulent fluctuations in addition by the degree of freedom [1,2]. For the description of the energy distribution of a turbulent flow, which is a function of the wavelength or the frequency of the turbulent vortices, the energy spectrum with the energy spectral density E in dependence on the wavelength λ or wave number k [3-5]. The wave number or vortex number k = ω/c = 2π/λ is a ordinal number for the transfer of energy from large to small turbulence numbers. The flow of energy in turbulent flows is directed to larger wave numbers k (Figure 2). This form of energy transfer is the reason why the frictional resistance in turbulent flows and the distribution of the average velocity is only weakly dependent on the Reynolds number. The pressure losses in turbulent flows are mainly caused by the vortex viscosity. Going one step further in the description of the flow, we come to the spectral analysis of the flow. Spec-

Figure 1. Outflow.

Figure 2. Energy spectrum as function of the wave number.
tral analysis of the flow means the separation of the input signal of the flow into a series of sinusoidal and cosinusoidal oscillations. Each oscillation has its own frequency, amplitude and phase. The sum of sine and cosine waves is called the spectrum of which there are many. Well known are time signals (Figure 3) and the frequency spectra, which can be determined using the Fourier transform. Figure 4 shows the frequency spectra of three very similar time signals from Figure 3 for the times t = 1s with 200,000 measured values, t = 0.1 s with 20,000 measured values and for t = 10 ms with 2000 measured values. The following results outline the acoustic data such as the acoustic pressure, the acoustic pressure spectra, specific spectra and the sound pressure level.
3. Sound Pressure Spectra of Air Outflow
In the following the acoustic effects of air outflow form a pressure vessel through defined outlet openings according to Figure 1 are analyzed and outlined. The outlet openings are d = 1.6 mm to d = 18.4 mm with the exit areas A = 2.0 mm2 to A = 265.9 mm2. The outflow from the pressure vessel is carried out at p = 0.25 bar to p = 5bar with outlet velocities of c = 12 m/s up to c = 48 m/s. In Figure 5 the frequency spectra (FFT) for two outlet openings of d = 10 mm and d = 18.4 mm for the tank pressures of p = 1.5 bar to 5.0 bar shown. In Figure 5 is seen that the amplitudes at pressures of p = 4.0 bar and p = 4.5 bar with Lp = 0.74 mPa und Lp = 0.68 mPa take maximum values and that also the outlet opening has a strong influence on the spectral distribution. The amplitudes of the frequency spectra at the pressures p = 4.0 bar and p = 4.5 bar at the frequencies of f = 5 kHz, 8 kHz, 13 kHz und f = 24 kHz are relative maximum values. The frequency spectra of the flow-generated sound extend to the ultrasonic range to about f = 100 kHz, but the significant amplitudes for the pressures from p = 3.0 bar up to p = 5.0 bar extend to the frequency f = 60 kHz. This distribution of the spectra is also set for the other pressures and other outlets.
Examining the octave spectra, the third octave spectra as 1/3-octave spectrum, as well as narrow-band spectra,

Figure 3. Time signals of a measurement for the three measurement times from t = 1 s to t = 10 ms.

Figure 4. Fast Fourier transforms (FFT) of the sound pressure for the three measurement times.
the 1/24-octave spectrum and 200 Hz narrowband spectrum for the sound pressure pSch and picture these spectra for comparison in Figure 6, so you can find the following results.
- The flow-generated sound occurs in a frequency range of f = 1 kHz to 80 kHz. They start in the audible range and extend into the ultrasound range.
- The octave spectrum is roughly structured and shows two maximum values of Lp = 6.4 mPa at f = 8 kHz and Lp = 7.6 mPa at 32 kHz.
- The third octave spectrum in Figure 6 with lower amplitudes of Lp = 4.4 mPa at f = 8 kHz and with Lp = 6.4 mPa at the frequency of f = 26 kHz is structured finer. The minimum point of the octave spectrum with Lp = 6.0 mPa at f = 17.5 kHz forms a relative amplitude maximum of Lp = 4.0 mPa.
- The two narrow band spectra for the 1/24-octave spectrum and for the 200 Hz narrow band spectrum, which are very similar, are designed differently. Both narrow band spectra form four maximum values at the frequencies f = 5.6 kHz; f = 8.8 kHz; f = 15 kHz

Figure 5. Fast Fourier transforms (FFT) of the sound pressure for the pressures from p = 1.0 bar up to 5.0 bar at d = 10 mm and d = 18.4 mm.
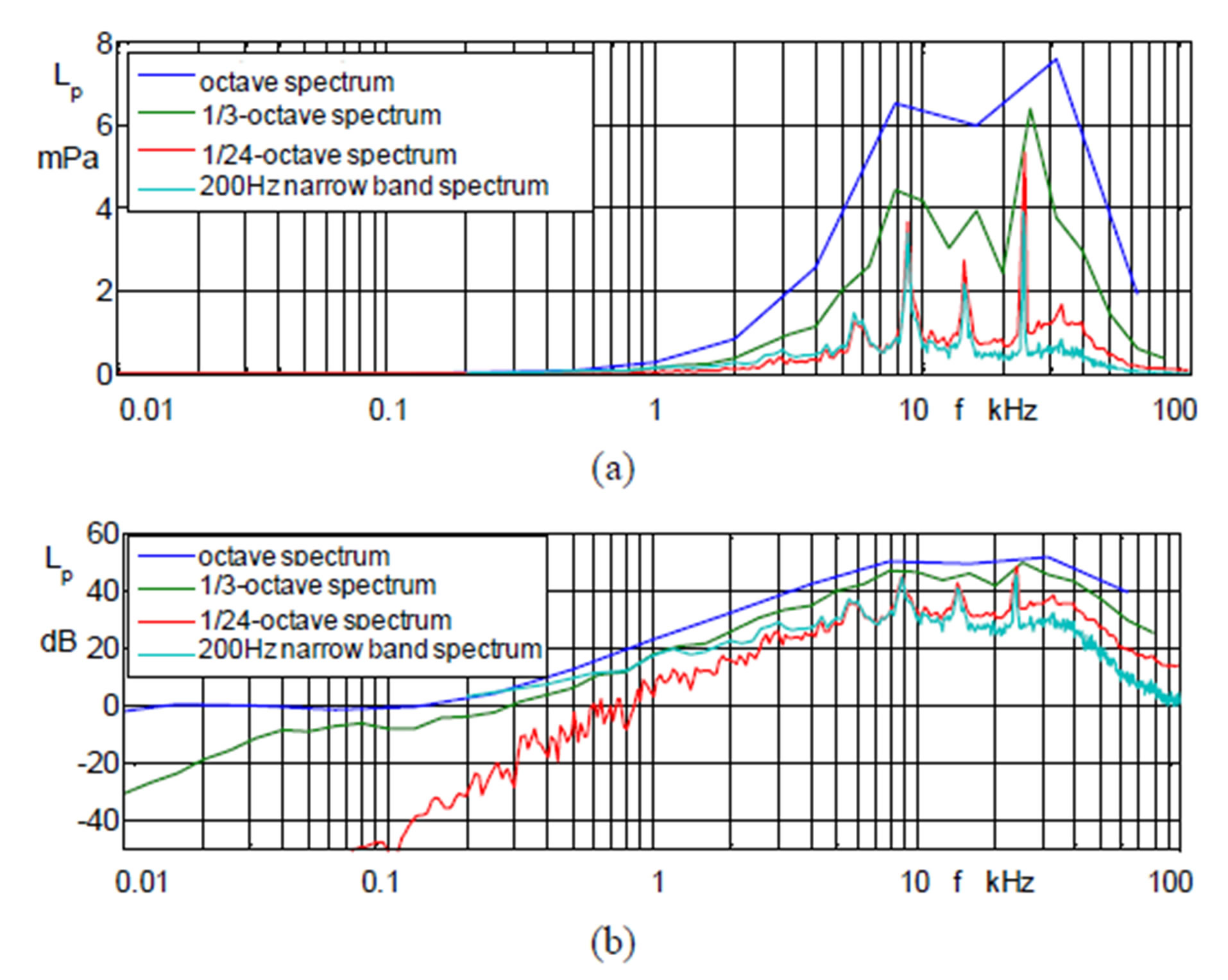
Figure 6. Spectra of the sound pressure (a) and of the pressure level (b) for the octave spectrum till the narrow band spectrum for d = 2 mm, L = 12 mm and p = 5 bar.
and f = 23 kHz, but the three last-mentioned maximum values greatly protrude with the maximum amplitudes of Lp = 5.4 mPa and Lp = 4.0 mPa, already clearly point out the finer vortex structure of the turbulent outflow and the quadrupole source in the inhomogeneous wave equation of Lighthill [4-6].
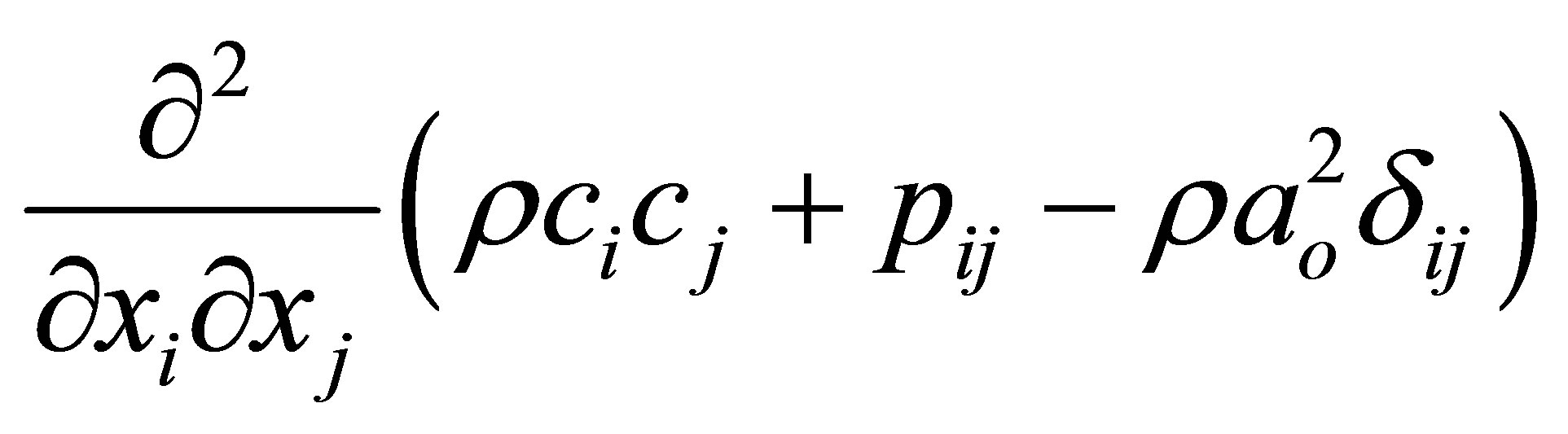
The expression  is called Lighthill tensor. The pressure oscillations per unit volume described by the Lighthill tensor represents a field of stress fluctuations.
is called Lighthill tensor. The pressure oscillations per unit volume described by the Lighthill tensor represents a field of stress fluctuations.
If these four spectra of the sound pressure are shown as sound pressure level in the same Figure 6, this results in a different form. In the representation of sound pressure level, which extends from Lp = −45 dB to 52 dB, the sound pressure levels in the lower frequency range of f = 10 bis 1000 Hz are greatly increased. Thus, the amplitudes of the pressure level obtained in the frequency range from f = 1 Hz to 1000 Hz far greater importance, while the level values of the octave and third-octave spectrum are zero and only from the frequency f = 150 Hz take positive values. On the other hand the peak values of sound pressure level in the range of f = 5.5 to 100 kHz are strongly attenuated. They are easily highlighted only in the narrow-band spectra. In spectral analysis so both forms of representation, the sound pressure spectra as well the level representation should be used.
Comparing the narrow band spectra (1/24 octave spectrum) for the outlet openings with the opening widths d = 1 to 5 mm and pressure values of p = 2 bar and p = 3 bar in Figure 7, we obtain the following results. At the pressure of p = 2 bar for the opening d = 5 mm is a obvious maximum amplitude of Lp = 0.83 mPa at the frequency f = 6.2 kHz. The maximum amplitude of all other openings from d = 1 mm up to d = 3 mm does not exceed the amplitude value of Lp = 0.52 mPa, while the frequencies reach the range between f = 3 kHz and 24 kHz. The results at the pressure of p = 3.0 bar behave similar. The frequency band extend from f = 3 kHz to 60 kHz, but the

Figure 7. Comparing the 1/24 octave spectra of the sound pressure for openings of d = 1 mm up to 5 mm and pressures of p = 2.0 bar (a) and 3.0 bar (b).
amplitude values of the sound pressure assume larger values.
4. Spectrogram and Power Spectrum Density (PSD)
In addition to the FFT and the spectra, also the spectrograms provide a good insight into the spectral distribution of the flow acoustics and into the turbulence of the flow. The spectrogram is a color-scaled representation of the 200-Hz narrow-band spectrum as Figure 8 shows. In the Figure 8(a) is the spectrogram for the opening of d = 1mm and L = 12 mm and the pressure p = 3 bar and in Figure 8(b) is the spectrogram for d = 2 mm and L = 12 mm for the expansion pressure of p = 5 bar shown, where the four amplitude lines extend over the entire period of t = 1 s. Only the fifth spectral line at f = 34 kHz is discontinuous and shifts in time from f = 27 kHz to 34 kHz. The spectrogram for p = 3 bar in Figure 8(a) is much more homogeneous, with five dark brown spectral lines between f = 1.5 kHz and f = 34 kHz visible. The amplitude level is determined by the color scale ai = 0 bis 120.
In Figure 9 the power spectrum density plots are shown in linear and logarithmic scale for the opening diameter of d = 2 mm and p = 5 bar (Figure 9). In Figure 9 you can see the outstanding amplitudes at frequencies of f = 5.7 kHz, f = 8.7 kHz, f = 14.4 kHz and f = 23.9 kHz. Similar to the representation of the sound pressure level in logarithmic scale, also the amplitudes in the frequency range f = 0.01 kHz to 10 kHz in the logarithmic representation of the power spectrum density are greatly extended and so the lower frequency range is very clear. To make the power spectrum density over the entire frequency range significantly, both forms of representation are recommended.
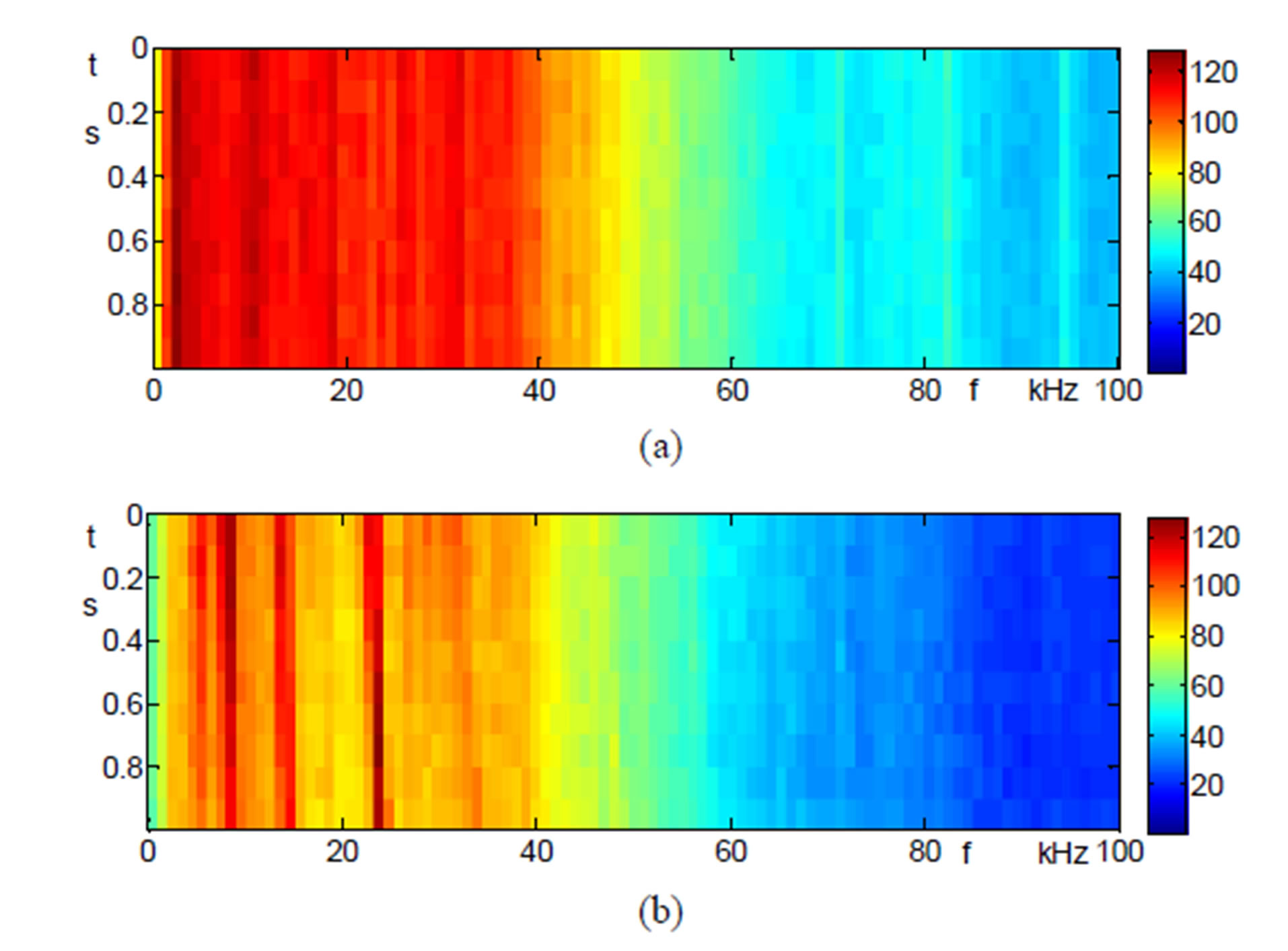
Figure 8. (a) Spectrogram for the diameter d = 1 mm, L = 12 mm and pressure p = 3 bar; (b) Spectrogram for the diameter d = 2 mm, L = 12 mm and pressure p = 5 bar.

Figure 9. Power spectral density in linear and logarithmic scale for d = 2 mm, L = 12 mm and p = 5 bar.
5. Wavelets of the Discrete Wavelet Transform
The predetermined functions in a continuous or discrete wavelet transformation are called wavelets. They generalize the short-time Fourier transforms. In contrast to sine and cosine functions of the Fourier transform, the wavelets have not only a location in the frequency spectrum, but also in the time domain and thereby open up new areas of the signals. The integral of the wavelet function is always zero. There are different wavelets from the Daubechies wavelet on the Morlet wavelet to the Gabor wavelet. With the two-dimensional Gabor wavelet the following results of the flow-generated sound can be represented. In Figures 10 to 13 the plane and spatial Gabor wavelets for five different measuring points in the plane and spatial representation are given. In both representations the interlocking of the frequency ranges of sound pressure oscillations is seen. The Gabor wavelets in Figures 10 to 13 show very clearly the magnitude of the amplitude of the sound pressure oscillation with values up to 75 dB. Figure 10 shows the planar end threedimensional Gabor wavelet for the diameter d = 1.6 mm and the pressure p = 5 bar. The time and the frequency dependence of the different amplitudes, which are not continuous and run compliant with the random variables of the time signals, can be seen in Figure 10. In Figure 10(b) the frequency tracks which extend over the measurement time can be seen. These frequency tracks can also be seen in the planar representation of the Gabor wavelet in Figure 11(a) at the frequencies f = 10 kHz, f = 15 kHz und 26 kHz, which extend over the entire time. In the three-dimensional representation of the Gabor wavelet are also the maximum amplitudes seen (Figure 11(b)). In Figure 12 the planar and three-dimensional representation of the Gabor wavelets for d = 3 mm and p
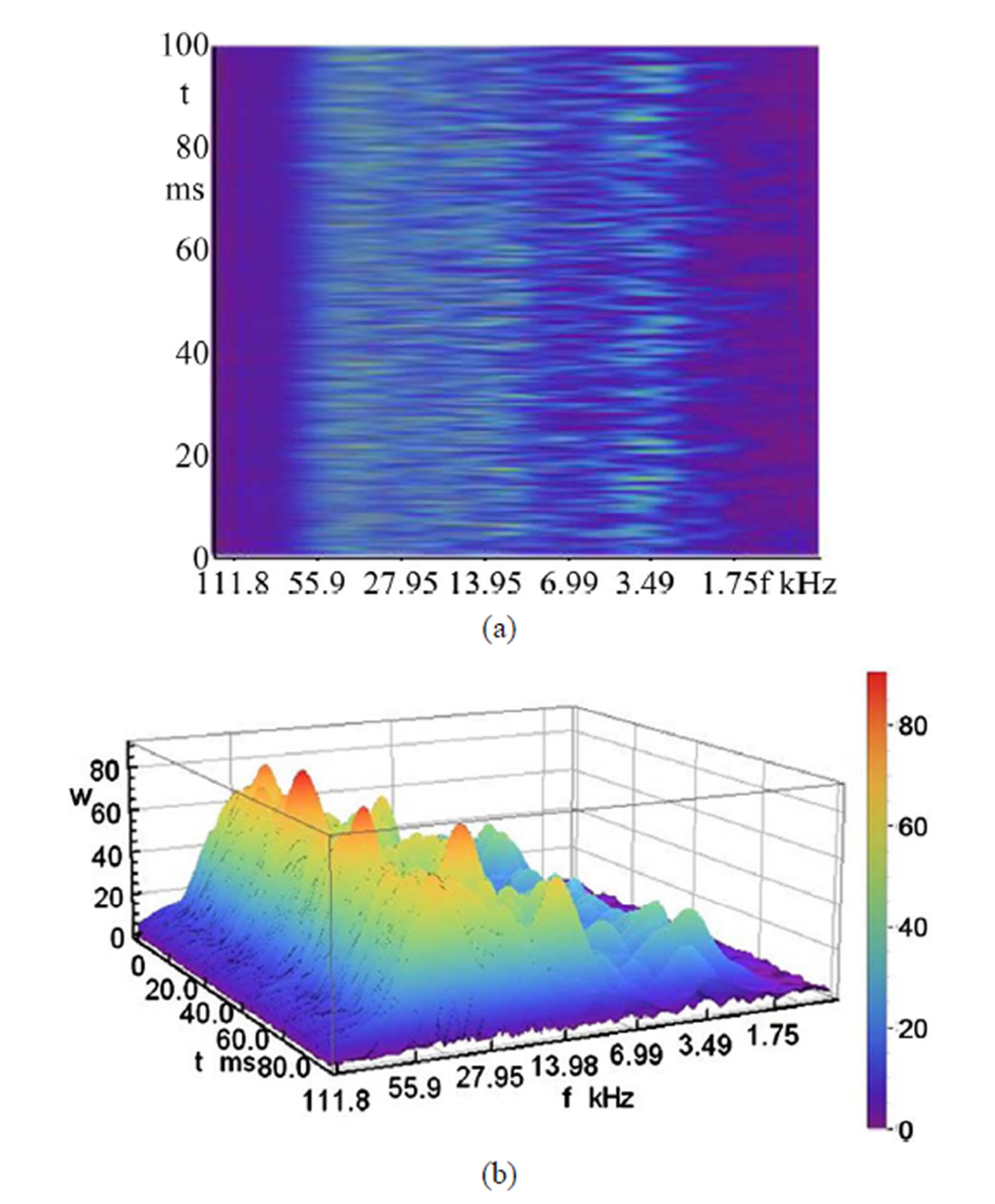
Figure 10. Plane and three-dimensional Gabor wavelet for the sound pressure at d = 1.6 mm and p = 5 bar.

Figure 11. Plane and three-dimensional Gabor wavelet for the sound pressure at d = 2.0 mm and p = 5 bar.
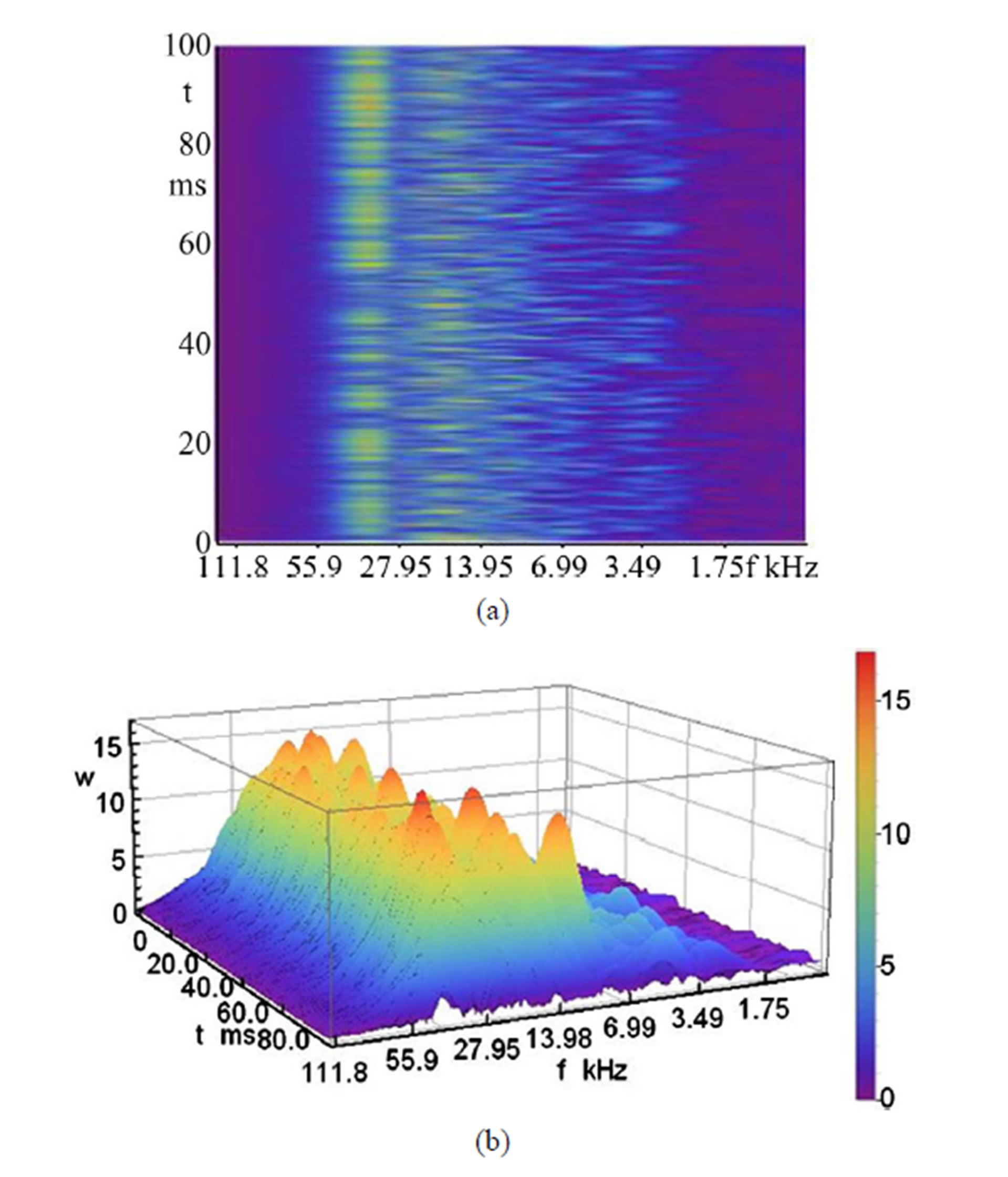
Figure 12. Plane and three-dimensional Gabor wavelet for the sound pressure at d = 3 mm and p = 4.25 bar.
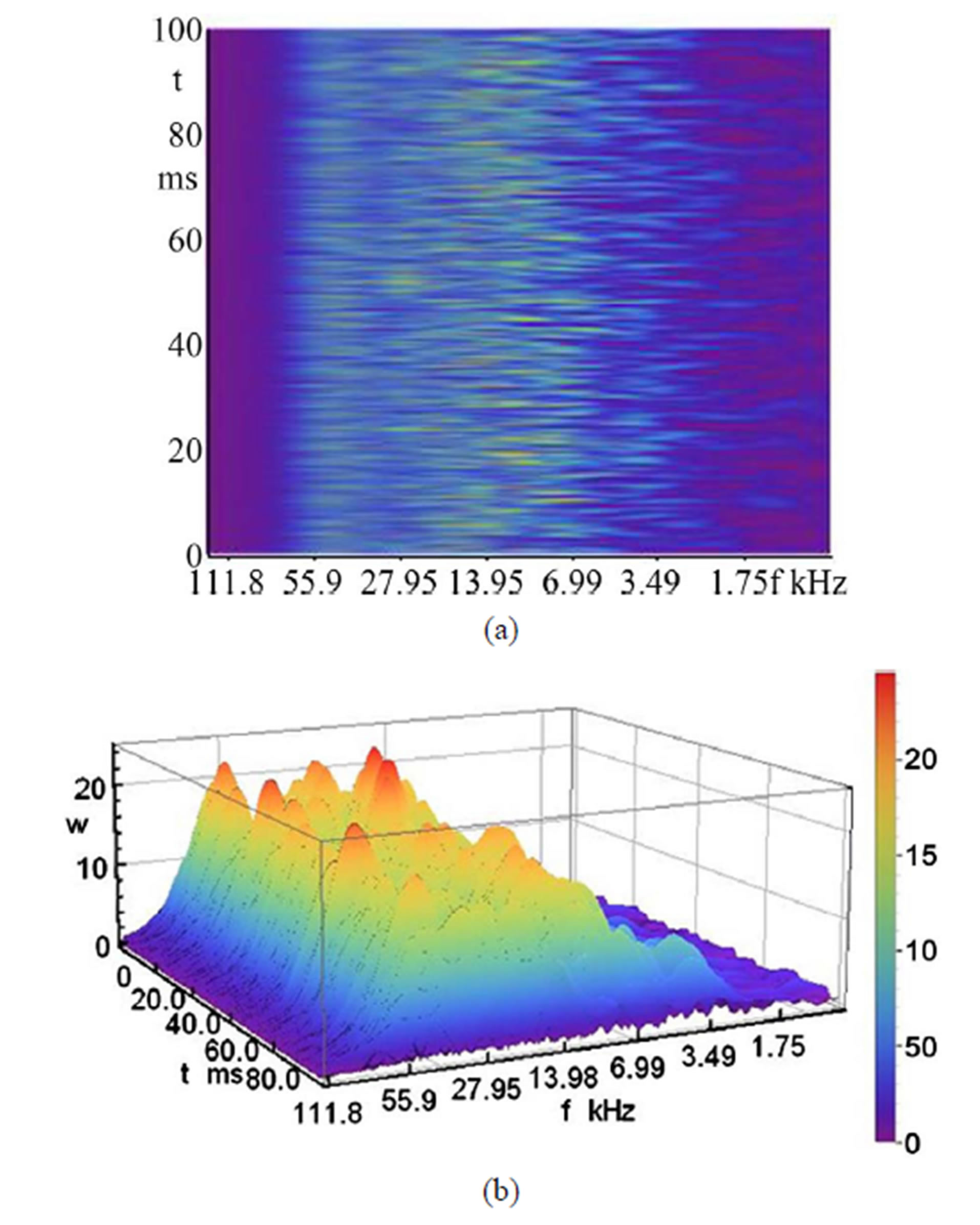
Figure 13. Plane and three-dimensional Gabor wavelet for the sound pressure at d = 4 mm and p = 5 bar.
= 4.25 bar are shown. Here again the traces of the two maximum values in the planar representation is visible. The 3-D display shows the large number of maximum values in the two frequency tracks. The frequency range extends from f = 3 kHz to about 32 kHz, so the results of the octave and narrow-band spectra have been confirmed. In Figure 13 are the plane and the 3-D wavelets for the opening diameter of d = 4 mm and p = 5.0 bar visible with two distinct frequency tracks.
6. Summary
The advanced new forms of Fourier transform as the spectrograms, the power spectral density and the wavelet transforms provide a deeper insight into the energy transport of the turbulent flow and in the spectra of the vortex turbulence of gas and air flows.
REFERENCES
- E. Truckenbrodt, “Fluidmechanik,” Springer-Verlag, Berlin, 1989.
- H. C. Kuhlmann, “Strömungsmechanik,” Pearson, München, 2007.
- D. Surek and S. Stempin, “Angewandte Strömungsmechanik,” Teubner Verlag, Wiesbaden, 2007. http://dx.doi.org/10.1007/978-3-8351-9094-8
- D. Surek, “Strömungsvorgänge und Schwingungen in Seitenkanalverdichtern,” Beiträge zu Fluidenergiemaschinen Band 5, Verlag und Bildarchiv W. H. Faragallah, 2000.
- M. J. Lighthill, “On Sound Generated Aerodynamically. Part I: General Theory,” Proceedings of the Royal Society London A, Vol. 211, No. 1107, 1952, pp. 564-587. http://dx.doi.org/10.1098/rspa.1952.0060
- M. J. Lighthill, “On Sound Generated Aerodynamically. Part II: Turbulence as a Source of Sound,” Proceedings of the Royal Society London, Vol. 264, 1954, pp. 321-342.

