American Journal of Computational Mathematics
Vol. 3 No. 2 (2013) , Article ID: 33551 , 6 pages DOI:10.4236/ajcm.2013.32025
Four Steps Continuous Method for the Solution of 
1Department of Mathematics, Modibbo Adama University of Technology, Yola, Nigeria
2Department of Mathematics and Statistics, Cross River State University of Technology, Calabar, Nigeria
Email: torlar10@yahoo.com, remi_odekunle@yahoo.com, *mfudo4sure@yahoo.com
Copyright © 2013 Adetola Olaide Adesanya et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 5, 2013; revised February 18, 2013; accepted March 30, 2013
Keywords: Predictor; Corrector; Collocation; Interpolation; Power Series Approximant; Continuous Block Method
ABSTRACT
This paper proposes a continuous block method for the solution of second order ordinary differential equation. Collocation and interpolation of the power series approximate solution are adopted to derive a continuous implicit linear multistep method. Continuous block method is used to derive the independent solution which is evaluated at selected grid points to generate the discrete block method. The order, consistency, zero stability and stability region are investigated. The new method was found to compare favourably with the existing methods in term of accuracy.
1. Introduction
This paper considered the solution to the second order initial value problem of the form
 (1)
(1)
Predictor-corrector method for solving higher order ordinary differential equation has been proposed by many scholars. These authors are [1-5]. They individually proposed continuous implicit linear multistep method where separate reducing order of accuracy predictors was developed and Taylor series expansion provided the starting value. The major setback of this method is the cost of developing predictors. Moreover, the predictors developed are of lower order to the corrector; hence it has a great effect on the accuracy of the results.
In order to cater for the shortcoming of predictor-corrector method, scholars proposed block method. Block method gives solutions at each grid within the interval of integration without ovelapping and the burden of developing separate predictors is eradicated. The authors who proposed block method are [6-12]. These authors proposed a discrete block method, which did not enable evaluation at all points within the interval of integration.
In this paper, we propose a continuous block method which enables evaluation at all points within the interval of integration without starting the block all over. Continuous block method enables one to recover discrete block when evaluating at selected grid points.
2. Methodology
Given the general block formulae proposed by [11]
 (2)
(2)
where 
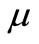 is the order of the differential equation,
is the order of the differential equation,  is the steplenght,
is the steplenght, 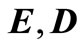 and
and 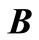 are matrices. We then propose a prediction equation in the form
are matrices. We then propose a prediction equation in the form
 (3)
(3)
where 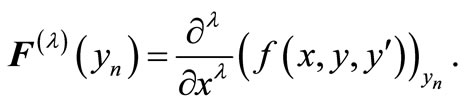 Substituting (3) into (2) gives
Substituting (3) into (2) gives
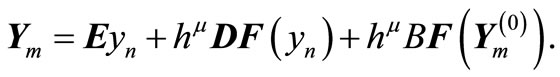 (4)
(4)
Equation (4) is non self starting since the prediction equation is not gotten directly from the block formulae as proposed by [13].
In formulating the continuous block method we now consider a continuous implicit linear multistep method given by
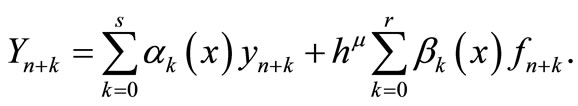 (5)
(5)
where  and
and  are the numbers of interpolation and collocation points.
are the numbers of interpolation and collocation points.  and
and 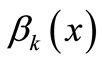 are polynomials.
are polynomials.
Solving (5) for the independent solution gives a continuous block formulae in the form
 (6)
(6)
where 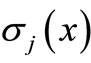 is a polynomial,
is a polynomial,  Evaluating (6) at selected value of
Evaluating (6) at selected value of 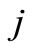 reduces to (2).
reduces to (2).
Development of the Continuous Block Formula
Consider power series of a single variable as our approximate solution in the form
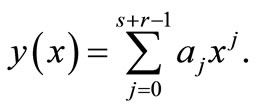 (7)
(7)
The second derivatives of (7) gives
 (8)
(8)
putting (8) into (1) gives
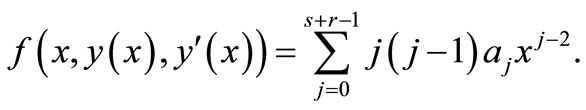 (9)
(9)
Let the solution to (1) be soughted on the partition  with a constant stepsize
with a constant stepsize 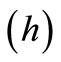 given as
given as

Interpolating (7) at 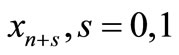 and collocating (9) at
and collocating (9) at  gives
gives
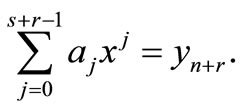 (10)
(10)
 (11)
(11)
solving (10) and (11) for  and substituting back in (7) gives a continuous linear multistep method of the form
and substituting back in (7) gives a continuous linear multistep method of the form
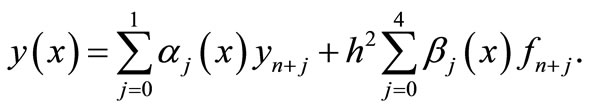 (12)
(12)
where the coefficient of 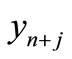 and
and  are given as
are given as
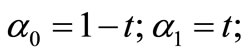
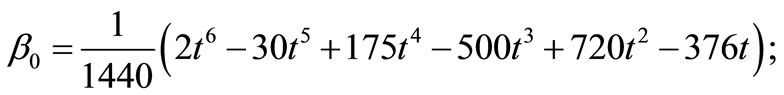



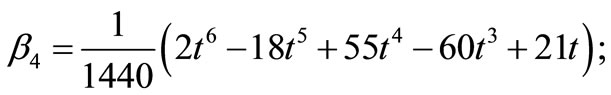
where
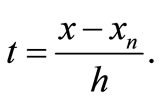
Solving for the independent solution  in (13) gives a continuous block formulae (12) where the coefficient of
in (13) gives a continuous block formulae (12) where the coefficient of  is given by
is given by



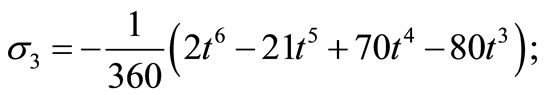
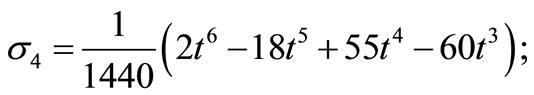
Evaluating the continuous block method at  gives a discrete block formulae of the form (2) where
gives a discrete block formulae of the form (2) where



 identity matrix.
identity matrix.
3. Analysis of the Basic Properties of the Corrector
3.1. Order of the Method
Let the linear operator 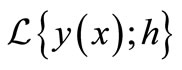 associated with the block formulae be defined as
associated with the block formulae be defined as
 (13)
(13)
expanding in Taylor series and comparing the coefficient of h gives
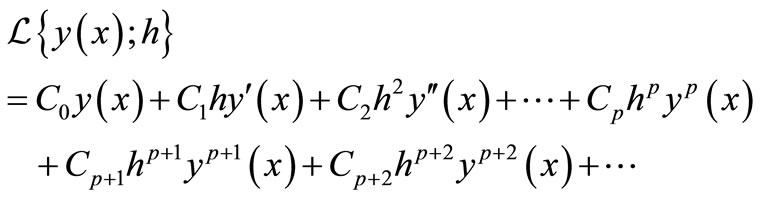 (14)
(14)
Definition 1. The linear operator  and the associated continuous linear multistep method (13) are said to be of order p if
and the associated continuous linear multistep method (13) are said to be of order p if 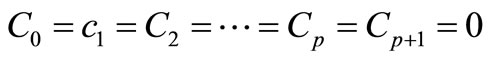 and
and 
 is called the error constant and implies that the local truncation error is given by
is called the error constant and implies that the local truncation error is given by
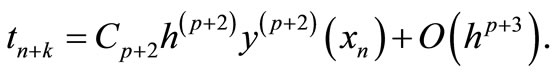 (15)
(15)
For our method,

Expanding in Taylor series gives
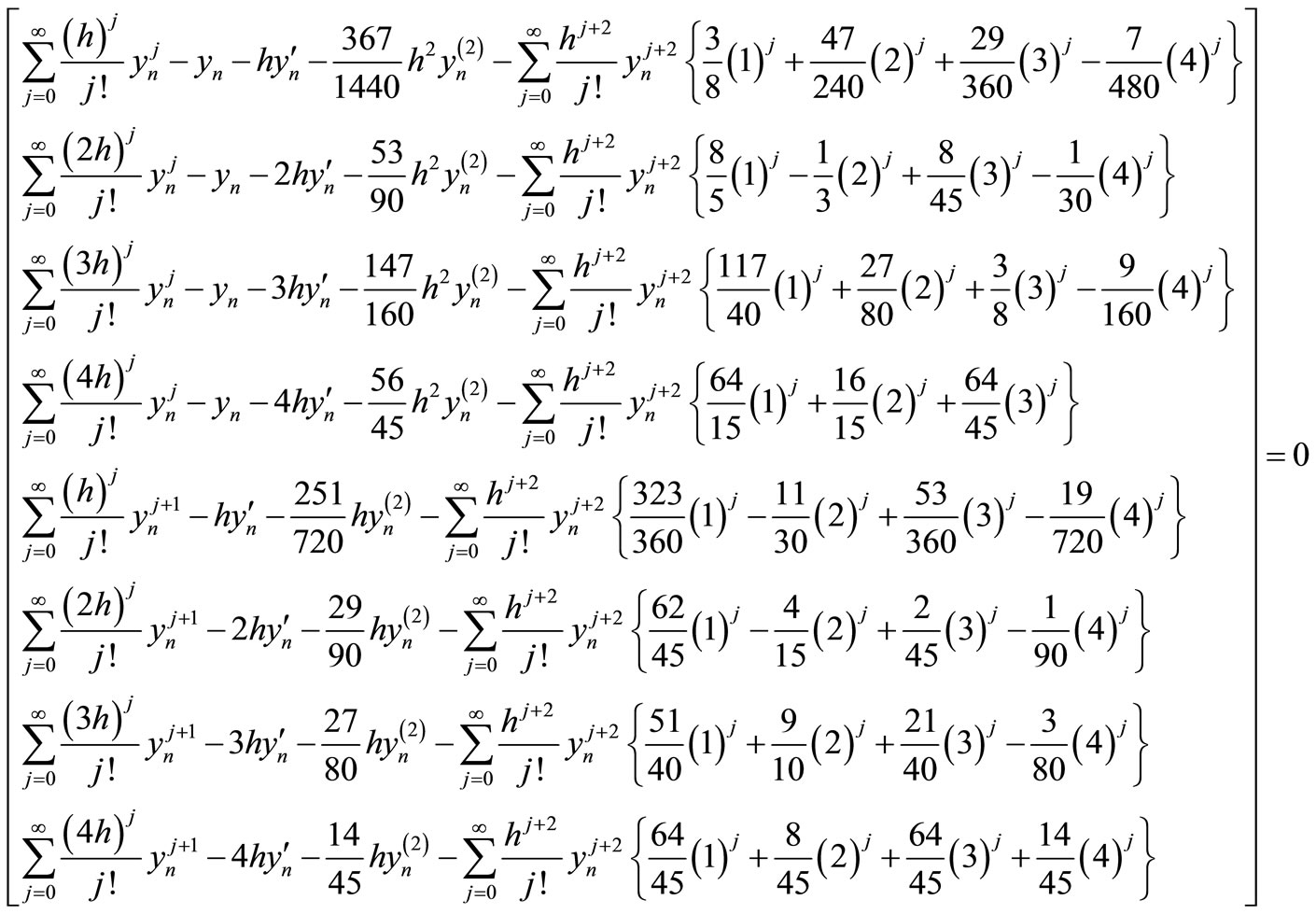
hence,
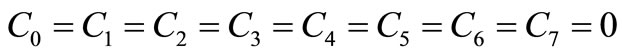

4. Zero Stability
Definition 2. The block (2) is said to be zero stable, if the roots 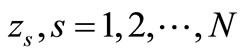 of the first characteristic polynomial
of the first characteristic polynomial  defined by
defined by  satisfies
satisfies 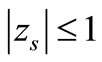 have multiplicity not exceeding the order of the differential equation. Moreover as
have multiplicity not exceeding the order of the differential equation. Moreover as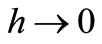 ,
,
 where
where 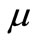 is the order of the differential equation, r is the order of the matrix
is the order of the differential equation, r is the order of the matrix 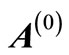 and E (see [11] for details).
and E (see [11] for details).
For our method

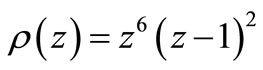 ; hence our method is zero stable.
; hence our method is zero stable.
Region of Absolute Stability
Definition 3. The method (2) is said be absolutely stable if for a given value oh h, all the roots  of the characteristic polynomial
of the characteristic polynomial 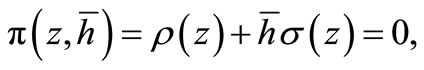 satisfies
satisfies  where
where  and
and .
.
We adopted the boundary locus method for the region of absolute stability if the block method. Substituting the test equation  into the block formula gives
into the block formula gives
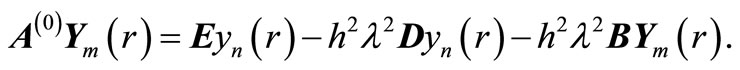

writing in trigonometric ratios gives
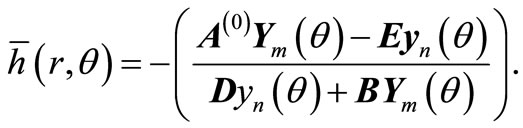 (16)
(16)
where 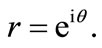 Equation (16) is our characteristics polynomial (see [14] for details). Applying to our method
Equation (16) is our characteristics polynomial (see [14] for details). Applying to our method

which gives the stability region to be [−14.35, 0] after evaluation  at interval of
at interval of  within [0, 180] The stability is shown in Figure 1.
within [0, 180] The stability is shown in Figure 1.
5. Numerical Experiments
5.1. Test Problems
We test our scheme on second order initial value problems.
Problem 1: Consider the non linear initial value problem (I.V.P) which was solved by [11] using block method and [2] for step size 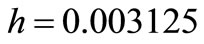 which is of order 8
which is of order 8
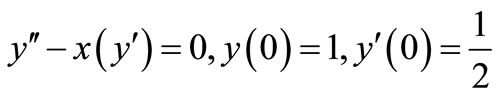
Exact solution: 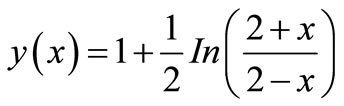
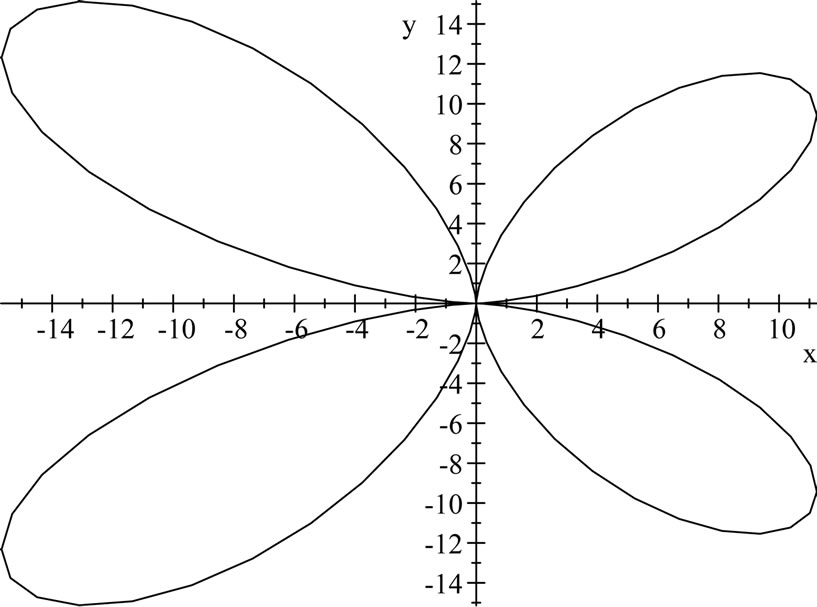
Figure 1. Showing region of absolute stability of the block method.
We solved this problem using our method for stepsize h = 0.01. The result is shown in Table 1. Our method performed better than the methods compared with. This problem method was also solved [10] using block of lower order for h = 1/32. Though the details are not shown but our result performed better in term of accuracy.
Problem 2: Consider a linear second order initial value problem
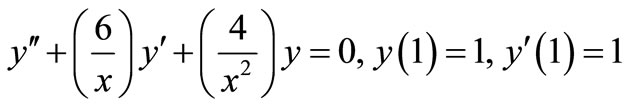
Exact solution: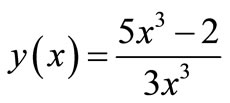 .
.
This problem was also solved by [10]. The result in
Table 2 shows clearly that our method gives better approximation than the existing methods.
5.2. Numerical Results
The following notations are used in the table ESBK: Error in [11];
EAK: Error in [2];
EBK: Error in [10];
 .
.
6. Conclusion
We have proposed a non self starting continuous block method in this paper. It has been shown clearly that the non self starting method gives a better approximation than
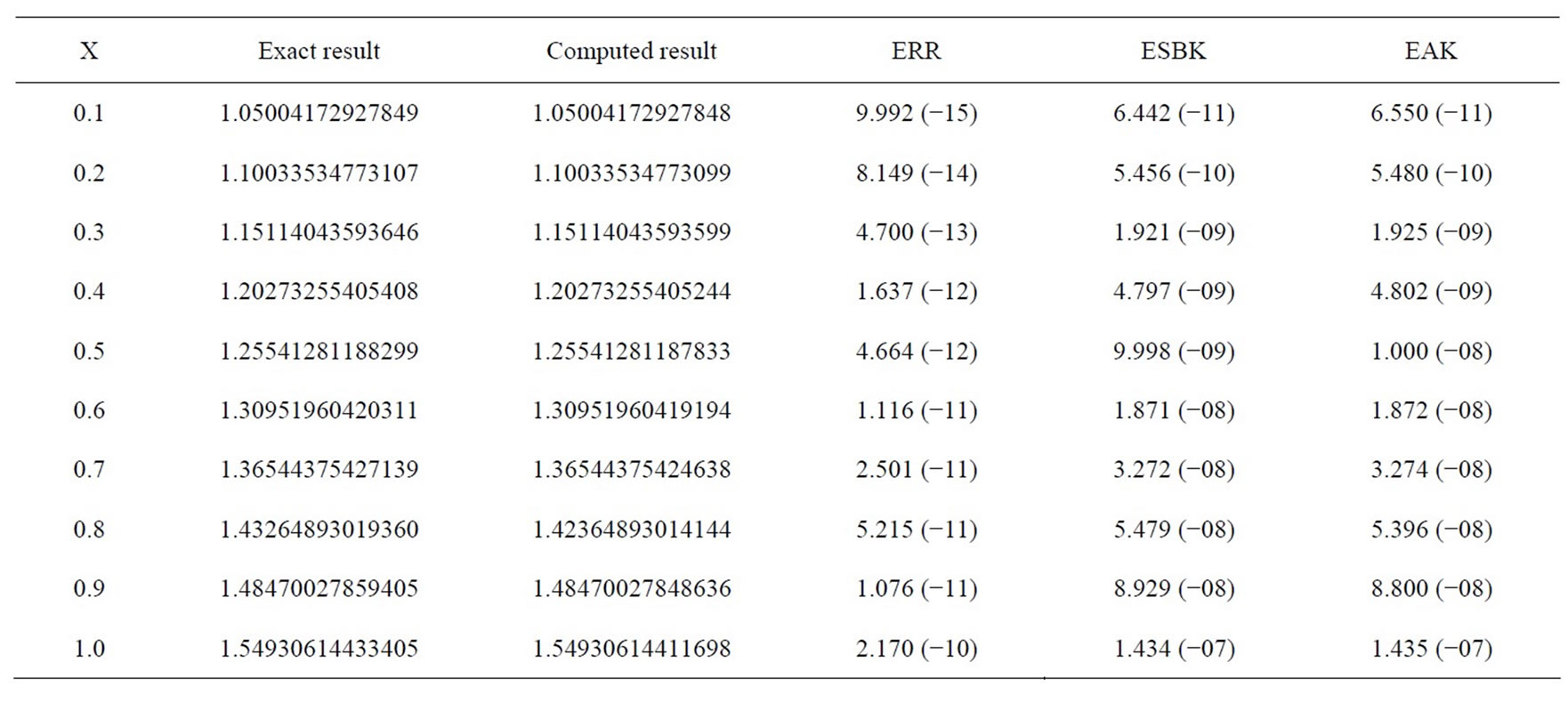
Table 1. Showing results of problem 1.

Table 2. Showing results of problem 2.
the self starting method. The continuous parameter introduced in the block method allows evaluation at all points within the interval of integration; hence, it enables researchers to understand the behaviour of the system under investigation. We therefore recommend this new method when seeking for the solution of initial value problems.
REFERENCES
- D. O. Awoyemi, “A New Sixth Order-Order Algorithm for the General Second Order Ordinary Differential Equation,” International Journal of Computer Mathematics, Vol. 77, No. 1, pp. 117-124. doi:10.1080/00207160108805054
- D. O. Awoyemi and S. J. Kayode, “A Maximal Order Collocation Method for Direct Solution of Initial Value Problems of General Second Order Ordinary Differential Equation,” Proceedings of the Conference Organised by the National Mathematical Centre, Abuja, 2005.
- S. O. Adee, P. Onumanyi, U. V. serisena and Y. A. Yahaya, “A Note on Starting Numerov’s Method More Accurately by an Hybrid Formula of Order Four for an Initial Value Problem,” Journal of Computational and Applied Mathematics, Vol. 175, No. 4, 2005, pp. 269-273.
- D. O. Awoyemi and M. O. Idowu, “A Class of Hybrid Collocation Method for Third Order Ordinary Differential Equation,” International Journal of Computer Mathematics, Vol. 82, No. 10, 2005, pp. 1287-1293. doi:10.1080/00207160500112902
- A. O. Adesanya, T. A. Anake and M. O. Udoh, “Improved Continuous Method for Direct Solution of General Second Order Ordinary Differential Equations,” Journal of Nigerian Association of Mathematical Physics, Vol. 13, 2008, pp. 59-62.
- S. N. Jator, “A Sixth Order Linear Multistep Method for Direct Solution of
 ,” International Journal of Pure and Applied Mathematics, Vol. 40, No. 1, 2007, pp. 457-472.
,” International Journal of Pure and Applied Mathematics, Vol. 40, No. 1, 2007, pp. 457-472. - S. N. Jator and J. Li, “A Self Starting Linear Multistep Method for the Direct Solution of the General Second Order Initial Value Problems,” International Journal of Computer Mathematics, Vol. 86, No. 5, 2009, pp. 817- 836. doi:10.1080/00207160701708250
- R. D’Ambrosio, M. Ferro and B. Paternoster, “Two-Steps Hybrid Method for
 ,” Journal of Applied Mathematics Letters, Vol. 22, No. 7, 2009, pp. 1076-1080. doi:10.1016/j.aml.2009.01.017
,” Journal of Applied Mathematics Letters, Vol. 22, No. 7, 2009, pp. 1076-1080. doi:10.1016/j.aml.2009.01.017 - I. Fudziah, H. K. Yap and O. Mohamad, “Explicit and Implicit 3-Point Block Method for Solving Special Second Order Ordinary Differential Equation Directly,” International Journal of Mathematical Analysis, Vol. 3, No. 5, 2009, pp. 239-254.
- Y. A. Yahaya and A. M. Badmus, “A Class of Collocation Methods for General Second Order Differential Equation,” African Journal of Math and Computer Research, Vol. 2, No. 4, 2009, pp. 69-71.
- D. O. Awoyemi, E. A. Adebile, A. O. Adesanya and T. A. Anake, “Modified Block Method for the Direct Solution of Second Order Ordinary Differential Equation,” International Journal of Applied Mathematics and Computation, Vol. 3, No. 3, 2011, pp. 181-188.
- S. Mehrkanoon, “A Direct Variable Step Block Multistep Method for Solving General Third Order ODEs,” Journal of Numerical Algorithms, Vol. 57, No. 1, 2011, pp. 53-66. doi:10.1007/s11075-010-9413-x
- S. Abbas, “Derivation of a new Block Method Similar to the Block Trapezoidal Rule for the Numerical Solution of First Order IVPs,” Science Echoes, Vol. 2, 2006, pp. 10- 24.
- A. O. Adesanya, “Block Method for Higher Order Ordinary Differential Equations,” Ph.D. Thesis, University of Technology, Akure, 2011, Unpublished.
NOTES
*Corresponding author.

