World Journal of Nuclear Science and Technology
Vol.2 No.4(2012), Article ID:23800,6 pages DOI:10.4236/wjnst.2012.24028
Reconstruction of the Neutron Flux in a Slab Reactor
Nuclear Engineering Department, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil
Email: *asilva@con.ufrj.br
Received September 4, 2012; revised October 6, 2012; accepted October 15, 2012
Keywords: Neutron Diffusion Equation; Neutron Flux; Slab Reactor
ABSTRACT
In this electronic article we use the one-dimensional multigroup neutron diffusion equation to reconstruct the neutron flux in a slab reactor from the nuclear parameters of the reactor, boundary and symmetry condition, initial flux and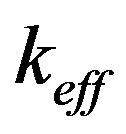 . The diffusion equation was solved analytically for one single homogeneous fuel region and for two regions considering fuel and reflector. To validate the method proposed, the results obtained in this article were compared using reference methods found in the literature.
. The diffusion equation was solved analytically for one single homogeneous fuel region and for two regions considering fuel and reflector. To validate the method proposed, the results obtained in this article were compared using reference methods found in the literature.
1. Introduction
In the analysis of the neutronic behaviour of a nuclear reactor, one of the most relevant parameters is the determining of the neutron flux in any region of the reactor core, as a precise assessment of this neutron flux will allow determining the spatial distribution of the reactor’s power, as well as other parameters of equal relevance for safe reactor operation such as reactor switching off margin and the value for the control rods [1].
Due to the need of precisely determining the neutron flux, some methods were created with this purpose, which take into consideration the geometry and composition of the reactor core. Amongst the many methods, we can point the calculation of the neutron flux from the multigroup diffusion equation through the finite difference method. This method is simple and of easy implementation, although it requires great computing effort for cases of practical interest, given that there is a need to use an extremely fine mesh.
With the aim of avoiding the large computing effort inherent to the finite difference method, several methods have come to the fore, called nodal methods, which allow the use of a coarse mesh (node); however, the use of these methods provides only average flux values for a given region. This way, one needs to use reconstruction methods [2,3] to obtain the neutron flux at any point of the reactor core.
There are many pin power reconstruction methods for few-group, some methods use polynomial expansions for representation of the intranodal flux distribution [3] and others new methods employs the analytical solution of Helmholtz equation satisfying a given set of boundary conditions. According [3] the analytical solution renders superior accuracy compared to polynomial based method.
Aimed at the need for new reconstruction methods that are fast and accurate [4,5], this work presents a method based on the analytical solution for the neutron flux from the solution of the neutron diffusion equation for two energy groups in one dimension, using boundary and symmetry conditions.
2. Multigroup Neutron Diffusion Equation
We have seen advances in recent decades in the development of coarse-mesh nodal methods aimed at numerically solving the one-dimensional multigroup neutron diffusion equation. These methods calculate with great precision the eigenvalue and neutron flux in each node as seen in the comparison with some reference methods (usually fine-mesh calculations). Amongst them, we point the nodal expansion method (NEM) [6-8] that uses the continuity equation and Fick’s Law [9]. The neutron continuity equation and Fick’s Law in one dimension, two groups of energy and stationary state are expressed by the following equations, respectively:
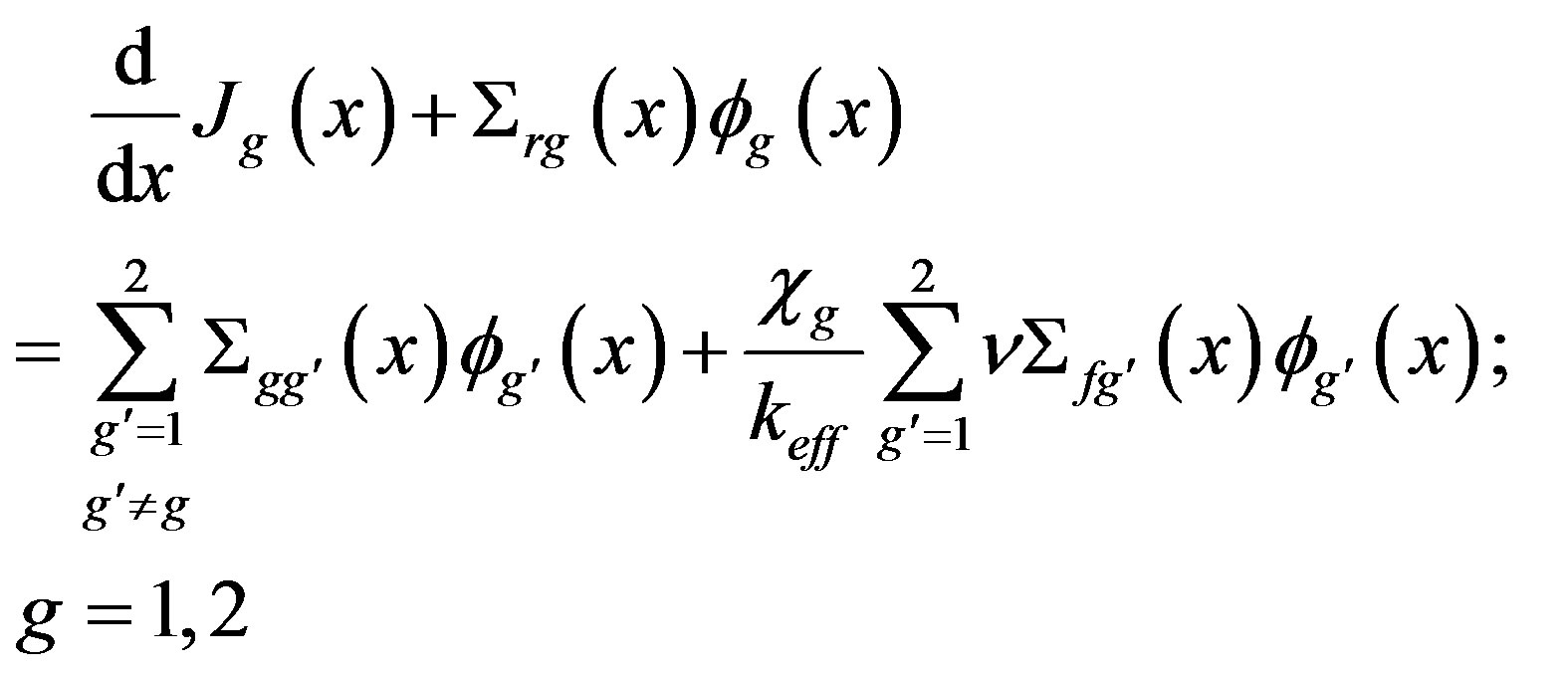 (1)
(1)
and
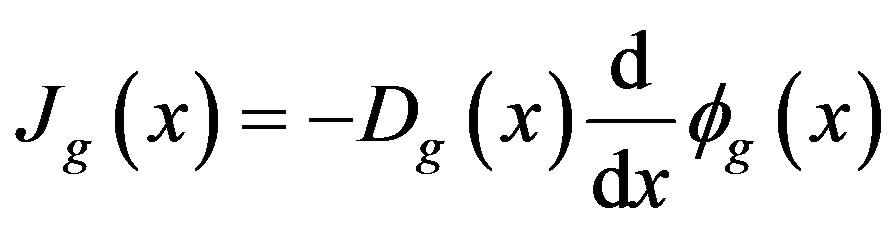 (2)
(2)
By replacing Equation (2) in Equation (1) we have the neutron diffusion equation [1] expressed in terms of the neutron flux, such that,
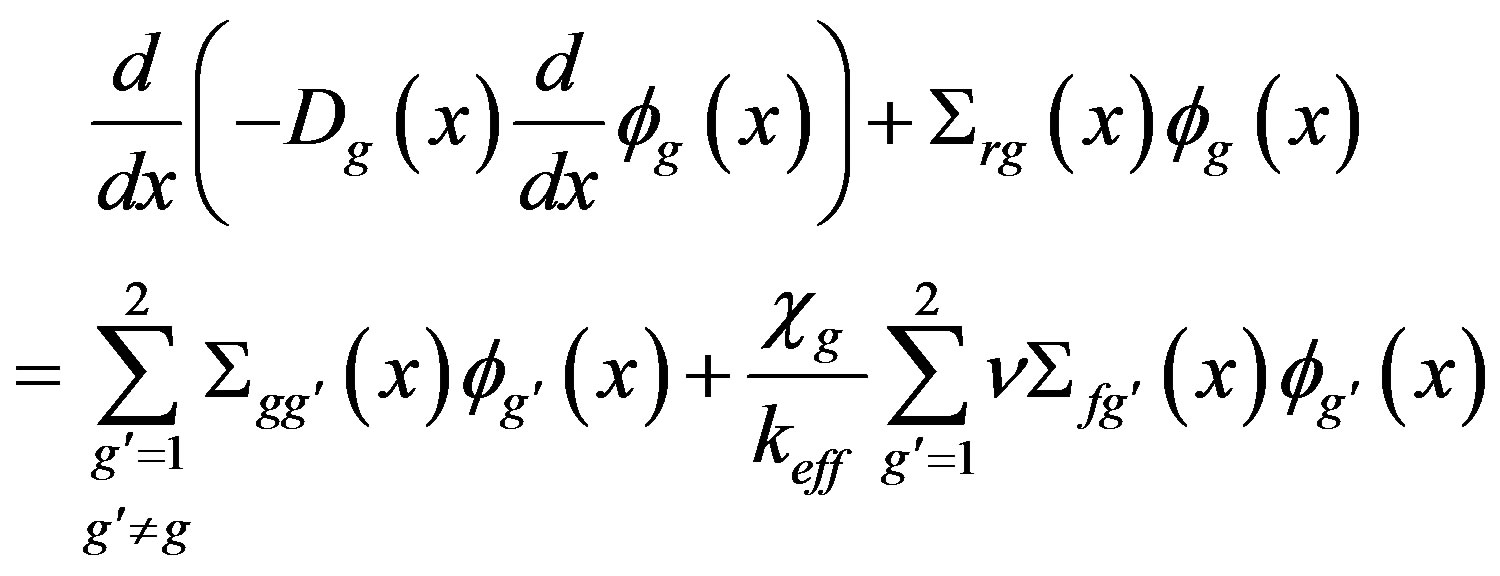 (3)
(3)
where  is the diffusion coefficient for group g,
is the diffusion coefficient for group g, 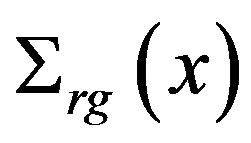 is the macroscopic removal cross section,
is the macroscopic removal cross section, 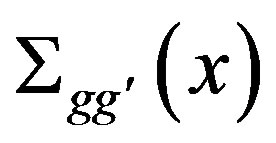 is the macroscopic scattering cross section from group g' to group g,
is the macroscopic scattering cross section from group g' to group g, 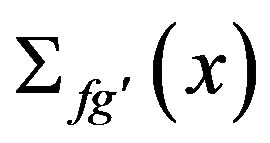 is the product of the average number of neutrons emitted by fission by the macroscopic fission cross section,
is the product of the average number of neutrons emitted by fission by the macroscopic fission cross section, 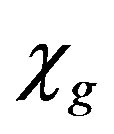 is the fission spectrum,
is the fission spectrum, 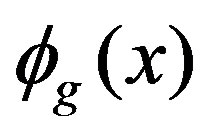 is the neutron flux and
is the neutron flux and  is the eigenvalue of the problem.
is the eigenvalue of the problem.
Due to the fact of the reactor to be homogeneous in the case of one single region (fuel) or homogeneous per part in the case of more than one region (fuel and reflector), these nuclear parameters are constant in each region, i.e.:
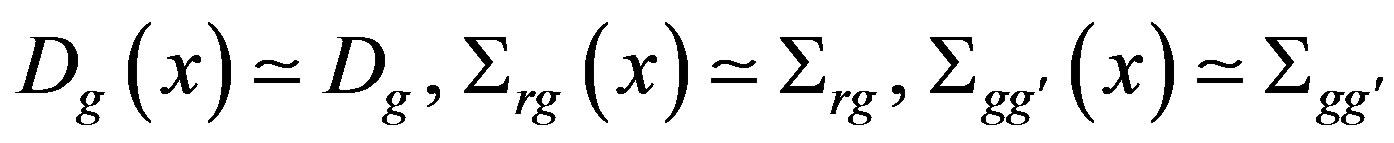
and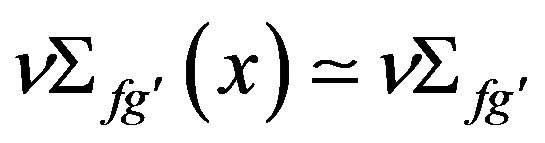 . With this, Equation (3) it becomes:
. With this, Equation (3) it becomes:
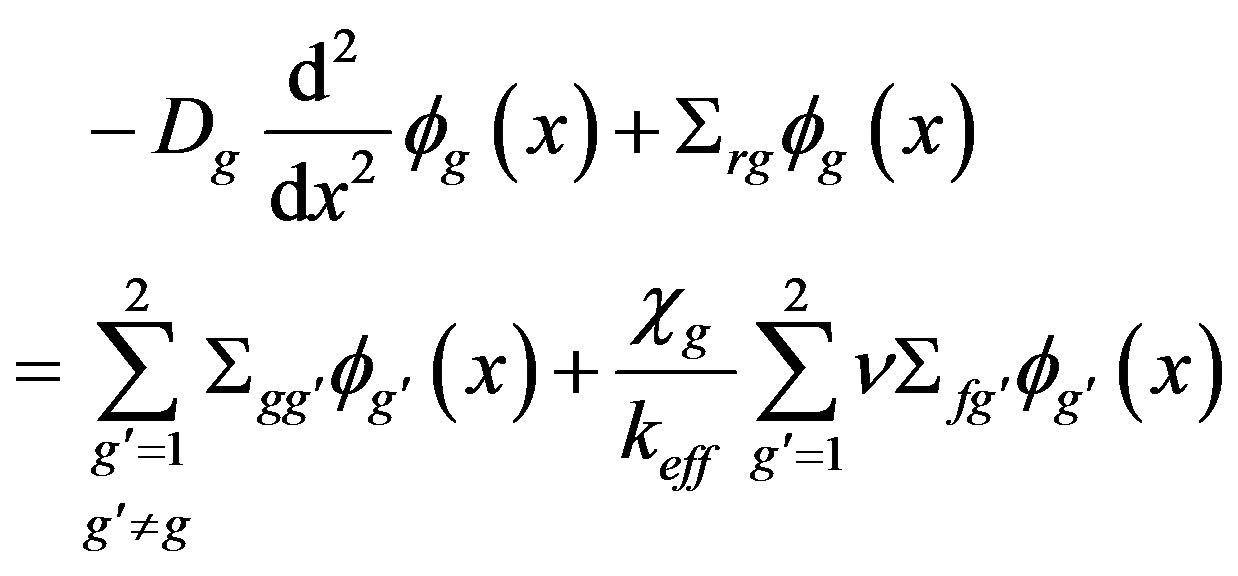 (4)
(4)
We shall seek an analytical solution from Equation (4) for the following cases: Homogeneous slab reactor consisting only of fuel and a heterogeneous slab reactor consisting of fuel and reflector as we shall describe in the next sections.
3. Analytical Solution for the Neutron Diffusion Equation for a Homogeneous Slab Reactor
The multigroup neutron diffusion equation defined as a eigenvalue problem can be written in the matrix form as follows:
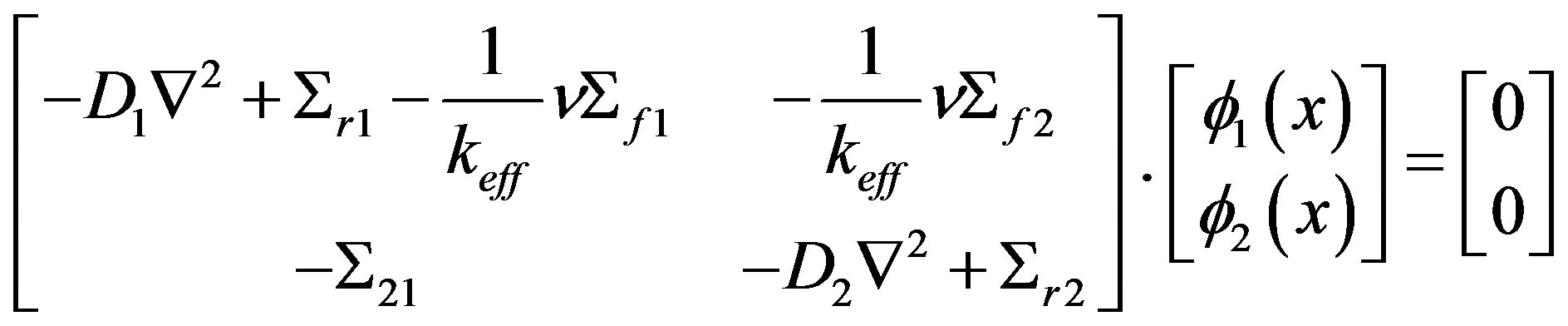 (5)
(5)
where 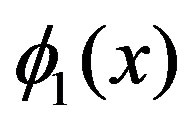 and
and  represent respectively the fast and thermal neutron flux. If we study the equation above it is possible to see that the equations both for the fast flux and for the thermal flux satisfy Helmholtz’s equation, given by:
represent respectively the fast and thermal neutron flux. If we study the equation above it is possible to see that the equations both for the fast flux and for the thermal flux satisfy Helmholtz’s equation, given by:
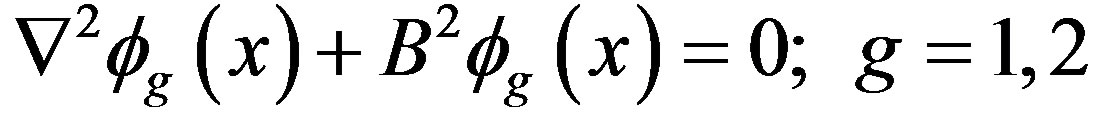 (6)
(6)
where 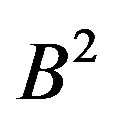 denotes any one of the two roots of the equation characteristic of the second-order equation in
denotes any one of the two roots of the equation characteristic of the second-order equation in . By replacing Equation (6) in Equation (5), it results that:
. By replacing Equation (6) in Equation (5), it results that:
 (7)
(7)
For Equation (7) to be solved, it is enough that the determinant of the matrix is null, i.e.,
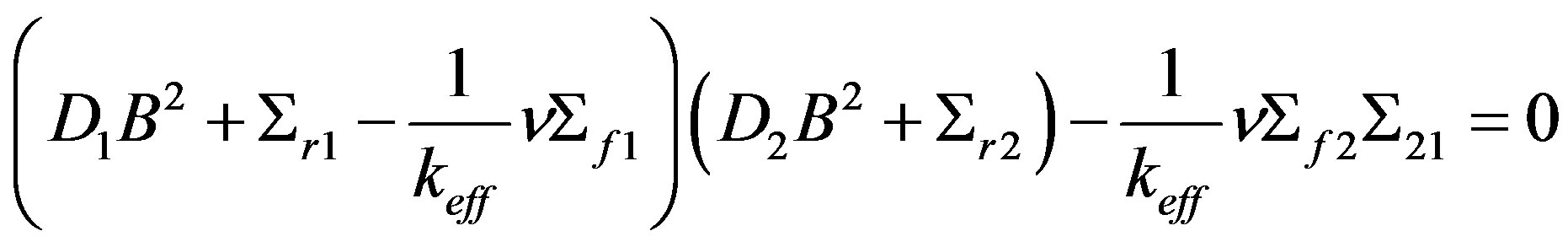
from which it produces
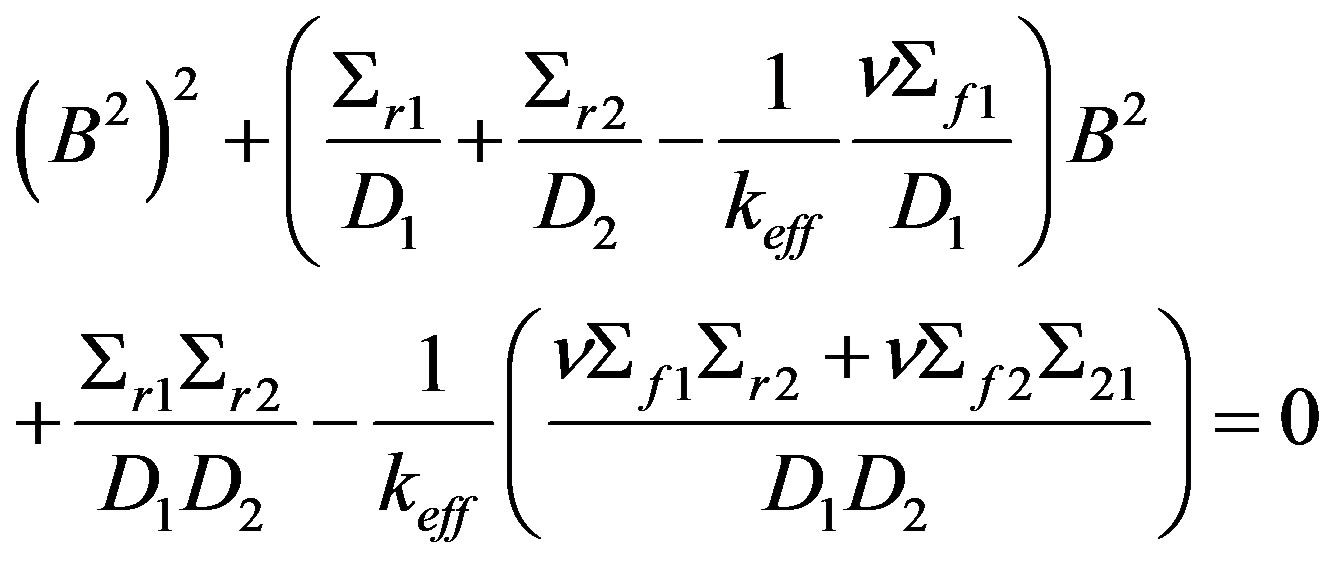 (8)
(8)
Note that we have a second-degree equation for 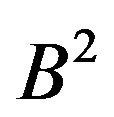 whose solution is given by:
whose solution is given by:
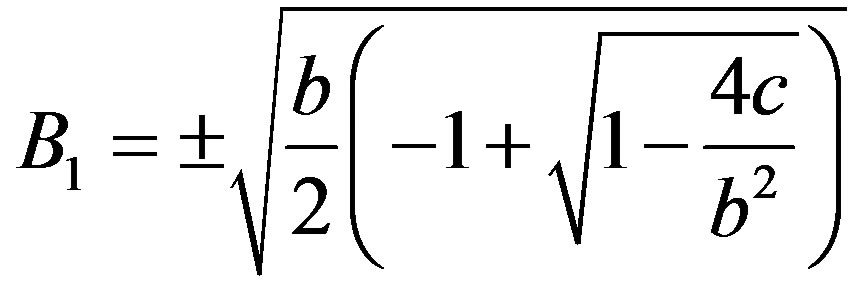
and
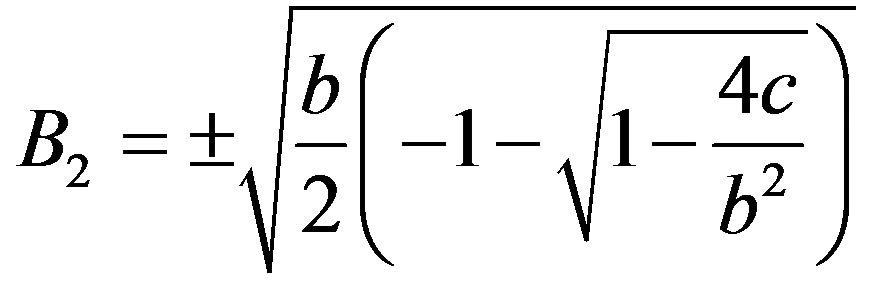
with
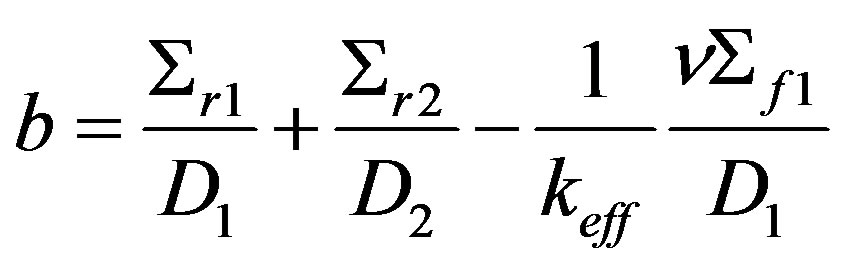
and
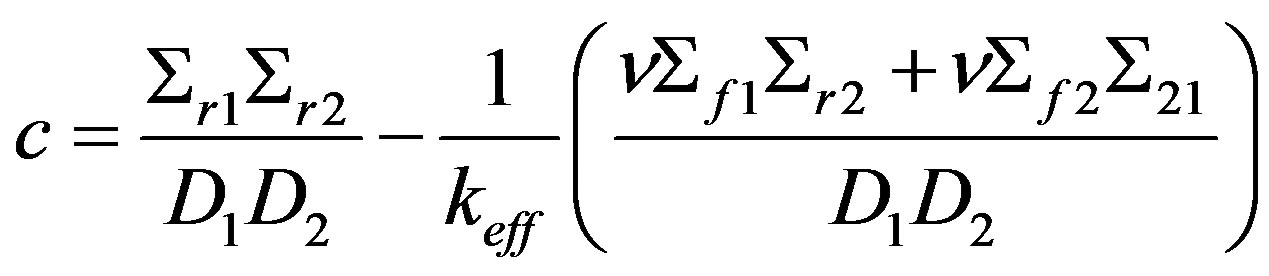 .
.
Note that until now we only seek to find the roots of the characteristic equation. As we have not defined the type of solution and we know that the diffusion equation is a second-order differential equation, the types of solution that satisfy this equation are many, although we will consider that this solution has an exponential behaviour for both fast and thermal flux. Thus, the general solution for the thermal flux is given by:
 (9)
(9)
Due to the fact that the system provided by Equation (5) is coupled, the solution for the fast flux can be obtained by replacing Equation (9) in (4) to , of which we have,
, of which we have,
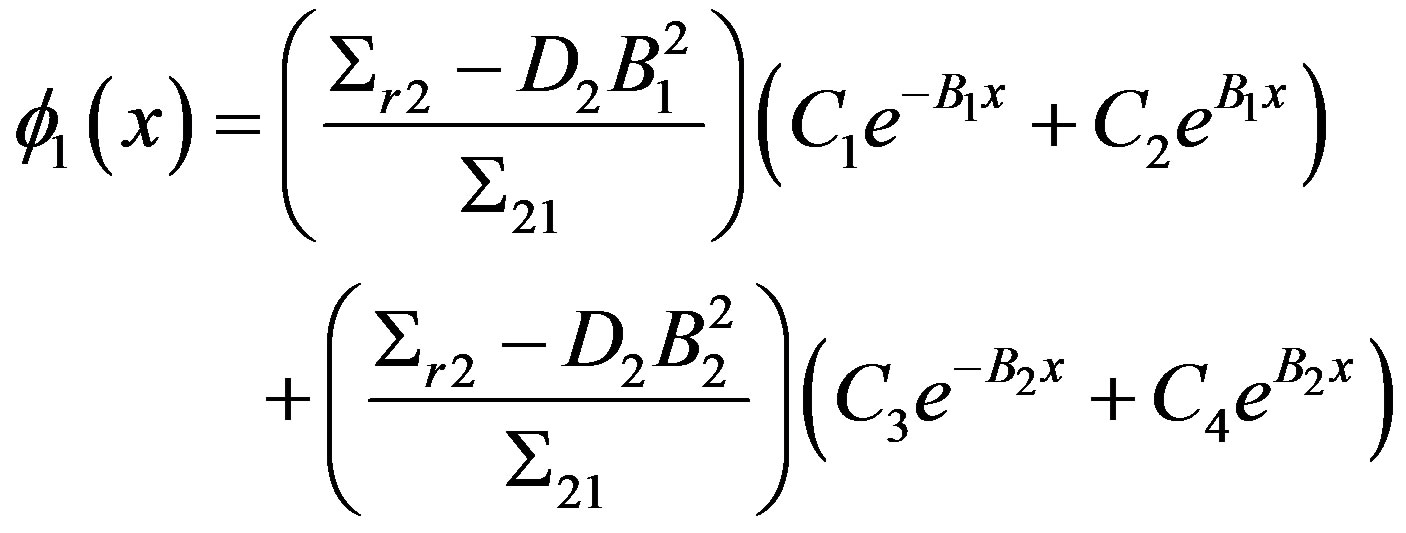 (10)
(10)
We will now seek some conditions that have to be applied to Equation (9) or (10) in order to determine the coefficients of the equation. Note that the coefficients are the same for the fast and thermal flow, so one only needs to impose contour and symmetry conditions for only one of the equations. In the case of a slab reactor [9] (plain slab in direction x) of dimension a as shown in Figure 1, we can impose the following conditions:
1) Null flux in the boundary the left, such that,
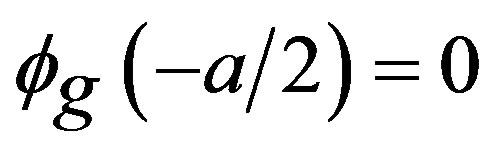 ;
;
2) Null flux in the boundary the right, such that,
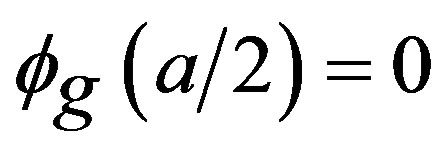 ;
;
3) Maximum flux in the origin, i.e.,
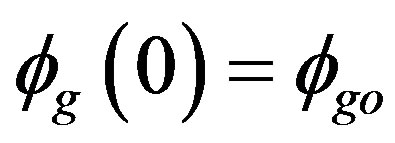 ;
;
4) Null net current in the origin,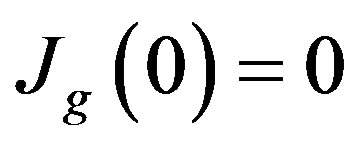 .
.
From these conditions, we can build a system with four conditions and four unknowns such as, for example, for the thermal group the neutron flux coefficients can be determined, such that,
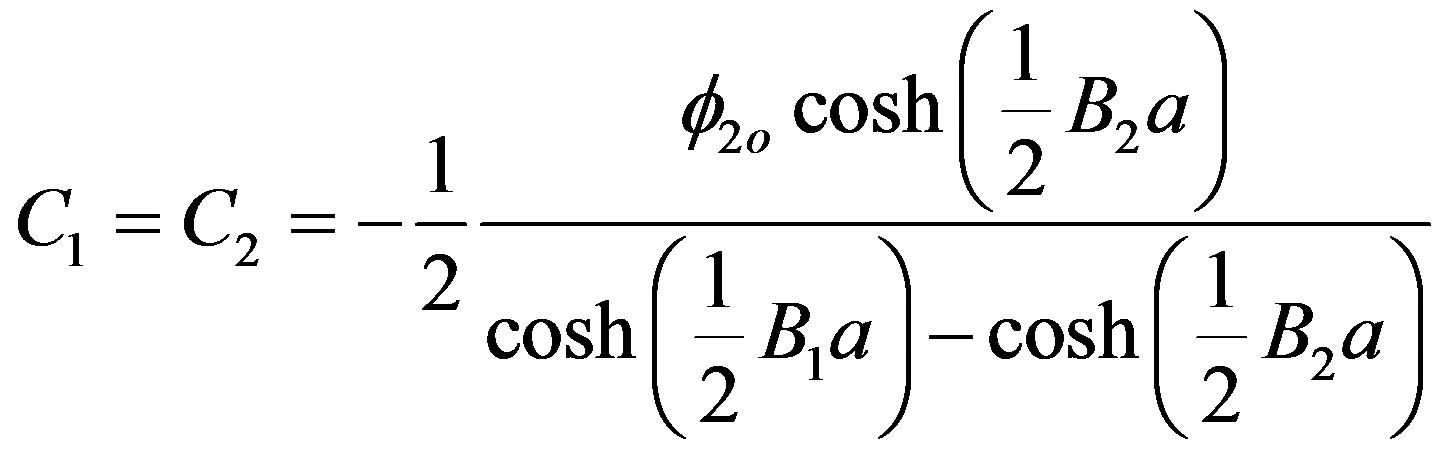 (11)
(11)
and
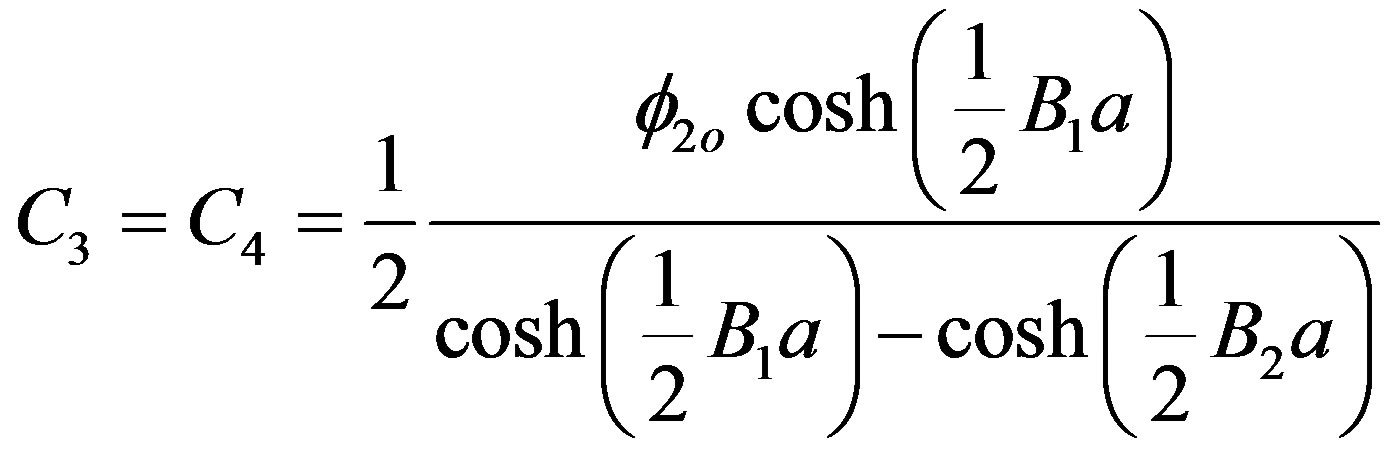 (12)
(12)
We will now analyze the case where the roots for B1 or B2 have negative values. We will first verify if
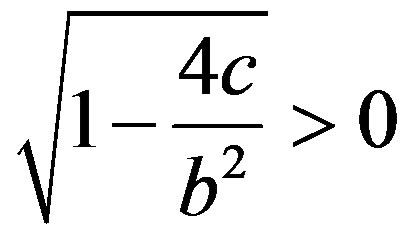
For that, it is enough to analyze if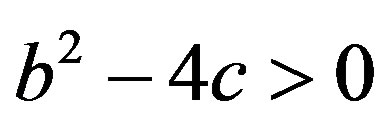 , i.e.:
, i.e.:
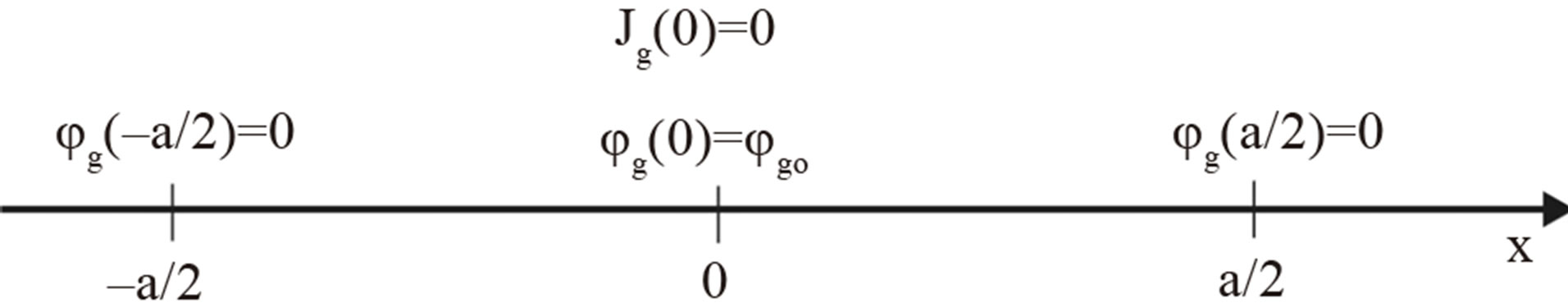
Figure 1. Slab reactor with an a dimension.
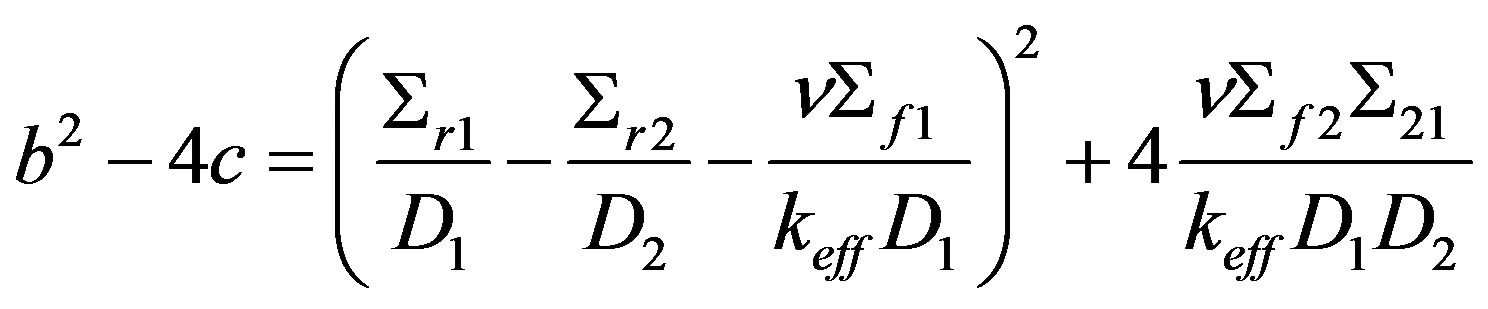
As we could see in the previous equation, the first term is always positive, as it is squared whereas the second term, as it only depends of nuclear parameters and of the eigenvalue, thus it is also positive. With this, we ensure that possible values for B1 and B2 are actual positive or negative values.
In a more general way we can simplify these notations using hyperbolic or trigonometric functions with the possible values for Bn, with n = 1, 2, such that the neutron flux is:
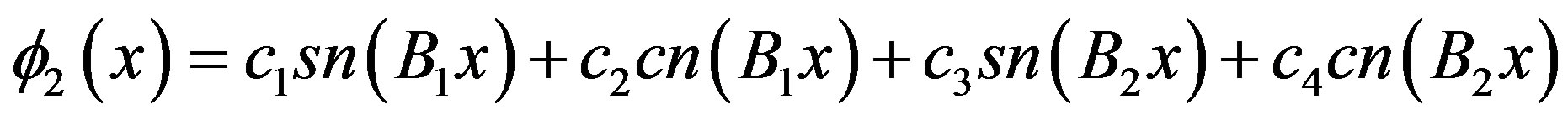 (13)
(13)
and
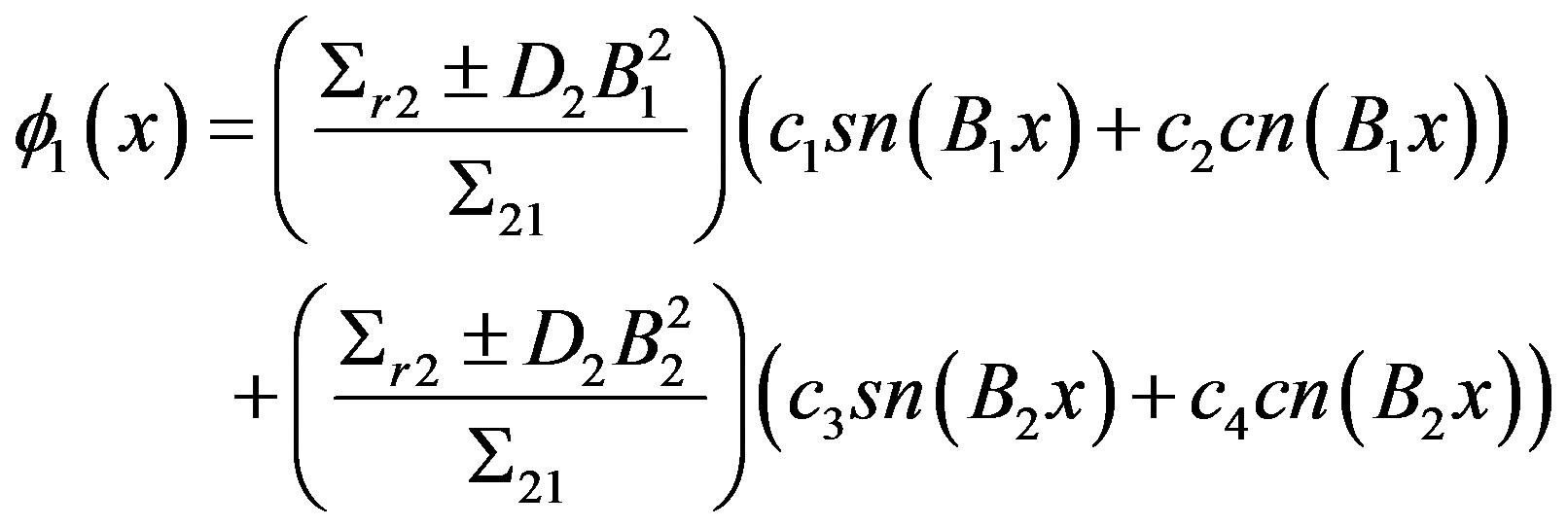 (14)
(14)
where these functions are given by:
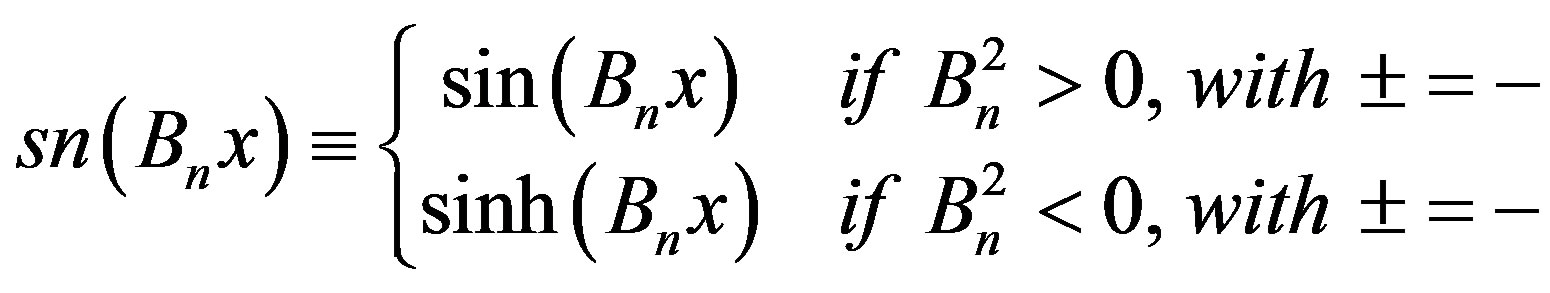
and
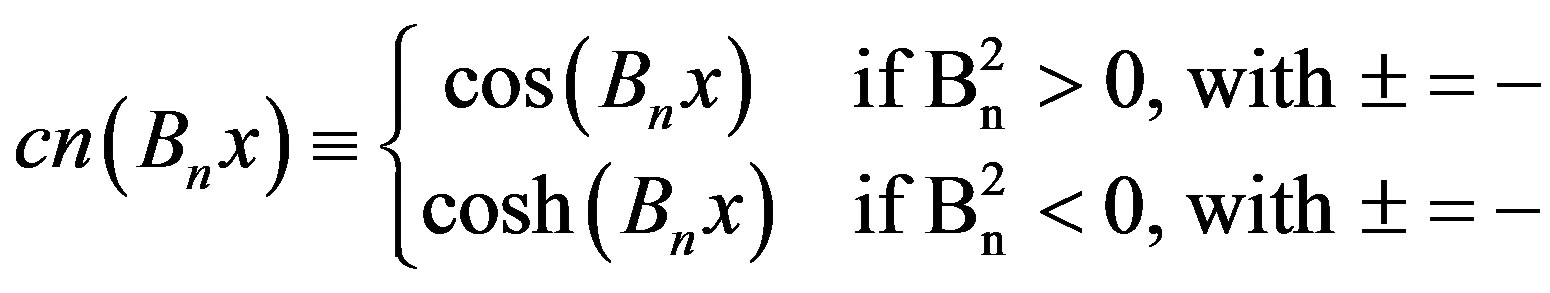
Note that for each case mentioned above, the equations for the fast and thermal flux will be different, that is, they may be expressed in terms of hyperbolic or trigonometric functions, or combinations of hyperbolic or trigonometric functions. This will depend of the nuclear parameters used in the calculations and of the eigenvalue. It is worth remembering that the coefficients depend of the values for the roots of Bn. However, the conditions of the problem do not change, i.e., a null flux in the boundary, null net current in the symmetry axis and constant initial flux.
4. Analytical Solution of the Neutron Diffusion Equation for a Heterogeneous Slab Reactor
The one-dimensional multigroup neutron diffusion equation for the fuel region was presented in the previous section, whose solution was given by Equations (9) and (10). For the reflector region this equation undergoes some modifications both in the nuclear parameters that will be different in relation to the nuclear parameters for the fuel, as well as for the form of the diffusion equation, given that for this region there is no neutron fission. Therefore, this equation can be written as follows:
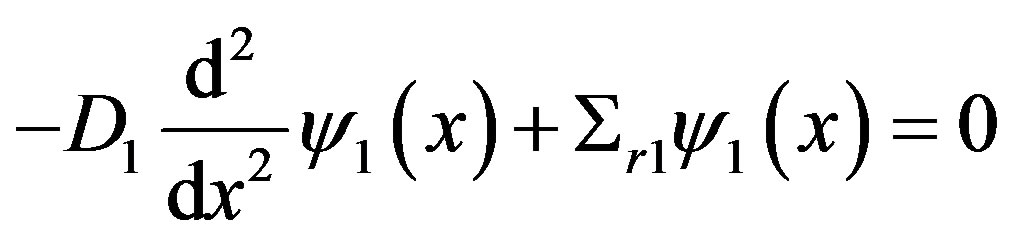 (15)
(15)
and
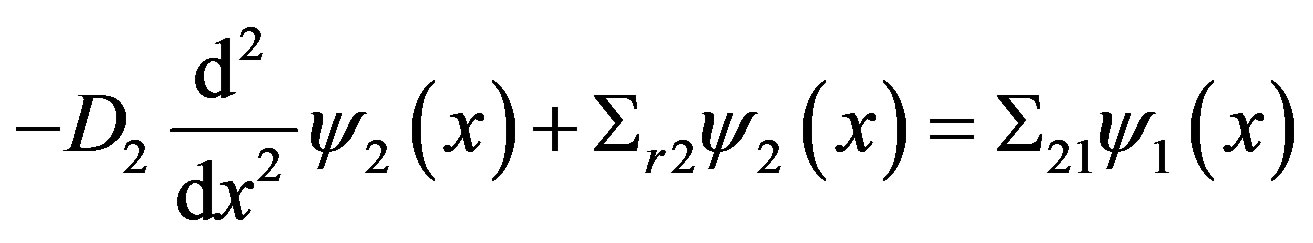 (16)
(16)
The solutions of the diffusion equation for the fast and thermal group for the reflector region are, respectively,
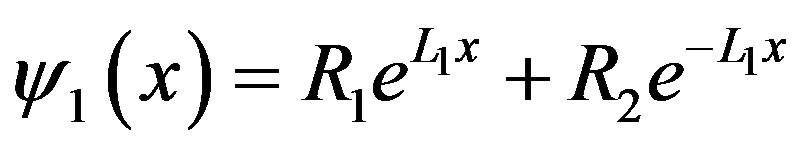 (17)
(17)
and
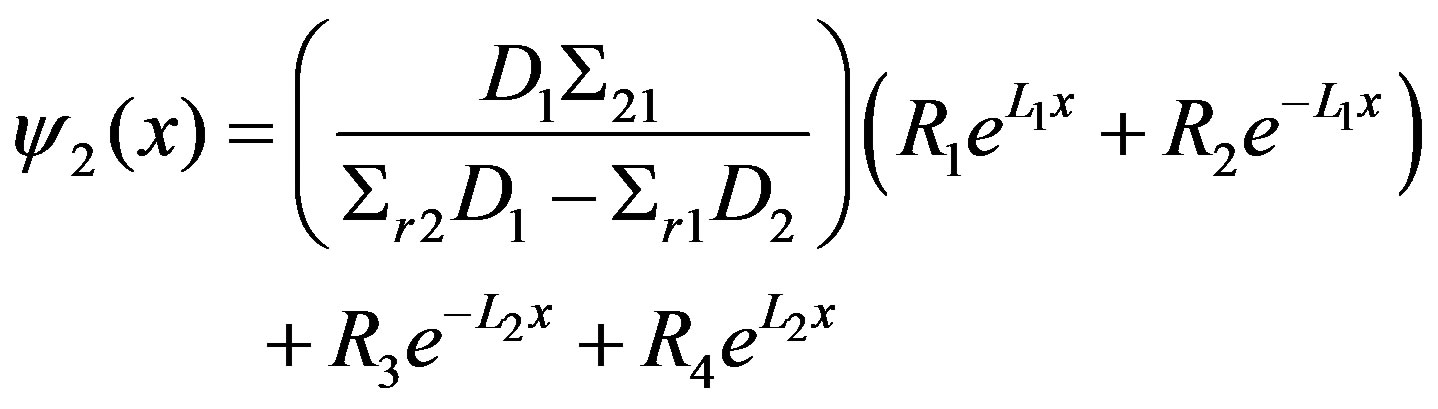 (18)
(18)
where 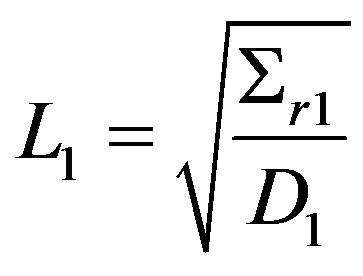 and
and 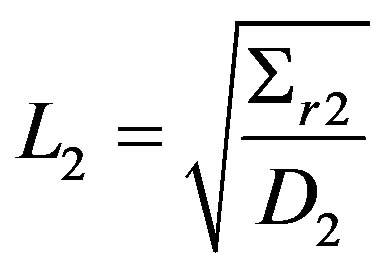 are the respective diffusion lengths for the fast and thermal groups.
are the respective diffusion lengths for the fast and thermal groups.
Equations (17) and (18) represent the solutions for the neutron flux in the reflector region, while Equations (9) and (10) represent the solutions for the neutron flux in the fuel region. These regions are shown in Figure 2.
As we already have the solutions for the flux in the two regions of the reactor, we will now seek to find which condition we should impose to the flux in order to determine the coefficients for Equations (9), (10), (17) and (18). As the coefficients for Equation (17) are present in Equation (18) and the coefficients for Equations (9) and (10) are identical, we will apply the conditions only for thermal flux in the two regions, fuel and reflector, such that
1) Continuity of flux in the interface between regions to the left, such that,
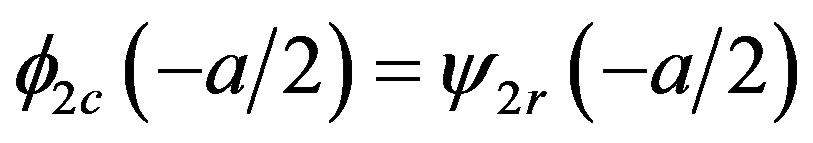 ;
;
2) Continuity of flux in the interface between regions to the right, such that,
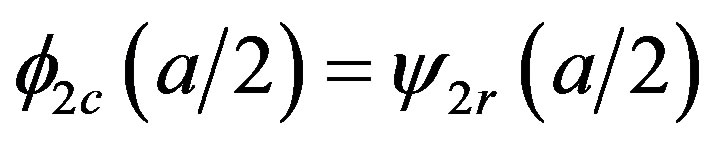 ;
;
3) Continuity of current in the interface between regions to the left, such that,
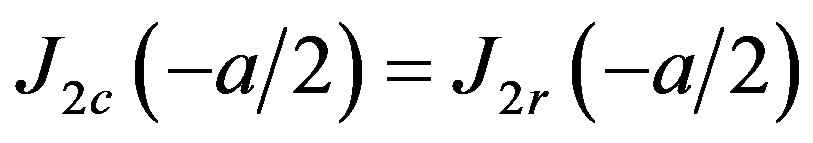 ;
;
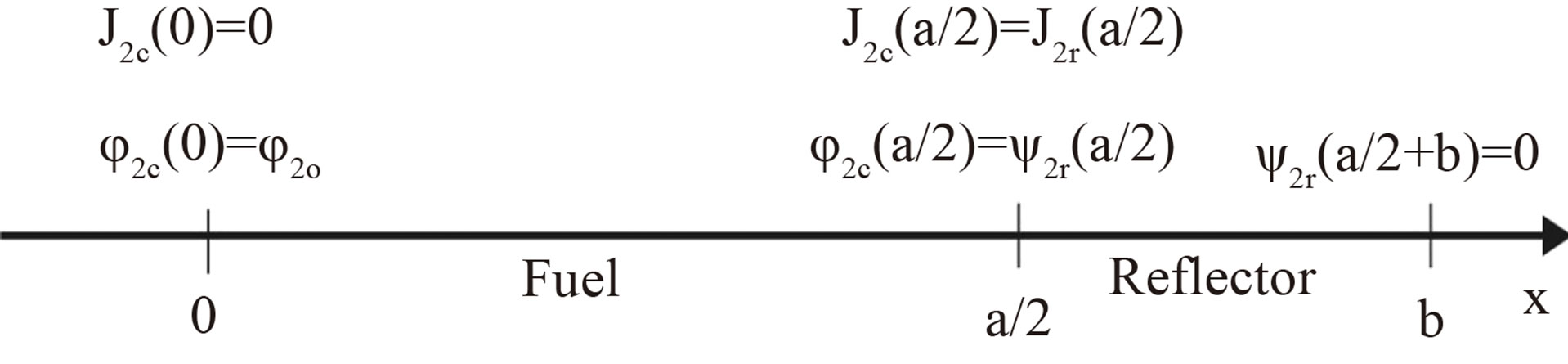
Figure 2. Slab reactor with two regions of dimension a + 2b.
4) Continuity of current in the interface between regions to the right, such that,
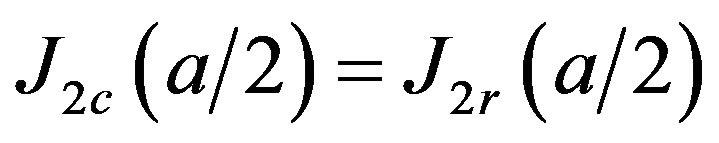 ;
;
5) Null flux in the contour to the left, such that,
 ;
;
6) Null flux in the contour to the right, such that,
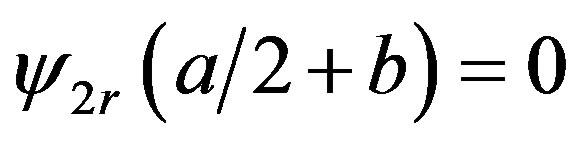 ;
;
7) Maximum flux in the origin, i.e.,
 ;
;
8) Null net current in the origin
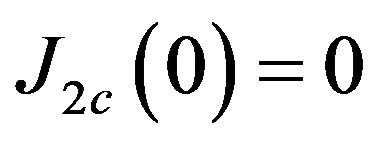 .
.
Subscripts c and r represent respectively, the fuel and reflector regions.
Note that, due to the fact that the equations have eight coefficients to be determined, it became necessary to impose eight conditions in order to determine these coefficients as mentioned earlier.
5. Results
This section presents the results obtained in the analytical solution of the neutron diffusion equation and compares the results obtained with the nodal expansion method (NEM) [1] and with the finite differences method (FDM) [10]. Table 1 shows the nuclear parameters used in the calculation of a homogeneous slab reactor of a = 100 cm dimension and eigenvalue 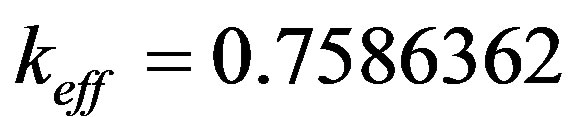 obtained by the finite difference method.
obtained by the finite difference method.
Figures 3 and 4 show the results obtained for fast and thermal flux, respectively, comparing the analytical solution (Analytic) with the nodal expansion method (NEM) and finite difference method (FDM).
We can see that the results are quite satisfactory for both fast and thermal fluxes. The only input data used in the analytical solution from the numerical results was: eigenvalue 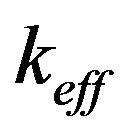 and initial flux
and initial flux . With this data we were able to reconstruct the entire neutron flux point-bypoint in the homogeneous reactor.
. With this data we were able to reconstruct the entire neutron flux point-bypoint in the homogeneous reactor.
We will now present the results obtained by the analytical solution for a slab reactor with two distinct regions, i.e., fuel and reflector. The nuclear parameters used in this calculation are shown in Table 2.
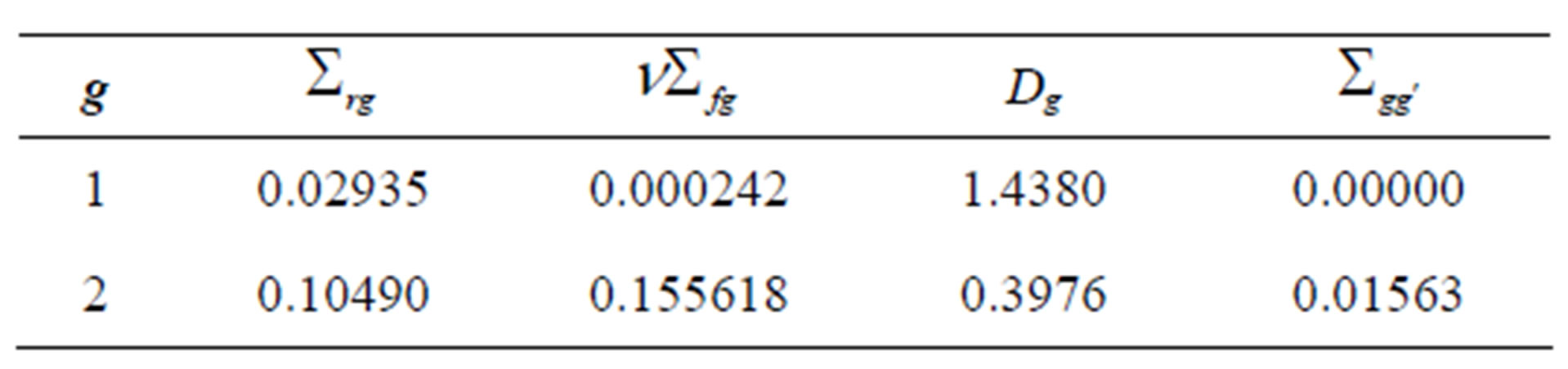
Table 1. Nuclear parameters for a homogeneous slab reactor.
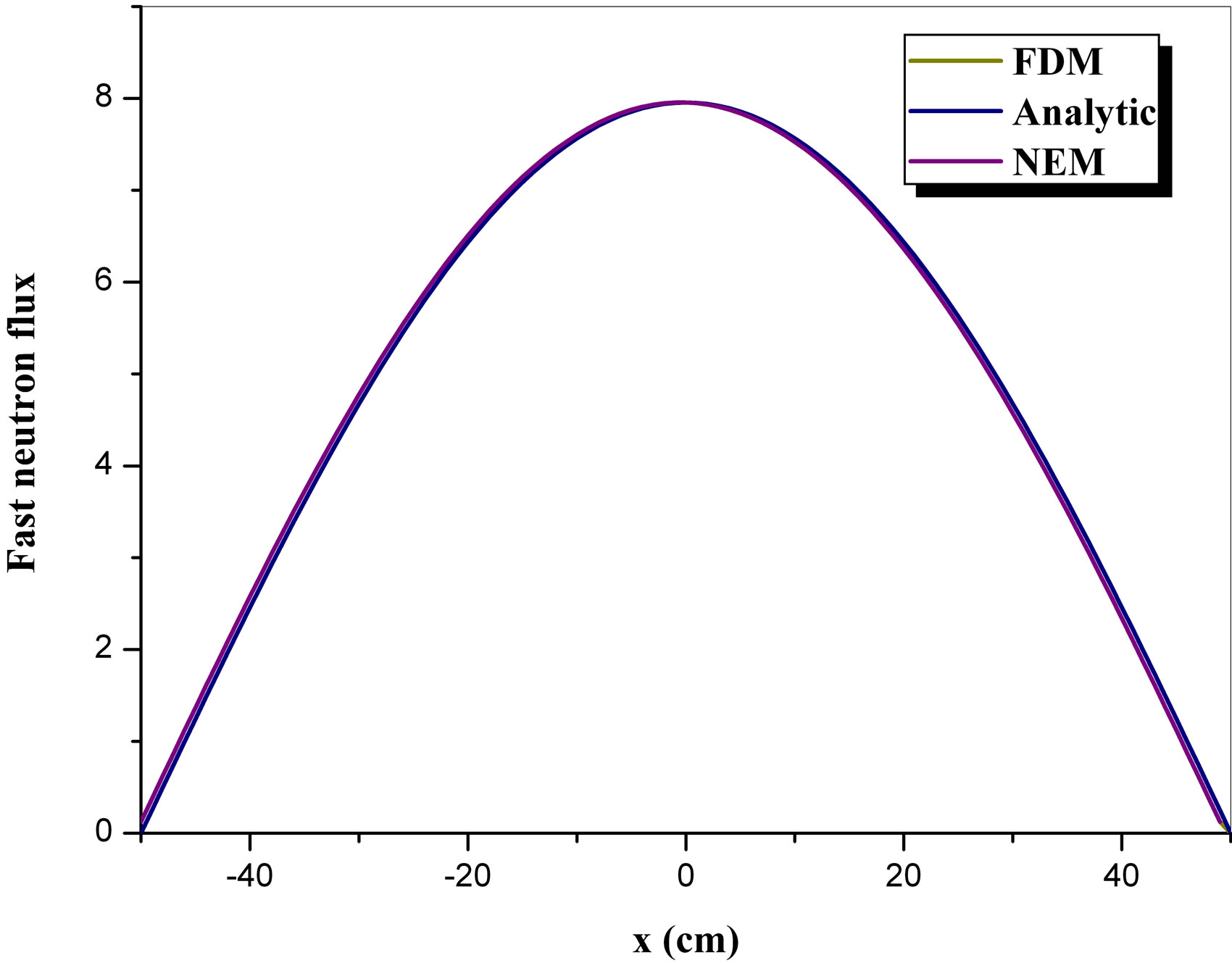
Figure 3. Comparison of fast neutron flux.
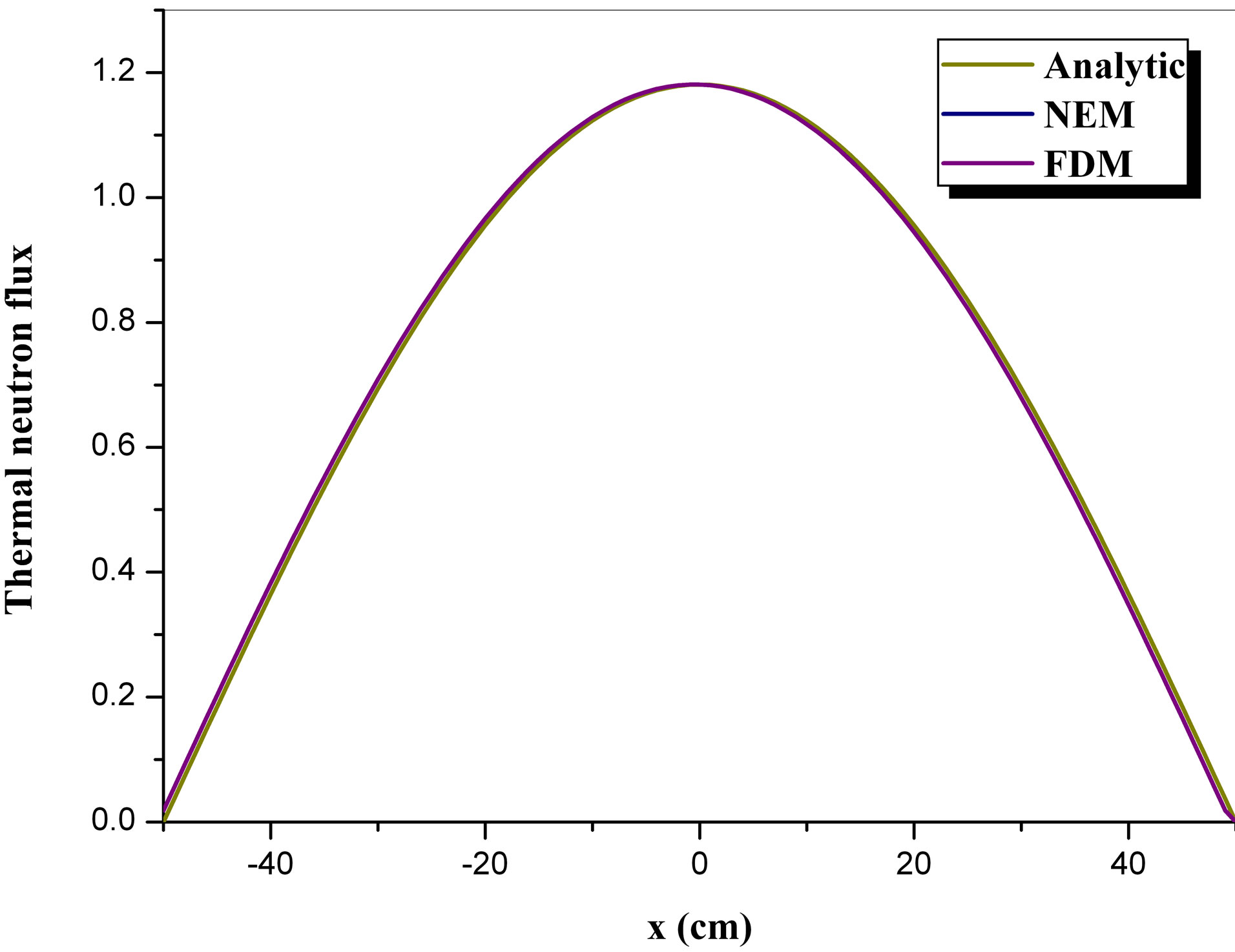
Figure 4. Comparison of thermal neutron flux.
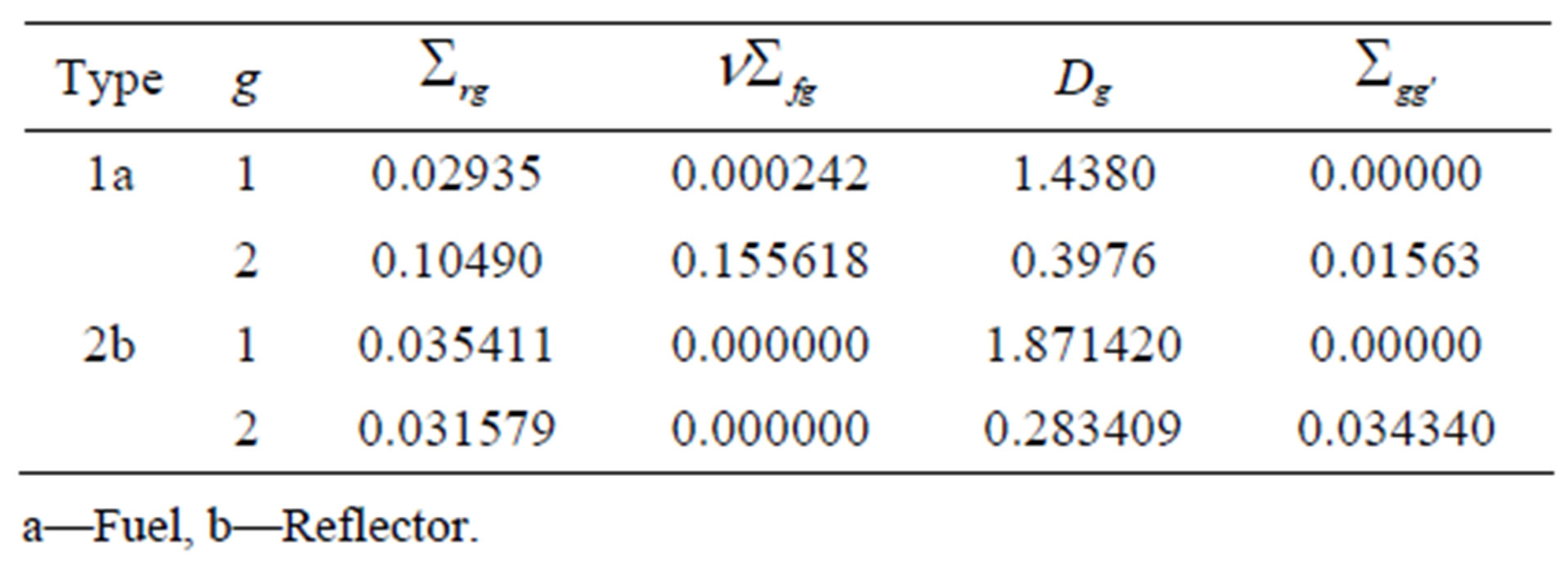
Table 2. Nuclear parameters for heterogeneous slab reactor.
We used the following dimensions in this calculation: a = 30 cm (fuel region) and b = 20 cm (reflector region). The eigenvalue obtained by the finite difference method is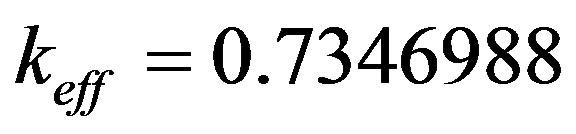 . Figures 5 and 6 show the results obtained for fast and thermal flux, respectively, comparing the analytical solution (Analytic) with the numerical methods of finite difference (FDM) and the nodal expansion method (NEM).
. Figures 5 and 6 show the results obtained for fast and thermal flux, respectively, comparing the analytical solution (Analytic) with the numerical methods of finite difference (FDM) and the nodal expansion method (NEM).
We can see that the results remained good for the two cases. This shows that when it is possible to obtain an analytical solution for a simplified geometry, the results obtained by the analytical solution are quite close to the
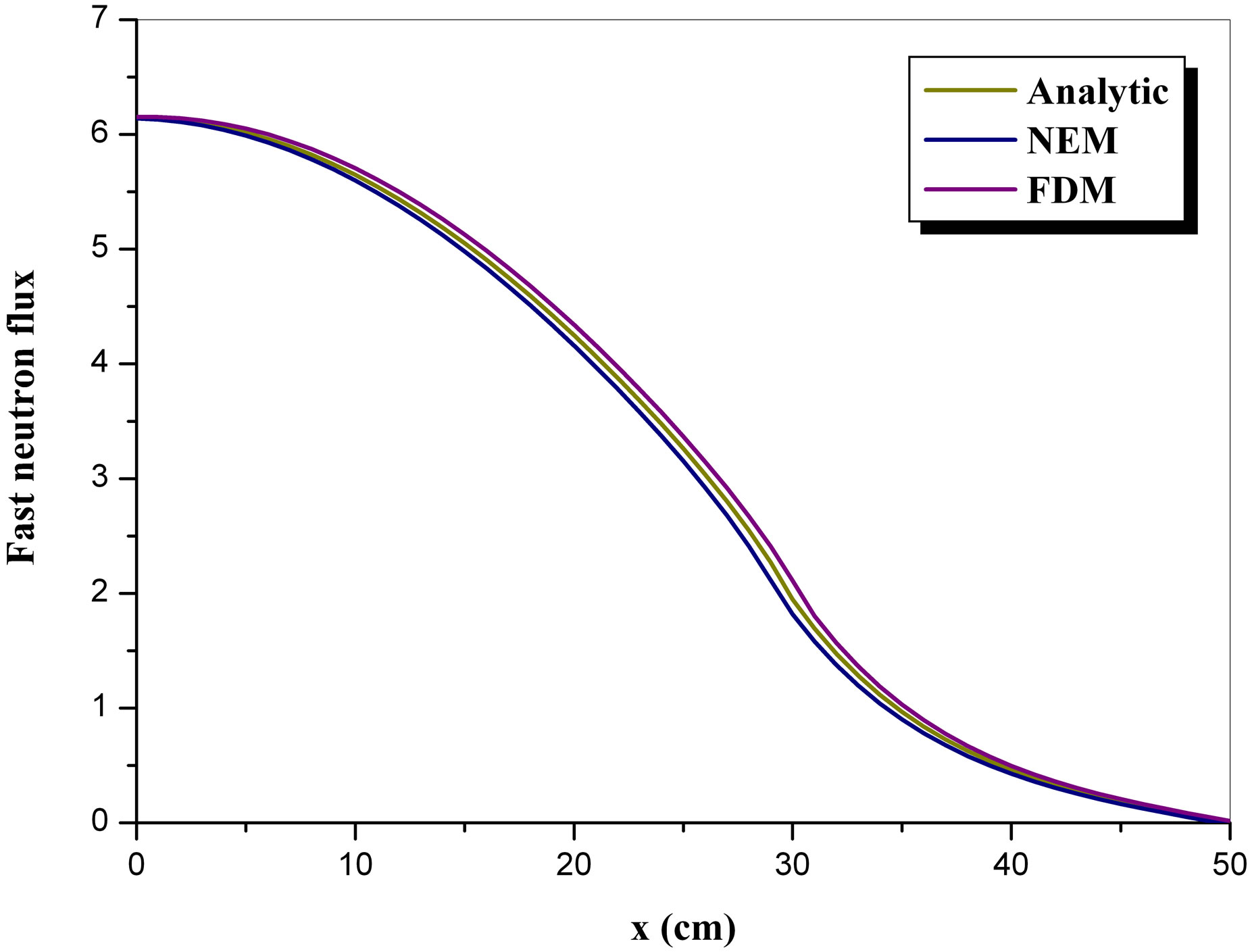
Figure 5. Comparison of fast neutron flux for two regions.
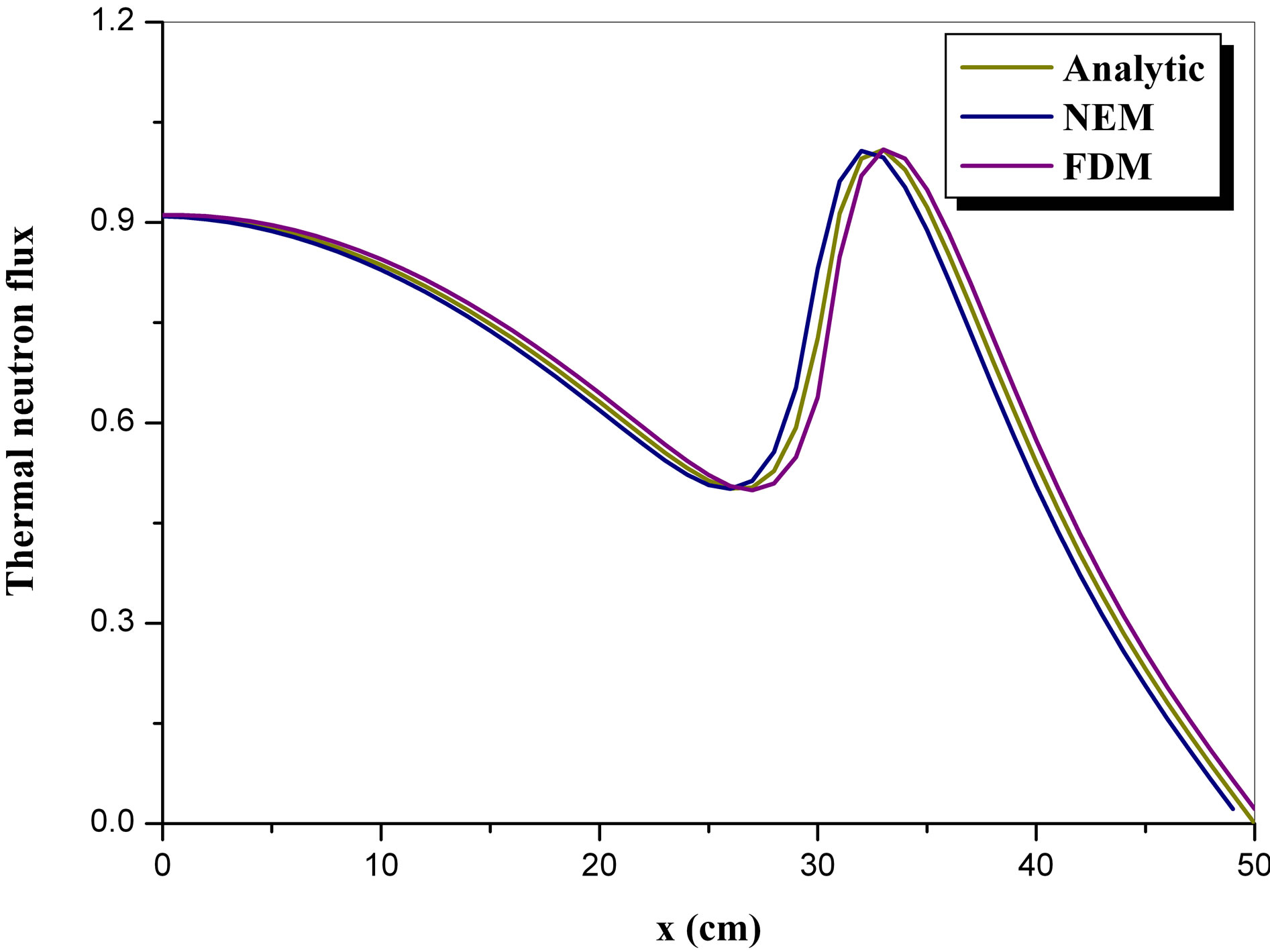
Figure 6. Comparison of thermal neutron flux for two regions.
numerical results. The information that the analytical solution needs to reconstruct the flux point-by-point that comes from the numerical method are: the eigenvalue keff that is an information intrinsic of the reactor due to its geometry and nuclear parameters and the initial flux 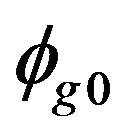 that is obtained by the numerical solution.
that is obtained by the numerical solution.
6. Conclusions
The objective of this work was to verify, when an analytical solution can be obtained, this solution can reproduce point-by-point the results of the numerical method, in this case, finite difference method (reference method). With this, some simplified cases were presented to compare analytical results with numerical ones. External data from the numerical method were incorporated as input data for the analytical solution, that were 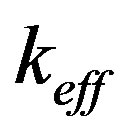 and the initial neutron flux. With such information, with the conditions of boundary and symmetry of the problem and with the nuclear parameters, it was possible to reconstruct the multigroup neutron flux in a slab reactor for the case of a single region (fuel) and two regions (fuel and reflector) where in both cases the analytical solution produced very satisfactory results.
and the initial neutron flux. With such information, with the conditions of boundary and symmetry of the problem and with the nuclear parameters, it was possible to reconstruct the multigroup neutron flux in a slab reactor for the case of a single region (fuel) and two regions (fuel and reflector) where in both cases the analytical solution produced very satisfactory results.
Based on the conclusions presented, it is hoped that the methodology implemented in this article can be extended to bi-dimensional cases of greater practical interest, as well as its use in the axial reconstruction [11] of the neutron flux in PWR reactors.
REFERENCES
- W. M. Stacey, “Nuclear Reactor Physics,” Wiley, New York, 2001.
- R. Boer and H. Finnemann, “Fast Analytical Flux Reconstruction Method for Nodal Space-Time Nuclear Reactor Analysis,” Annals of Nuclear Energy, Vol. 19, No. 10-12, 1992, pp. 617-628. doi:10.1016/0306-4549(92)90006-W
- H. G. Joo, J. I. Yoon and S. G. Baek, “Multigroup Pin Power Reconstruction with Two-Dimensional Source Expansion and Corner Flux Discontinuity,” Annals of Nuclear Energy, Vol. 36, No. 1, 2009, pp. 85-97. doi:10.1016/j.anucene.2008.10.003
- J. M. Aragones and N. Garcia-Herranz, “The Analytic Coarse-Mesh Finite Difference Method for Multi-Group and Multidimensional Diffusion Calculations,” Nuclear Science and Engineering, Vol. 157, No. 1, 2007, pp. 1-15.
- S. G. Baek, H. G. Joo and U. C. Lee, “Two-Dimensional Semi-Analytic Nodal Method for Multigroup Pin Power Reconstruction,” International Congress on Advances in Nuclear Power Plants (ICAPP 2007), Vol. 1, Nice, 13-18 May 2007, p. 1323.
- H. Finnemann, F. Bennewitz, and M. R. Wagner, “Interface Current Techniques for Multidimensional Reactor Calculations,” Atomkernenergie, Vol. 30, No. 2, 1977, pp. 123-128.
- R. D. Lawrence, “Progress in Nodal Methods for the Solution of the Neutron Diffusion and Transport Equations,” Progress in Nuclear Energy, Vol. 17, No. 3, 1986, pp. 271-301. doi:10.1016/0149-1970(86)90034-X
- A. C. Silva, F. C. Silva and A. S. Martinez, “Prediction of the neutrons subcritical multiplication using the diffusion hybrid equation with external neutron sources,” Annals of Nuclear Energy, Vol. 38, No. 7, 2011, pp. 1667-1675. doi:10.1016/j.anucene.2010.10.021
- J. J. Duderstadt and L. J. Hamilton, “Nuclear Reactor Analysis,” John Wiley and Sons, New York, 1976.
- O. Rübenkönig, “The Finite Difference Method an Introduction,” Albert Ludwigs University of Freiburg, Freiburg, 2006.
- L. Yu, D. Lu, S. Zhang and Y. Chao, “Group Decoupled Multi-Group Pin Power Reconstruction Utilizing Nodal Solution 1D flux Profiles,” Physor-2010, Pittsburg, 2010.
NOTES
*Corresponding author.

