American Journal of Operations Research
Vol.05 No.05(2015), Article ID:59840,14 pages
10.4236/ajor.2015.55036
An Inventory Model for Perishable Items with Time Varying Stock Dependent Demand and Trade Credit under Inflation
Sushil Kumar*, U. S. Rajput
Department of Mathematics & Astronomy, University of Lucknow, Lucknow, India
Email: *sushilmath4444@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 August 2015; accepted 20 September 2015; published 23 September 2015
ABSTRACT
In the classical inventory models, it is assumed that the retailer pays to the supplier as soon as he received the items and in such cases the supplier offers a cash discount or credit period (permissible delay) to the retailer. In this paper we presented an inventory model for perishable items with time varying stock dependent demand under inflation. It is assumed that the supplier offers a credit period to the retailer and the length of credit period is dependent on the order quantity. The purpose of our study is to minimize the present value of retailer’s total cost. Numerical examples are also given to demonstrate the presented mode.
Keywords:
Inventory, Deterioration, Perishable, Credit Period, Time Varying Stock Dependent Demand

1. Introduction
In the classical inventory models payment for the items paid by the supplier depends on the payment paid by the retailer and in such cases the supplier offers a fixed credit period to the retailer during which no interest will be charged by the supplier so there is no need to pay the purchasing cost by the retailer and after this credit period up to the end of a period interest charged and paid by the retailer. In such situations the retailer starts to accumulate revenue on his sale and earn interest on his revenue. If the revenue earned by the retailer up to the end of credit period is enough to pay the purchasing cost or there is a budget then the balance is settled and the supplier does not charge any interest, otherwise the supplier charges interest for unpaid balance after the credit period. The interest and the remaining payment are made at the end of replenishment cycle.
In traditional EOQ models the payment time does not affect the profit and replenishment policy. If we consider the inflation then order quantity and payment time can influence both the supplier’s and retailer’s decisions. A large pile of perishable foods such as fruits, vegetables, milk, bread, chocklet etc. attract the consumers to buy more. Buzacott [1] considered an EOQ model with different type of pricing policies under inflation. Silver and Peterson [2] developed an inventory model and show that the consumption rate is proportional to the displayed stock level. Baker and Urban [3] proposed an inventory model for deteriorating items with the demand rate is a polynomial function of instantaneous stock level. Mandal and Phaujdar [4] presented an inventory model for deteriorating items with stock level dependent consumption rate. Vrat and Padmanabhan [5] considered an inventory model with stock dependent demand under constant inflation rate. Padmanabhan and Vrat [6] developed an EOQ model for perishable products under stock dependent selling rate. Bose et al. [7] considered an inventory model for deteriorating items with time dependent demand and shortages under inflation and time discounting. Mandal and Maiti [8] developed an inventory model for damageable items with stock dependent demand and variable replenishment rate. Chung and Lin [9] determine an optimal replenishment policy for an inventory model of deteriorating items by considering inflation and credit period. Chang [10] proposed an EOQ model for deteriorating items under inflation and time discounting assuming that the supplier offers a trade credit policy if the retailer order size is larger than a certain level. Dye and Ouyang [11] developed an EOQ model for perishable items with stock dependent selling rate by allowing shortages. Hou [12] presented an inventory model for deteriorating items with stock dependent consumption rate and shortages under inflation and credit period. Jaggi et al. [13] determine an optimal ordering policy for deteriorating items under inflation induced demand. Sana and Chaudhuri [14] developed a deterministic EOQ model with stock dependent demand and delay in payments. Valliaththal and Uthayakumar [15] presented an inventory model for perishable items under stock and time dependent selling rate with shortages. Roy et al. [16] considered an inventory model for deteriorating items with stock dependent demand under fuzzy inflation and time discounting over a random planning horizon. Sana [17] proposed a lot size inventory model with stock dependent demand and time varying deterioration and partial backlogging. Chang et al. [18] determine an optimal replenishment policy for an inventory model of non-instantaneous deteriorating items with stock dependent demand. Sarkar et al. [19] presented an EMQ (economic manufacturing quantity) model of an imperfect production process with time dependent demand and time value of money under inflation. Yan [20] considered an EOQ model for perishable items with freshness dependent demand and partial backlogging. Nagrare and Dutta [21] developed a continuous review inventory model for perishable products with inventory dependent demand. Sana [22] proposed a control policy for a production system inflation assuming a stock dependent demand and sales team promotional effort.Shuai et al. [23] considered an inventory model for perishable products with stock dependent demand and trade credit under inflation.
Table 1 and Table 2 show the variation of the parameters r and M when 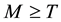 and Table 3 & Table 4 show the variation of parameters r and M when
and Table 3 & Table 4 show the variation of parameters r and M when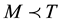 . Figure 1 & Figure 2 are correspond to the developed model. Figure 3 & Figure 4 show the variation of retailer’s total cost with respect to the parameters r and M when
. Figure 1 & Figure 2 are correspond to the developed model. Figure 3 & Figure 4 show the variation of retailer’s total cost with respect to the parameters r and M when 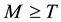 and Figure 5 & Figure 6 show the variation of retailer’s total cost with respect to the parameters r and M when
and Figure 5 & Figure 6 show the variation of retailer’s total cost with respect to the parameters r and M when .
.
In the present paper we presented an inventory model for perishable items with time varying stock dependent demand and trade credit under inflation. Although there are so many research papers related to the perishable
Figure 1. Corresponding to developed model.
Figure 2. With n cycles in the developed model.
Table 1. Variation of retailer’s total cost with respect to the change of parameter r.
Table 2. Variation of retailer’s total cost with respect to the change of parameter M.
Table 3. Variation of retailer’s total cost with respect to the change of parameter r.
Table 4. Variation of retailer’s total cost with respect to the change of parameter M.
Figure 3. Variation in TC with respect to r.
Figure 4. Variation in TC with respect to M.
Figure 5. Variation in TC with respect to r.
Figure 6. Variation in TC with respect to M.
products with stock dependent demand under inflation. This paper deals with the same type problem and it provides an approximate solution procedure of this problem for minimizing the present value of retailer’s total cost.
2. Assumptions and Notations
We consider the following assumptions and notations corresponding to the developed model
1) The demand rate  is
is 
2) 
3) 
4) 
5) 
6) M is the credit period.
7) T is the replenish cycle length.
8) r is the inflation rate.
9) 

10) C is the purchasing cost per unit.
11) P is the selling price per unit with
12) Q is the initial inventory level.
13) L is the planning horizon.
14) The supplier sells one single item to the retailer.
15) The items are replenished when the stock level becomes zero.
16) The supplier provides a credit period, which is dependent on the order quantity.
17) The lead time is zero.
18) Shortages are not allowed.
19) The inventory planning horizon is finite and the numbers of cycles are finite in the planning horizon.
20) I(t) is the inventory level at any time t.
3. Mathematical Formulation
Suppose an inventory system consists the maximum inventory level at any time t = 0 and due to both demand and deterioration the inventory level decreases in the interval


With the boundary condition
The equation (1) can also be written as

where
With the boundary condition
For a 2nd order approximation of 


Using the boundary condition, I(0) = Q the initial order quantity is

Now we discuss the following two cases
(1) 
3.1. Case I
When 
During the 1st cycle the present value of ordering cost is

During the 1st cycle the present value of purchasing cost is

During the 1st cycle the present value of holding cost is

Therefore during the 1st cycle the present value of retailer’s total cost is

Since there are m cycles in the planning horizon L then the present value of retailer’s total cost over the planning horizon L is

The necessary condition for 




3.2. Case II
When 
1) Let 
so in this case no interest will be charged by the supplier although the credit period M is smaller than the replenishment cycle length T so the present value of retailer’s total will be same as that in case I.

2) Let 
and the retailer has a budget to pay the remaining short purchasing cost so in this case there is still no interest charged by the supplier although the credit period M is smaller than the replenishment cycle length T so the present value of retailer’s total will be same as that in case I.

3) Let 
and the retailer has no budget to pay the remaining short purchasing cost so in this case for unpaid balance the interest will be charged by the supplier from M to T. The interest and the remaining payments are made at the end of replenishment cycle. So in this case the retailer’s total cost containing the ordering cost, holding cost, purchasing cost paid at M, the interest and the remaining payments are made at the end of replenishment cycle.
The present values of retailer’s ordering and holding are same cost as in case I
During the first cycle the purchasing cost paid at M is equal to the amount of revenue earned by the retailer up to M so

During the first cycle the present values of remaining payments and interest paid at the end of replenishment cycle are

During the 1st cycle the present value of retailer’s total cost is

Since there are m cycles in the planning horizon L then the present value of retailer’s total cost over the planning horizon L is

The necessary condition for 




4. Numerical Parameters
Let us consider the following parameters in the appropriate units
4.1. Numerical Example I
When 


Since
As we increase the parameter r then the value of total cost decreases.
As we increase the parameter M then the value of total cost decreases.
4.3. Numerical Parameters
Let us consider the following parameters in the appropriate units
4.4. Numerical Example II
When 




As we increase the parameter r then the value of total cost increases.
As we increase the parameter M then the value of total cost decreases.
5. Conclusion
In this paper, we proposed an inventory model for perishable items with time varying stock dependent demand under inflation and time discounting. In the numerical analysis we study the effect of the change of the parameters r and M on the optimal solution. From Table 1 and Table 2 we observe that as we increase the parameters r and M then the replenishment cycle length increases and the corresponding total cost decreases since the total cost decreases and the revenue increases on his sell to pay the purchasing cost and in the case when 
Cite this paper
SushilKumar,U. S.Rajput, (2015) An Inventory Model for Perishable Items with Time Varying Stock Dependent Demand and Trade Credit under Inflation. American Journal of Operations Research,05,435-449. doi: 10.4236/ajor.2015.55036
References
- 1. Buzacott, J.A. (1975) Economic Order Quantity Model under Inflation. Operational Research Quarterly, 26, 553-558.
http://dx.doi.org/10.2307/3008214 - 2. Silver, E.A. and Peterson, R. (1985) Decision Systems for Inventory Management and Production Planning. 2nd Edition, John Wiley & Sons, New York.
- 3. Baker, R.C. and Urban, T.L. (1988) A Deterministic Inventory System with an Inventory Level Dependent Demand Rate. Journal of Operational Research Society, 39, 823-831.
http://dx.doi.org/10.1057/jors.1988.142 - 4. Mandal, B.N. and Phaujdar, S. (1989) An Inventory Model for Deteriorating Items and Stock Dependent Consumption Rate. Journal of Operational Research Society, 40, 483-488.
http://dx.doi.org/10.1057/jors.1989.75 - 5. Vrat, P. and Padmanabhan, G. (1990) An Inventory Model with Stock Dependent Consumption Rate under Inflation. Engineering Costs and Production Economics, 19, 379-383.
http://dx.doi.org/10.1016/0167-188X(90)90068-S - 6. Padmanabhan, G. and Vrat, P. (1995) EOQ Models for Perishable Items with Stock Dependent Selling Rate. European Journal of Operational Research, 86, 281-292.
http://dx.doi.org/10.1016/0377-2217(94)00103-J - 7. Bose, S., Goswami, A. and Choudhuri, K.S. (1995) An EOQ Model for Deteriorating Items with Linear Time Dependent Demand Rate and Shortages under Inflation and Time Discounting. Journal of Operational Research Society, 46, 771-782.
http://dx.doi.org/10.1057/jors.1995.107 - 8. Mandal, M. and Maiti, M. (1999) An Inventory Model of Damageable Products Having Some Units in Hand with Stock Dependent Demand, Variable Replenishment Rate. Applied Mathematical Modeling, 23, 799-807.
http://dx.doi.org/10.1016/S0307-904X(99)00018-9 - 9. Chung, K.-J. and Lin, C.-N. (2001) An Optimal Replenishment Policy for an Inventory Model for Deteriorating Items with Time Discounting. Computers and Operations Research, 28, 67-83.
http://dx.doi.org/10.1016/S0305-0548(99)00087-8 - 10. Chang, C.T. (2004) An EOQ Model for Deteriorating Items under Inflation When Supplier Credits Linked to Order Quantity. International Journal of Production Economics, 88, 307-316.
- 11. Dye, C.Y. and Ouyang, L.Y. (2005) An EOQ Model for Perishable Items with Stock Dependent Selling Rate by Allowing Shortages,. European Journal of Operational Research, 163, 776-783.
http://dx.doi.org/10.1016/j.ejor.2003.09.027 - 12. Hou, K.L. (2006) An Inventory Model for Deteriorating Items with Stock Dependent Consumption Rate and Shortages under Inflation and Time Discounting. European Journal of Operational Research, 168, 463-474.
http://dx.doi.org/10.1016/j.ejor.2004.05.011 - 13. Jaggi, C.K., Aggarwal, K.K. and Goel, S.K. (2006) An Optimal Ordering Policy for an Inventory Model of Deteriorating Items under Inflation Induced Demand. International Journal of Production Economics, 103, 707-714.
http://dx.doi.org/10.1016/j.ijpe.2006.01.004 - 14. Sana, S.S. and Chaudhuri, K.S. (2008) A Deterministic EOQ Model for Deteriorating Items with Delay in Payments Offered by the Supplier. European Journal of Operational Research, 184, 509-533.
http://dx.doi.org/10.1016/j.ejor.2006.11.023 - 15. Valliathal, M. and Uthayakumar, R. (2009) An EOQ Model for Perishable Items with Stock and Time Dependent Selling Rate by Allowing Shortages. APRN Journal of Engineering and Applied Sciences, 4, 8-13.
- 16. Roy, A., Maiti, M.K., Kar, S. and Maiti, M. (2009) An Inventory Model for Deteriorating Items with Stock Dependent Demand under Fuzzy Inflation and Time Discounting over a Random Planning Horizon. Applied Mathematical Modeling, 33, 744-759.
http://dx.doi.org/10.1016/j.apm.2007.12.015 - 17. Sana, S.S. (2010) An Inventory Model for Time Varying Deteriorating Items with Optimal Selling Price and Lot Size by Allowing Shortages. Applied Mathematics and Computation, 217, 185-194.
http://dx.doi.org/10.1016/j.amc.2010.05.040 - 18. Chang, C.T., Teng, J.T. and Goyal, S.K. (2010) Optimal Replenishment Policies for Non Instantaneous Deteriorating Items with Stock Dependent Demand. International Journal of Production Economics, 123, 62-68.
http://dx.doi.org/10.1016/j.ijpe.2009.06.042 - 19. Sarkar, B., Sana, S.S. and Chaudhuri, K. (2011) An EMQ Model for an Imperfect Production Process for Time Varying Demand under Inflation and Time Value of Money. Expert Systems with Applications, 38, 13543-13548.
- 20. Yan, X. (2012) An EOQ Model for Perishable Items with Freshness Dependent Demand and Partial Backlogging. International Journal of Control and Automation, 5, 19-38.
- 21. Nagare, M. and Dutta, P. (2012) A Continuous Review Inventory Model for Perishable Products with Inventory Dependent Demand. Proceeding of the International Multi Conference of Engineers and Computer Scientists Hong-Kong, 14-16 March 2012, 1513-1517.
- 22. Sana, S.S. (2013) A Sales Team’s Initiatives and Stock Sensitive Demand under Production Control Policy. Economic Modeling, 31, 783-788.
http://dx.doi.org/10.1016/j.econmod.2013.01.026 - 23. Yang, S., Lee, C. and Zhang, A.M. (2013) An Inventory Model for Perishable Products with Stock Dependent Demand and Trade Credit under Inflation. Mathematical Problems in Engineering, 2013, 1-10.
http://dx.doi.org/10.1155/2013/702939
NOTES
*Corresponding author.

























