Intelligent Information Management, 2009, 1, 159-165
doi:10.4236/iim.2009.13023 Published Online December 2009 (http://www.scirp.org/journal/iim)
159
Software Selection in Manufacturing Industries
Using a Fuzzy Multiple Criteria Decision Making
Method, PROMETHEE
R. V. RAO, T. S. RAJESH
S. V. National Institute of Technology, Ichchanath, Surat, India
Abstract: This paper presents an effective decision making framework for software selection in manufactur-
ing industries using a multiple criteria decision making method, Preference Ranking Organization Method for
Enrichment Evaluations (PROMETHEE). The method is improved in the present work by integrating with
analytic hierarchy process (AHP) and the fuzzy logic. Fuzzy logic is introduced to handle the imprecision of
the human decision making process. The proposed decision making framework is practical for ranking com-
peting software products in terms of their overall performance with respect to multiple criteria. An example is
included to illustrate the approach.
Keywords: software selection, manufacturing industries, multiple criteria decision making, PROMETHEE,
fuzzy logic
1. Introduction
Application of software in design and manufacturing
processes is one of the resolutions many industries have
resorted to in the 21st century. This has been a result of
increased complexity of products, globalization, rapid
changes in technology, and so on. The idea was that the
application of software would increase the competitive
advantage of an industry. Various types of software are
used by the manufacturing industries, such as product
development process (PDP) software, product data man-
agement (PDM) software, product life-cycle manage-
ment (PLM) software, enterprise resource planning (ERP)
software, computer-aided design (CAD) software, com-
puter-aided manufacturing (CAM) software, etc. The
software used in various industries can be either COTS
or in-house developed. COTS is acronym for commercial
off-the-shelf, an adjective that describes software or
hardware products that are ready-made, and available for
sale to the general public. Given the high interest in mo-
tivation to the use of commercially available software in
manufacturing industries, the evaluation and selection of
COTS products is an important activity in software de-
velopment projects. Selecting an appropriate COTS
product is often a non-trivial task in which multiple cri-
teria need to be carefully considered. With so many cri-
teria to consider when selecting new software, help is
needed to focus on the essentials and to avoid the soft-
ware selection traps that many organisations fall into.
Clearly, software selection is not a well-defined or struc-
tured decision problem. The presence of multiple criteria
(both managerial and technical) will expand decisions
from one to many several dimensions, thus, increasing
the complexity of the solution process. It seems obvious
that the selection problem may not be solved simply by
grinding through a mathematical model or computer al-
gorithm. New approaches, which could handle multi-
criteria decision-making problems of choice and priori-
tization, to support these types of complex and unstruc-
tured selection problems are needed. Many decision
makers select COTS products according to their experi-
ence and intuition. However, this approach is obviously
subjective, and its weakness was addressed by Mikhailov
and Singh [1].
During the past two decades, there has been a steady
growth in the number of multiple criteria decision mak-
ing (MCDM) methods for assisting decision making with
multiple objectives. These MCDM methods allow deci-
sion makers to evaluate various competing alternative
courses of action to achieve a certain goal. Santhanam
and Kyparisis [2,3] proposed a non-linear programming
model to optimize resource allocation and their model
considered interdependencies between projects in the
information system selection process. Carney and Wall-
nau [4] observed that there are almost as many perspec-
tives on the topic of software evaluation as there are
evaluation techniques. The authors developed some basic
principles applicable for evaluation of commercial-off-

R. V. RAO ET AL. 160
the-shelf software. Sarkis and Sundarraj [5] discussed
about various factors for strategic evaluation of enter-
prise information technologies. Badri et al. [6] presented
a goal programming model to select an information sys-
tem project considering multiple criteria including bene-
fits, hardware, software and other costs, risk factors,
preferences of decision makers and users, completion
time, and training time constraints.
Morisio et al. [7] investigated COTS-based software
development within a particular NASA environment,
with an emphasis on the processes used. Fifteen projects
using a COTS-based approach were studied and their
actual process was documented. This process was evalu-
ated to identify essential differences in comparison to
traditional software development. The authors concluded
that the main differences, and the activities for which
projects require more guidance, were requirements defi-
nition and COTS selection, high level design integration
and testing.
The analytic hierarchy process (AHP) was widely used
by both researchers and practitioners in COTS selection
processes [8–13]. Lai et al. [8] reported the results of a
case study where the AHP technique was employed to
support the selection of a multimedia authorizing system
(MAS) in a group decision environment. Three MAS
products were identified and ultimately ranked using the
AHP.
Sarkis and Talluri [9] presented a decision framework
that could aid members of the supply chain and a supply
chain director in deciding which electronic commerce
technology media and software is most suitable for the
whole supply chain. The techniques used in this ap-
proach included both qualitative and quantitative meas-
urements for the evaluation or justification of these sys-
tems. The framework used an integrative set of models
based on the analytical hierarchy process and goal pro-
gramming.
Wei et al. [10] presented a comprehensive framework
for selecting a suitable enterprise resource planning (ERP)
system using AHP based approach. A real world example
was presented to demonstrate the feasibility of the frame-
work. Mulebeke and Zheng [11] carried out a case study
to introduce analytic network process (ANP) as a multi-
ple attribute strategic decision making approach to help
in the selection of appropriate software to suit the prod-
uct development process of a particular product.
Shyur [12] proposed different evaluation criteria and
the related attributes. The criteria (and the attributes) are:
cost (license fee, modular pricing, maintenance, docu-
mentation, consultant fee, resource utilization, conver-
sion cost, etc.), supplier’s support (vendor responsive-
ness, consulting, hot line, training, technical support
personnel, continuing enhancement, time sharing access,
warranty, documentation, financial stability, local branch
office, third vendor support, growth of customer base,
active R&D, etc.), technological risk (non-robust and
incomplete packages, complex and undefined, COTS-
to-legacy-system interfaces, middleware technology bugs,
poor custom code, and poor system performance, soft-
ware maturity, hardware maturity, etc.), closeness of fit
to the company’s business (main target, included func-
tionality, etc.), ease of implementation (shorter imple-
mentation time, user friendliness, multi- site implemen-
tation, etc.), flexibility to easy change as the company’s
business changes (adaptability, openness for customer
development, openness for working with other systems,
etc.) and system integration (internal connectivity, exter-
nal connectivity, etc.). Shyur (2006) modeled COTS
evaluation problem and proposed a five-phase COTS
selection model combining the techniques of analytic
network process (ANP) and modified TOPSIS. ANP was
used to determine the relative weights of multiple attrib-
utes. The modified TOPSIS approach was used to rank
the competing COTS products in terms of their overall
performance. However, the TOPSIS method can’t deal
with qualitative criteria.
Otamendi et al. [13] suggested a suitable software that
will help not only with the scheduling of resources but
also with their real time control during normal operations
of an airport in Spain. The selection process of the soft-
ware was based on the study of the capabilities of the
commercial and general-purpose simulation and visuali-
zation tools available as well as on the quantification of
user requirements and the development of trial versions.
AHP method was used to choose the platform, which
was composed of a simulation model developed in JAVA
and two visualization screens, one in JAVA and the other
in Visual Basic.
Even though certain methods, as described above,
were proposed in the past to address the issue of selec-
tion of an appropriate software for a given manufacturing
industrial application, these methods do not make a pro-
vision to consider the qualitative software selection crite-
ria (i.e. quantitative values are not available). There is a
need for a logical scientific method to guide user organi-
zations in taking a proper decision. This paper aims to
propose such a decision making method based on Pref-
erence Ranking Organization Method for Enrichment
Evaluations (PROMETHEE) in conjunction with AHP
for the problem of selecting appropriate software from
among the alternatives.
2. PROMETHEE Method
PROMETHEE method was introduced by Brans et al.
[14] and belongs to the category of outranking methods.
Like all outranking methods, PROMETHEE proceeds to
a pairwise comparison of alternatives in each single cri-
terion in order to determine partial binary relations de-
noting the strength of preference of an alternative a over
alternative b. In the evaluation table, the alternatives are

R. V. RAO ET AL. 161
evaluated on different criteria. These evaluations involve
mainly quantitative data. The implementation of PRO-
METHEE requires additional types of information,
namely:
 information on the relative importance that is the
weights of the criteria considered, and
 information on the decision maker preference func-
tion, which he/she uses when comparing the contribution
of the alternatives in terms of each separate criterion.
It may be added here that the original PROMETHEE
method can effectively deal mainly with quantitative
criteria. However, there exists some difficulty in the case
of qualitative criteria. In the case of a qualitative crite-
rion (i.e. quantitative value is not available); a ranked
value judgment on a fuzzy conversion scale is adopted in
this paper. By using fuzzy set theory, the value of the
criteria can be first decided as linguistic terms, converted
into corresponding fuzzy numbers and then converted to
the crisp scores. Rao (2007) had presented a logical ap-
proach based on the work of Cheng and Hwang (1992).
The presented numerical approximation system system-
atically converts linguistic terms to their corresponding
fuzzy numbers. It contains eight conversion scales and in
the present work, an eleven-point scale is considered for
better understanding and representation. Table 1 is sug-
gested which represents the selection criterion on a
qualitative scale using fuzzy logic, corresponding to the
fuzzy conversion scale as shown in Figure 1 and helps
the users in assigning the values. For more details, one
can refer to Chen and Hwang (1992). Once a qualitative
criterion is represented on a scale then the alternatives
can be compared with each other on this criterion in the
same manner as that for quantitative criteria.
The methodology presented in this paper for software
selection in the manufacturing environment using im-
proved PROMETHEE method is described below:
Step-1: Identify the selection criteria for the considered
decision making problem of software selection and short-
list the alternative softwares on the basis of the identified
Figure 1. Linguistic terms to fuzzy numbers conversion
criteria satisfying the requirements. A quantitative or
qualitative value or its range may be assigned to each
identified criterion as a limiting value or threshold value
for its acceptance for the considered application. An al-
ternative software with each of its criterion, meeting the
criterion, may be short-listed. The short-listed alterna-
tives may then be evaluated using the proposed method-
ology.
The values associated with the criteria for different al-
ternatives may be based on the available data or may be
the estimations made by the decision maker or a group of
decision makers. In the case of group decision making,
the values estimated by the decision makers for different
criteria for different alternatives may be different. In
such cases, the value of a criterion for an alternative may
be determined by averaging the estimated values given
by the group of decision makers for that criterion for that
alternative. The same averaging procedure may be car-
ried out for other criteria. Alternately, the group may
decide the values of criteria for different alternatives
based on group consensus.
Step-2:
1) After short-listing the alternatives, prepare a deci-
sion table including the measures or values of all criteria
for the short-listed alternatives.
2) The original PROMETHEE method has no system-
atic way of assigning the weights of relative importance
to the criteria. Hence, use of analytic hierarchy process
(AHP) is suggested in this paper to be used in conjunc-
tion with PROMETHEE for this purpose.
The steps are explained below:
a) Find out the relative importance of different criteria
with respect to the objective. To do so, one has to con-
struct a pair-wise comparison matrix using a scale of
relative importance. The judgments are entered using the
fundamental scale of the AHP. An attribute compared
with it is always assigned the value 1 so the main diago-
nal entries of the pair-wise comparison matrix are all 1.
The numbers 3, 5, 7, and 9 correspond to the verbal
judgments ‘moderate importance’, ‘strong importance’,
‘very strong importance’, and ‘absolute importance’
(with 2, 4, 6, and 8 for compromise between the previous
values). Assuming M criteria, the pair-wise comparison
of attribute i with attribute j yields a square matrix A1
where rij denotes the comparative importance of attribute
i with respect to attribute j. In the matrix, rij = 1 when i =
j and rji = 1 / rij
11 12131
21 22232M
31 32333
123
123
1
2
(1) 3
M
M
MM MMM
M Criterion
rrr r
rrr r
AIr rrr
rrr r M















 
 


R. V. RAO ET AL. 162
b) Find the relative normalized weight (Wj) of each at-
tribute by i) calculating the geometric mean of ith row
and ii) normalizing the geometric means of rows in the
comparison matrix. This can be represented as
M
GMi = {∏ rij}1/M (2)
j=1
and
M
Wj = GMi / ∑ GMi
(3)
i=1
The geometric mean method of AHP is used in the
present work to find out the relative normalized weights
of the attributes because of its simplicity and easiness to
find out the maximum Eigen value and to reduce the
inconsistency in judgments.
c) Calculate matrix A3 and A4 such that A3 = A1 x A2
and A4 = A3 / A2, where A2 = [W1, W2, ……, WM]T. Each
element of A4 is obtained by dividing each element of A3
by the corresponding element of A2.
d) Find out the maximum eigen value 
max (i.e. the av-
erage of matrix A4).
e) Calculate the consistency index CI = ( 
max – M) / (M
– 1). The smaller the value of CI, the smaller is the de-
viation from the consistency.
f) Obtain the random index (RI) for the number of at-
tributes used in decision making [15].
g) Calculate the consistency ratio CR = CI/RI. Usually,
a CR of 0.1 or less is considered as acceptable and it re-
flects an informed judgment that could be attributed to
the knowledge of the analyst about the problem under
study.
Step-3: After calculating the weights of the criteria us-
ing AHP method, the next step is to have the information
on the decision maker preference function, which he/she
uses when comparing the contribution of the alternatives
in terms of each separate criterion.
The preference function (Pi) translates the difference
between the evaluations obtained by two alternatives (a1
and a2) in terms of a particular criterion, into a prefer-
ence degree ranging from 0 to 1. Let Pi, a1a2 be the pref-
erence function associated to the criterion ci.
Pi,a1a2= Gi[ci(a1)−ci(a2)] (4)
0≤Pi,a1a2 ≤1 (5)
where Gi is a non-decreasing function of the observed
deviation (d) between two alternatives a1 and a2 over the
criterion ci. In order to facilitate the selection of a spe-
cific preference function, six basic types were proposed
[14,17]. These include “usual function”, “linear func-
tion”, “U-shape function”, “V-shape function”, “level
function” and “Gaussian function”. Preference “usual
function” which is equal to the simple difference be-
tween the values of the criterion ci for alternatives a1 and
a2 is adapted in this paper because of its simplicity. For
other preference functions, no more than two parameters
(threshold q, p or s) have to be fixed. Indifference
threshold ‘q’ is the largest deviation to consider as negli-
gible on that criterion and it is a small value with respect
to the scale of measurement. Preference threshold ‘p’ is
the smallest deviation to consider decisive in the prefer-
ence of one alternative over another and it is a large
value with respect to the scale of measurement. Gaussian
threshold ‘s’ is only used with the Gaussian preference
function. It is usually fixed as an intermediate value be-
tween indifference and a preference threshold.
Let us suppose that the decision maker has specified a
preference function Pi and weight wi for each criterion ci
(i = 1, 2, …, M) of the problem. The multiple criteria
preference index Пa1a2 is then defined as the weighted
average of the preference functions Pi:
M
Пa1a2 = ∑ wi Pi,a1a2 (6)
i=1
Пa1a2 represents the intensity of preference of the deci-
sion maker of alternative a1 over alternative a2, when
considering simultaneously all the criteria. Its value
ranges from 0 to 1. This preference index determines a
valued outranking relation on the set of actions. As an
example, the schematic calculation of the preference
indices for a problem consisting of 3 alternatives and 4
criteria is given in Figure 2.
For PROMETHEE outranking relations, the leaving
flow, entering flow and the net flow for an alternative ‘a’
belonging to a set of alternatives A are defined by the
following equations:
φ+(a) = ∑ Πxa (7)
x ε A
φ-(a) = ∑ Πax (8)
x ε A
φ(a) = φ+(a) - φ-(a) (9)
φ+(a) is called the leaving flow, φ-(ai) is called the en-
tering flow and φ(ai) is called the net flow. φ+(a) is the
4
П31 = ∑ wi Pi,31
i=1
Figure 2. Preference indices for a problem consisting of 3
alternatives and 4 criteria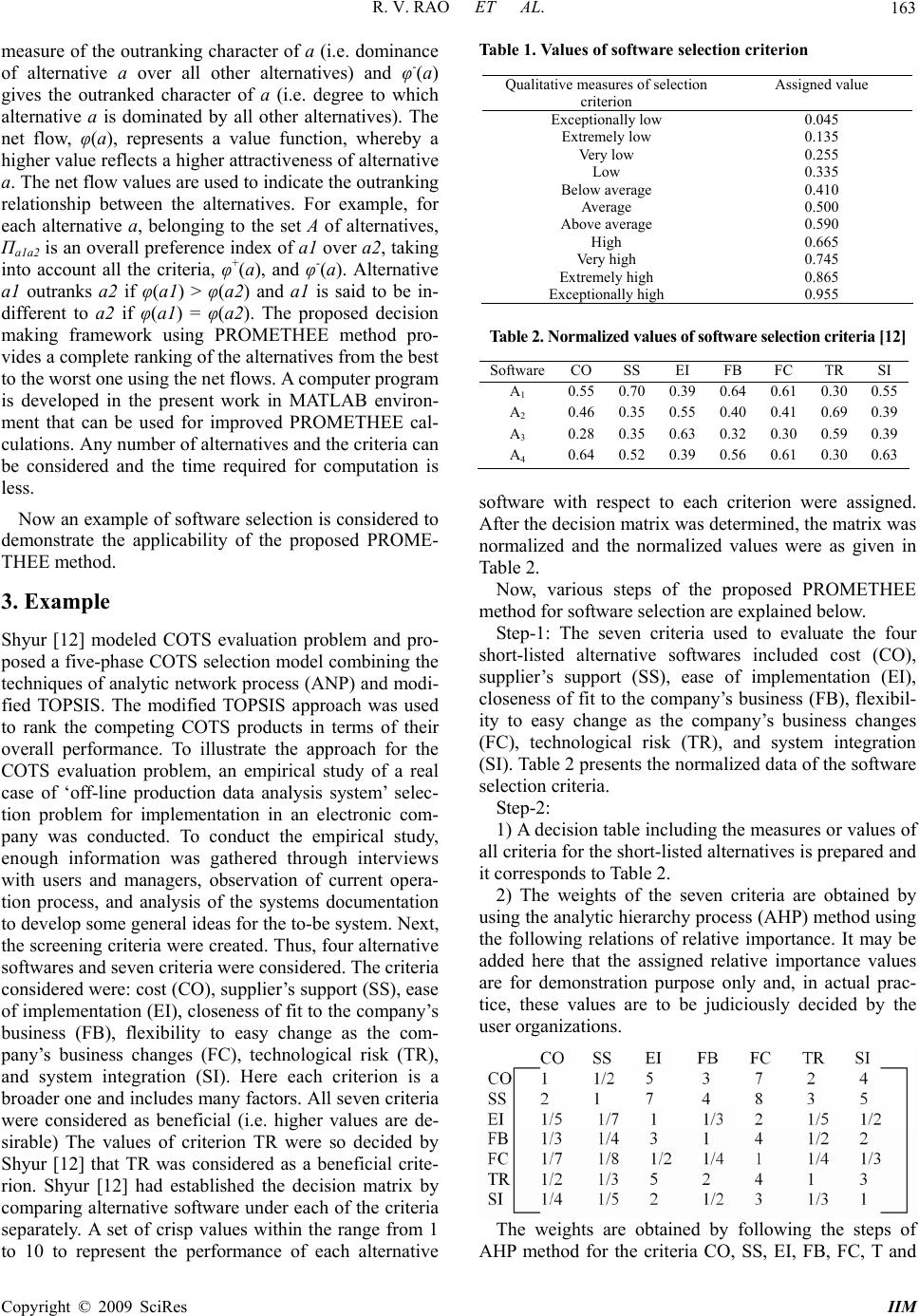

R. V. RAO ET AL. 163
measure of the outranking character of a (i.e. dominance
of alternative a over all other alternatives) and φ-(a)
gives the outranked character of a (i.e. degree to which
alternative a is dominated by all other alternatives). The
net flow, φ(a), represents a value function, whereby a
higher value reflects a higher attractiveness of alternative
a. The net flow values are used to indicate the outranking
relationship between the alternatives. For example, for
each alternative a, belonging to the set A of alternatives,
Пa1a2 is an overall preference index of a1 over a2, taking
into account all the criteria, φ+(a), and φ-(a). Alternative
a1 outranks a2 if φ(a1) > φ(a2) and a1 is said to be in-
different to a2 if φ(a1) = φ(a2). The proposed decision
making framework using PROMETHEE method pro-
vides a complete ranking of the alternatives from the best
to the worst one using the net flows. A computer program
is developed in the present work in MATLAB environ-
ment that can be used for improved PROMETHEE cal-
culations. Any number of alternatives and the criteria can
be considered and the time required for computation is
less.
Now an example of software selection is considered to
demonstrate the applicability of the proposed PROME-
THEE method.
3. Example
Shyur [12] modeled COTS evaluation problem and pro-
posed a five-phase COTS selection model combining the
techniques of analytic network process (ANP) and modi-
fied TOPSIS. The modified TOPSIS approach was used
to rank the competing COTS products in terms of their
overall performance. To illustrate the approach for the
COTS evaluation problem, an empirical study of a real
case of ‘off-line production data analysis system’ selec-
tion problem for implementation in an electronic com-
pany was conducted. To conduct the empirical study,
enough information was gathered through interviews
with users and managers, observation of current opera-
tion process, and analysis of the systems documentation
to develop some general ideas for the to-be system. Next,
the screening criteria were created. Thus, four alternative
softwares and seven criteria were considered. The criteria
considered were: cost (CO), supplier’s support (SS), ease
of implementation (EI), closeness of fit to the company’s
business (FB), flexibility to easy change as the com-
pany’s business changes (FC), technological risk (TR),
and system integration (SI). Here each criterion is a
broader one and includes many factors. All seven criteria
were considered as beneficial (i.e. higher values are de-
sirable) The values of criterion TR were so decided by
Shyur [12] that TR was considered as a beneficial crite-
rion. Shyur [12] had established the decision matrix by
comparing alternative software under each of the criteria
separately. A set of crisp values within the range from 1
to 10 to represent the performance of each alternative
Table 1. Values of software selection criterion
Qualitative measures of selection
criterion
Assigned value
Exceptionally low 0.045
Extremely low 0.135
Very low 0.255
Low 0.335
Below average 0.410
Average 0.500
Above average 0.590
High 0.665
Very high 0.745
Extremely high 0.865
Exceptionally high 0.955
Table 2. Normalized values of software selection criteria [12]
SoftwareCOSS EI FB FC TR SI
A1 0.55 0.70 0.39 0.64 0.61 0.300.55
A2 0.46 0.35 0.55 0.40 0.41 0.690.39
A3 0.28 0.35 0.63 0.32 0.30 0.590.39
A4 0.64 0.52 0.39 0.56 0.61 0.300.63
software with respect to each criterion were assigned.
After the decision matrix was determined, the matrix was
normalized and the normalized values were as given in
Table 2.
Now, various steps of the proposed PROMETHEE
method for software selection are explained below.
Step-1: The seven criteria used to evaluate the four
short-listed alternative softwares included cost (CO),
supplier’s support (SS), ease of implementation (EI),
closeness of fit to the company’s business (FB), flexibil-
ity to easy change as the company’s business changes
(FC), technological risk (TR), and system integration
(SI). Table 2 presents the normalized data of the software
selection criteria.
Step-2:
1) A decision table including the measures or values of
all criteria for the short-listed alternatives is prepared and
it corresponds to Table 2.
2) The weights of the seven criteria are obtained by
using the analytic hierarchy process (AHP) method using
the following relations of relative importance. It may be
added here that the assigned relative importance values
are for demonstration purpose only and, in actual prac-
tice, these values are to be judiciously decided by the
user organizations.
The weights are obtained by following the steps of
AHP method for the criteria CO, SS, EI, FB, FC, T and

R. V. RAO ET AL. 164
SI are 0.242, 0.360, 0.042, 0.102, 0.030, 0.157 and 0.067
respectively and the consistency ratio (CR) is less than
0.1. Thus, there is good consistency Shyur et al. [12]
obtained the same weights using ANP method in their
approach. To compare the results of the proposed PRO-
METHEE method, the same weights have been adopted
in the present example.
Step-3: After calculating the weights of the criteria us-
ing AHP method, the next step is to have the information
on the decision maker preference function, which he/she
uses when comparing the contribution of the alternatives
in terms of each separate criterion. Let the decision
maker uses the preference “usual function”. The prefer-
ence function (Pi) translates the difference between the
evaluations obtained by two alternatives (a1 and a2) in
terms of a particular criterion, into a preference degree
ranging from 0 to 1. If two alternatives have a difference
d≠0 in criterion cj, then a preference value P
i ranging
between 0 and 1 will be assigned to the ‘better’ alterna-
tive whereas the ‘worse’ alternative receives a value 0. If
two criteria have a zero difference, they are indifferent
which results in an assignment of 0 to both alternatives.
The pairwise comparison of criterion CO gives the ma-
trix shown in Table 3. The alternative software having
comparatively high value of CO is said to be ‘better’ than
the other. Similarly, the pairwise comparisons of the four
alternatives with respect to other criteria are made, but
not shown here for space reasons.
Table 4 is prepared which shows the resulting prefer-
ence indices as well as leaving, entering, and net flows of
the alternatives of Table 2. The preference indices are
calculated based on Equation (9) and the leaving, enter-
ing, and net flows of the alternatives are calculated based
on Equations (7), (8), and (9) respectively. From the val-
ues of software ranking, software A1 is understood as the
best choice among the considered software alternatives
Table 3. Preference values resulting from the pairwise
comparisons of the alternatives A1 to A4 with respect to
criterion CO
Software A1 A
2 A 3 A 4
A1 --- 1 1 0
A2 0 --- 1 0
A3 0 0 --- 0
A4 1 1 1 ---
Table 4. Resulting preference indices as well as leaving,
entering, and net flows
Π A1 A
2 A 3 A 4 φ+(a) φ(a) Ranking
A1 --- 0.799 0.799 0.462 2.06 1.3591
A2 0.197 --- 0.529 0.197 0.923 -0.7153
A3 0.197 0.04 --- 0.197 0.434 -1.6934
A4 0.307 0.799 0.799 --- 1.905 1.0492
φ-(a) 0.701 1.638 2.127 0.856
for the given software selection problem under consid-
eration. However, these results differ from the results
presented by Shyur [12]. Using modified TOPSIS pro-
cedure, Shyur [12] obtained the following ranking for the
considered softwares: A4= 0.652, A1=0.645, A2=0.433,
and A3=0.236. However, Shyur [12] had committed some
mistakes in computing the closeness coefficient values of
the alternative software. Removal of those mistakes
would lead to the following ranking: A1= 0.6908, A4=
0.5520, A2=0.3556 and A3=0.2261. This also suggests A1
as the best choice. Thus, the results proposed by PRO-
METHEE method are justified and reliable. It may be
added here that Shyur [12] had not considered any quali-
tative criteria in the considered problem. The TOPSIS
method used by Shyur [12] can’t deal with qualitative
criteria. However, the proposed PROMETHEE method
can easily deal with such qualitative criteria using Table 1.
4. Conclusions
The selection of suitable software would increase the
competitive advantage of an industry. This paper has
presented the details of a decision making framework for
software selection in manufacturing industries using
PROMETHEE method in conjunction with AHP method.
The proposed PROMETHEE method is a fairly simple
and therefore transparent for decision makers and stake-
holders who are often non-experts. Furthermore, the pa-
per suggests ranked value judgments on a fuzzy conver-
sion scale to represent the qualitative software selection
criterion. The proposed decision making framework us-
ing PROMETHEE method can be extended to any type
of decision making problem involving any number of
criteria and alternatives.
5. Acknowledgement
The authors acknowledge the financial support of Coun-
cil of Scientific and Industrial Research (CSIR) New
Delhi, India to carry out this work.
REFERENCES
[1] L. Mikhailov and M. G. Singh, “Fuzzy analytic network
process and its application to the development of decision
support systems,” IEEE Transactions on Systems, Man,
and Cybernetics, Part C. Applications and Reviews, Vol.
33, No. 1, pp. 33–41, 2003.
[2] R. Santhanam and G. J. Kyparisis, “A decision model for
interdependent information system project selection,”
European Journal of Operational Research, Vol. 89, No. 2,
pp. 380–399, 1996.
[3] R. Santhanam and G. J. Kyparisis, “A multiple criteria
decision model for information system project selection,”
Computers & Operations Research, Vol. 22, No. 8, pp.
807–818, 1995.

R. V. RAO ET AL. 165
[4] D. J. Carney and K. C. Wallnau, “A basis for evaluation
of commercial software. information and software tech-
nology,” Information and Software Technology, Vol. 40,
No. 14, pp. 851–860, 1998.
[5] J. Sarkis and R. P. Sundarraj, “Factors for strategic
evaluation of enterprise information technologies,” Inter-
national Journal of Physical Distribution & Logistics
Management, Vol. 30, No. 3, pp. 196–220, 2000.
[6] M. A. Badri, D. Davis, and D. Davis, “A comprehensive
0–1 goal programming model for project selection,” In-
ternational Journal of Project Management, Vol. 19, No. 4,
pp. 243–252, 2001.
[7] M. Morisio, C. B. Seaman, V. R. Basili, A. T. Parra, S. E.
Kraft, and S. E. Condon, “COTS-based software devel-
opment: processes and open issues,” Journal of Systems
and Software, Vol. 61, No. 3, pp. 189–199, 2002.
[8] V. S. Lai, K. W. Bo, and W. Cheung, “Group decision
making in a multiple criteria environment: A case using
the AHP in software selection,” European Journal of Op-
erational Research, Vol. 137, No. 1, pp. 34–144, 2002.
[9] J. Sarkis and S. Talluri, “Evaluating and selecting e-com-
merce software and communication systems for a supply
chain,” European Journal of Operational Research, Vol.
159, No. 2, pp. 318–329, 2004.
[10] C. C. Wei, C. F. Chien, and M. J. J. Wang, “An AHP-
based approach to ERP system selection,” International
Journal of Production Economics, Vol. 96, No. 1, pp. 47–
62, 2005.
[11] J. A. W. Mulebeke, L. Zheng, “Analytical network proc-
ess for software selection in product development,” Jour-
nal of Engineering and Technology Management, Vol. 23,
No. 4, pp. 337–352, 2006.
[12] H. J. Shyur, “COTS evaluation using modified TOPSIS
and ANP,” Applied Mathematics and Computation, Vol.
177, No. 1, pp. 251–259, 2006.
[13] J. Otamendi, J. M. Pastor, and A. Garcı´a, “Selection of
the simulation software for the management of the opera-
tions at an international airport,” Simulation Modelling
Practice and Theory, Vol. 16, No. 8, pp. 1103–1112, 2008.
[14] J. P. Brans, B. Mareschal, and P. Vincke, “PROMETHEE:
A new family of outranking methods in multicriteria
analysis,” Operational Research, Vol. 3, pp. 477–490.
1984.
[15] T. L. Saaty, “Fundamentals of decision making and prior-
ity theory with AHP,” RWS Publications, Pittsburg, 2000.
[16] R. V. Rao, “Decision making in the manufacturing envi-
ronment using graph theory and fuzzy multiple attribute
decision making methods,” Springer-Verlag, London,
2007.
[17] O. Marinoni, “A stochastic spatial decision support sys-
tem based on PROMETHEE,” International Journal of
Geographical Information Science, Vol. 19, No. 1, pp.
51–68, 2005.