J. Software Engineering & Applications, 2009, 2: 309-315
doi:10.4236/jsea.2009.25040 Published Online December 2009 (http://www.SciRP.org/journal/jsea)
309
Responsiveness Improvement of Idling Speed
Control for Automotive Using SMC
Yang ZHANG1, Nobuo KURIHARA2, Hiroyuki YAMAGUCHI3
1Doctor of Science Program in Mechanical Systems, Hachinohe Institute of Technology, Hachinohe, Japan; 2Graduate School of
Engineering, Hachinohe Institute of Technology, Hachinohe, Japan; 3Department of System and Information, Hachinohe Institute of
Technology, Hachinohe, Japan.
Received August 8th, 2009; revised September 8th, 2009; accepted September 15th, 2009.
ABSTRACT
To improve the responsiveness of engine speed control to disturbances, robust controls were investigated by simulation.
The intake air control system of a gasoline engine is a typical nonlinear system, and the disturbances and parameter
perturbations are generally regarded as being the unstable factors with regard to engine control. In this paper, a
Mean-Value Engine Model (MVEM) with disturbances and parameter perturbations is investigated using Sliding Mode
Control (SMC), which is a form of variable structure control, with a view to address instability in the idle speed control
process. The simulation results confirmed that, compared with a conventional PI (Proportional-Integral) controller, the
stability of the idle speed for an engine that is being subjected to disturbances, parameter variations and background
noise is greatly improved by the application of SMC.
Keywords: Gasoline Engine, Intake Air Control, Sliding Mode Control, Simulation
1. Introduction
Since the beginning of the 21st century, environmental
and energy problems have been becoming increasingly
serious. A lack of fuel economy for automobiles is con-
sidered to be the main cause of the global energy crisis,
and this issue needs to be addressed. Idle speed is the
minimum operating speed of a combustion engine [1].
The period at idle occupies 30% of driving time for ur-
ban traffic. Furthermore, if the idle speed can be reduced
to 100 rpm (revolutions per minute) by improving the
control method, fuel consumption will be reduced by 2 to
5%. Therefore, significant fuel economy and emissions
improvements can be achieved by lowering the idle
speed of an engine. In order to achieve a relatively lower
idle speed while at the same time preventing the engine
from stalling, it is necessary to maintain a stable idle
speed in the presence of both known disturbances (e.g.
stationary steering and evaporation-gas purge) and un-
known disturbances. The automotive engine is a typical
nonlinear, time-delay, time-varying parameter system.
Recently there are many studies that apply control theo-
ries such as LQG, PID, and adaptive control to idle-speed
control [2]. In particular, because Variable structure con-
trol is suitable for linear and nonlinear, continual and
discrete, certain and uncertain systems, the application of
sliding mode control is regarded as the solution to the
problem of improving the idle-speed control. Neverthe-
less there are some studies are applying this theory [3,4].
However, idle-speed control is supposed to be investi-
gated practically.
In this paper, idle speed control was studied based on
a non-linear gasoline engine model. As the PID (pro-
portional–integral–derivative) controller is usually used
for idle speed control, the PID control and sliding mode
control (SMC) were employed to improve idle-speed
control. The several disturbances such as control input
disturbance, torque disturbance and fuel disturbance
were added in the engine model to certify the respon-
siveness and stability of two control methods. And the
operation of the sudden start also was also studied un-
der the fuel disturbance. The system is simulated by
MATLAB /Simulink. Relying on result of simulations,
the robustness of idle-speed control was improved by
using SMC.
2. Idle Speed Control System
In this paper, we used an idle speed control system which
was built based on the mean value engine model (MVEM)
[5]. The model consists of three units: an intake manifold
unit, a fuel mass unit, and a crankshaft unit. Because idle
speed control is the subject of this study, an electronic

Responsiveness Improvement of Idling Speed Control for Automotive Using SMC 310
Figure 1. Engine model for idle speed system
throttle is necessary. The usual control process for idle
speed is illustrated as follows. The intake air flow is ad-
justed to achieve the set point for the engine speed by
adjusting the angle and position of the electronic throttle.
The crank angle sensor detects the engine speed, and the
angle of the electronic throttle depends on the controller
in the engine control unit. Next, the amount of air sup-
plied to the cylinder is adjusted using the electronic
throttle. Once that has been done, an amount of fuel pro-
portionate to the air flow is injected into the cylinder.
Thus, the torque produced by fuel combustion maintains
a constant engine speed. A model of an idle speed control
system is shown in Figure 1.
Next, we will describe the three parts of the engine
model by providing the equations we used. The main
initial parameters of the engine model were as follows:
the engine displacement (Vd) is 1.3 L; the fuel energy
constant (Hu) was 43000 K J/kg; the gas constant of air
(R) was 0.00287 m2bar/k.kg; the atmospheric tempera-
ture (Ta) was 293 K; the intake manifold volume Vi was
0.000564 m3 the atmospheric pressure (Pa) was 1.013 bar;
and the moment of engine inertia was 5.2638 kgm2. Here
we considered four factors that can easily make idle
speed control unstable: torque disturbance, fuel vapor
disturbance, control input disturbance, and parameter
errors.
2.1 Crankshaft Block

ui ffpd
n = HmInPPPIn  
 (1)
The variable n in Equation (1) is the engine speed (the
unit used was set at rpm/1000); ηi is the thermal effi-
ciency; and Pf , Pp and Pb are frictional power, pumping
power, and load power, respectively.

036
0.392
n1 n



inp
=
= 0.015+0.558


 
2
2
2
0.392
0.0171 1.740.745
0.00048
pii
mbt mbt
=0.827+0.528P P
=
=0.7+0.024




 


 
Pf , Pp and Pb are calculated using the three empirical
equations below.

23
2
3
1 673
09
f
P.
P.
PM

0 2720 0135
69 0206
260
pi i
bb b
n.n. n
nP.nP
n Kn

 


(2)
Here, Pi is the manifold pressure; θ is the ignition an-
gle; θmbt is the mean best torque spark advance; λ is the
excess air coefficient; and Mb and Kb are both for the
torque load.
2.2 Fuel Block



  
2
1
0 2270 0550 68
1 350 06721 680 8250 060150 56
fffiff f
fv fi
i
fi
mXmm
mXm
X.P.n.
..n.P..n..




 
  
 

(3)
Here,
f
f
m
 is the evaporation fuel in the cylinder;
is the injected fuel; is the gasified fuel;
is the total amount of fuel in the cylinder; X is the coeffi-
cient of the fuel deposit; and is the time constant for
fuel evaporation.
fi
m
fv
m


f
m

f
2.3 Manifold Block


iiatapii ii
PRTm mVPT/T

 (4)
Here, is the temperature in the manifold; is
the intake air which passes through the throttle; and
is the cylinder intake air.
i
Tat m

m
ap
atis ai
mmm



(5)
where is the intake air that passes through the
by-pass valve
is
m





12
0 39880 01
ai r
m.uP.

 
 (6)
Here, is the intake air that passes through the
throttle.
ai
m







2
111 407318004087180u.cosu .cosu

  



2
2
04125
10 4125
104125
00 4125
r
r
r
r
P. P.
P.
P.











(7)

Responsiveness Improvement of Idling Speed Control for Automotive Using SMC311
Here,

u is the opening of the throttle and r
P
ratio of to
Wher
is the
i
P
e
a P.
v

is the engine volumetric efficiency.

2
2 0075
4
vi
i
P
TR m
 




095
0 14
a patiataiii
.mT .mTTPV

 

3. Lineariz
As is well known, the engine model is a typical n-
inear system. For the following design for SMC, we
needed to linearize the engine model to a state-space
ion point. In this case, we selected
..
ation
no
equation at the operat
an engine speed of n and manifold pressure of i P as
two states. Here,

u is the input of advance angle igni-
tion and

u is the input of the throttle, and both were
provisionally considered as control inputs.
  
 
 


 
1
2
110
i
u
xn
xu
P xu
Ax Bx
Ax Bx
2
2
2
1
21
2
12
0
018410 0390 31780 05160 0026
61 8951815 521 397
680 7
ii
i
np ap i
Bx
Ax
xA
x Bxu
A
x.P.nP. .n.n
Ax.nP.. n
Bxm.nB xRTV




  




 


(8)
Having sorted out the affine non-linear equations as
stated above, we then addressed the target operation
point (xd), which is given as follows:




 

  
 

 
d
d
n
xP


 id
Therefore, the engine model is linearized in the vicin-
ity of xd .
(9)
111211 12
d
212221 22
d
x
xxuuux AxBu
a
AB
  


 


a bb  
(10)
aa bb
 
Next, w


e substituted the tangent line for the curved
line according to the affine non-linear equation.
1
1
1
1
n
n
dd
x, u
nn
11
1
1
11
12
21
2
22
12 21
12
22
0 0390 05160 0052
0 18410 0039
0 0390 05160 0052
61 89518
0
680 7
1552
dd
d
n
x,u
nn
n
d
d
d
d
ix
np ap
ff
uu
f
Buff
uu
a.. .
a. .n
a.. .
a. n
P
bb
bm.n
b















 
 
 










n
n
(11)
As a result, we were able to obtain the final matrices
for A and B of the linearized model at two certain values
of the abovementioned states.
4. PID Control Design
In the paper, we employed PI controller shown in Figure
2.
Design
ucture control in which the
dynamic system to slide along the re-
n important, ro-
The gain of Kp and Ki are determined by the Ziegler-
Nichols method.
5. Sliding Mode Control
SMC is a type of variable str
dynamics of a nonlinear system are altered by the appli-
cation of a high-frequency switching control [6]. In other
words, SMC uses practically infinite gain to force the
trajectories of a
stricted sliding mode subspace. This is a
bust control approach that provides an adaptive approach
to tackling the parametric system, uncertain parametric
system, and uncertain disturbance system. If a switching
surface is appropriately designed with desirable charac-
teristics, the system will exhibit desirable behavior when
confined to this switching surface. To pursue the target
value, idle-speed control can be shown as a servo system.
Thus, the sliding mode for a single-input single-output
f
f
x
x
f
Ax
f
f
x
x

















Figure 2. Block diagram of PI controller

Responsiveness Improvement of Idling Speed Control for Automotive Using SMC 312
Figure 3. Block diagram of SMC
system has been made into the block diagram shown in
Figure 2, which illustrates a closed-loop SMC. The con-
trol input is the sum of the linear and non-linear inputs.
Here, nd is the target engine speed, n is the actual engine
speed, and the four kinds of disturbances we have consid-
ered in this paper have also been added in the Figure 3.
5.1 Controller
In this paperngle of the
rottle as the control input. Consequently, the following
, we are only considering the a
th
system is considered.
1112 11 12
21 22 2222
12 11 12
21 2222 i
xxb aa u
aa xxb
b
naa u
Paa b


  

  
  
  

  
 
ly SMC to the servo system, an expan-
(13)
The expansion servo system is given
below.


(12)
In order to app
sion system is used in which a new state, z, is assumed as
the value for the integration of the difference between the
target value and input. The variable z is defined in Equa-
tion (13) below.
1d
zrx nn 

in Equation (14)
111121
21 2222 22
00 0
00
0100 1zz
x
aa xur
aa b
xx


  
 

  


(14)
Equation (14) can be rewritten as follows:

  
 


x
Ax
Bu Er (15)
The switching function is as follows:

1
2
z
x
Sx Sx
x


 




(16)
The design for the switching surface is described late.
When the system is in sliding mode, the switchin
tion is as follows:
g func-


0x 

(17)
characteristic is exhibite
hy
When the system is in sliding mode state, the dynamic
d. When above the switching
per-plane, the system maintains 0


. Hence, by
using xS, substituting Equation (15) into 0





gives:
0eq SAx SBur SE

 (18)
Taking the control law as:
 
1
eq r
uSBSAxSE


 (19)
Equation (19) gives th
servo system with sliding
the switc
s give
where P is the positive definite soluti
eq
e equivalent linear control of a
mode.
5.2 Hyper-Plane
For the system stability margin, hing hyper-
plane S in as follows:
T
SBP (20)
on of the Riccati
uations, so that:
0
TT
PAA PPBBPQ

AAI





Where
(21)

is the stability margin coefficient,

>0 is
switching law, the Lyapunov func-
assumed.
To determine the
tion candidate with

is defined as follows:

2
1
2
Vx  
efinite function,
(22)
If the first-order derivative V of the Lyapunov func-
tion is a negative d

can converge to
0. So the control input is the sum of the linear and
non-linear inputs.
(23)
nl
eq nl
Here, non-linear input u is obtained as follows:
uu u

1
nl
uk SB



  (24)
If >0, k

>0
en
, k is the non
and it is efficit in compensating for unknown distur-
ba
-linear input switching gain
nces. To alleviate chatter in the control output of the
sliding mode controller, we used


 as the output
alteration, which is generally called the smooth function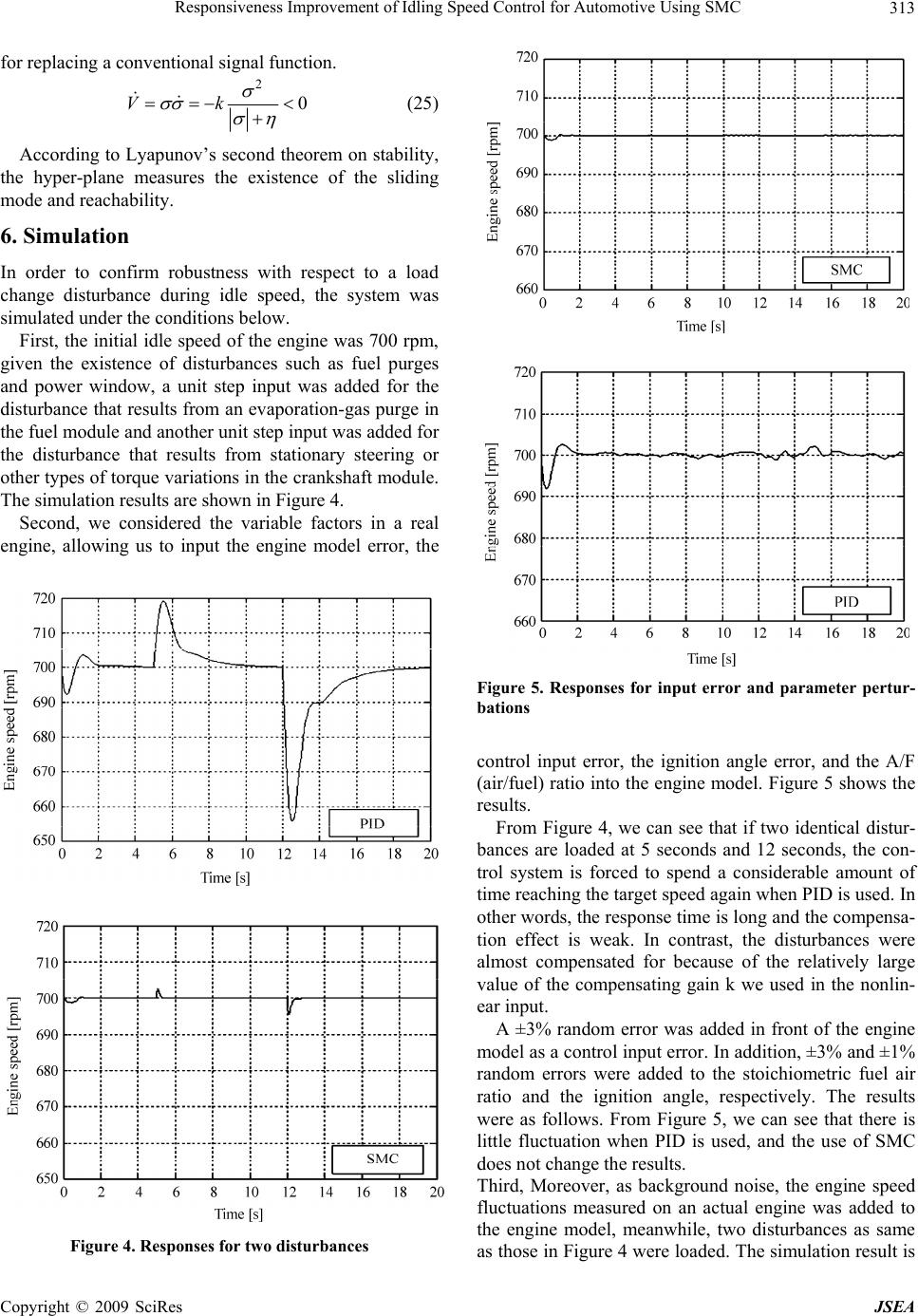

Responsiveness Improvement of Idling Speed Control for Automotive Using SMC313
for replacing a conventional signal function.
2
0Vk

   

 (25)
According to Lyapunov’s second theo
the hyper-plane measures the existence of the sliding
m a
th resp
d, th
fuel purges
and power window, a unit step input w
disturbance that results from an evaporation-gas purge in
th
e shown in Figure 4.
sidered the variable factors in a real
rem on stability,
odend reachability.
6. Simulation
In order to confirm robustness wiect to a load
change disturbance during idle speee system was
simulated under the conditions below.
First, the initial idle speed of the engine was 700 rpm,
given the existence of disturbances such as
as added for the
e fuel module and another unit step input was added for
the disturbance that results from stationary steering or
other types of torque variations in the crankshaft module.
The simulation results ar
Second, we con
engine, allowing us to input the engine model error, the
F
bations
igure 5. Responses for input error and parameter pertur-
control input error, the ignition angle error, and the A/F
(air/fuel) ratio into the engine model. Figure 5 shows the
results.
From Figure 4, we can see that if two identical distur-
bances are loaded at 5 seconds and 12 seconds, the con-
trol system is forced to spend a considerable amount of
time reaching the target speed again when PID is used. In
other words, the response time is long and the compensa-
tion effect is weak. In contrast, the disturbances were
almost compensated for because of the relatively large
value of the compensating gain k we used in the nonlin
ear input.
s a control input error. In addition, ±3% and ±1%
ndom errors were added to the stoichiometric fuel air
ctuation when PID is used, and the use of SMC
do
as those in Figure 4 were loaded. The simulation result is
-
A ±3% random error was added in front of the engine
model a
ra
ratio and the ignition angle, respectively. The results
were as follows. From Figure 5, we can see that there is
little flu
es not change the results.
Third, Moreover, as background noise, the engine speed
fluctuations measured on an actual engine was added to
the engine model, meanwhile, two disturbances as same
Figure 4. Responses for two disturbances

Responsiveness Improvement of Idling Speed Control for Automotive Using SMC 314
shown in Figure 6. The control system with the sliding
mode controller is clearly more effective against both of
the two disturbances as if background noise was loaded.
Finally, we considered the responsiveness and tracing
ability when the engine is made a sudden start from a
lo
ulation results are shown in
gi
wer idle speed to a higher speed such as 2000rpm. As
far as we know, there is usually little fuel loss in the
sudden start condition due to some of fuel drops attached
to the manifold, which sometimes leads to the undesir-
able speed down. So we assumed the sudden start oc-
curred at 6 seconds and a step disturbance as fuel loss
was load at the time. The sim
Figure 7. Apparently, the transition of the sudden start by
SMC is faster than that by PI although the disturbance is
loaded.
Based on the aforementioned simulation results, we
can see that a control system with a sliding mode con-
troller is more effective with respect to either of the two
disturbances, as well as to some errors in the actual en-
ne, proving the robustness of SMC. In addition, the
tracing ability of idle speed also appears to be improved
Figure 7. Responses for a sudden start from 700 rpm
in the work condition under the sudden start with the fue
isturbance.
7. Conclusions
In this paper we addressed the issue of idle speed control
in order to improve the stability of an engine’s idle speed
and improve its fuel economy. To achieve high stability
and robustness for the idle speed control system, the
electronic throttle (which regulates the intake air flow
when an engine is idling) was taken as the control object,
the engine was modularized by MATLAB/SIMULINK,
and given that the engine system is a typical nonlinear
system, the model was linearized at the operating point.
Using a linearized state-space model, we built a hy
perter
hich we also designed a control input for a controlled
lts, PI control was used, and in accordance
ls, the parameters of proportion and
l
d
-
-plane which is adaptive to the controlled plant, af
w
plant which is the sum of the nonlinear and linear inputs,
so the SMC is constructed in m-file. To produce com-
parative resu
with Ziegler-Nicho
integral were adjusted on the initial engine speed of 700
rpm. By using SMC, the switching hyper-plane was de-
signed based on system zeros, and the system was de-
signed as a servo system in order to achieve the target
value. Compared with conventional PI control, the stabil-
ity against disturbances was improved. Furthermore, the
Figure 6. Responses for loading engine-speed signal

Responsiveness Improvement of Idling Speed Control for Automotive Using SMC 315
[3] B. Kwak and stability controller
996.
relative robustness of SMC was confirmed when an en-
gine system was simulated under parameter perturbations
and background noise. Above all, it is much more poten-
tial to improve idle speed control and pursue low speed
of the idle speed by sliding mode control.
REFERENCES
[1] H. Ando, “Gasoline direct injection engines-present and
future,” Journal of Software Engineering and Applications,
Vol. 53, No. 9, 1999.
[2] F.-C. Hsieh and B.-C. Chen, “Adaptive Idle-speed control for
spark-ignition engines,” SAE paper: 011197, 2007.
Y. Park, “Robust vehicle
based on multiple sliding mode control,” SAE paper: 011060,
2001.
[4] Y. Zhang, T. Koorikawa and N. Kurihara, “Evaluation of
sliding mode Idle-speed control for SI engines,” Journal of
Software Engineering and Applications, Vol. 40, No. 4, pp.
997–1002, 2009.
[5] E. Hendricks, A. Chevalier and M. Jansen, et al., “Modeling
of the intake manifold filling dynamics [J],” SAE960037, pp.
1–25, 1
[6] K. Nonami and H. Tian, “Sliding mode control of
nonlinear robust control theory,” Chapter 3, Corona pub-
lisher, Tokyo, 1994.