I. J. Communications, Network and System Sciences, 2008, 3, 207-283
Published Online August 2008 in SciRes (http://www.SciRP.org/journal/ijcns/).
Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences, 2008, 3, 207-283
OCDMA/OCDMA Overloading Scheme for Cellular
DS-CDMA Using Orthogonal Gold Codes and
Complex Scrambling
Preetam KUMAR, Saswat CHAKRABARTI
G S Sanyal School of Telecommunications, IIT Kharagpur, India
Received on May 5, 2008; revised and accepted on June 27, 2008
Abstract
Overloading is a method to extend capacity limitation of multiple access techniques. The system becomes
overloaded, when the number of users exceeds the signal dimensions. One of the efficient schemes to
overload a CDMA system is to use two sets of orthogonal signal waveforms (O/O). In this paper, the BER
performance of a new overloading scheme using scrambled orthogonal Gold code (OG/OG) sets is evaluated
with soft decision interference cancellation (SDIC) receiver. When complex scrambling is not used, it is
shown that OG/OG scheme provides 25% (16 extra users) channel overloading for synchronous DS-CDMA
system in an AWGN channel, with an SNR degradation of about 0.35 dB as compared to single user bound
at a BER of 1e-5. We have evaluated the overloading performance, when two set are scrambled with set
specific deterministic or random complex scrambling sequence. It is shown that the amount of overloading
increases significantly from 25% to 63% (40 extra users) by using random complex scrambling for N=64.
For deterministic (periodic) scrambling, the overloading percentage increases considerably to 78. On a
Rayleigh fading channel, an overloading of 40% is obtained without scrambling at a BER of 5e-4 with near
single user performance. With complex scrambling overloading % increases considerably to 100%.
Keywords: DS-CDMA, Orthogonal Codes, Overloading, Interfernce Cancellation
1. Introduction
Efficient use of the available radio spectrum is an
important requirement for future wireless communication.
The number of users supported in a DS-CDMA cellular
system is typically less than spreading factor (N), and the
system is said to be underloaded. As the demand for
cellular CDMA increases, the number of users naturally
exceeds the available dimension due to bandwidth
limitation. Overloading is a technique to accommodate
more number of users than the spreading factor N. This is
an efficient scheme to increase users in a fixed bandwidth,
which is of practical interest to mobile system operators.
But the increase in capacity is obtained with a cost in
BER and receiver complexity. In fact this type of channel
overloading is provisioned in the 3G standard [1].
Among the approaches described in the literature, the
most efficient ones use multiple sets of orthogonal codes
[2]. The concept of overloading in a DS-CDMA system
using two sets of orthogonal codes is explained with the
help of Figure1. For the first N users, the system allocates
orthogonal codes drawn from the first set of N codes.
When the number of intending users exceeds ‘N’, the
excess users are accommodated in the system by
providing suitable codes drawn from a second set of M
codes. In this way, we are able to accommodate greater
number of users (K) than the spreading length N (K>N),
and the cell becomes overloaded.
The number of active users (K) in a conventional
synchronous orthogonal CDMA environment is limited
by the spreading factor N, which is WT where W is the
transmission bandwidth and T is the duration of a symbol.
When K exceeds N, the system becomes overloaded and
the signatures are no longer orthogonal. This leads to
multiple access interference (MAI). In an overloaded
system, a conventional matched filter receiver is not
optimal, due to the high level of MAI. Multiuser
detection (MUD) is required in order to obtain a

208 P. KUMAR ET AL.
Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences, 2008, 3, 207-283
satisfactory performance of the users. Linear MUDs, such
as the decorrelator, the minimum mean squared error
detector or linear decision directed interference
cancellation are devised to detect users in an underloaded
system. The Maximum Likelihood (ML) detection is not
an option because of its complexity that is exponential in
the number of users. The nonlinear MUDs such as
multistage parallel interference cancellation (PIC) and
successive interference cancellation (SIC) [3], have good
complexity- performance trade-off as compared to other
MUDs. Hence these MUDs are suitable for overloaded
systems.
It is interesting to note that several studies have been
made in the recent past to understand, analyze and
evaluate the detrimental effects of overloading. Almost
all studies consider the uplink or reverse link and several
studies suggest usage of appropriate multiuser detection
(MUD) schemes at the base station receiver. For example,
a method of accommodating K = N + M users in an N-
dimensional signal space that does not compromise the
minimum Euclidean distance of the orthogonal signaling
has been presented in [4] for AWGN channel. A tree-like
correlation coefficient structure of user signatures
suitable for optimal multiuser detection has been
proposed in [5]. In another approach, two sets of
orthogonal codes which are orthogonal within the sets is
introduced in [6]. In [6], the orthogonal sets are generated
using Walsh-Hadamard (WH) codes, where the same
WH code set is scrambled with set specific scrambling
sequence (s-O/O). An iterative multistage detection
technique has been proposed to cancel the interference
between the two sets of user. In [7], it is shown that for
uncoded BPSK modulated CDMA signal with N=64, an
overloading of 11% can be achieved in an AWGN
channel for s-O/O scheme. Another kind of receiver
simplification is presented in [8], where signals are
divided into groups that are orthogonal to each other. A
new overloading scheme using hybrid techniques has
been proposed in [9], where the spreading codes and
transmission modes are different for the two sets to
increase the overloading performance. The attractive
property of the overloading scheme was the incentive to
integrate a particular type of O/O, called quasi-
synchronous sequences (QOS) [10], into cdma2000
standard [11].
To the best of our knowledge, the usage of orthogonal
Gold codes has not been considered in any of the
overloading schemes. In [12], a new method for
generating different orthogonal sets of same length has
been proposed. The new algorithm generates (N-1)
distinct, orthogonal sets of N sequences of length N. It
has been shown that the peak value of crosscorrelation
between different sets of same length is less than half the
sequence length for
32
N
≥
. Such sequence sets would
offer low intracell interference, when used in overloaded
environment. Recently, the present authors have
proposed a new overloading scheme using a set of Gold
codes [13], which provides better performance than s-
Figure 1. Overloading scheme in a DS-CDMA cellular
system.
O/O scheme [7]. In this paper, we have evaluated the
BER performance using orthogonal Gold code (OG/OG)
sets with IMSD schemes. An efficient iterative multistage
detection with soft decision interference cancellation is
used to increase the amount of overloading.
This paper is organized as follows. In the next section,
we describe the system model for the O/O overloading
scheme. In section 3 we explain the IMSD operation and
describe the process of iterative interference cancellation.
Simulation results are presented and discussed in Section
4. Finally, we present the conclusion of this paper.
2. System Model for OCDMA/OCDMA
In the section we consider a DS-CDMA system with
processing gain N and the number of users K users
(=M+N), where M is the number of set-2 users. We
assume that the channel is a nondispersive additive white
Gaussian noise (AWGN) channel and that the different
user signals are in perfect time synchronization. The
discrete-time matrix model of the received BPSK
modulated CDMA signal after demodulation and chip
sampling may now be expressed as:
1222
= ++
121 1
r= r+rbASbASn
(1)
Here r
1
and r
2
are the received samples from set-1 and
set-2 uers respectively;
{
}
111 121
, ,.......,
N
b bb
=b and
{
}
221 222
, ,.......,
M
b bb=b represent information bits of two
sets of users, where
{
}
1
ij
b
∈ ±
.
{
}
1 111
,.......
T
T TN
=S ss is the
set of orthogonal sequences for set-1 users and is of
dimension
( )
N N
× .
{
}
2 212
,.....,
T
T TM
=S ss is another set of
orthogonal sequences for set-2 users and is of dimension
( )
M N
× . Additive noise
n
is normally distributed with
zero mean and variance equal to
2
σ
.
1
A
and
2
A
are the

OCDMA/OCDMA OVERLOADING SCHEME FOR CELLULAR DS-CDMA 209
USING ORTHOGONAL GOLD CODES AND COMPLEX SCRAMBLING
Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences, 2008, 3, 207-283
Figure 2. Block diagram of iterative multistage detection
(IMSD) for overloaded DS-CDMA scheme.
diagonal matrices of received signal amplitudes of set-1
and set-2 users respectively.
The received chip sampled and demodulated signal (1)
is despread and integrated over a bit duration to get a soft
estimate about a transmitted bit. These soft estimates are
fed to an iterative multistage detector (IMSD) (Figure 2).
As N > M set-1 users matched filter outputs are more
reliable (due to less MAI) as compared to the set-2
matched filter outputs (MAI=1). In the first iteration we
will assume
0
2
I
=0 and accordingly find
1
1
ˆ
b
and
estimate
1
1
I
. This estimated interference is removed from
the received signal, before taking decisions on set-2 users.
Subsequently we find
1
2
ˆ
b
and estimate the interference
1
2
I
on set-1 users from set-2 users. In the second iteration,
we obtain the refined data estimates of set-1 users,
2
1
ˆ
b
after removing the estimated interference
1
2
I
as shown in.
As we have more reliable data estimates of set-1 users, a
refined estimate of
2
1
I
is obtained in second iteration.
This process repeats for required number of iterations, so
that near single user performance is obtained.
When scrambling is used, the orthogonal Gold codes
of both the sets are overlaid by a set-specific pseudo-
noise (PN) sequence which is the same for all users
within the set. In other words, we have
11 2
1
[ ]
N
N
=Sα α........
α
and
21 2M
1
[ ]
N
=Sβ β........
β
.
Let
111 221
( ,,.....)
T
N
p pp= P and
212 222
( ,,.....)
T
N
p pp= P
designate the PN sequences overlaying the orthogonal
Gold sequences in the two sets of users. In order to split
the interference power evenly over the in-phase and
quadrature components of the useful signal (irrespective
of the carrier phase), we consider complex valued PN
sequences: the chips
nu
p
takes their values from the set
{ }
exp(/4), exp(3/4), exp(5/4), exp(7/4)
C
j jjj π π ππ
=
The scrambling sequence can be deterministic
(periodic) or random. In periodic scrambling, the
scrambling sequence randomly takes values form the set
C and it is kept constant for all symbols. On the other
hand, in random complex scrambling, it takes random
complex values from the set C for each transmitted
symbol.
In the next section, we explain iterative multistage
detection scheme, which reduces the high level of
interference due to overloading.
3. Iterative Multistage Detection
The received demodulated and chip sampled signal (1) is
despread and we obtain soft outputs of the transmitted
bits corrupted by multiple access interference (MAI)
from other users and AWGN noise. In conventional
matched filter detection, these outputs are fed to the
decision device to make hard decisions of the transmitted
information bits. In this paper, iterative multistage
detection (IMSD) technique is used to remove the MAI
between two sets users. The basic principle of this
receiver is to iteratively remove the estimated
interference from each set due to the users of other set in
multiple stages such that near single user performance is
achieved. The interference power from set2-user
(assuming that the useful signal power is normalized) is
1/N, and therefore the total interference power that
affects set1-users is M/N. As long as M remains small
compared to N, preliminary decisions can be made on the
symbols transmitted by set1-users with some good
reliability. But each of the set2-users gets an interference
power of N (1/N) =1 from set1-users. Clearly the bit error
(BER) performance will be poor for this set of users if
detection is made prior to interference cancellation. As
set1-users are detected with some good reliability, we can
+
+
Set-1
Matched
Filter
Output
Set-2
Matched
Filter
Output
r
-
-
1
ˆ
i
b
2
ˆ
i
b
( 1)
2i
−
I
( 1)
2i
−
I
Composite
signal of
set-1 users
Composite
signal of
set-2 users
Sequence
spreader
Sequence
spreader
1
i
y
2
i
y
Decision
Decision
1
i
I

210 P. KUMAR ET AL.
Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences, 2008, 3, 207-283
estimate the interference created from this set on set2-
users. This estimated interference is removed from set2-
uers before making the decision. Now in second iteration,
interference from set2-users on set-1 are estimated form
the first iteration outputs of set-1 and a more reliable set1
bits are obtained. This process continues till we get a near
single user performance.
To explain the operation of IMSD the following
notations are used:
1
ˆ
i
b
and
2
ˆ
i
b
are decisions about set-1
and set-2 user data bits at the
i
-th iteration;
1
i
y
and
2
i
y
are set-1 and set-2 matched filter outputs at
i
-th iteration
respectively.
At each stage of iteration, the decision on an
information bit is made according to the following
expressions:
(
)
i( -1)
111 2
ˆ
( )()
iT i
φ φ = =−bySrI (2)
(
)
2221
ˆ
( )()
iiT i
φ φ = =−
bySrI
(3)
Here the reconstructed interference for two groups in
i
-
th iteration are
1 1 1
ˆ
i i
=
1
Ib A S
and
222 2
ˆ
i i
=
IbA S
. We assume
that the reconstructed interference for the first group of
users in the first iteration is zero i.e.,
0
2
I
=0. Matched
filter outputs after interference cancellation form the
decision vectors
1
i
y
and
2
i
y
for set-1 and set-2 user data
bits respectively.
We have assumed equal power, equal phase
synchronous users in a single cell environment over an
AWGN channel. The set-1 matched filters outputs in
matrix form may be expressed as
1
1 12
()
iT(i- )
= −yS r I (4)
( 1)
1122 222 2
ˆ
( )
T i −
=++ −
i
11 1
ySb ASbA SnbAS
( 1)
1 22221
ˆ
( )
TiT −
= +−+
1
bS S AbbS n
(5)
In the case of AWGN channel, amplitude matrix is an
identity matrix, i.e.,
A=I
. For the
l
-th user of set-1,
the matched filter output during i-th iteration is
M( -1)
1,1,2, 2,,
k=1
ˆ
= +(-)+
i i
llkkl kl
ybbbz
ρ
∑
(6)
where l = 1, 2, 3………, N and
l
z
=
1
[Sn]
T
l
is the noise
sample for
l
-th user. The following notations have been
used:
1,
l
s
=
l
-th user (set-1 ) signature;
1,
l
b
=
l
-th user
transmitted data-bit (set-1 );
2,
k
b
=
k
-th user transmitted
data-bit (set-2);
( 1)
2,
ˆ
i
k
b
−
=
k
-th user tentative decision (set-
2) on
2,
k
b
at ( i- 1)
th
iteration;
,
l k
ρ
=Normalized cross-
correlation value between set-1
l
-th user and set-2
k
-th
user signatures. The matched filter output
1,
i
l
y
has three
components:
{
{
( -1)
1,1,2, 2,,
ˆ
( -)
1
-2
i i
llk klkl
Total Noise
M
ybb bz
k
Noise sample
desired MAIfrom setusers
data
ρ = + +
∑
=
144424443
14444444244444443
(7)
Considering all N set-1 users and sufficient number of
set-2 users, we assume Gaussian approximation of MAI.
So, the following expression from (7) is used to indicate
the total noise:
Total Noise =
( -1)
2, 2,,
1
ˆ
(-)
Mi
kkl kl
k
b bz
ρ
=
+
∑
(8)
In equation (2) and (3),
(
)
1,
l
b
φ is the decision
function of l -th user (set-1). According to the decision
function
(
)
1,
l
b
φ , IMSD can be classified as hard decision
interference cancellation (HDIC) or soft decision
interference cancellation (SDIC). For HDIC receiver the
decision function is defined as:
( )
1,
1, 1,1,
1 0
( )
1 0
l
l l
l
b
bsgn bb φ
− <


== 
>

 (9)
For SDIC except for the last iteration, where we take
hard decision, in other iterations several nonlinear
decision functions can be used. We have used piecewise
linear approximation of hyperbolic tangent and is defined
as:
( )
1, 1,
1, 1,
1,1,
( )
sgn()
ll
l l
l l
bb
bsgn b
b b
θ
θ
φ
θ

<

== 

≥

(10)
Here
θ
is selected to minimize the average BER.
4. Simulation Results
This section presents the Monte-Carlo simulation results
of the proposed scheme with SDIC technique. The
simulation has been carried out in MAT-LAB to evaluate
the BER performance of the proposed scheme in an
AWGN channel.
Relevant simulation parameters are shown in Table 1.
The value of the parameter
θ
is found through simulation
as 0.5 for SDIC and it is fixed for all iterations. For all
simulations, the system performance is evaluated by
means of critical overload. We define the critical overload
as the maximum achievable channel overload
(
)
max max
β
= K-N /N
with interference cancellation, so that
the SNR degradation for an average BER of 1e-5 is less
than 0.35 dB as compared to single user performance. It is
a measure for the maximum acceptable channel overload,

OCDMA/OCDMA OVERLOADING SCHEME FOR CELLULAR DS-CDMA 211
USING ORTHOGONAL GOLD CODES AND COMPLEX SCRAMBLING
Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences, 2008, 3, 207-283
Table 1. Description of some parameters relevant in
simulation.
Parameters Specifications
Transmission mode Synchronous
Modulation/ Spreading BPSK/BPSK
Sp
reading factor,
N
64
Spreading codes Orthogonal Gold codes
Power and phase
of users
Equal
Type of Receiver SDIC
Assumptions
Perfect chip, symbol and
carrier synchronization
so that the system performance is degraded slightly as
compared to the single user performance.
To increase the amount of overloading an efficient soft
decision interference cancellation receiver is used as
described in Section 3. In Figure 3, BER performance of
this receiver at different overloading has been shown for
N=64 at 28%, 25% and 22% overloadings. It is observed
that 28% overloading cannot be achieved, with less than
1.0 dB SNR degradation at an average BER of 1e-5. If we
reduce the overloading to 25%, the SNR degradation is
about 0.35 dB as shown in Figure 3 and we can ensure a
BER of
5
10
−
for all users. So, we can obtain a critical
overload of 25%, when the spreading factor N is 64. We
have observed that the amount of critical load is only 19%,
when the spreading length is reduced to 32.
The critical channel overload for s-O/O is 3% and 11%
for N=32 and 64 respectively [7] for the same set of
parameters. So there is a significant improvement in
critical channel overload in OG/OG scheme as compared
to s-O/O scheme.
In Figure 4, the BER performance of OG/OG scheme
with random complex scrambling is shown for N=32.
Here, both the sets are scrambled by a set specific
complex random scrambling sequence. We observe from
the figure that, with complex scrambling the amount of
overloading is 31%, with about 0.35 dB SNR degradation
as compared to single user performance. In Figure 5,
overloading performance with periodic scrambling is
shown. It is interesting to observe that the overloading
performance increases to 50% with less than 0.35 dB SNR
degradation.
In Figure 6, the BER performance with complex
random scrambling is shown for N=64. Here we observe
that we can support 40 extra users (63% channel
overloading), with less than 0.35 dB SNR degradation as
compared to single user bound. In Figure 7, BER
performance with periodic complex scrambling is shown.
It is shown that with periodic scrambling, critical load
increases to 78%. This is a significant amount of channel
overloading, which can be obtained with complex
scrambling. Hence, complex scrambling increases the
amount of overloading significantly in an overloaded DS-
CDMA system as compared to unscrambled OG/OG
scheme [13].
5. BER Performance on a Rayleigh Fading
Channel
We notice that the case of an AWGN channel is obtained
by taking the received signal amplitude matrix,
k
A = I
.
The Rayleigh fading channel model can be described by
fading amplitudes generated according to
(
)
(
)
j
I Q
k kk
a aa
= + , where
(
)
I
k
a
and
(
)
Q
k
a
are independent
zero-mean real Gaussian distributed random variables
with variance
( )()
2 2
1/2
I Q
k k
a a
σ σ = = .
In order to compare the performance of these schemes,
we define the critical overload as the maximum
achievable channel overload
(
)
max maxmax
β
=/K-N /N
MN =
with interference cancellation receiver, so that the SNR
degradation as compared to a single user system at an
average BER of 5e-4 is less than 1 dB in an AWGN
channel. It has to be emphasized that the receiver does
not require any kind of user sorting to yield the desired
overloading performance. As a consequence, this
measure guarantees that the mean BER performance
remains close to that of the ideal BER curve provided
that
max
M M < . It is worth noting that the BER
performance in case of perfect interference cancellation is
identical to the performance of a non-overloaded system
where the users are orthogonal, and also to the
performance of a single-user system. The BER achieved
by a single-user transmitting over a Rayleigh fading
channel is given by
0
1 1
1
21 /
b
e
b
P
N E
 
= −
 
 
+
 
(11)
In Figure 8, the BER performance of OG/OG scheme
with conventional matched filter and SDIC receiver on a
Rayleigh fading channel is shown. We have considered
set 1 and set 6 users for simulation. Figure 7 also shows
the theoretical single-user BER performance over a
Rayleigh fading channel. The channel overloading is fixed
at 40% (26 extra users). It can be observed that the SNR
degaradation at a BER of
4
5.10
−
is about 1 dB. So, we
can obatain 40% channel overloading on a Rayleigh
fading channel with the SDIC receiver for N = 64.
Figure 9 shows the BER performance of scrambled
OG/OG scheme, where a single set of orthogonal Gold
code is used. The amount of overloading is fixed at 100%
for N = 64. It is interesting to observe that the
overloading increases considerably from 40% to 100%
(64 extra users). The overloading for s-O/O [6] scheme is
only 75% with complex scrambling with same set of
simulation parameters. When we choose two different
sets of orthogonal codes and complex scrambling, the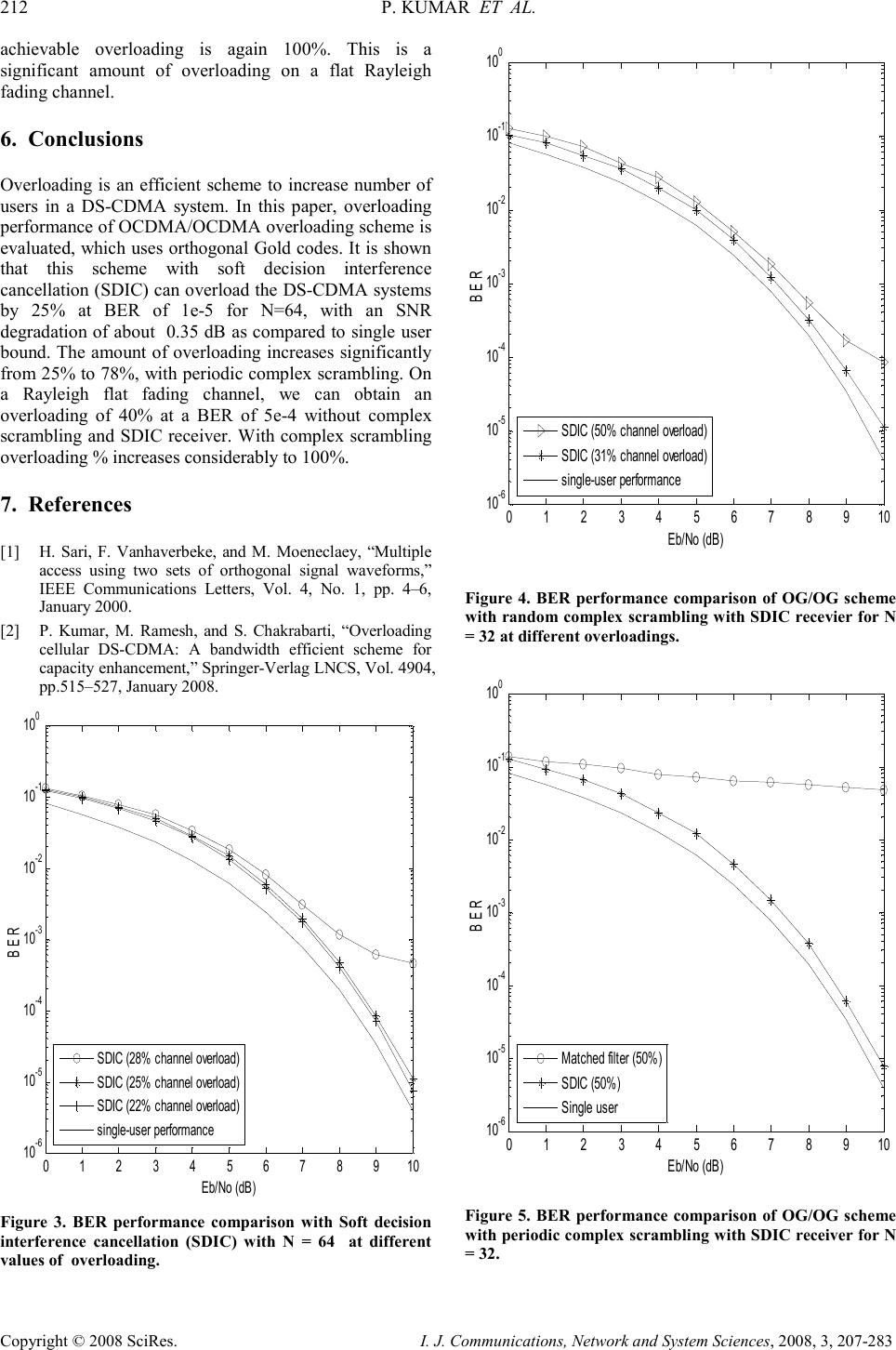

212 P. KUMAR ET AL.
Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences, 2008, 3, 207-283
achievable overloading is again 100%. This is a
significant amount of overloading on a flat Rayleigh
fading channel.
6. Conclusions
Overloading is an efficient scheme to increase number of
users in a DS-CDMA system. In this paper, overloading
performance of OCDMA/OCDMA overloading scheme is
evaluated, which uses orthogonal Gold codes. It is shown
that this scheme with soft decision interference
cancellation (SDIC) can overload the DS-CDMA systems
by 25% at BER of 1e-5 for N=64, with an SNR
degradation of about 0.35 dB as compared to single user
bound. The amount of overloading increases significantly
from 25% to 78%, with periodic complex scrambling. On
a Rayleigh flat fading channel, we can obtain an
overloading of 40% at a BER of 5e-4 without complex
scrambling and SDIC receiver. With complex scrambling
overloading % increases considerably to 100%.
7. References
[1] H. Sari, F. Vanhaverbeke, and M. Moeneclaey, “Multiple
access using two sets of orthogonal signal waveforms,”
IEEE Communications Letters, Vol. 4, No. 1, pp. 4–6,
January 2000.
[2] P. Kumar, M. Ramesh, and S. Chakrabarti, “Overloading
cellular DS-CDMA: A bandwidth efficient scheme for
capacity enhancement,” Springer-Verlag LNCS, Vol. 4904,
pp.515–527, January 2008.
0 1 2345 6 78910
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
Eb/No (dB)
BER
SDIC (28% channel overload)
SDIC (25% channel overload)
SDIC (22% channel overload)
single-user performance
Figure 3. BER performance comparison with Soft decision
interference cancellation (SDIC) with N = 64 at different
values of overloading.
0 1 23 45 6 78 910
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
Eb/No (dB)
BER
SDIC (50% channel overload)
SDIC (31% channel overload)
single-user performance
Figure 4. BER performance comparison of OG/OG scheme
with random complex scrambling with SDIC recevier for N
= 32 at different overloadings.
0 123 45 6 78 910
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
Eb/No (dB)
B E R
Matched filter (50%)
SDIC (50%)
Single user
Figure 5. BER performance comparison of OG/OG scheme
with periodic complex scrambling with SDIC receiver for N
= 32.

OCDMA/OCDMA OVERLOADING SCHEME FOR CELLULAR DS-CDMA 213
USING ORTHOGONAL GOLD CODES AND COMPLEX SCRAMBLING
Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences, 2008, 3, 207-283
0 1 23 45 6 78 910
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
Eb/No (dB)
BER
SDIC (63% channel overload)
SDIC (50% channel overload)
single-user performance
Figure 6. BER performance comparison of OG/OG scheme
with random complex scrambling with Soft decision
Interference cancellation (SDIC) for N = 64.
0 1 23 45 678 910
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
Eb/No (dB)
B E R
SDIC (83% overload)
SDIC (78% overload)
single-user performance
Figure 7. BER performance comparison of OG/OG scheme
with periodic complex scrambling with Soft decision
Interference cancellation (SDIC) for N = 64.
0510 15 20 2530
10
-4
10
-3
10
-2
10
-1
10
0
Eb/No (dB)
BER
conventional receiver
SDIC ( channel overload 40%)
single user performance
Figure 8. Mean BER performance of OG/OG with 40%
overload and SDIC receiver over a Rayleigh fading channel
without scrambling.
051015 20 2530
10
-4
10
-3
10
-2
10
-1
10
0
Eb/No (dB)
B E R
Matched filter (100%)
SDIC (100%)
Single user performance
Figure 9. BER performance of s-OG/OG scheme with 100%
overloading with random complex scrambling over a
Rayleigh fading channel for N = 64.

214 P. KUMAR ET AL.
Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences, 2008, 3, 207-283
[3] S. Verdu, “Multi–user detection,” Cambridge University
Press, 1998.
[4] J. A. F. Ross and D. P. Taylor, “Vector assignment scheme
for M+N users in N-dimensional global additive channel,”
Electronics Letters, Vol. 28, August 1992.
[5] R. E. Learned, A. S. Willisky, and D. M. Boroson, “Low
complexity joint detection for oversaturated multiple
access communications,” IEEE Transactions Signal
Processing, Vol. 45, pp. 113–122, January 1997.
[6] F. Vanhaverbeke, M. Moeneclaey, and H. Sari,
“DS/CDMA with two sets of orthogonal sequences and
iterative - detection,” IEEE Communications Letters, Vol.
4, pp. 289–291, September 2000.
[7] F. Vanhaverbeke and M. Moeneclaey, “Critical load of
oversaturated systems with multistage successive
interference cancellation,” IEEE VTC, Vol. 4, pp. 2663–
2666, April 2003.
[8] D. Djonin and V. K. Bhargava, “New results on low
complexity detectors for oversaturated CDMA systems,”
in Proceedings of Globecom 2001, pp. 846–850,
November 2001.
[9] P. Kumar and S. Chakrabarti, “A new overloading scheme
for DS-CDMA system,” National Conference on
Communication, IIT Kanpur, pp. 285–288, 26–28 January
2007.
[10] K. Yang, Y. K. Kim, and P. V. Kumar, “Quasi-orthogonal
sequences for code-division multiple-access systems,”
IEEE Transactions on Information Theory, Vol. 46, pp.
982–993, May 2000.
[11] Physical Layer Standard for cdma2000 Spread Spectrum
Systems, Realse B, TIA/EIA 3GPP2 C.S0002-B, January
16, 2001.
[12] H. Donelen and T. O. Farrell, “Methods for generating sets
of orthogonal sequences,” Electronics Letters, Vol. 35, pp.
1537–1538, September 1999.
[13] P. Kumar and S. Chakrabarti, “A new overloading scheme
for cellular DS-CDMA using orthogonal gold codes,”
IEEE Vehicular Technology Conference (VTC), pp. 1042–
1046, May 2008.