Paper Menu >>
Journal Menu >>
 Int. J. Communications, Network and System Sciences, 2009, 2, 912-916 doi:10.4236/ijcns.2009.29106 Published Online December 2009 (http://www.SciRP.org/journal/ijcns/). Copyright © 2009 SciRes. IJCNS A New Multicast Wavelength Assignment Algorithm in Wavelength-Converted Optical Networks Anping WANG, Qiwu WU, Xianwei ZHOU, Jianping WANG Department of Communication Engineering, School of Information Engineering, University of Science and Technology Beijing, Beijing, China E-mail: wuqiwu700@163.com Received September 14, 2009; revised October 25, 2009; accepted November 23, 2009 Abstract In this paper, we propose a new multicast wavelength assignment algorithm called NGWA with complexity of O(N), where N is the number of nodes on a multicast tree. The whole procedure of NGWA algorithm is separated into two phases: the partial wavelength assignment phase and the complete wavelength assignment phase. It tries to minimize the total number of wavelength conversions of the multicast tree. Meanwhile, the number of different wavelengths used is minimized locally. Through illustrative example and simulation ex- periments, it is proved that the NGWA algorithm works well and achieves satisfactory performance in terms of the average number of wavelength conversions and the average blocking probability. Keywords: WDM Network, Multicast, Wavelength Assignment, Wavelength Conversion 1. Introduction Multicast is an efficient way to implement one-to-many communication. The problem of finding a multicast tree and allocating available wavelength for each link of the tree is known as the Multicast Routing and Wavelength Assignment (MC-RWA) problem, which plays a key role in supporting multicasting over WDM networks [1]. Since improper wavelength assignment will cause low network capacity and high connecting blocking probabil- ity, the problem of how to assign wavelengths for the multicast tree becomes an important problem in a WDM optical network. According to the different number of multicast connecting requests, the multicast wavelength assignment (MC-WA) problem can be divided into two categories: MC-WA for single multicast which was stud- ied in [2–5] and MC-WA for multiple multicasts which was studied in [6–8]. But to our best knowledge, few studies have been done on the multicast wavelength as- signment (MC-WA) problem to minimize both the total number of wavelength conversions of the multicast tree and the number of different wavelengths used. Based on the above, we will propose a greedy algorithm to solve the MC-WA problem. The rest of the paper is organized as follows. Section 2 introduces the network model and the problem specifica- tion. Section 3 proposes a new multicast wavelength as- signment algorithm, and an illustrative example is given. The simulation results are shown in Section 4. Finally, the paper is concluded in Section 5. 2. Problem Formulation 2.1. Network Model The assumptions for the MC-WA problem in this paper are given as follows: 1) The WDM network is an arbitrary connected graph. 2) All links in the network are equipped with the same set of wavelengths. 3) All nodes are provided with full wavelength con- version capacity and light splitting capacity. Let a directed graph G=(V, E, M) is used to represent a WDM network where V is the vertex set with |V|=n, E represents the set of links and M={λ1, λ2,…λk,} is the set of wavelengths supported by each link with |M|=k. Meanwhile, let () MeM ⊂ be the set of available wave- lengths on link e. In the graph G=(V, E, M), each vertex node v∈V or each edge e∈E is associated with the following costs: Wavelength usage cost, C w (e, λ i ), the cost of using wavelength λi on link e, which is used to computer the multicast tree in multicast routing algorithm. Wavelength conversion cost, C c (v, λ p , λ q ), the wave- length conversion cost from input wavelength λp to out- put wavelength λq at node v, and if λp=λq, then Cc(v, λ p ,  A. P. WANG ET AL. Copyright © 2009 SciRes. IJCNS 913 λq)=0. Otherwise, if either λp or λq is not available, then Cc(v, λp, λq)=∞. Note that the wavelength conversion cost between any two different available wavelengths is the same in this paper, i.e., Cc(v, λp, λq)=1. Hence, it’s obvi- ous that the total cost of wavelength conversions can be reduced to the number of wavelength conversions. Let r(s:D) be a multicast request, where s is the source node and D is the set of all destination nodes. And the route from the source to each of the destinations is rep- resented to be a multicast tree T(VT, ET). In the tree T, let ev be the input link of node v, A(e v ) be the available wavelength set on the input link of node v excepting the rout node, Out(v) be the set of output links of node, and Q(v) be the set of child nodes of node v. Given a multicast tree T and the available wavelength set A(ev) of all links in the tree, a wavelength assignment of T is defined as a function F:E a M, such that, for each ev∈ET, F(ev)∈A(ev). Therefore, the multicast wavelength assignment is used to assign one appropriate wavelength F(ev)∈A(ev) on each link of the tree. For each non-root node v in the tree T, we define a cost function Cc(Tv ,λ) to be the number of wavelength conversions needed in the sub-tree rooted at v, assuming wavelength λ is assigned on the input link of node v. For each leaf node v, we set Cc(Tv ,λ)=0. Hence, the total number of wavelength conversions of the tree can be defined as follows: () ()(), () Tv vQs CFCAv λλ ∈ =∈ ∑ (1) 2.2. Problem Specification Based on the above, the MC-WA problem in this paper can be described as follows: given a multicast tree T(VT, ET) rooted at node s and available wavelength set A(ev) on the input link of each non-root node v, the multicast wavelength assignment problem is to assign the wave- length set F(ev)∈A(ev) on the input link for each non- root node of the tree, while the total number of wave- length conversions for the tree T, CT (F), is minimized. Based on Equation (1), the MC-WA problem can be for- mulated as follows: () Min ()Min(), () Tv vQs CFCAv λλ ∈ =∈ ∑ (2) According to Equation (2), we can find that the total number of wavelength conversions of the tree T is the summation of the number of wavelength conversions of sub-trees that rooted at each child node of the root node. 3. The Proposed Algorithm 3.1. The NGWA Algorithm In this subsection, we will propose a new multicast wavelength assignment algorithm called NGWA. The objective of the algorithm aims to minimize the total Table 1. Parameter and definition. Parameter Definition T Multicast tree r(s:D) Multicast request, where s is the source and D is the set of all destination nodes ev Input link of node v Out(v) Set of output links of node Q(v) Set of child nodes of node v A(ev) Set of available wavelengths on the input link of node v H(ev) Candidate wavelength(s) on ev in the tree F(ev) Assigned wavelength on the input link of node v in the tree MU(λi) Counter of assigned wavelength λi Pare(v) Parent node of the node v Cc(Tv ,λ) Number of wavelength conversions needed in the sub-tree rooted at v CT (F) Total number of wavelength conversions for the tree T number of wavelength conversions of the multicast tree as few as possible; meanwhile, the number of different wavelengths used is minimized locally. The main pa- rameters in our proposed algorithm are given in Table 1. The basic steps of the NGWA algorithm are given below. Input: Multicast tree T and available wavelength set A(v) Output: Wavelength assignment for the multicast tree T. Begin Let the N nodes of T have a topological order 0, 1,…, N-1, beginning from the root node. //Partial wavelength assignment phase: For (i=1 up to N-1) Do i vv = . If node v is not a leaf node, Then Computer the candidate wavelength(s): 12|()| ()()()(), vQv HeAvAvAv ′′′ =∩∩∩ K where () i vQv ′ ∈ . If ()2 v He ≥ Then Save the set () v He and the node v is marked as “uncompleted” Else ()() vv FeHe = , (())(())1 vv MUFeMUFe =+ , the node v is marked as “completed” Endif Else If state of Pare(v) is already marked as “com- pleted” and |()|1 v Ae = Then ()() vv FeAe = . Endif Endif Endfor // Complete wavelength assignment phase:  A. P. WANG ET AL. Copyright © 2009 SciRes. IJCNS 914 For (i= N-1 up to 1) Do i vv = . If state of node v is already marked as “uncom- pleted” Then (), v Fe λ ′ = where (), v He λ ′ ∈ and () MU λ ′ is maximum among all wavelengths cur- rently. (())(())1 vv MUFeMUFe =+ . Endif Endfor End The whole procedure of the NGWA algorithm is sepa- rated into two phases: the partial wavelength assignment phase and the complete wavelength assignment phase. They are depicted as follows, respectively. 1) In the partial wavelength assignment phase, the local optimality strategy is used to computer the set of candidate wavelengths on ev which is available on the maximum number of output links. If there are more than two candi- date wavelengths, the corresponding node v is marked as “uncompleted.” Otherwise, it assigns the only wavelength on ev. Meanwhile, the node v is marked as “completed” and the counter of the corresponding wavelength increases by one. For each leaf node v∈D if the wavelength of input link of parent node of the leaf node v is assigned and the number of available wavelength on ev is only one, then the only available wavelength is assigned to link ev. 2) In the complete wavelength assignment phase, the main task is to deal with the nodes that are marked as “uncompleted” according to the order of bottom-up in the tree. Similar to the method of Most-Used [9], it chooses the wavelength that is the most-used in the multicast tree from the candidate wavelengths so as to make full use of the overall wavelength utilization situation on the tree and reduce the number of different wavelengths used. Theorem 1: The time complexity of NGWA algo- rithm is no more than O(N), where N=|VT|. Proof: The time complexity is obvious. In the first phase, the time of spanning all non-root nodes in the tree is O(N-1), where N=|VT|. In the second phase, the time complexity is same as the first phase. Therefore, the time complexity of NGWA algorithm is no more than O(N), where N=|VT|. 3.2. Illustrative Example To help further illustrate how the NGWA algorithm works, a multicast tree is given in Figure 1(a). Figures 1(b) and 1(c) depict the two phase’s executive results of the NGWA algorithm, respectively. It’s clear that the fre- quency of each wavelength λi(i=1,2,3,4) used in the tree is 2, 9, 1, and 0, respectively. And the total number of wavelength conversions is 4. 4. Simulation Results We carry out a simulation study to see how well the proposed algorithm works, and compare the performance Figure 1. The illustrative examples of (a). A given multicast tree (b). The result of the first phase (c). The result of the second phase. of our proposed NGWA algorithm to the old greedy al- gorithm proposed in [2] in terms of the average number of wavelength conversions and the average blocking probability. In view of briefness, the old greedy wave- length assignment algorithm is abbreviated to OGWA. 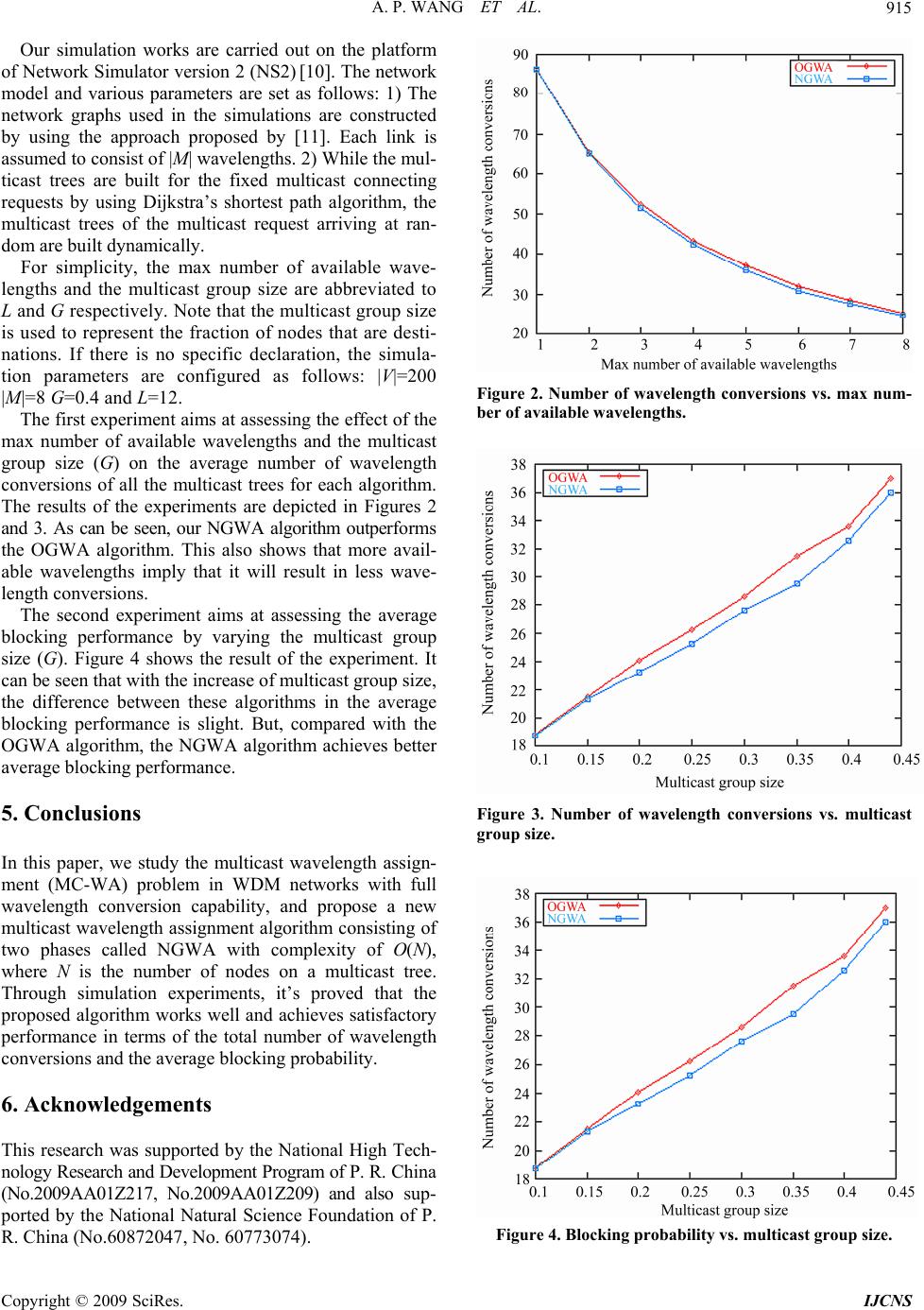 A. P. WANG ET AL. Copyright © 2009 SciRes. IJCNS 915 Our simulation works are carried out on the platform of Network Simulator version 2 (NS2) [10]. The network model and various parameters are set as follows: 1) The network graphs used in the simulations are constructed by using the approach proposed by [11]. Each link is assumed to consist of |M| wavelengths. 2) While the mul- ticast trees are built for the fixed multicast connecting requests by using Dijkstra’s shortest path algorithm, the multicast trees of the multicast request arriving at ran- dom are built dynamically. For simplicity, the max number of available wave- lengths and the multicast group size are abbreviated to L and G respectively. Note that the multicast group size is used to represent the fraction of nodes that are desti- nations. If there is no specific declaration, the simula- tion parameters are configured as follows: |V|=200 |M|=8 G=0.4 and L=12. The first experiment aims at assessing the effect of the max number of available wavelengths and the multicast group size (G) on the average number of wavelength conversions of all the multicast trees for each algorithm. The results of the experiments are depicted in Figures 2 and 3. As can be seen, our NGWA algorithm outperforms the OGWA algorithm. This also shows that more avail- able wavelengths imply that it will result in less wave- length conversions. The second experiment aims at assessing the average blocking performance by varying the multicast group size (G). Figure 4 shows the result of the experiment. It can be seen that with the increase of multicast group size, the difference between these algorithms in the average blocking performance is slight. But, compared with the OGWA algorithm, the NGWA algorithm achieves better average blocking performance. 5. Conclusions In this paper, we study the multicast wavelength assign- ment (MC-WA) problem in WDM networks with full wavelength conversion capability, and propose a new multicast wavelength assignment algorithm consisting of two phases called NGWA with complexity of O(N), where N is the number of nodes on a multicast tree. Through simulation experiments, it’s proved that the proposed algorithm works well and achieves satisfactory performance in terms of the total number of wavelength conversions and the average blocking probability. 6. Acknowledgements This research was supported by the National High Tech- nology Research and Development Program of P. R. China (No.2009AA01Z217, No.2009AA01Z209) and also sup- ported by the National Natural Science Foundation of P. R. China (No.60872047, No. 60773074). Figure 2. Number of wavelength conversions vs. max num- ber of available wavelengths. Figure 3. Number of wavelength conversions vs. multicast group size. Figure 4. Blocking probability vs. multicast group size.  A. P. WANG ET AL. Copyright © 2009 SciRes. IJCNS 916 7. References [1] Y. Z. Zhou and G. S. Poo, “Optical multicast over wave- length-routed WDM network: A survey,” Optical Switching and Networking, Vol. 2, No. 3, pp. 176–197, November 2005. [2] B. Chen and J. Wang, “Efficient routing and wavelength assignment for multicast in WDM networks,” IEEE Journal of Selected Areas Communication, Vol. 20, No. 1, pp. 97– 109, January 2002. [3] G. S. Poo and Y. Zhou, “A new multicast wavelength assignment algorithm in wavelength-routed WDM net- works,” IEEE Journal of Selected Areas Communication, Vol. 24, No. 4, January 2006. [4] R. Libeskind-Hadas and R. Melhem, “Multicast routing and wavelength assignment in multi-hop optical net- works,” IEEE/ACM Transactions on Networking, Vol. 10, No. 5, October 2002. [5] J. Wang, B. Chen, and R. N. Uma, “Dynamic wavelength assignment for multicast in all-optical WDM networks to maximize the network capacity,” IEEE Journal of Selected Areas Communication, Vol. 21, No. 8, pp. 1274–1284, October 2003. [6] X. H. Jia, D. Z. Du, X. D. Hu, et al., “Optimization of wave- length assignment for QoS multicast in WDM networks,” In Proceedings of IEEE Transactions on Communication, Vol. 49, No. 2, pp. 341–350, February 2001. [7] I. S. Hwang, S. N. Lee, and Y. F. Chuang, “Multicast wave- length assignment with sparse wavelength converters to maximize the network capacity using ILP formulation in WDM mesh networks,” Photonic Network Communica- tion, Vol. 12, No. 2, pp. 161–172, August 2006. [8] Y. W. Chen, and I. H. Peng, “Study of multicast wave- length arrangement for maximizing network capacity in WDM networks with sparse wavelength converters,” Photo- nic Network Communication, Vol. 15, No. 2, pp. 141– 152, April 2008. [9] M. Saad and Z. Luo, “On the routing and wavelength as- signment in multi-fiber WDM networks,” IEEE Journal of Selected Areas Communication, Vol. 22, No. 9, pp. 1708– 1717, June 2004. [10] The Network Simulator version 2, http://www.isi.edu/nsnam/ns/. [11] B. M. Waxman, “Routing of multipoint connections,” IEEE Journal of Selected Areas Communication, Vol. 6, No. 9, pp. 1617–1622, December 1988. |

